Задача о кручении цилиндрического тела с учетом разупрочнения

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2019PNRPU MECHANICS BULLETIN

В настоящее время при расчетах конструкций за критическое состояние принимается состояние, при котором напряжения достигают предела текучести либо предела прочности материала [1, 2]. Стадия разупрочнения (закритическая стадия деформирования) начинается после достижения материалом максимальных в данных условиях напряжений (предела прочности) и характеризуется снижением уровня напряжений при растущих деформациях [3–10]. Закритическая стадия деформирования может развиваться при равновесном накоплении повреждений и может быть устойчивой при достаточной жесткости нагружающей системы [11–13]. Экспериментально полная диаграмма деформирования материала может быть получена с использованием специальных установок [14–20]. Анализ деформируемых систем с учетом разупрочнения материала позволяет выявить условия устойчивого закритического деформирования в локальных зонах и оценить соответствующие резервы несущей способности конструкций, что показано в работах [21–27].

Аналитические решения задач с учетом полной диаграммы деформирования были получены в работах В.А. Ибрагимова, В.Д. Клюшникова (задачи чистого изгиба балки и сферической полости в пространстве, нагруженной равномерно распределенным давлением) [22]; Л.В. Никитина, Е.И. Рыжака (задача о всестороннем сжатии горных пород) [23]; С.Д. Волкова, Г.И. Дубровиной, Ю.П. Соковнина (задача растяжения пласти- ны с поперечной трещиной) [24]; В.В. Стружанова (задача о разрушении диска с ослабленной центральной зоной) [25]; В.Э. Вильдемана (задачи трехточечного изгиба балки, разрушения толстостенного цилиндра под действием внутреннего давления, задачи механики за-критического деформирования стержневых систем) [1, 26, 12].

В работе рассматривается задача кручения стержня круглого поперечного сечения при его «жестком» нагружении с учетом разупрочнения материала.

1.    Кручение стержня из упругого материала с разупрочнением

Закон связи напряжений и деформаций выбирается для простоты кусочно-линейным:

GY,               0 ^ Y ^ Y т, т = <т т - dg (Y - Y т), Y т < Y ^ Y р,

[ 0,                    Y р <  Y^.

Приведенные соотношения обеспечивают проиллюстрированную на рис. 1 двухзвенную кусочно-линейную аппроксимацию полной диаграммы деформирования: G – модуль сдвига; D_G – модуль разупрочнения при сдвиге, D_g = tge; т _т, y _т — предел текучести при сдвиге и соответствующий угол сдвига; γ _р – деформация полного разрушения. Иначе связь напряжений и деформаций на участке разупрочнения представима в виде [28]

т = GY ( 1 ^- to ( у ) ) ,

где использованы соотношения

где to (у) - функция пластичности Ильюшина [29]. Для данной задачи to (у )= X f 1 - ут ), V Y )

где

- G + D X =-----—

G

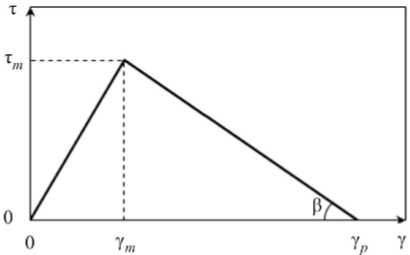
Рис. 1. Диаграмма деформирования материала с участком разупрочнения

Fig. 1. The material’s deformation diagram with weakening stage

Предполагается выполнение гипотезы плоских сечений. Относительный угол сдвига γ связан с относительным углом закручивания θ формулой [30]

Y = Op,

где ρ – расстояние от центра до рассматриваемой точки сечения; относительный угол закручивания определяется отношением угла закручивания к длине, на которой он измеряется:

9 =^ф.                          (6)

Выполнение соотношения (5) можно обеспечить при кручении цилиндрических образцов с утолщенной зоной для захватов, которая работает упруго и обеспечивает линейную связь между сдвиговыми деформациями и расстоянием от центра, на котором эти деформации рассматриваются.

Связь между внешним крутящим моментом М и относительным углом закручивания устанавливается из равенства внешних и внутренних силовых факторов с учетом (2):

R

M = J 2np² т ( p ) d p =

= 2n G 9 J p³ d p + 2n G 9 J p³ ( 1 - to ( p ) ) d p,       (7)

0                    ρ _т

	Y т   Y т	у р   у р
	---, --- < R ,	,       <  R ,
	9     9	θθ
p т =‘	p р =1	(8)
	γ R ,   ^т >  R ,	R ,    ^р >  R .
	9	,      9

Здесь ρ _т , ρ _р – расстояния от центра сечения до границ упругой зоны и зоны закритической деформации соответственно; R - радиус стержня; p _т = R при отсутствии пластических деформаций (максимальный угол сдвига меньше угла сдвига у _т ), аналогично p р = R , когда отсутствуют участки разрушенного материала. В области p р <  p <  R в случае устойчивого деформирования имеет место полностью разрушенный материал с нулевым сопротивлением внешним нагрузкам.

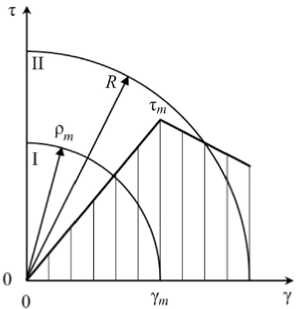
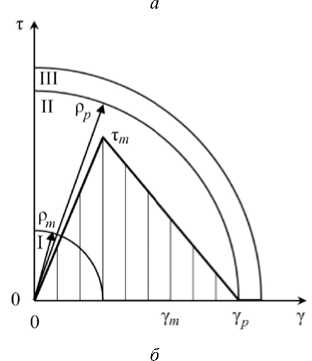
Рис. 2. Эпюры распределения напряжений: a – стадия начальной закритической деформации; б – стадия закритической деформации и разрушения; I – упругая зона; II – зона закритического деформирования; III – зона с разрушенным материалом; ρ _т , ρ _р – радиусы упругой зоны и зоны с разрушенным материалом соответственно определяются соотношением (8)

Fig. 2. Stress distribution diagrams: a – stage of initial supercritical deformation; b – stage of supercritical deformation and fracture; I – elastic zone; II – supercritical deformation zone; III – fractured material zone

1. Стадия начальной закритической деформации.

Данная стадия характеризуется тем, что у т <  6 R <  У р ,

γ а значит, р = —, р = R . Пусть начало закритической тθр стадии деформирования стержня с полярным моментом инерции Iρ происходит при крутящем моменте Mт

и относительном угле закручивания θ _т :

Формула (11) отражает зависимость соответствующего моменту M ^* значения экстремального относительного угла поворота сечения θ^* от λ . Данная зависимость показана на рис. 4. Из графика видно, что с уменьшением λ растет экстремальное значение θ^* . При X ^ 1: 6 * ^ ^ , материал в данном сечении переходит в пластическое состояние; радиус упругой области стремится к нулю.

θ

т

M т

GI ^ρ

Тогда, подставляя (3)–(5) в (7), получим

М м = —

θ

3 ( 1 - X ) — + X θ

θ3

θ3

Найдем точку экстремума 6* функции м (6) из условия равенства нулю производной е'=6 - 4Ц;                (11)

γ отметим, что 68 < 6р = — . Экстремальное значение крутящего момента м" = М' (^ - ^^ (^ - 1)3).             (12)

Будем понимать под резервом несущей способности величину, показывающую, насколько максимальный крутящий момент M ^* , рассчитанный с учетом участка разупрочнения материала, превышает момент M _т , рассчитанный для стержня, работающего в упругой области. Тогда формула (12) позволяет выявить и оценить резерв несущей способности с учетом неупругого деформирования. Чем меньше λ , т.е. чем меньше модуль спада системы, тем больше резерв стержня. Графически зависимость (12) показана на рис. 3.

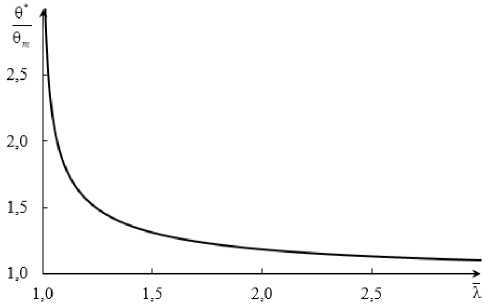
Рис. 4. Зависимость экстремального относительного угла закручивания от λ (в относительных координатах)

Fig. 4. Dependence of the extreme relative angle of rotation on λ (in relative coordinates)

2. Стадия закритической деформации и разруше ния. На данной стадии у < 6R, р„ = —, р = —-. Вы-рт           р

разим γ _р , приравняв выражение (2) нулю:

у р =      — - .                    (13)

X — 1

Тогда из выражения (7) получим

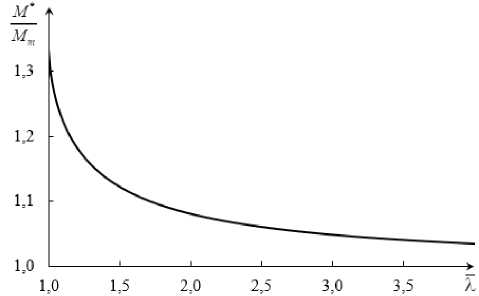
Рис. 3. Зависимость максимального значения крутящего момента от λ (в относительных координатах)

М 6³ (               ( X ⁴      1-1 X ³      ]]

м = ^^I 3 + 3 ( 1 - X )|| -— I - 1 1 + 4X II ---- I - 1 11 . (14)

3 6 3 (             (I X - 1 J J Ik X - 1 )     ))

Fig. 3. Dependence of the maximum torque value on λ (in relative coordinates)

Графики, отображающие зависимость крутящего момента от относительного угла поворота сечения, показаны на рис. 5. При «мягком» нагружении экстремальные значения являются предельными, так как невозможно дальнейшее увеличение нагрузки; при «жестком» нагружении после достижения экстремума момент может уменьшаться, асимпотически стремясь к нулю. Из графиков видно, что с увеличением λ уменьшается предельное значение крутящего момента и предельное значение относительного угла поворота. Соответственно, материал, обладающий меньшим значением коэффициента разупрочнения при сдвиге D_G , является более эффективным для применения в конструкциях, работающих на кручение.

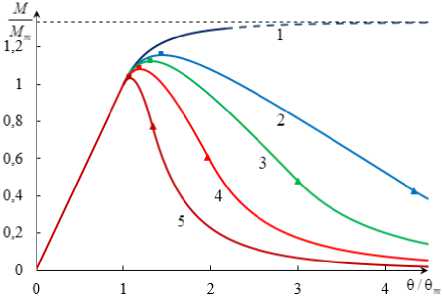
Рис. 5. Графики зависимости крутящего момента от относительного угла поворота сечения для разных значений X : 1-5 - графики для X = 1; 1,3; 1,5; 2; 4 соответственно; пунктирная линия ограничивает график для X = 1. Маркеры означают (слева направо): момент начала разупрочнения; экстремумы; момент начала разрушения материала

Из условия равенства между внутренними и внешними силовыми факторами следует равенство

M = J 2np²т ( p ) d p = 2n G 9 J p³ d p + 2п ( т _т - G 'y _т ) J p 2 d P + 00   ρ _т

+ 2n G '9 J p³ d p + 2п ( т _В + D G y _B ) J p² d p -2n D_G 9 J p³ d p. (16) ρ _т                                  ρ _B ρ _B

При записи последнего следующие обозначения:

соотношения использованы

γ _т

p т = 1

θ,

γ _т

V <  R ,

R ,

^{Y t} >  R , θ^,

Fig. 5. The dependence of torque on the relative angle of rotation of the cross section for different values of λ : 1–5 – are dependences for X = 1; 1,3; 1,5; 2; 4 respectively; the dashed line limits dependence for X = 1 . Markers mean (from left to right): the beginning of weakening; extreme points; destruction start point

2. Кручение стержня из упругопластического материала с разупрочнением

Примем закон связи напряжений и деформаций для материала в следующем виде:

GY , 0 ^ Y ^ Y т , ^T т + G ' ( Y — Y т ) , Y т <  Y ^ Y В , ^т В ^- d g ( Y ^- Y B ) , Y В <  Y ^ Y р , 0, Y р <  Y.

Приведенные соотношения обеспечивают проиллюстрированную на рис. 6 трехзвенную кусочно-линейную аппроксимацию полной диаграммы деформирования: G ' – коэффициент упрочнения материала при сдвиге; τ _В , γ _В – предел прочности при мягком нагружении при чистом сдвиге и соответствующий угол сдвига.

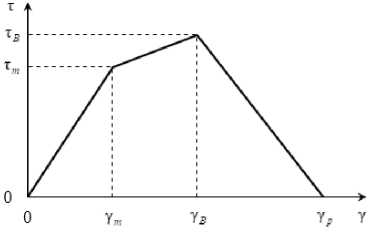
Рис. 6. Диаграмма деформирования материала с участками упрочнения ( y _т <  Y ^ Y В ) и разупрочнения ( y _в <  Y ^ Y _р )

Fig. 6. The deformation diagram for a material with a hardening stage ( y _т <  Y ^ Y В ) and weakening stage ( y _в <  Y ^ Y _р )

γ _В θ

R ,

γ _В θ

ρ р

γ _р θ

R ,

γ р θ

2 р >  R , θ^,

где ρ _т , ρ _В , ρ _р – расстояния от центра сечения до границ упругой зоны, зон пластического упрочнения и за-критической деформации соответственно. В области p _р <  p <  R в случае устойчивого деформирования имеет место полностью разрушенный материал с нулевым сопротивлением внешним нагрузкам.

На стадиях упругого (p _т = p _В = p _р = R ) и упруго-

γ пластического деформирования (p т = —, pВ = p р = R )

уравнение (16) после преобразований совпадает с известными решениями. Получим соотношения, позволяющие определять распределение напряжений в сечении стержня, на стадии закритической деформации.

1. Стадия начальной закритической деформации. Пусть указанная стадия характеризуется тем, что

Y В <  9 R <  y _р , следовательно, p _т

^γ т        ^γ В

—, p = —, p„ = R θ ^В θ ^р

. После преобразования из уравнения (16) следует

M = - A 4 + B - C 9, A = M ^ 9³

θ 3                   3 т

G - G ' G ' + D,.

-----+----G

GG

α4

⁴ M _m G - G' ^G + D G   _Гт ^^

i                a ,                       , a .

3 G G          9 G Y тγт

Экстремальное значение относительного угла поворота сечения найдем из условия равенства нулю производной dM / d θ :

9 * = e.- G - G- + G + D G- a ' , т DD

GG

отметим, что 9 * <  y _р / R , максимум достигается до начала разрушения материала.

в

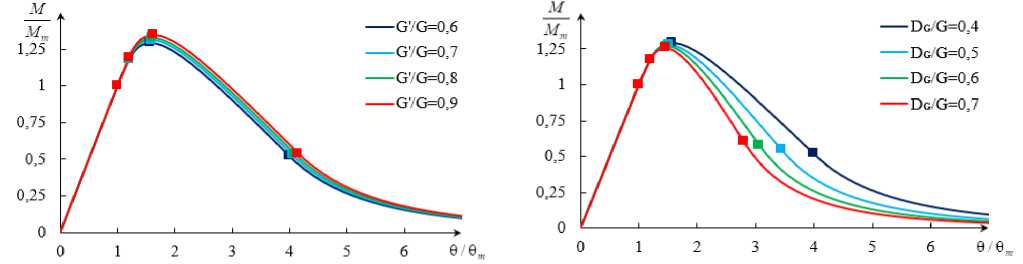
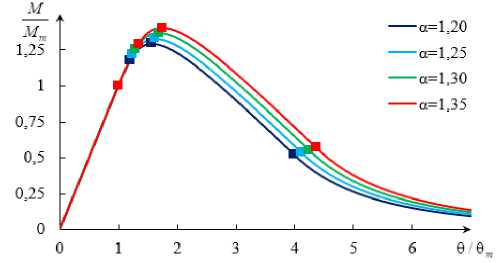
Рис. 7. Графики зависимости крутящего момента от относительного угла поворота сечения для материала с участком упрочнения при разных параметрах: a – G '/ G ; б – D_G / G ; в – α . Маркеры означают (слева направо): момент начала упрочнения; момент начала разупрочнения; момент наибольшего значения крутящего момента; момент начала разрушения

Fig. 7. The dependence of torque on the relative angle of rotation of the cross section for the material with hardening stage with different parameters: а – G '/ G ; b – D_G / G ; c – α . Markers mean (from left to right): the moment the hardening begins; the beginning of weakening; the moment of the greatest value of torque; destruction start point

Данная стадия кончится, когда деформации вблизи поверхности достигнут значения γ _р ; напряжения будут равны нулю. Выразим γ _р через γ _т из уравнения (15):

γ р

Г G - G' G'+ D

—— + _

DD GG a I Y т = eY т

где β – безразмерный коэффициент.

Отметим, что резерв несущей способности конструкции превышает значения, полученные для материала с двухзвенной диаграммой деформирования, в силу наличия зоны упрочнения; значение резерва определяется параметрами диаграммы деформирования материала.

• 2.    Стадия закритической деформации и разрушения. Указанная стадия характеризуется тем, что у р <  9 R ;

γ         γ         γ р

Рт = "т , РВ = "В , Рр =   . ТогДа Уравнение зависи- мости крутящего момента от относительного угла поворота сечения выглядит следующим образом:

М = М 4 [ 1 + 4      (a³ - 1) + G (a 4 - 1) +

т 93 L 3 G (      ) G(      )

+ 3 DG G в ( в³ - a³ ) + G ( a⁴ - e⁴ ) .

Функция монотонно убывает и ограничена снизу нулем.

Графики зависимостей крутящего момента от относительного угла поворота сечения для разных значений коэффициентов G '/ G , D_G / G , α показаны на рис. 7. Из графиков видно, что критическое значение момента и критическое значение относительного угла поворота прямо пропорциональны коэффициентам G '/ G и a = Y в / у т ; обратно пропорциональны коэффициенту D_G / G . При этом наибольшее влияние оказывает α ; коэффициент G '/ G на изменение вида графика влияет слабо. В предельном случае, при a = 1, из данного решения получим решение для упругого материала с разупрочнением.

Заключение

Таким образом, в работе получено новое аналитическое решение задачи о кручении цилиндрического тела круглого поперечного сечения из упругопластического материала с разупрочнением. Были рассмотрены двухзвенная и трехзвенная аппроксимации диаграммы деформирования. Получены соотношения, описывающие распределения деформаций и напряжений на разных стадиях нагружения; приведены эпюры распределения напряжений по сечению. Для двухзвенной диаграммы деформирования получены графики зависимости максимального значения крутящего момента и экстремального значения относительного угла поворота сечения от параметров диаграммы деформирования. Показано, что с уменьшением модуля спада при разупрочнении растет максимальный крутящий момент. Приведены оценки прочностных резервов, связанных с реализацией закри-тической стадии деформирования; показана зависимость резервов от параметров диаграммы деформирования. Построены графики зависимости крутящего момента от относительного угла поворота сечения. Из