Задача о максимальном K-подграфе

Ряд задач дискретной оптимизации эффективно решается для графов, которые состоят из компонент, каждая из которых содержит не более K вершин. Чтобы применить соответствующие алгоритмы для общего случая графов, удалим из графа ряд вершин так, чтобы получившийся подграф состоял из компонент, каждая из которых содержит не более K вершин. Если число удаленных вершин невелико, то рассматриваем все варианты вхождения в решение исходной задачи удаленных вершин (таких вариантов 2 ^q , где q – число удаленных вершин). Сравнивая все варианты, выбираем лучший. Таким образом, задача сводится к определению подграфа, каждая компонента которого содержит не более K вершин (такой подграф назван K-подграфом ). В статье рассматриваются алгоритмы решения задачи определения K- подграфа с максимальным числом вершин (точный алгоритм для дерева и эвристические алгоритмы для случая 2-подграфа ). Приводится пример прикладной задачи формирования портфеля проектов с учетом их взаимозависимости, алгоритм решения которой включает задачу определения максимального K- подграфа.

1.    Постановка задачи

Задан неориентированный граф G с вершинами.

Определение 1. K- подграфом графа G называется подграф, каждая компонента которого содержит не более K вершин.

Определение 2. K- подграф с максимальным числом вершин называется максимальным.

Заметим, что следует отличать 2-подграф как подграф, который является паросочетанием или паросочетание графа, как подмножество ребер, никакие два из которых не имеют общих вершин. На рис. 1 приведены примеры паросочетания (рис. 1а) и 2-подграфа (рис. 1б). Любой 2-подграф является паросочетанием, но не любое паросочетание является 2-подграфом (ребра паросочетания и ребра 2-подграфа выделены толстыми линиями) .

Задача . Определить максимальный K -подграф.

Дадим формальную постановку задачи для 2 - подграфа. Обозначим x i = 1, если вершина i принадлежит 2-подграфу, x i = 0 в противном случае. Задача заключается в максимизации

Ф ( X ) = Z X i                                                                          (1)

i при ограничениях

X i Z X j - 1, i = 1, n ,                                                                                   (2)

jeQi, где Qi – множество вершин, смежных с вершиной i. Задача является задачей квадратичного программирования, для которой не существует эффективных точных методов решения в общем случае.

Информатика и вычислительная техника

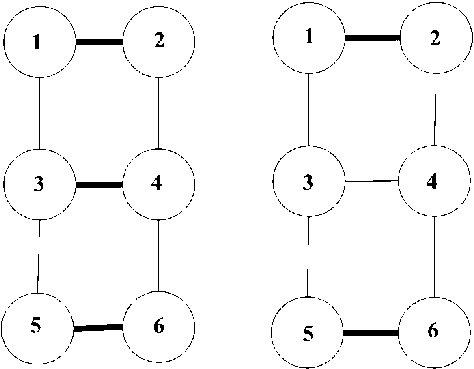
а)                                   б)

Рис. 1. Примеры паросочетания

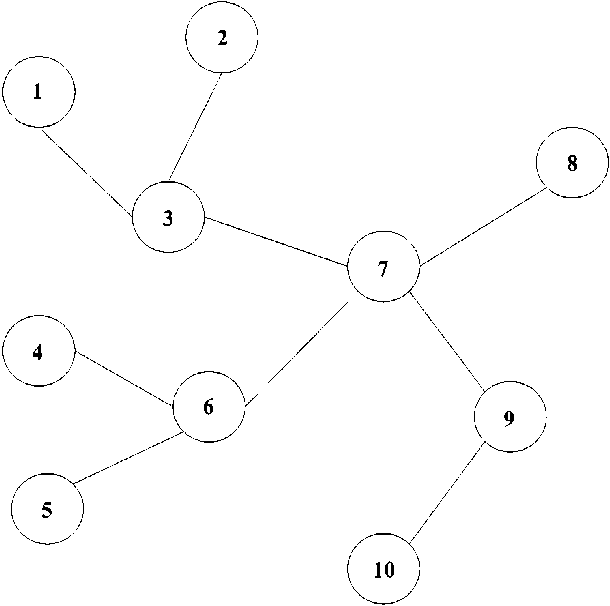
Рис. 2. Пример 1

Определение 3. Степенью куста d называется число его висячих вершин.

Теорема 1 . Если степень куста d = k , то существует оптимальное решение задачи такое, что корневая вершина не входит в K -подграф.

Доказательство. Предположим противное, то есть корневая вершина принадлежит K- подграфу. Если удалить эту вершину, то можно добавить не менее одной висячей вершины, что не меняет общего числа вершин K -подграфа. Это доказывает теорему.

Теорема 2 . Если степень куста d > k , то корневая вершина в оптимальном решении не входит в подграф.

Доказательство. Пусть корневая вершина входит в K -подграф. Удалим эту вершину. В этом случае можно добавить в K -подграф не менее двух вершин. Это доказывает теорему.

Частный случай. Пусть граф G является деревом. В этом случае имеет место Теорема 3.

Теорема 3. Если степень куста d ≤ k – 1, то существует оптимальное решение такое, что корневая вершина принадлежит K -подграфу.

Доказательство. Пусть корневая вершина не принадлежит K -подграфу. В этом случае вершина i , смежная с корневой и не принадлежащая кусту, принадлежит K -подграфу (в противном случае корневая вершина была бы включена в K -подграф). Удаляем вершину i и включаем в K -подграф корневую вершину. Число вершин K -подграфа не изменилось.

Пример 1. Рассмотрим дерево (рис. 2).

Решаем задачу для K = 2. Согласно теореме 1 существует оптимальное решение, в котором вершины 6 и 3 не входят в 2-подграф. После их удаления остаются изолированные вершины 1, 2, 4, 5 и цепь 8, 7, 9, 10. Удалив, например, вершину 9, получаем 2-подграф с семью вершинами. Пусть K = 3. В этом случае, согласно теореме 3, существует оптимальное решение такое, что вершина 7 не принадлежит 3-подграфу. После ее удаления получаем K -подграф с девятью вершинами. Такое решение является оптимальным для любого 3 <  K < 10.

2.    Общий случай

В случае произвольного графа G рассмотрим два эвристических алгоритма решения задачи. Для случая K = 2. Предварительно определим для каждого ребра ( i , j ) ∈ G число вершин m _ij графа G , смежных с этим ребром.

Алгоритм 1 . Определяется ребро ( i , j ) с минимальным m _ij . Это ребро включается в 2-подграф. Удаляются все смежные вершины. Далее процедура повторяется для оставшегося графа до получения 2-подграфа.

Алгоритм 2 . Определяется вершина i с максимальной степенью. Эта вершина исключается из 2-подграфа. Процедура повторяется до получения 2-подграфа.

Замечание . Если по ходу алгоритма встречаются ситуации теорем 1, 2, 3, то применяем соответствующие операции.

Пример 2. Рассмотрим дерево (рис. 3).

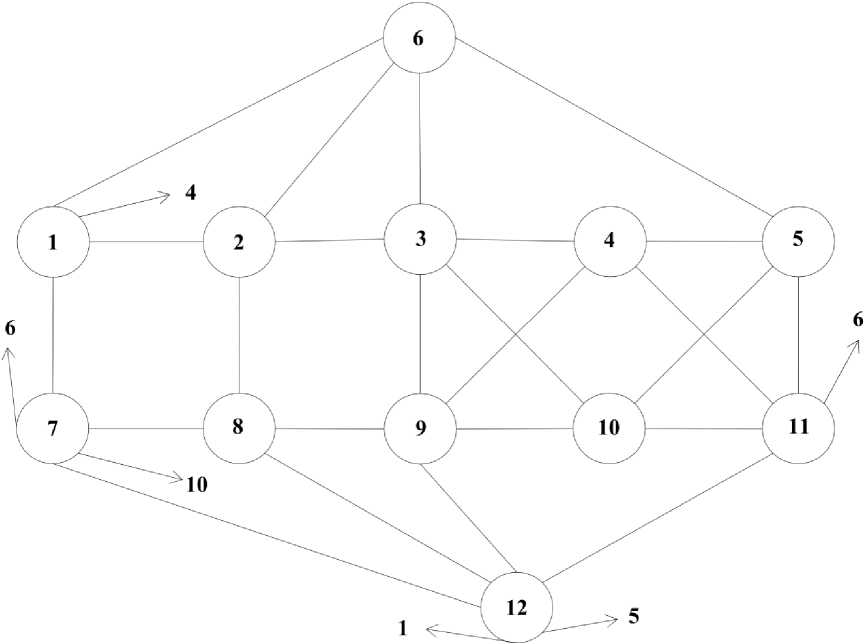
Рис. 3. Пример 2

Информатика и вычислительная техника

Применим алгоритм 1. Ребро (2, 8) имеет минимальную m ₂₈ = 4. Включаем это ребро в 2-подграф. Исключаем ребра (1, 7), (3, 9) и вершины 6 и 12. Остался подграф из четырех вершин 4, 5, 10, 11. Можно включить только одно ребро (например, (4, 10)). Получили 2-подграф с 4 вершинами.

Применим алгоритм 2. Вершины 6 и 12 имеют максимальные степени d В = d 12 = 6. Удаляем вершину 6 и затем 12. Теперь максимальную степень имеют вершины 4 и 10, d 4 = d 10 = 5. Удаляем вершину 4 и затем 10. Ребро (5, 11) включаем в 2-подграф. Из оставшихся вершин максимальные степени имеют вершины 2 и 8. Удаляем вершину 2 и затем 8. Получили 2-подграф с шестью вершинами. Алгоритм 2 позволил получить оптимальное решение.

Пример 3 . Рассмотрим граф (рис. 4).

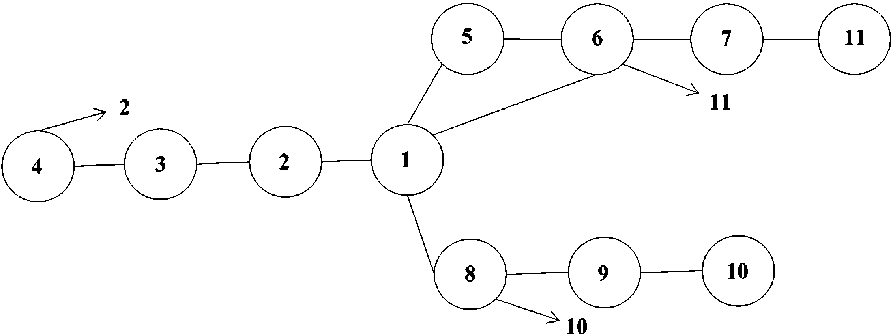
Рис. 4. Пример 3

Применим алгоритм 1. Минимальное m _ij = 2 имеют ребра (4, 3), (7, 11) и (9, 10). Включаем их в 2-подграф. Удаляем вершины 2, 6 и 8. Осталось ребро (1, 5), которое включаем в 2-подграф. Получили 2-подграф с 8 вершинами. Алгоритм 1 дает возможность получить оптимальное решение.

Применим алгоритм 2. Максимальную степень имеют вершины 1 и 6. Удаляем вершину 1 и затем 6. Вершины 5, 7 и 11 включаем в 2-подграф. Далее можно удалить вершины 2 и 10. Получили 2-подграф с 7 вершинами. Полученное решение является оптимальным.

Приведенные примеры позволяют сделать вывод о целесообразности применять оба алгоритма и из полученных решений выбрать лучшее.

3.    Пример прикладной задачи

Рассмотрим пример задачи, в решении которой применяется алгоритм определения максимального K -графа. Речь идет о формировании портфеля проектов. Каждый проект описывается эффектом a_i и затратами с_i . При этом некоторые проекты взаимозависимы в том смысле, что если два проекта i , j включены в портфель, то возникает дополнительный (синергетический) эффект a _ij . Определим граф G взаимозависимостей. Вершины графа соответствуют проектам. Две вершины i , j соединены ребром длины a _ij , если соответствующие проекты взаимозависимы.

Обозначим x i = 1, i = 1, n , максимизирующие

Tax+Zaijxixj(3)

ii при ограничении

Zc-x ^ R,(4)

i где R – величина инвестиционного фонда. Ниже будет показано, что если граф G является паро-сочетанием, то задача эффективно решается при целочисленных значениях параметров методом дихотомического программирования [1, 2]. Возникает идея исключить из графа ряд вершин так, чтобы получить паросочетание, то есть 2-подграф. Далее рассматриваем все варианты включения в портфель исключенных проектов (таких вариантов 2q , где q – число удаленных вершин, и затем выбрать лучшее решение). При небольших q метод достаточно эффективен. Таким образом, задача свелась к определению максимального 2-подграфа.

Пример 4 . Имеются 7 проектов – претендентов на включение в портфель. Данные об эффектах и затратах приведены в табл. 1.

Таблица 1

i	1	2	3	4	5	6	7
a i	12	10	14	9	8	10	6
c i	3	4	7	6	8	12	9

Примем R = 30. Граф взаимозависимостей представлен на рис. 5.

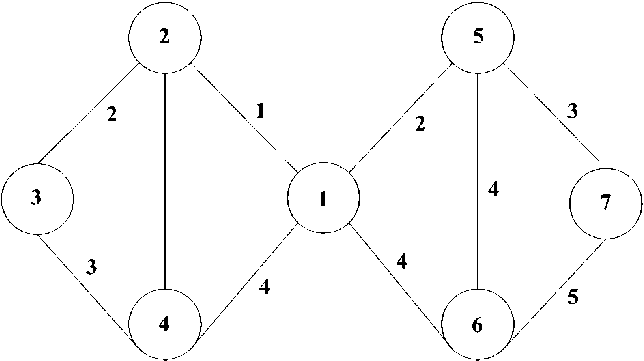
Рис. 5. Граф взаимозависимостей

I этап . Определяем максимальный 2-подграф. Применяем алгоритм 1. Ребра (2, 3), (3, 4), (5, 7) и (6, 7) имеют минимальные m _ij , равные 2. Включаем в 2-подграф. Например, ребра (2, 3) и (5, 7). Удаляем вершины 4, 1 и 6. Получили 2-подграф с четырьмя вершинами. Поскольку число удаленных вершин q = 3, то необходимо рассмотреть 2³ = 8 вариантов.

II этап. Рассматриваем 8 возможных вариантов.

Вариант 1. Ни один из проектов 4, 1 и 6 не включен в портфель. Применяем метод дихотомического программирования [1, 2]. Возьмем структуру дихотомического представления так, чтобы на нижнем уровне рассматривались пары взаимозависимых проектов (рис. 6).

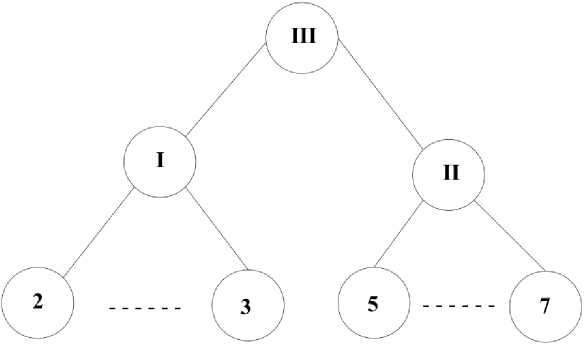
Рис. 6. Дихотомическое представление

Информатика и вычислительная техника

1 шаг. Рассматриваем взаимозависимые проекты 2 и 3. Решение приведено в табл. 2.

Первое число в клетках – это эффект, второе – затраты. В клетке (26; 11) к суммарному эффекту 24 добавлен дополнительный эффект 2. Результаты сведены в табл. 3.

Таблица 2

1	14; 7	26; 11
0	0	10; 4
3 1	0	1

Таблица 3

Объединенный проект I

Вариант	0	1	2	3
Эффект	0	10	14	26
Затраты	6	4	7	11

2 шаг . Рассматриваем проекты 5 и 7. Решение приведено в табл. 4. Результаты сведены в табл. 5. Вариант (6; 9) исключен, поскольку он доминируется вариантом (8;8).

Таблица 4

1	6; 9	17; 17
0	0	8; 8
7 5	0	1

Таблица 5

Объединенный проект II

Вариант	0	1	2
Эффект	0	8	17
Затраты	0	8	17

3 шаг . Рассматриваем объединенные проекты I и II. Решение приведено в табл. 6.

Таблица 6

2	17; 17	27; 21	31; 24	43; 28
1	4; 2	18; 12	22; 15	34; 19
0	0	10; 4	14; 7	26; 11
II I	0	1	2	3

Максимальный эффект 43 достигается при затратах 28.

Вариант 2 . Проект 1 включен в портфель. Решаем задачу аналогично предыдущему варианту, добавив к эффектам проектов 2 и 5 дополнительные эффекты 1 и 2 соответственно. Приведем только результат. Максимальный эффект равен 35 при затратах 22.

Вариант 3 . Проект 4 включен в портфель. Добавляем к эффектам проектов 2 и 3 дополнительные эффекты 2 и 3 соответственно. Приведем результат. Максимальный эффект равен 32 при затратах 26.

Вариант 4 . Проект 6 включен в портфель. Добавляем к эффектам проектов 5 и 7 дополнительные эффекты 4 и 5. Приведем результат. Максимальный эффект равен 26 при затратах 23.

Вариант 5 . Проекты 1 и 4 включены в портфель. Добавляем к проктам 2, 3 и 5 дополнительные эффекты 3, 3 и 2 соответственно. Учитываем также дополнительно эффект 4 взаимозависимых проектов 1 и 4. Приведем результат. Максимальный эффект равен 67 при затратах 28.

Вариант 6 . Проекты 1 и 6 включены в портфель. Добавляем к проектам 2, 5 , 7 дополнительные эффекты 1, 6, 5 соответственно. Приведем результат. Максимальный эффект равен 28 с затратами 30.

Вариант 7 . Проекты 4 и 6 включены в портфель. Добавляем к проектам 2, 3, 5, 7 дополнительные эффекты 2, 3, 4 и 5 соответственно. Учитываем дополнительный эффект 4 взаимозависимых проектов 1 и 6. Приведем результат. Максимальный эффект равен 33 при затратах 29.

Вариант 8. Проекты 1, 4 , 6 включены в портфель. Добавляем к проектам 2, 3, 5, 7 дополнительные эффекты 3, 3, 6 и 5 соответственно. Учитываем также дополнительно эффекты 4 и 4 от взаимозависимых проектов 1, 4 и 1, 6 соответственно. Приведем результат. Максимальный эффект равен 25 при затратах 28.

Сравнивая, получаем, что наилучшим является вариант 5 с эффектом 67, то есть в портфель включены проекты 1, 2, 3, 4, 5.

Рассмотрим теперь возможность решения задачи на основе 3 подграфов. Из рис. 5 видно, что, удалив вершину 1, мы получаем 3-подграф из 6 вершин. В данном случае необходимо рассмотреть два варианта вместо 8 в предыдущем случае. Однако при этом требуется определенная модификация метода дихотомического программирования. Рассмотрим ее на примере более подробно.

Вариант 1 . Проект 1 не включен в портфель.

1 шаг . Рассматриваем компоненту 1 из вершин 2, 3, 4. Возьмем структуру дихотомического представления задачи, представленную на рис. 7.

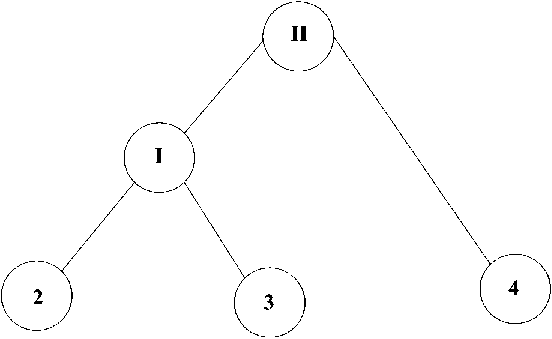
Рис. 7. Структура дихотомического представления

Рассматриваем проекты 2 и 3. Решение приведено в табл. 7. Результаты приведены в табл. 8.

Таблица 7

1	14; 7	26; 11
0	0	10; 4
3 2	0	1

Таблица 8

Объединенный проект I

Вариант	0	1	2	3
Эффект	0	10	14	26
Затраты	6	4	7	11
Эффект от 4	0	2	3	5

Последняя строка показывает эффект от проекта 4, если он будет включен в портфель. В этом суть модификации метода дихотомического программирования. Рассматриваем объединенный проект I и проект 4. Решение приведено в табл. 9. Результаты приведены в табл. 10.

Таблица 9

1	9; 6	21; 10	26; 13	40; 17
0	0	10; 4	14; 7	26; 11
4 I	0	1	2	3

Таблица 10

Компонента 1

Вариант	0	1	2	3	4	5
Эффект	0	10	14	21	26	40
Затраты	0	4	7	10	11	17

2 шаг . Рассматриваем компоненту 2 из вершин 5, 6, 7. Рассматриваем проекты 5 и 6. Решение приведено в табл. 11. Результаты представлены в табл. 12.

Информатика и вычислительная техника

Таблица 11

1	10; 12	22; 20
0	0	8; 8
6 5	0	1

Таблица 12

Объединенный проект I

Вариант	0	1	2	3
Эффект	0	8	10	22
Затраты	0	8	12	20
Эффект от 7	0	2	4	6

Рассматриваем объединенный проект I и проект 7. Решение приведено в табл. 13. Результаты представлены в табл. 14.

Таблица 13

1	6; 9 *	16; 17	20; 21 *	34; 29
0	0	8; 8	10; 12	22; 20
7 I	0	1	2	3

Таблица 14

Компонента 2

Вариант	0	1	2	3	4	5
Эффект	0	8	10	16	22	34
Затраты	0	8	12	17	20	29

3 шаг . Рассматриваем компоненты 1 и 2. Решение приведено в табл. 15.

Таблица 15

5	34; 29	–	–	–	–	–
4	22; 20	32; 24	36; 27	43; 30	–	–
3	16; 17	26; 21	30; 24	37; 27	42; 28	–
2	10; 12	20; 16	24; 19	31; 22	36; 23	50; 29
1	8; 8	18; 12	22; 15	29; 18	34; 19	48; 25
0	0	10; 4	14; 7	21; 10	26; 11	40; 17
2 1	0	1	2	3	4	5

Максимальный эффект равен 50.

Вариант 2. Проект 1 включен в портфель. Рассматриваем компоненту 1. Берем структуру дихотомического представления рис. 7. Рассматриваем проекты 2 и 3, добавляя к проекту 2 дополнительный эффект от проекта 1. Решение приведено в табл. 16. Результаты представлены в табл. 17.

Таблица 16

1	14; 7	27; 11
0	0	11; 4
3 2	0	1

Таблица 17

Объединенный проект I

Вариант	0	1	2	3
Эффект	0	11	14	27
Затраты	0	4	7	11
Эффект от 4	0	2	3	5

Рассматриваем объединенный проект I и проект 4. Решение приведено в табл. 18. Результаты представлены в табл. 19.

Таблица 18

1	13; 6	26; 10	30; 13	45; 17
0	0	11; 4	14; 7	27; 11
4 I	0	1	2	3

Таблица 19

Компонента 1

Вариант	0	1	2	3	4	5	6	7
Эффект	0	11	13	14	26	27	30	45
Затраты	0	4	6	7	10	11	13	17

2 шаг . Рассматриваем компоненту 2 из вершин 5, 6 и 7. Рассматриваем проекты 5 и 6. Решение приведено в табл. 20. Результаты представлены в табл. 21.

Таблица 20

1	14; 12	28; 20
0	0	10; 8
6 5	0	1

Таблица 21

Объединенный проект I

Вариант	0	1	2	3
Эффект	0	10	14	28
Затраты	0	8	12	20
Эффект от 7	0	4 *	5	9

Рассматриваем объединенный проект I и проект 7. Решение приведено в табл. 22. Результаты представлены в табл. 23.

Таблица 22

1	6;9 *	20;17	25;21 *	43;29
0	0	10;8	14;12	28;20
7 I	0	1	2	3

Компонента 2

Таблица 23

Вариант	0	1	2	3	4
Эффект	0	10	14	20	28
Затраты	0	8	12	17	20

3 шаг . Рассматриваем компоненты 1 и 2. Решение приведено в табл. 24.

Таблица 24

4	28; 20	39; 24	41; 26	42; 27	–	–	–	–
3	20; 17	31; 21	33; 23	34; 24	46; 27	47; 28	–	–
2	14; 12	25; 16	27; 18	28; 19	40; 22	41; 23	44; 25	–
1	10; 8	21; 12	23; 14	24; 15	36; 18	37; 19	40; 21	55; 25
0	0	11; 4	13; 6	14; 7	26; 10	27; 11	30; 13	45; 17
2 1	0	1	2	3	4	5	6	7

Максимальный эффект равен 55 + 12 = 67. Выбираем вариант 2. Состав портфеля определяем методом обратного хода. Клетке (55, 25) соответствует вариант 7 компоненты 1 и вариант 1 компоненты 2. Варианту 7 компоненты соответствует включение в портфель проектов 2, 3 и 4. Варианту 1 компоненты 2 соответствует включение в портфель проекта 5. Вместе с проектом 1 получаем, что в портфель включаются проекты 1, 2, 3, 4, 5, что и было получено ранее.

Информатика и вычислительная техника

Заключение

Введенное понятие K -подграфа оказалось полезным, как показывает решение задачи формирования портфеля взаимозависимых проектов, особенно при решении целочисленных задач квадратичного программирования. Требует дальнейших исследований задача определения максимальных K -подграфов, особенно для случаев K > 2. Представляет также интерес поиск прикладных задач, эффективно решаемых, если соответствующий граф является K -графом. Заметим также, что, как показывает пример прикладной задачи, в ряде случаев использование 3-подграфа эффективнее, чем использование 2-подграфа.

Действительно, при использовании 2-подграфа в каждом варианте делаются три элементарных шага. Поскольку вариантов 8, то требуется 24 элементарных шага. При использовании 3-подграфа число вариантов равно 2. Однако для каждого варианта требуются 7 элементарных шагов (по три шага для каждой компоненты и один шаг для обоих компонент). В целом получаем 14 элементарных шагов, что меньше 24.