Задача о предписанной точке минимума

Проблема получения и рационального использования данных наблюдений остается актуальной на протяжении многих десятилетий. По мере развития мощных современных вычислительных и измерительных средств технологии анализа и обработки данных находят всё более широкое применение в различных областях науки и практики. К числу таких методик относится процедура ассимиляции (усвоения) данных наблюдений, представляющая собой обратную задачу или задачу оптимального управления об идентификации распределённых параметров математических моделей. Как известно, сами модели могут лишь приближённо отображать природные процессы, поэтому их необходимо периодически «подправлять» данными наблюдений. С другой стороны, наблюдаемые поля, неизбежно неполные и зашумлённые, нуждаются в исправлении путём их усвоения в подходящей математической модели. Метод ассимиляции данных наблюдений имеет следующую общепринятую вариационную трактовку: определяется функционал стоимости, измеряющий расхождение между наблюдаемыми величинами и результатами моделирования, после чего разыскиваются те неизвестные характеристики модели, для которых функционал стоимости принимает своё наименьшее возможное значение [1 --17]. Задача ассимиляции данных эквивалентна в определенном смысле некорректно поставленным задачам, что обуславливает трудности её решения и одновременно приводит к необходимости привлечения здесь методов регуляризации. Исследования последних лет показывают высокую чувствительность решений к ошибкам в данных измерений [18--20]. В связи с этим большое значение приобретают вопросы разработки новых принципов вариационной ассимиляции данных, в частности представляет интерес исследование следующей «задачи о предписанной точке минимума». Пусть точно известно начальное состояние системы u0 , а распределенное внешнее воздействие f требуется определить с помощью целевого функ- ционала стоимости S (и), где u = u (и0; f) — решение системы. При поиске неизвестной функции f мы будем руководствоваться следующими соображениями:

• 1)    потребуем, чтобы при данном фиксированном f функционал S ( и ) нельзя было уменьшить, выбирая вместо u 0 какое-либо другое начальное состояние. Иначе говоря, u 0 является предписанной заранее точкой минимума, и нам подходят только те функции f , для которых этот минимум имеет место;

• 2)    среди всех f , удовлетворяющих условию 1, мы выберем ту функцию, на которой S ( и ) принимает свое наименьшее возможное значение.

Разумеется, функционал S ( и ) можно было бы уменьшить, если отказаться от требования 1 и провести оптимизацию по всему пространству. Поэтому рассматриваемый здесь алгоритм характеризует ситуацию, в которой информация о начальном состоянии u 0 считается гораздо более достоверной, чем содержащаяся в S ( и ) информация о данных наблюдений. К тому же сам функционал S ( и ) обычно включает в себя регуляризующие добавки, которые никак не связаны с наблюдаемыми полями, но позволяют корректно поставить задачу и эффективно организовать вычисления. В этом случае становится очевидным, что наименьшее значение функционала еще не означает наилучшего согласования с наблюдениями, и кажется вполне разумным требование о существовании предписанной точки минимума.

В настоящей работе исследуются вопросы существования и единственности решения задачи (1) --(2) и вычисляются собственные значения основного оператора задачи, входящего в уравнение для управления. Полученные результаты применяются в разделе IV для построения алгоритма численного решения задачи на примере одномерного уравнения теплопроводности.

II.    Постановка задачи.

Существование и единственность решений

Пусть A — не зависящий от времени линейный замкнутый оператор, действующий в гильбертовом пространстве H с областью определения, плотной в H . Будем предполагать, что A — неограниченный самосопряженный положительно определенный оператор в H , имеющий вполне непрерывный обратный оператор. Обозначим: [ • , • ] — скалярное произведение в H ; X ^а , а Е R — гильбертовы пространства со скалярным произведением [ u,v ] _а = [ A ^a u,A ^a v ]; Y ^а = L 2 (0 ,T ; X ^а ), где T <  + те , Y = Y ⁰ = L 2 (0 ,T ; H ); ( • , • ) а , || • || _а — скалярное произведение и норма в Y ^а ; W = { u Е Y ^а+1 / ² , du Е Y ^а- ¹ / ² } ; W * — сопряженное с W пространство при отождествлении Y со своим сопряженным пространством.

Пусть { w _n } — полная ортонормированная система в H , составленная из собственных функций A : Aw n = A n W n , A n >  0, A n ^ + те при n ^ те .

Рассмотрим эволюционную задачу d^ + Au = J, t Е (0,T);

u(0) = u0, ее разрешающий оператор G : Xа x Yа-1 /2 ^ W определим равенством u =    G (u0; f)

• V u 0 Е X ^a V f Е Y ^a- ¹ / ² . Пусть Q 0 : X ^а ^ W и Q : Y ^a- ¹ / ² ^ W есть сужения G на множества X ^а x { 0 } и { 0 } x Y ^{а 1} / ² соответственно. Сопряженные операторы Q 0 : W * ^ X ^а и

• Q* : W* ^ Y1 /2-а определим соотношениями

( Q о y,g ) = [ y,Q * g ] а V y е x ^а V g е w * ,

( Qf,g ) = ( f,Q * g ) V f е y ^{a - 1} / ² V g е w * .

Заметим, что для g Е Y ^{а - 1} / ² значения Q * g и Q * g задаются равенствами

Q0 g = A-2 а q (0), Q* g = q, где q есть решение задачи — dq + Aq = g, q(T) = 0.

Пусть на W задан функционал

S ⁽ u ) = y n u t ⁺ Au ^— f “ ^ a- 1 / 2 ⁺

• ⁺2 n u n a +1 / 2 ⁺^ i i u ^— u i i i , где y >  0, о ^ 0, в d а + 1 / 2, f “ — некоторое априорно известное приближенное значение f .

При заданных u 0 Е X ^a u Е Y ¹ , f “ Е Y ^{a - 1} / ² введем множество F всех функций f Е Y ^{a - 1} / ² , для которых S ( G ( u 0 ; f )) d S ( G ( v 0 ; f )) V v 0 Е X ^a .

Лемма 1. Множество F слабо замкнуто в Y α- 1 / 2 .

Доказательство. Функция f Е y ^{a - 1} / ² принадлежит F , если первая вариация S ( u ) равна нулю на u = G ( u о ; f ) для всех v Е Q о X ^a :

dS ( u + 9Q о w о ) dθ

= о ( A ^{a +1} / ² u,A ^{a +1} / ² Q о w о )+

θ =0

+ (A1 (u — u),AiQоwо) = 0 Vwо Е Xa. (1) Пусть fn Е F и fn ^ f слабо в Ya-1 /2. Из ограниченности операторов Q и Q0 вытекает, что un = G(uо; fn) ^ u слабо в Ya+1 /2. Поэтому для u остается справедливым равенство (1).

Задача о предписанной точке минимума дится к отысканию функции f такой, что f Е F;

S ( G ( u о ; f )) <  S ( G ( u о ; g )) V g Е F.

сво-

Имеет место следующая теорема существования и единственности.

Теорема 1. Если y >  0, о >  0, в d а +1 / 2 или Y >  0, о ^ 0, в = а +1 / 2, то задача (2) — (3) имеет единственное решение при всех u о Е X ^а , u Е Y ¹ , f “ Е Y а- 1 / 2

Доказательство. Покажем, что множество F не пусто. Возьмем v _n = Q _о w _n = exp( — A _n t ) w _n , тогда (1) принимает вид

5S ( u ) v _n = о ( u,A na ⁺¹ v n )+( u — u,A n¹ v _n ) = 0 V n Е N .

Обозначим через dn (t) = exp(—Ant) — exp( An (t — 2 T)),

T cn = |dn (t) dt =

= -^(1 — exp(—4 AnT)) — 2 T exp(—2 AnT), 2An mn = 2( oA na + A 2n 1).

Из уравнения — q t + Aq = v _n , q ( T ) = 0, находим q = q n = 21 П d n ( t ) W n .

Используя равенство

(u,vn ) = (f,qn ) + 2A(_(1 — eXP( — 2 AnT))[u о ,wn], имеем

+ m n (1

то есть

T

5S ( u ) v n = m n | d n ( t )[ f,W n ] dt +

— exp( — 2 A n T ))[ u о ,W n ] — A n¹ ( u ,v n ) = 0 ,

T

I d n ( t )[ f,W n ] dt =

λ ^{2 β}

= -n - ( u ,V n ) — (1 — exp( — 2 A n T ))[ u о ,W n ] .

m n

Следовательно, минимальное по норме L ₂ (0 ,T ) значение [ f,w _n ] равно

T

• ; _    1 / A 2 ¹

f n ( t ) = — — exp( — A n t )[ u ,W n ] dt — c n m n

• — (1 — exp( — 2 A n T ))[ u о ,W n ]^ d n ( t ) .

Нетрудно проверить, что функция

∞ f = Е fn (t) Wn n=1

принадлежит Y ^{a 1} / 2 . Действительно, c n > 1 / (4 A n ) при достаточно больших n , тогда

2 ^∞

1f 1 a- 1 / 2 = E A"- 1 f') dt < n=1

c _n

∞

< E a na- ¹

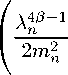
T

| [ u,W n ] ² dt + [ u 0 w ] ²

<

T

∞  2α+2β-1

< E          A ne [ u,Wn]2 dt+SE A na [ u о wn]2 < n=1   mn   0

< c luнe+8[ u o]a, где c = 4/a2 при в < a — 1 /2 и c = 4/(a + 1)2 при в = a — 1 / 2.

По построению f e F. Теперь осталось заметить, что множество F слабо замкнуто в Y α-1/2, функционал J(f) = S(G(u0; f)), f e F, является строго выпуклым и слабо полунепрерывным снизу в Y α-1/2 , а любая его минимизирующая по- следовательность ограничена, из чего следует, что

J(f) имеет на F точку минимума и эта точка ми- нимума единственна.

= y ( A ^a- ¹ / ² ( f — f a ) ,A ^{a - 1} / ² g )+

+ a ( A ^{a +1} / ² u,A ^{a +1} / ² Qg ) + ( A ^e ( u — u) ,A ^e Qg ) =

= y ( A ^{2 a}- ¹ ( f — f a ) ,g ) + ( Q * ( Bu — A ^{2 e} u ) ,g ) = 0

V g e F 0 .

Заметив, что ( Q * BQ 0 u 0 ,g ) = ( u 0 ,Q * BQg ) = 0, преобразуем последнее равенство к виду

Y ( A ^{2 a}- ¹ ( f — f a ) ,g ) + ( Q * ( BQf — A ^{2 e} u ) ,g ) =

= ( Df — yA ^{2 a}- ¹ f a — Q * A ^{2 e} u,g ) = 0 V g e F 0 .

Таким образом, (5) равносильно тому, что функция Df — yA ^{2 a}- ¹ f a — Q * A ^{2 e} u ортогональна ядру оператора Q ^∗ ₀ BQ . Тогда эта функция принадлежит области значений сопряженного оператора Q * BQ 0 , то есть существует r 0 e X ^a , для которого

Df — yA ^{2 a}- ¹ f a — Q * A ^{2 e} u = Q * BQ 0 r 0 .   (6)

Исключая f из системы (4), (6), получаем для управления r 0 уравнение

Mr 0 = П,

где

M = Q 0 BQD - ¹ Q * BQ 0 ,

П = Q * ( A ^{2 e} u — BQ 0 u 0 — BQD - ¹ ( yA ^{2 a}- ¹ f a + Q * A ^{2 e} u )) .

Теорема 2. Если выполнены условия теоремы 1, то

1) оператор M имеет собственные функции w _n , отвечающие собственным значениям

III. Собственные функции и собственные значения основного оператора задачи

M n =

( a + A n^{e - 2 a}- ¹ )

1 — exp( — 2 A n T )

A n (1 — exp( — 2 a n T ))

Обозначим через B = aA ^{2 a +1} + A ^{2 в} . D = ya ^{2 a}- ¹ + Q * BQ . Условие (1) можно записать в виде

a n + A n + ( a n — A n ) exp( — 2 a n

. t )] ,

( Bu — A ^{2 e} u ,Q 0 w 0 ) = [ Q 0 ( Bu — A ^{2 e} u ) ,w 0 ] = 0

где a n = A n ^ 1 + ( a + A n^{e 2 a 1} ) /y ;

2) решением задачи (2) — (3) является функция

Vw о e Xa, что равносильно уравнению Q0(Bu — A2eu) = 0, то есть

Q 0 BQf = Q 0 ( A ^{2 e} u — BQ о u 0 ) , (4)

Обозначим через F 0 множество всех допустимых приращений g = f — f , где f, f e F . Из (4) вытекает, что приращения удовлетворяют уравнению Q 0 BQg = 0, то есть F 0 совпадает с ядром оператора Q ^∗ ₀ BQ . Условие (3) можно записать как

f = D-1 Q*A2eu + E ППyn(t)wn, n=1 μn f = D-1 Q*A2 e u+

1 ^ f n

+— E —(exp( — a n t ) — exp( a n ( t — 2 T ))) w n , γ ₌₁ μ n

в которой

T

A 2 в- 2 a                    1

nn = -n      hn(t)u ndt — ^(a + A ne-2 a-1) X hn(0)                 2

S ( u ) <  S ( u + Qg ) V g e F 0 .        (5)

X ^{(1 — ex}p^{( — 2 A} n ^T )) u 0 ,n ^—

Рассмотрим первую вариацию S ( u ) относительно переменной f :

T

A^ |y n ⁽ t ) f n dt,

6S ^{( u} ) g =

dS ( u + 6Qg ) dθ

θ =0

hn(t) = (an+An)exp(—ant)+(an—An) exp(an (t—2T)), un = [ u ,wn ], u 0 ,n = [ u 0 ,wn ], fn = [ f awn ],

У п ( t ) =

А П ( а + А Т ^{2 а -} 1 ) _х

Yh n (0)

где h(t) = (A + a) exp(—at) + (a — A) exp(a(t — 2T)). Далее воспользуемся равенствами х [exp(-ant) — exp(an(t — 2T))].

Доказательство. Пусть w — собственная функция A , Aw = Aw , вычислим для неё значение Mw . Повторяя рассуждения теоремы 1, находим Q * BQ 0 w = 2 у У ( t ) w , где b = аА ^{2 а} +1 + A ^{2 в} , У ( t ) = exp( — At ) — exp( A ( t — 2 T )).

Для ^ = D-1Q* BQ о w имеем уравнение yA 2 a-1 e + bQ*Q^ =     (t) w.        (8)

Будем искать его решение в виде £ = У (t) w■ Поскольку Q*Qe = 0 при t = T, то из (8) находим у(T) = 0. Подействовав на обе части (8) оператором — d + A, получаем уравнение yA 2 а 1( —у' + Ay) w + bQ^ = b exp(—At) w.   (9)

Следовательно, — у' (0) + Ay (0) = bA ¹ - ^{2 a} /y ■ Подействовав теперь на (8) оператором d + A , приходим к уравнению yA ^{2 a - 1} ( — у " + A ² у ) + by = 0, то есть у '' = a ² у , где a = У А ² + bA ¹ - ^{2 а} /y ■ С учетом начальных условий находим его решение:

_       b (exp( — at ) — exp( a ( t — 2 T )))

^{у (} t ) = yA ² a ^- 1 ( A + a + ( a — A ) exp( — 2 aT )) ^.

Далее рассмотрим уравнение — qt+Aq = bQy (t) w, q(T) = 0. Его решением будет q = z(t)w, где —z'' + A2z = Ьу(t), z(T) = 0, —z'(0) + Az(0) = 0, то есть       z (t ) = A 2 a+1( а + A 2 e-2 a-1) х exp(—At) — exp( A (t — 2 T))

х.              2a exp(—at) — exp( a (t — 2 T)) 1

A + a + ( a — A ) exp(—2 aT )

Заметив, что Mw = A ^{- 2 a} z (0) w , получаем собственные значения M .

Для того чтобы построить разложение П = 52 ^ =1 n n w n для функции в правой части (7), вычислим

[ n,w ] = [ П,А ^{- 2 a} w ] a =

= ( A ^{2 в} u — BQ о u о — BQD ^- 1 ( yA ^{2 a - 1} f a +

+ Q * A ^{2 e} u ) ,Q о A ^{- 2 a} w ) =

= a ^{2 e - 2 a} ( u ,q о w ) — bA ^{- 2 a} ( Q о u о ,Q о w ) —

— ( yA ^{2 a - 1} f a + Q * A ^{2 e} u ,D ^{- 1} Q * BQ о A ^{- 2 a} w ) =

= a ^{2 e - 2 a} ( u ,q о w — Qy ( t ) w ) — bA ^{- 2 a} ( Q о u о ,Q о w ) —

^— y^{a - 1 (} f ^{а ,}у ⁽ t ) ^w ) =

T

A 2 в- 2 a                    1

——— h ⁽ t ^{)[ u,w ] dt —} -^{( а + A 2 в - 2 a -} 1 ) ^х h (0)                    2

oo rо = 52 nnwn/^n n=1

и D ^{- 1} Q * BQ о w = у ( t ) w для вычисления f = D ^- 1 ( Q * A ^{2 в} й + Q * BQ о r _о ), что завершает доказательство теоремы.

Ниже мы подробно рассмотрим алгоритм численного решения задачи (2) — (3) на примере одномерного уравнения теплопроводности для частного случая а = 1 / 2, в = 0.

Алгоритм численного решения задачи.

В ограниченной области П = (0,L) х (0,T), T < + го, рассмотрим одномерное уравнение теплопроводности f ut — uxx = f (x,t), x E (0,L), t E (0,T),

[ u (0 ,t ) = u ( L,t ) = 0 , u ( x, 0) = u о ( x ) .

Будем обозначать через H действительное пространство L 2 (0 ,L ) со скалярным произведением L

[ u.v ] = J u ( x ) v ( x ) dx и нормой [ u ] = У [ u,u ] и через 0

Y действительное пространство L ₂ (П) со скалярным произведением ( u.v ) = J J u ( x,t ) v ( x,t ) dxdt

Ω и нормой || u || = У(u,u). Введем пространство X = {u(x) : u E H,du/dx E H,u(0) = u(L) = 0}.

Обозначим через A сужение оператора ( — d ² /dx ² ) на класс функций, равных нулю на концах отрезка [0 ,L ], и через w n = w n ( x ) = sin( nnx/l ), A n = ( nnx/l ) ² , где l = L/ 2, собственные функции и собственные значения A . Оператор A ² введем следующим образом: если u = ^2 0 =1 u n w n ( x ), то A ² u = ^ 0 =1 A 0 u n w n ( x ).

Как и ранее, будем предполагать, что имеются данные наблюдений u ( x,t ) за поведением решения (10), которые используются для отыскания неизвестной правой части f ( x,t ) при заданном начальном состоянии u о ( x ). Определим функционал стоимости:

S(u) = 2 lut + Au — fa|2 + а |Au|2 + 2 |u — u|2 , где γ , σ — неотрицательные параметры регуляризации, fa E L2(П) — некоторое априорно известное приближенное значение f.

Для всех f E Y , v о E X обозначим через z = Qf и v = Q о v о решения задач

Г z t ⁺ Az = ^f, x ^{E (0} ,L ) , t ^{e (0 ,T} ) , [ z (0 ,t ) = z ( L,t ) = 0 , z ( x, 0) = 0 ,

T

х (1 — exp( — 2 AT ))[ u о ,w ] — A |у ( t )[ f a ,w ] dt,

( v t + Av = 0 , x E (0 ,L ) ,t E (0 ,T ) , [ v (0 ,t ) = v ( L,t ) = 0 , v ( x, 0) = v _о .

В этих обозначениях решение задачи (10) записывается как u = Qf + Q о и о . Сопряженные линейные операторы Q ^∗ и Q ^∗ ₀ определим соотношениями Q * g = q , Q o g = q ( x, 0), где функция q = q ( x,t ) есть решение задачи

( ^{- q} t ⁺ Aq = g, ^{x E (0 ,L} ) , t E ^{(0 ,T} ) ,

I q (0 ,t ) = q ( L,t ) = 0 , q ( x,T ) = 0 .          ⁽ )

Интегрируя по частям, нетрудно проверить, что выполняются равенства

( Qf,g ) = ( f,Q * g ) , ( Q о v о ,g ) = [ v о ,Q 0 g ] .

Для целей дальнейшего исследования введем также операторы B = E + oA 2 , где E — тождественный оператор, D = yE + Q * BQ , M = Q 0 BQD - ¹ Q * BQ о .

Сформулированное во введении условие 1 можно записать в виде

S ( и ) <  S ( и + Q о v о )     V v о E X. (12)

Рассмотрим первую вариацию S ( и ) относительно переменной u 0 :

dS ( и + 6Q о v о ) dθ

= o ( Au,AQ о v о )+( и - U ,Q о v о ) = θ =0

= ( Ви - U,Q о v о ) = [ Q 0 ( Ви - и ) ,v о ] = 0

V v о E X.

Таким образом, (12) равносильно уравнению

Q 0 ( Ви - и ) = 0, то есть

Q 0 BQf = Q * и - Q ^ BQ о и о .      (13)

В теореме 1 показано, что множество F функций, удовлетворяющих (13), не является пустым при любых и о E X , и E Y . Обозначим через F о множество всех допустимых приращений g = f - f , где f,f E F . Из (13) вытекает, что приращения удовлетворяют уравнению Q 0 BQg = 0, то есть F о совпадает с ядром оператора Q ^∗ ₀ BQ .

Сформулированное во введении условие 2 можно записать в виде

S ( и ) <  S ( и + Qg ) V g E F о .       (14)

Рассмотрим первую вариацию S ( и ) относительно переменной f :

6S ^{( и} ) g =

dS ( и + 6Qg ) dθ

θ =0

= Y ( f - f a ,g ) + o ( Au,AQg ) + ( и - и,Qg ) =

= Y ( f - f a ,g ) + ( Bu - и,Qg ) =

= Y ( f - f a ,g ) + ( Q * ( Bu - U),g ) = 0 V g E F о . (15)

Заметим, что ( Q * BQ _о и _о ,g ) = ( и _о ,Q * BQg ) = 0, поэтому (15) преобразуется к виду

= ( Df - Yf a - Q * U,g ) = 0 V g E F о .

Таким образом, (14) равносильно тому, что функция Df - Yf a - Q*U ортогональна ядру оператора Q0BQ. Тогда Df - Yfa - Q*U принадлежит области значений сопряженного оператора Q∗BQ0, то есть существует функция rо(x), для которой Df - Yf a - Q*U = Q* BQ о r о. Выражая из последнего соотношения f = D- 1(Q*U + Yf a) + D-1 Q*BQ о r о    (16)

и подставляя результат в (13), получаем уравнение для определения r о ( x ):

Mr о = П,               (17)

где

П = Q 0 ( U - BQD ^- 1 ( Yf a + Q * U ) - BQ о и о ) . (18)

Из доказательства теоремы 2 вытекает, что оператор M имеет собственные функции w n ( x ), отвечающие собственным значениям

^ n ^ n ^{( o +} ^ _n ) ^

^ [ 1 - exp( - 2 X n T )

X n ^{(1 -} exp^{( - 2} a n T ))       1

a n + X n + ( a n - X n ) exp( - 2 a n T )

где a n = X n 1 + ( o + X n ² ) /y .

Таким образом, вычислив функцию П ( x ) = 52 ^ =1 n n w _n ( x ), мы можем найти решение уравнения (17) по формуле

∞ rо(x ) = ^ nn Wn (x), μn n=1

а затем найти f ( x,t ) в соответствии с (16).

При реализации алгоритма необходимо обращать оператор D = YE + Q ^* BQ , который является самосопряженным и положительно определенным. Действительно, обозначив через z = Qf , z 1 = Qf 1 , имеем

( Df,f 1 ) = Y ( f,f 1 ) + ( z,z 1 ) + o ( Az,Az i ) = ( f,Df i ) ,

( Df,f )= Y \\ f II 2 + ll z ll 2 + o \\ Az || ² >Y ll f || 2 .

Для оценки сверху спектра оператора D воспользуемся равенствами

^{( f,z} ) = ⁽ z t ⁺ A^z,z ) > ⁽ A^z,z ) ,

(f,Az) = (Zt + Az,Az) > llAzll2 Vz E QY, из которых следует, что llzll2 < (Az,z)/X1 < (f,z)/X1 < llfll-llzll/X 1, llAzll < llf ll. Тогда (Df,f) < Л llf ll2 при Л = y + o + 1 /X 1, то есть максимальное собственное значение D не превосходит Л. Уравнение вида Df = У равносильно системе

Y ( f - f a ,g ) + ( Q * ( BQf - U),g ) =

Z t + Az = f, z l t =о = 0 ,

• - q t + Aq = Bz, q \ t = t = 0 ,

Yf + q = y, где функции z и q равны нулю на концах отрезка [0,L]. Для её решения воспользуемся методом простой итерации:

z tn ) + Az ⁽ n ) = f ⁽ n ) , z ⁽ n ) | t = ₀ = 0 , - q tn ) + Aq ⁽ n ) = Bz ⁽ n ) , q ⁽ n ) | t = T = 0 , f ⁽ n +1) = f ⁽ n ) - в ( Yf ⁽ n ) + q ⁽ n ) - y ) .

В [21] показано, что итерационный процесс будет сходящимся, если в G (0 , 2 / Л). Поэтому можно взять в = 2Л .

Пусть т = T/K — шаг сетки по времени, будем обозначать верхним индексом k функции, относящиеся к моменту t = t k = кт . Для решения задач вида (10) и (11) воспользуемся неявными конечноразностными схемами:

u ^k -

и к — 1

----+ Au k = f ^к ,

τ

u ^k (0) = u ^k ( L ) = 0 ,

к = 1, ..., K, и0 = uо(x), qk — qk+1

τ

+ Aq k = g^k,

q k (0) = q ^k ( L ) = 0 ,

к = K - 1 , ..., 0 , q ^K =0 .

На каждом временном слое все функции раскладываются в ряд Фурье по системе { w n ( x ) } . Поскольку оператор M заменяется своим конечноразностным аналогом M ^τ , то полезно уточнить его собственные значения, непосредственно вычислив функции M ^т w n , n = 1 ,N .

IV. Заключение

В настоящей работе предложена процедура ассимиляции данных наблюдений такая, что функционал стоимости минимизируется на множестве управлений, при которых заданное начальное состояние является точкой минимума. Доказаны существование и единственность решения оптимизационной задачи, вычислены собственные значения основного оператора, входящего в уравнение для управления. Подробно рассмотрен алгоритм численного решения задачи на примере одномерного уравнения теплопроводности. Полученные результаты могут быть использованы на практике для вариационной ассимиляции данных наблюдений в линейных моделях и в моделях с малой нелинейностью.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009--2013 годы, АВЦП «Развитие научного потенциала высшей школы» (проект 2.1.1-500) и РФФИ (проект 09-01-00284-а).