Задача об оптимальном экономическом росте

Инновационные технологии, научно-технический прогресс, автоматизация производства являются значительным фундаментом высоких темпов роста экономики в длительном периоде. Таким образом, становится актуальным использование моделей экономического роста.

Актуальность проблемы обусловлена тем, что в современной экономике часто используются оптимизационные методы, составляющие основу математического программирования. Грамотное потребление ресурсов имеет огромное значение, поскольку их оптимизация может увеличить прибыль [1].

Постановка задачи. Задача об оптимальном экономическом росте представляет собой задачу о выборе оптимальных траекторий c(t), k(t) для которых благосостояние максимально. Она имеет следующий вид [2]:

^2

= J е-^ИО)* . max, t1

dk

• ■77 = f (k) — Ak — c, dt

kttj = k 1 , 0 <  c(t) <  f (k) где k 1 , A, 8 - заданные числа, a f(k), U(c) - заданные функции.

Решением задачи оптимизации является траектория потребления на единицу эффективного труда {c(t)} и траектория капиталовооруженности эффективного трудa{k(t)}, вдоль которых функционал /(c) достигает максимума. Решение зависит от двух функций: функции полезности U и производственной функции k(t), от трех параметров: нормы дисконтирования, нормы амортизации, темпа рабочей силы и от начального значения капиталовооруженности рабочего. Задача оптимизации может решаться на основе принципа максимума Понтрягина.

Требуется оптимизировать уровень потребления сельскохозяйственного предприятия «Продовольствие», которое занимается выработкой молочной продукции. Имеются данные за 2004 – 2018 гг. о выручке от продажи сельскохозяйственной продукции, о среднегодовой стоимости основных средств и о численности персонала.

Описание алгоритма решения задачи.

• 1)    Построение производственной функция f(k) на основе данных о динамике выпуска продукции и производственных факторах (капитал, труд);

• 2)    Выбор функции полезности U (c);

• 3)    Вычисление точки рaвновесия(k * , c * ), соответствующей сбалансированному росту;

• 4)    Решение системы двух дифференциальных уравнений;

• 5)    Построение траекторий потребления и капиталовооруженности;

• 6)    Вычисление значения функционала для нахождения оптимального уровня потребления.

Решение задачи. На основе исходных данных таблицы 1 построим производственную функцию, которая характеризует объем выпуска продукции, величина которого зависит от затрат факторов производства.

Таблица 1

Экономические показатели предприятия

Год	Выручка от продажи сельскохозяйственной продукции, тыс. руб., Y	Среднегодовая стоимость основных средств, тыс. руб., K	Численность персонала, L
2004	843750	195000	533
2005	860625	210000	540
2006	904500	240000	530
2007	968625	270000	597
2008	995625	285000	543
2009	1046250	288000	535
2010	1113750	300000	570
2011	1181250	330000	600
2012	1215000	360000	615
2013	12048750	375000	630
2014	1282500	382500	628
2015	1333125	390000	637
2016	1390601	409590	676
2017	1380500	410000	650
2018	1367218	405967	670

Производственная функция у = f (k) должна удовлетворять условиям [3; 4]:

f(k) > 0,/(к) > 0,f" (к) <0 V к>0,

/(0) = 0,/'(0) = ^.

В результате обработки данных, используя программу Microsoft Excel, был построен график производственной функции за данный промежуток времени. С помощью аппроксимации найдена математическую модель, которая наилучшим образом описывает наблюдаемые значения. Найденная функция имеет вид:

у = 1506,1k0,123.

Эта функция удовлетворяет условиям:

/(к) = 1506,1к ⁰ , ¹²³ > 0, / ' (к) = 185,2503к ^-0 , ⁸⁷⁷ > 0, / '' ^(fe) = -162,4645к ^-1 , ⁸⁷⁷ < 0, /(0) = 1506,1 * 0 ⁰ , ¹²³ = 0, / ' (0) = 185,2503 * 0 ^-0 , ⁸⁷⁷ = от.

Примем, что функция полезности имеет вид:

7(c) = vc,

где c(t) - потребление, которое приходится на одну рабочую единицу.

Данная функция так же удовлетворяет требуемым условиям:

/7(c) = Vc > 0,

7 ' (c) =

> 0,

2 7 '' (c) = - —= <0,

1 t/'(0) = —=«.

3V0

Начальные условия: t 1 = 0, t₂ = 14. Коэффициент амортизации капитала /х = 0,06.

Годовой темп прироста числа занятых п составляет 0,016. Норма дисконтирования 3 = 0,5.

Найдем стационарные траектории c * = const, к * = const.

к* получим из уравнения: / ' (к * ) =/ + п + 3:

185,2503к * ^-0,877 = 0,06 + 0,016 + 0,5,

к* = 722,76.

Вычислим c * = /(к * ) -(/ + п)к * .

c * = 15 0 6,1 * 7 2 2,76 ⁰ , ¹²³ - (0,06 + 0,0 1 6) * 7 2 2,76 c * = 3329,69.

Величиные к*, c* удовлетворяют неравенству:   0 < c* < /(к*).   Точка равновесия (к*, c*) является траекторией сбалансированного роста.

Вычислим значение функционала / (c):

14                                       14

/(c) = J _e ^-0 ,5 ⁽ t ^-0) * ^3329,69^3 = 14,9^ e ^-0 , ^5t dt =

= 14,9(—-е " ⁷ +-е ⁰ ) = 29,84.

\  0,5         0,5   /

Полагая

/ = 0,06, п = 0,016,3 = 0,5, методом Рунге-Кутта 4 порядка вычислим решение системы дифференциальных уравнений

cc = -^(f (к) — ц — n — 8)c, { к = f(k) — (ц + n)k — c.

Показатели потребления и капиталовооруженности имеют тенденцию роста, но потребление растет значительно быстрее, чем капиталовооруженность. Значение функционала J(c) при этом равно 29,84.

График траектории потребления на рисунке 1 изображен линией зеленого цвета, график капиталовооруженности – линией синего цвета.

□

^ Project

Построить траектории

J =

29,837909823

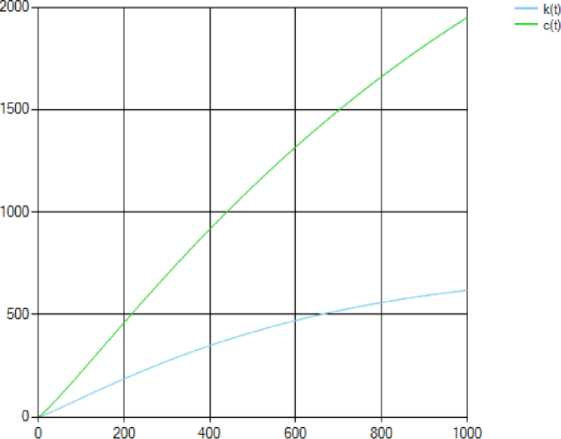
Рис. 1. Траектории потребления и капиталовооружённости.

Вычислить функционал

Увеличим коэффициент амортизации ц до 0,3 и посмотрим на поведение модели. Решим систему уравнений с параметрами:

ц = 0,03, п = 0,016, 8 = 0,5.

Полученные результаты показывают, увеличение коэффициента амортизации капитала незначительно замедляет рост потребления и капиталовооруженности. Только в случае уменьшения уровня инфляции можно добиться роста капиталовооруженности. Значение функционала в данном случае равно 29,04.

Теперь рассмотрим модель при уменьшении нормы дисконтирования. Начальные условия: t 1 = 0,t₂ = 14, ц = 0,06, n = 0,016, 8 == 0,03.

Полученные результаты показывают, что в данной ситуации наблюдается рост как траектории потребления на единицу эффективного труда, так и траектории капиталовооруженности эффективного труда. Следовательно, уменьшение нормы амортизации увеличивает скорость роста обеих величин, что говорит о важности долгосрочного планирования. При данных параметрах значение функционала равно 180,14.

Вывод. Таким образом, в результате проделанной работы поставленная цель была достигнута, а именно: разработана экономико-математическая модель и выполнена оптимизация уровня потребления для экономического объекта. На основе принципа максимума решена задача оптимизации сбережений. Получены оптимальные траектории потребления и капиталовооруженности. Анализ полученных результатов позволяет сделать вывод о том, что максимизация потребления происходит в том случае, когда норма дисконтирования будет минимальной.