Задача об устойчивости круговых колец, связанных между собой

От работ Эйлера по теории продольного изгиба берет свое начало теория устойчивости упругих систем. Задачи упругой устойчивости в классическом случае сводятся к отысканию и исследованию точек бифуркации нелинейных уравнений равновесия. Линеаризация этих уравнений приводит к некоторой линейной краевой задаче на собственные значения. Современное состояние теории упругой устойчивости изложено в монографии [1]. Задачи устойчивости круговых арок и колец, находящихся под действием равномерного давления, подробно изложены в работах [2, 3]. Исследования в области устойчивости арок не прекращаются и в настоящее время [4]. При потере устойчивости колец и арок происходит либо плоская деформация (все перемещения происходят в плоскости неде-формированного кольца), либо пространственная (перемещение перпендикулярно плоскости кольца, и присутствует кручение). Но в случае, когда кольца связаны друг с другом, при потере устойчивости возникают перемеще-

The problem of the stability of circular rings connected to each other

V.Yu. Andryukova, V.N. Tarasov

Institute of Physics and Mathematics,

Federal Research Centre Komi Science Centre, Ural Branch, RAS, Syktyvkar

The paper considers the problems on the stability of a system of circular rings interconnected in such a way that the displacements of these rings and the rotation angles of their sections coincide at some points. This problem is reduced to some variational problem with restrictions on the desired functions in the form of linear equations. The Fourier series are used for a finite-dimensional approximation. The paper also presents the problem on the stability of a system of circular rings reinforced with inextensible threads that do not withstand compressive forces. In this case, there are constraints in the form of inequalities, and after a finite-dimensional approximation, the problem is reduced to finding bifurcation points for nonlinear programming problems in the presence of constraints in the form of inequalities.

Если давление достаточно велико, то первоначальная круговая форма становится неустойчивой, и арка принимает другую, нетривиальную форму. Предположим, что нагрузка P постоянно направлена к центру кривизны. В этом случае работа внешних сил равна W = PRW , где

W (u,w,v,Y) =

π

I/ (2и2

- π

— и’2 — v‘2 + v2) d^. (4)

1. Пространственная деформация круговых арок

В положении равновесия функционал полной энергии

Пусть тонкий упругий стержень, представляющий собой кольцо радиуса R , находится в равновесии, силы равномерно распределены по его длине. Предполагается, что сечение стержня постоянно, и одна из главных осей инерции поперечного сечения лежит в плоскости дуги. В некоторой точке M ₀ проведем три взаимно перпендикулярные оси ( х 0 , у 0 , z 0 ) : ось у 0 направлена по одной из главных осей инерции сечения, перпендикулярного плоскости дуги, ось x ₀ , соответственно, направлена к центру кривизны дуги, ось z ₀ — по касательной к дуге стержня. Пусть в результате деформации стержня оси ( х 0 , у 0 , z 0 ) переходят в оси ( х, у, z ) , точка M 0 переходит в точку M , проекции перемещений точки M ₀ на оси ( х 0 , у 0 , z 0 ) обозначим через u, w, v . Система координат ( х, у, z ) получается из системы ( х 0 , у 0 , z 0 ) путем переноса и путем поворота вокруг осей ( х 0 , у 0 , z 0 ) на углы а, в, Y ■ Считая деформации малыми, можем написать уравнения Клебша [1]:

J(и, w, v,Y) = U

α1

—W=2 / R2(u"+u)2+

α0

A

⁺ R 2

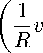
- γ Rdv - W

принимает минимальное значение. В (5) A, B, C — упругие постоянные. Система уравнений Эйлера для функционала (5) распадается на две независимые подсистемы (6) и (7)

R3 (uIV + I и’’ + и) + P (и’’ + и) = 0,     (6)

A i A i C i C i

R3 v () — R2 Y — R3 v — R2Y + P(v + v) = 0 •

в = du + 1 w, ds R dv

^A i

R3v

-

A i     C i      C i

R2 Y + R2 v + RY =0.

—а =

dw

-ds

ds ,

Ru=0 •

где ds = Rd^, ^ G [ —п,п ] — центральный угол дуги стержня. Третье уравнение выражает условие несжимаемости оси стержня.

Упругая энергия стержня в результате деформации определяется формулой

U =

α1

2 I(Ap

α0

+ BSq2 + CSr 2) Rd«,

Это означает, что при потере устойчивости происходит либо плоская деформация, при которой v = 0 , y = 0 , либо пространственная ( и = 0 , w = 0 ).

Для определения критического давления требуется найти минимальное значение силы P , при котором задача на минимум функционала (5), или, что то же самое, система дифференциальных уравнений (6) или (7), имеет нетривиальное решение. Очевидно, последняя задача эквивалентна вариационной проблеме изопериметрического типа

J ^ min при ограничении W = 1 . (8)

где A, B — жесткости стержня на изгиб, C — жесткость стержня при кручении.

Функции и, w, v, y должны быть I п -периодическими. Используя ряды Фурье, получим значения критической силы:

— в случае плоской деформации ( v = 0 , y = 0 )

[ sp = R(а + y) = R (—R v‘+ y),

< Sq = Rв’ = R2 (U‘ + u),                 (3)

[ sr = R(y — а) = R (Y + R v‘) ,

P1 = 4.5 B3,                   (9)

— в пространственном случае ( и = 0 , v = 0 )

где штрих обозначает производную по ϑ .

Предположим, что кольцо нагружено давлением P , равномерно распределенным по его оси. При любой величине давления возможна круговая (первоначальная) форма равновесия.

= A _1|_

2 R3 4+ A .

Эти результаты содержаться в работе [2]. Критическая сила будет равна минимальному из чисел P 1 и P 2 .

2. Задача устойчивости системы круговых колец с неудерживающими связями. Пространственный случай

Рассмотрим систему, состоящую из m круговых колец, координаты которых в недеформированном состоянии описываются уравнениями

{ x * = R sin $ cos ф * , y ⁰ = R sin $ sin ф * ,                (11)

z* = R cos $,

где i = 1,. ..,m, ф* G n(*- 1), $ G [—п,п ].

Введем следующие обозначения: n * = ( — sin $ cos ф * , — sin $ sin ф _i , — cos $ ) — вектор единичной нормали к кривой, определяемой уравнениями (1), т *   =

(cos $ cos ф * , cos $ sin ф _i , — sin $ ) — касательный вектор, b i = T i x n * = ( — sin ф _i , cos ф _i , 0) — бинормаль, u * ( $ ) , w * ( $ ) , v * ( $ ) , i = 1 ,... ,m — перемещения точек i -того кольца вдоль n _i , τ _i , b _i , соответственно, в результате деформации. Предположим, что каждая арка нагружена давлением P , которое остается направленным к центру кривизны (центру сферической поверхности). В результате деформации упругая энергия системы может быть вычислена по формуле [2]

кольца, связанные между собой при $ = 0 и $ = —п .

Для того, чтобы перемещения колец совпадали, должны выполняться равенства:

при $ = 0

w1 =

w1 =

при $ =

w1 =

w1 =

2 w 2

—

—

2 w 3

—п

—

2 w 2

—

у v 2,

—

—

v 1 = у w 2

3 у v3,

V1 = у w 3

у v 2,

v 1 = — у w 2

+

—

+

2 v2 ’

2 v 3 ’

2 v2 ’

u 1

u 1

u 1

= u 2.

= u з;

= u 3.

m

U = EU. = i=1

π

2 у (A*5p2 + B^q* + C^)d$,

2 w 3

+ y v3,

- π

v 1 = —27 w 3

—

2 v 3 ’

u 1

= u3.

где A _i , B _i — жесткости стержней на изгиб, C _i — жесткость при кручении.

;            1 " , 1

5p* = — Rv* + R*'

.                ¹ / ‘‘ .

§q* = — R2(u*+ u*),

1 *       1

5r* = — ry* + R2 v‘.

Для совпадения углов поворота необходимо потребовать выполнения равенств:

при $ = 0

a1 = a2,

2 Y 2 + у в 2 = Y1,

—

— Y 2 + 2 в 2 = в 1;

Углы поворота определяются формулами

a1 = a3,

—

a* = —1 v‘,  в* = 1( u* + w*),

RR

2 Y 3

—

3«

у в 3 = Y1,

—

и выполнено условие несжимаемости u * = w ‘ . В случае центральной нагрузки с учетом условия несжимаемости работа внешних сил определяется формулой

при $ = —п

Т ^{Y 3}

—

2 в 3 = в i;

π

W* = 2 У (u*2

- π

a1 = a2,

2 Y 2

—

3fi

-у ^в 2 = Y 1 ,

— 2 w2 + v*2 — v2) d$,

— Y 2 + 2 в 2 = в 1;

m

W = X W*

i =1

a1 = a3,

—

2 Y 3

—

3R у в 3 = Y1,

Полная энергия системы колец имеет вид

mm

J = X J* = X (u* — у • W* i=1       i=1

Т ^{Y 3}

—

2 в 3 = в i.

Для определенности положим m = 3 , т.е. имеется три

Представим себе, что каждое кольцо подкреплено нерастяжимыми нитями так, что расстояние между точками прикрепления нити к кольцу не может увеличиваться. Пусть

концы j -ой нити прикреплены к кольцу, соответствующему углам $ = б 1 и $ = б 2 , б 1 и б 2 зависят от j . Обозначим u i = u i ( 6 j ) , w i = w i ( 6 j ) , v i = v i ( 6 j ) . Тогда координаты точек кольца в некоторой неподвижной системе координат определяются формулами

{6i = (R — ui) cos 6j — wi sin 6j, ni = (R — ui) sin 6j — wi cos 6j,        (23)

S i = v i ,

( n C j , z ) <  0 , j = 1 . . . , m 0 .

Обозначим через Г конус, определяемый ограничениями (29)–(30). Для решения экстремальной задачи (27)–(30) применяется метод последовательных приближений: пусть z0 ∈ Rn — некоторое начальное приближение. Пусть уже получена такая точка zk G Rn, что g(zk) = 1. Введем множество Mk = {z G Г| (Qz0, z — z0) = 0}. Найдем точку zk+1 G Mk, такую, что где j = 1,2. Расстояние между точками прикрепления нити равно

f ⁽ z k +1 ) = min f ⁽ z ) . z ∈ M k

Р = Р ( u 1 ,w 1 ,V 1 ,u 2 ,w 2 ,V 2 ) =

= V ( C 1 ^— C 2 ) 2 ⁺ ( n 1 ^— n 2 ^{) 2 +} ( ^Z 1 ^{— Z} 2 ^{) 2} .

Обозначим через p 0 = p (0 , 0 , 0 , 0 , 0 , 0) . Деформации кольца должны удовлетворять неравенству

ρ ≤ ρ 0 .                      (24)

Подставляя (23) в (24) и используя разложение в ряд Тейлора с точностью до линейных слагаемых, вместо (24) получим линейное неравенство

(cos ш — 1)( u 1 + u 2 ) + sin ш ( w 1 — w 2 ) <  0 ,   (25)

в котором u 1 = u 1 ( j ) , w i = w i ( j ) , где j — номер нити, ш = б 2 — б 1 . Функции w i , v i , Y i будем искать в виде рядов Фурье:

n wi = ^2 aki cos k$ + bki sin k$, k=2

n ui = ^2 —akik sin k$ + bki cos k$, k=2

n vi = ^2 Cki cos k$ + dki sin k$, k=2

n

Y i = P^ C ki cos k$ + d ki sin k$.

k =2

Пусть z G RN — вектор коэффициентов в (26), N = 6n x 3. Подставляя (26) в (12), (13), получим две квадратичные формы f (z) = 2 (Gz,z) и g(z) = 2 (Qz,z) соответственно. Равенства (15)–(22) дают 24 линейных ограничения вида (nj ,z) = 0, j = 1,..., 24. Наконец, неравенства (25) дают ограничения вида (nj , z) < 0, j = 1... ,m0, где m0 — число подкрепляющих нитей. Таким образом, для определения критической нагрузки получаем задачу нелинейного программирования f (z) ^ |(Gz, z) ^ min при ограничениях g (z ) = |(Qz,z) = 1,(28)

(n3 ,z) = 0, 3 = 1..., 24,(29)

Далее полагаем zk+1 = TTzk +1, где Sk = Vf (zk+1).

S k

Можно показать, что f ( z _k ) монотонно убывает, и последовательность {z k } сходится к некоторой точке z ∗ , в которой выполнены необходимые условия экстремума (теорема Куна-Таккера).

3. Результаты численных экспериментов

Предполагается, что сечение всех колец представляет собой эллипс с полуосями a и b . Тогда жесткости при изгибе и жесткость на кручение могут быть вычислены по формуле

A = ^ПЕа ³ b, B = ^ПЕЬ ³ a, 44

4 AB

EA + B'

В последних выражениях E — модуль Юнга, который без ограничения общности можно положить равным единице. Также можно считать, что R = 1 .

Обозначим через P 0 = min( P 1 , P ₂ ) . Пусть P — значение, полученное в результате решения задачи оптимизации (27)-(29). Тогда при a < b отношение P— = 1 . 35 . Если же a >  1 . 5 b , то —— 0 = 1 . 3968 . В случае 1 <  a <  1 . 5 , отношение _P ^P ₀ возрастает от значения 1.35 до 1.3968. Если же каждое кольцо подкреплено нитями, расположенными по сторонам правильного M -угольника, то значение критической нагрузки зависит от M . Некоторые результаты при

a

= 2 . 5 , b = 1 приведены в таблице.

Зависимость критической нагрузки от числа подкрепляющих нитей Dependence of the critical load on number of reinforcing threads

M	4	5	6	7	8	9
P/P 0	2.89	2.91	2.59	4.08	3.94	3.94

Заключение

В работе рассмотрена задача устойчивости системы упругих колец, подкрепленных нерастяжимыми нитями. Данная задача является конструктивно–нелинейной, так как уравнения равновесия не могут быть линеаризованы в связи с тем, что содержат негладкие функции. Исследована проблема поиска точек бифуркации решения некоторой задачи нелинейного программирования при наличии ограничений в виде неравенств. Численные расчеты показали, что односторонние (неудерживающие) связи существенно увеличивают критическую нагрузку даже при небольшом количестве колец и нитей. Результаты работы могут оказаться полезными при проектировании сетчатых оболочек и арочных систем.