Задача оптимальной стабилизации линейных многосвязных биомедицинских динамических систем

А. В. Щенников, В. Н. Щенников

Приводится формулировка задачи оптимальной стабилизации линейных многосвязных биомедицинских систем с перекрывающимися декомпозициями и разбирается метод ее решения.

Отличительной особенностью многосвязной эргатической управляемой динамической системы является ее большая размерность. Большая размерность систем приводит к серьезным трудностям как аналитического, так и вычислительного характера. Особенно это касается эргатропных управляемых динамических биомедицинских систем. К указанным моделям относятся, например, модели, описывающие взаимодействие посредством диффузии через мембрану одинаковых клеток [3]. В дальнейшем будем считать, что рассматриваемые здесь модели описываются многосвязными линейными системами обыкновенных дифференциальных уравнений с перекрывающимися декомпозициями (подсистемами). Известно, что субоптимальная стабилизация не приводит к оптимальному управлению, а врач-оператор должен иметь точный результат [2]. В этой связи в данном исследовании и разрабатывается способ решения задачи оптимальной стабилизации применительно к указанным системам, т. е. к системам

( _{S 11}

+ B ₂1

_v ⁵ 31

⁵ 32 J

U 1

М 2

Пунктирными линиями здесь обозначены перекрывающиеся подсистемы. Вектор х представим в виде x = ( x f , x^f , x^f ) , где x _Y е В ” ¹, х ₂ е В ” ², д₃ е В ” ³, ”_ + и₂ + и₃ = и, а вектор управления — в виде и = ^ u^f, и₂ ) , и ^ е В ™ ¹ , U 2 е В ™ ² , m i + m 2 = т , т <  и . Далее из трех компонент вектора х образуем две

dx_v "  ^dt dx 2

dt ^dx 3

( dt v

_c ⁴ 31

, ⁴12; ⁴ 13

; ⁴22 ; ⁴ 23

I ⁴ 32 ⁴ 33 _v

x ₁ ^x 2

c ^X 3 j

компоненты ^₁ = ( x^f, x^f ) , у _г = ( x^f , x^f ) . Тогда получим новый вектор у = ( y^f, y^f ) ■ Вектор у связан с вектором х соотношением у = Уд. Размерности постоянных матриц A_s j , (s,j = 1,3), и B_si, ( s = 1,3, i = 1,2) соответствуют размерностям соответствующих векторов х , и « г .

Выберем U, У,и М в виде [2, с. 458 — 459]

( Л

U = 0

1 ^2

2 2

0    0 5

1 ^2

2 2

4 )

м =

fк о о 1

О /2 о о /2 О к о О /3 J

уровне, s = 1,2. С учетом принятых обозначений система (2) будет иметь вид

1 .

2 ^ 22

1 „

” 2 ^А 22

1 .

” 2 ^А 32

1 .J

■ 2 А12

“ 2 А22

1А22О

2 Аз2О

ddi dt dy2 dt где

= ^А 1 # 1 + ^В 1 ^м Л + ^А 12 # 2 + ^В 12 ^м Г к

= ^А 2 У 2 + ^ВВ 2 ^м Л ^{+ А} 21 ^ 1 + ^В 21 ^мГк

(2.2)

^А 1 =

^А 11   ^А 12 ^{1         f А} 22 ^А 23)

I ,      а 2 = I                    I ,

. ^А21 ^А 22 J         к ^А 32 ^А 33 J

~    (В-В*)*)

ВИ

=

1 D ’ к В217

есть матрицы, соответствующие двум подсистемам

и, считая, что N =0, получим систему с непе-рекрывающимися декомпозициями (подсистемами), т. е.

d^ t dt ^d № к dt )

f ^АИ ^А 12 ' ⁰

^А 21 ^А 22 ! ⁰

^{А 21 0 А 22} к ^А 31 ⁰ | ^А32

^А 13

^А 23

^А 23

^ = .4!^! + Й.^^, at (3.1) ddt: = А'2У'2 + ВВ2мЛ2' (3.2) fо А13I к 0 А23 J

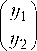
^А 21

^А 21

^А 31

^А 33

Здесь

^А 12

01 ’

' 5 11 ! 5 12' ^ ^{5 22 5 21} ; ^{5 22}

1 5 з1 i 5 32 J

(2.1)

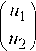
В 12

^В 12

^В 22

В 21

В 21

^В 31

являются матри

Здесь N = В - VB , В и В — матрицы по

стоянные, являющиеся множителями при м = ( «1, М2 /' соответственно систем (1) и (2).

Обозначим через м

(0 _( ( ^s) 7 (0 / ) л = I ^ ^м 1л ^ , ^ ^м 2л ) I

т

управления на локальном уровне, а через

т

МГs) = ^(М1Г ) - (м2г) I

на глобальном

цами связей. Задача решается в два этапа. На первом этапе системы (3.1) и (3.2) в предположении их управляемости строятся модальные стабилизирующие системы (3.1) и (3.2). На втором этапе, т. е. на глобальном уровне, решается задача оптимальной стабилизации с учетом того, что подсистемы (3.1) и (3.2) асимптотически устойчивы. На этом этапе строится и функционал качества управления. В заключении приводятся решения конкретных задач. Данное исследование продолжает и развивает исследования, содержащиеся в работах [1—3].