Задача оптимизации сжатой цилиндрической оболочки с учетом ее надежности

Оптимальное проектирование конструкций из полимерных композиционных материалов (ПКМ) является актуальным вопросом в механике деформированного твердого тела. Под оптимальным проектированием принято понимать установление таких характеристик конструкции, несущей заданные нагрузки, при которых она по определенному критерию будет наилучшей из всех возможных вариантов.

Механические характеристики ПКМ, обусловливаемые свойствами компонентов и схемой расположения армирующих волокон, могут изменяться в широких пределах, что позволяет получать оптимальные в весовом отношении конструкции с заранее заданной анизотропией механических свойств, соответствующей характеру действующих нагрузок.

Анализ условий и методов решения задач оптимизации цилиндрических оболочек из полимерных композиционных материалов. В качестве параметров оптимизации принимаются направления армирования волокон, интенсивность армирования в заданном направлении, соотношение арматуры и связующего в ПКМ, геометрические размеры оболочки и т. д.

В зависимости от условий эксплуатации оболочки из ПКМ в качестве критерия оптимизации или физических ограничений могут быть взяты минимальный вес конструкции при условии обеспечения прочности и устойчивости, максимальная надежность конструкции, максимальная жесткость конструкции с учетом фактора времени, максимальная частота первой формы собственных колебаний при динамическом нагружении и другие характеристики и свойства оболочки из ПКМ.

Критерий минимума веса наиболее часто применяется при проектировании конструкций летательных аппаратов. Задача минимизации веса цилиндрической оболочки из ПКМ решается методом нелинейного програ-мирования или методом множителей Лагранжа. Трудности задач оптимального проектирования цилиндрической оболочки из ПКМ состоят в составлении функций ограничений и в сложном виде таких задач.

Расчет оптимальных параметров цилиндрической оболочки из полимерных композиционных материалов, нагруженной осевой сжимающей силой. Ставится задача спроектировать цилиндрическую оболочку из ПКМ так, чтобы оболочка имела наименьший вес G, выдерживая при этом заданную нагрузку N при заданной длине L .

Требуемые механические характеристики и свойства оболочки из ПКМ определяются действием осевого сжимающего усилия N. Так, должно выполняться условие прочности материала. Кроме того, при исследовании несущей способности тонкостенной оболочки, наряду с прочностью, должна быть обеспечена достаточная устойчивость. Известно, что тонкостенные оболочки под действием критических величин сжимающих напряжений, далеко не достигающих пределов прочности, искривляются и этот процесс заканчивается либо разрушением, либо развитием больших деформаций, нарушающих работу отдельного элемента или всей конструкции. В нашем случае необходимо учитывать возможность как местной потери устойчивости оболочки, так и потери ее устойчивости в целом как трубчатого стержня с кольцевым сечением.

Оптимальная степень наполнения углепластика находится в пределах 57.. .63 %, что соответствует объемному модулю армирования р = 0,57...0,63 . Этот же результат получен при решении задачи оптимизации цилиндрической оболочки при внешнем давлении и осевом сжатии в работе (рис. 1).

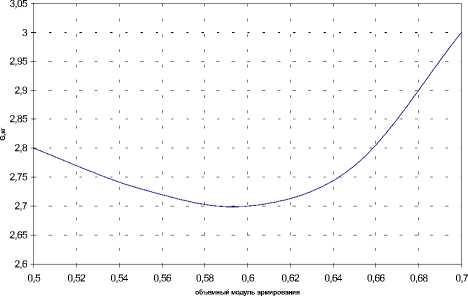
Рис. 1. Зависимость веса сжатой оболочки от объемного модуля армирования ПКМ %

Таким образом, в задаче оптимального проектирования можно принять следующие оптимальные параметры цилиндрической оболочки из ПКМ, работающей в условиях осевого сжатия:

• -    объемный модуль армирования р = 0,6 ;

• -    армирующие слои направлены под углами ф ₀ = 0°, ф ₄₅ = ±45° , ф ₉₀ = 90° к продольной оси оболочки;

• -    коэффициенты армирования соответственно равны у ₀ = 0,75; у ₄₅ = 0,22; у ₉₀ = 0,03.

Оптимальная анизотропия ПКМ сжатой цилиндрической оболочки, количество элементарных слоев по толщи-mm m не в котором т >8, имеет вид -0-0- + ± 445 + -909^, где m0 -количество слоев, армированных в продольном направлении, m0 = 0,75m = 6, 7, 8,...; m45 - количество слоев, армированных под углом ± 45°, m45 = 0,22m = 2, 4, 6,...; m90 - количество слоев, армированных в окружном на- правлении m90 = m - m0 - m45 • При количестве слоев т < 8 оптимальная анизотропия материала имеет вид m. Армирование материала в окружном направлении при т < З0 обеспечивается только верхним технологическим слоем.

Современные ПКМ обнаруживают разброс прочности и упругих свойств5 что приводит к необходимости развития статистических подходов к оценке несущей способности конструкций5 изготовленных из этих материалов. Использование статистических методов становится особенно актуальным при проектировании оптимальных конструкций из ПКМ. Проектирование таких конструкций трактуется как проблема обеспечения их надежности при минимальном весе.

Условие неразрушаемости моделей можно записать в виде

данной нагрузке А с вероятностью не менее р оболочка имела наименьший вес G ( x ) .

Задача оптимального проектирования с учетом надежности конструкции сводится к нахождению значений критических усилий при местной N M ( x ) и общей N 0 ( x ) потере устойчивости при разрушении материала N 0 ( x ) :

N 0 M ( x ) = k M ■ 2п- h ² ■ «■ ( Т - Y ■ v M )

N 0 0 ( x ) = k 0 *л* L “² ■ h ■ R ³ ■ E 1 - ( 1 - Y ■ v 0

N 0 ( x ) = k 0 ■ 2n ■ R ■ h ■ 3 ■ ( 1 - Y ■ v ₀ ^R )

k 0 V ( и 1 , U 2 ,

....

, U_r X^1- У ■ ^v 0 ) m = N 0 ⁵

где V ( и 1 , U ₂ ,..., U_г ) - функциональная зависимость расчетной нагрузки от средних значений геометрических характеристик моделей и механических свойств их мате-риала5 определенных при испытании образцов; k ₀ - среднее значение параметра нагрузки принятого в виде отношения предельной нагрузки определенной при испытании моделей5 к ее расчетной величине; v ₀ - коэффициент вариации параметров нагрузки; У- квантиль надежности соответствующий заданному уровню надежности; т - коэффициент условий работы5 учитывающий изменение предельной нагрузки при воздействии некоторой физической среды; N ₀ - эксплуатационная нагрузка. Этот коэффициент принимается в виде произведения отношений нормированных значений параметра нагрузки в фиксированные интервалы времени воздействия среды:

m =^I0F i i v : l - 1 ⁵

_ i ■=1 k 0 ( 1 - У ■ v ₀ )

где k 0 , v 0 - средние значения и коэффициенты вариации параметра нагрузки в i -й момент времени на i -м этапе испытаний; t - общее количество интервалов времени либо этапов испытаний. Особенностью условия неразрушаемости является ТО5 что все случайные свойства моделей сведены к одному обобщенному параметру нагрузки благодаря чему значительно облегчается решение ряда практических задач5 связанных с выбором расчетной зависимости определением коэффициента безопасности и оценкой надежности.

где k M , v M - среднее значение и коэффициент вариации параметра нагрузки при местной потере устойчивости оболочки; k 0 , v 0 - среднее значение и коэффициент вариации параметра нагрузки при общей потере устойчивости оболочки; k 0 , v 0 - среднее значение и коэффициент вариации параметра нагрузки при разрушении материала; У- квантиль надежности соответствующий вероятности р .

Задачу оптимального проектирования будем решать методом множителей Лагранжа.

В целевой функции введем следующие обозначения: A =2 л ■ у ■ L ,

B ^'

= л ³ ■ L "² ■ E 1 ■ k ₀ ⁰ ( 1 -

С = 2 л ■ о 1 ■ k 0 ( 1 - Y ■ v R D = 2 л ■ а ■ k M ( 1 - Y ■ v ₀ ^M

Формула для критической длины оболочки запишется следующим образом:

L =

л ■ а ■ E 1 ■ N [ k ₀ ^э ( 1 - Y ■ v 0

4 ■ о 3 ■

.

Оптимальные размеры h 5 R цилиндрической оболочки выдерживающей осевую нагрузку А с вероятностью не менее р при заданной длине оболочки L 5 имеют следующие значения: г—

- если заданная длина оболочки L = L 5 то

R =

V N ■ D .

C ^'

;

- если заданная длина оболочки L >  L 5 то

R = 6

N ■ D ^'

( вТ

;

- при L <  L размеры h и R могут принимать любые значения5 удовлетворяющие уравнению h ■ R = ^ 5 причем толщина h и радиус срединной поверхности оболочки R ограничены следующими значениями:

Анализ разброса параметра нагрузки позволяет определить коэффициент безопасности при заданной надежности

^в

^в

f =---¹---

1 - Y ■ v 0

n V_ Y j_ v 0_J

•

t

. ■-1

0 D < h < яс Л <  R <  V ND

•

который в общем случае отличается от нормативного коэффициента безопасности f , 5 или надежность конструкции (соответствующий квантиль надежности) при заданном нормативном коэффициенте безопасности:

Y = 7 ^‘ v0

V

f.

I .

Сформулируем задачу оптимизации следующим образом: необходимо выбрать такие толщину оболочки h и радиус поверхности R 5 чтобы при заданной длине L и за-

Средние значения и коэффициенты вариации параметра нагрузки при местной k M , v M и общей k 0 , v 0 потере устойчивости оболочки при разрушении ПКМ k R , v R были определены по результатам испытаний на прочность и устойчивость трубчатых стержней из углепластика КМУ-ЗЛ. Испытания проводились на стержнях длиной 100, 225 и 650 мм5 средним диаметром от ЗО56 до З2 мм и толщиной от O54 до 1^5 мм (рис 2^4).

Полученные средние значения и коэффициенты вариации параметра нагрузки при местной k ₀ ^M, v M и общей k ₀ ^э , v 0 потере устойчивости при разрушении материала

стержней k0R, v0 подчиняются нормальному закону распределения и соответственно равны k0M = 0,60, v0M = 0,08, k0 = 0,88, v 0 = 0,10 ,

Таким образом, полученные выше формулы могут быть использованы для расчета оптимальных размеров, несущей способности и характера ее потери сжатыми стержнями из ПКМ при соотношении 4 <  L / R <  45 .

Размеры и несущая способность стержней с другими параметрами могут быть пересчитаны в соответствии с критериями подобия.

Рис. 3. Характер местной потери устойчивости трубы

Рис. 2. Общая потеря устойчивости трубы

Рис. 4. Характер прочностного разрушения труб от действия осевой сжимающей силы

TASK OF THE OPTIMIZATION OF CABINES CYLINDRICAL CAPSULE WITH ALLOWANCE FOR ITS RELIABILITY

Is decided the task of the optimization of cylindrical capsules, from polymer composite materials with allowancefor their reliability.