Задача оптимизации транспортной схемы

Одной из основных проблем, решаемых транспортной логистикой, является оптимизация маршрутов движения транспортных средств. Многие потребители заказывают со складов партии «меньше чем вагон», «меньше чем трейлер», что значительно увеличивает издержки, связанные с доставкой таких грузов. Для сокращения транспортных расходов склад может организовать унитизацию небольших партий грузов для нескольких клиентов до максимальной загрузки транспортных средств [1].

На рис. 1 в виде направленных графов приведены два примера различных маршрутов обслуживания трех потребителей с одного склада. Здесь рядом с квадратами, изображающими потребителей, указаны их потребности в тоннах, на ребрах графов – соответствующие расстояния.

Пр=44                            Пр=50

1а                                                 1б

Рис. 1. Два варианта прокладки маршрута от склада до трех потребителей

Маршрут от склада до нескольких потребителей с возвратом на склад называется кольцевым маршрутом, если он исключает возможность пересекающихся направлений движения (рис. 1, а ).

Кольцевой маршрут действительно обеспечивает минимальный пробег автомобиля Пр (в данном примере Пр=9+13+14+8=44 км), однако он не учитывает изменение его загруженности по мере объезда потребителей, а следовательно, и общего расхода топлива на маршруте. Естественно, что чем быстрее осуществляется разгрузка автомобиля, тем меньше будет расход топлива на его дальнейшем пути. В данном случае при собственной массе автомобиля, равной 5 т, его товарная масса при кольцевом маршруте составит Тм=8*(5+1+20+5)+14*(1+20+5)+13*(20+5)+9*5=982 т*км.

Для оптимизации транспортных маршрутов обычно решается «задача коммивояжера» [2], в которой исходными данными являются координаты источника (склада) и потребителей, т.е. расстояния от склада до каждого из потребителей и соответствующие расстояния между последними. На рис. 1, б приведена схема маршрута, найденная методом “коммивояжера” [2].

Для вышеприведенных исходных данных эта задача решена нами не по расстояниям, как это рекомендуется в литературе, а по транспортным массам. Это решение показало, что минимальная векторная транспортная масса обеспечивается маршрутом, изображенном на рис. 1, б (Тм=9*(20+5+2+5)+ +7*(5+2+5)+14*(2+5)+20*5=570 т*км.) Это на 42 % меньше, чем при кольцевом маршруте.

Для построения математической модели задачи оптимизации перевозок введем обозначения:

Р i – потребности i -го потребителя, т;

i = 1,…,n – номер потребителя;

• n    – число потребителей;

• j    – номер кольцевого маршрута;

• m    – число маршрутов;

G ам – грузоподъемность автомобиля, т;

V j – средняя скорость автомобиля на j -м маршруте, км/ч;

R j – средний расход топлива на j- м маршруте, л/км.

Тогда математическая модель будет иметь вид:

• -    загрузка автомобиля (т) не должна превышать его грузоподъемности:

k

X Pj ^ GaM         0=1m) ;(1)

i = 1

• -    загрузка автомобиля (т) на каждом маршруте должна быть максимальной:

k

F = X Pi  > Max     (Mm) ;(2)

i = 1

• -    транспортная масса (т*км) должна быть минимальной:

nm

F2 = XX ij ij          .(3)

i = 1 j = 1

Это ограничение на первый взгляд противоречит предыдущему, однако оно выполняется при условии nm

XX ij

i = 1 J = 1

расход топлива (л*ч) за весь производственный цикл должен быть минимален:

m

F 3 = X R j ^ Min .          (5)

J = 1

Расход топлива зависит от марки автомобиля, его загруженности и его средней скорости. Чем выше скорость автомобиля в городских условиях, тем меньше расход топлива. Поэтому после разбиения зоны обслуживания на сектора, одним из приоритетов должно выступать требование максимальной скорости. Это позволит, кроме экономии топлива, уменьшить среднее время ожидания в очереди, а следовательно, определенные преимущества в конкурентной борьбе.

Загруженность автомобиля меняется по мере его движения по маршруту, а следовательно, по мере разгрузки, поэтому целесообразно двигаться сначала к потребителям с наибольшей величиной запросов, с тем, чтобы максимально разгрузить автомобиль, что обеспечит минимизацию расхода топлива на данном рейсе.

На рис. 2 приведен алгоритм решения задачи оптимизации транспортных схем, основанный на использовании улучшенного алгоритма Свира [1, 3] и вышеприведенной математической модели.

Начало

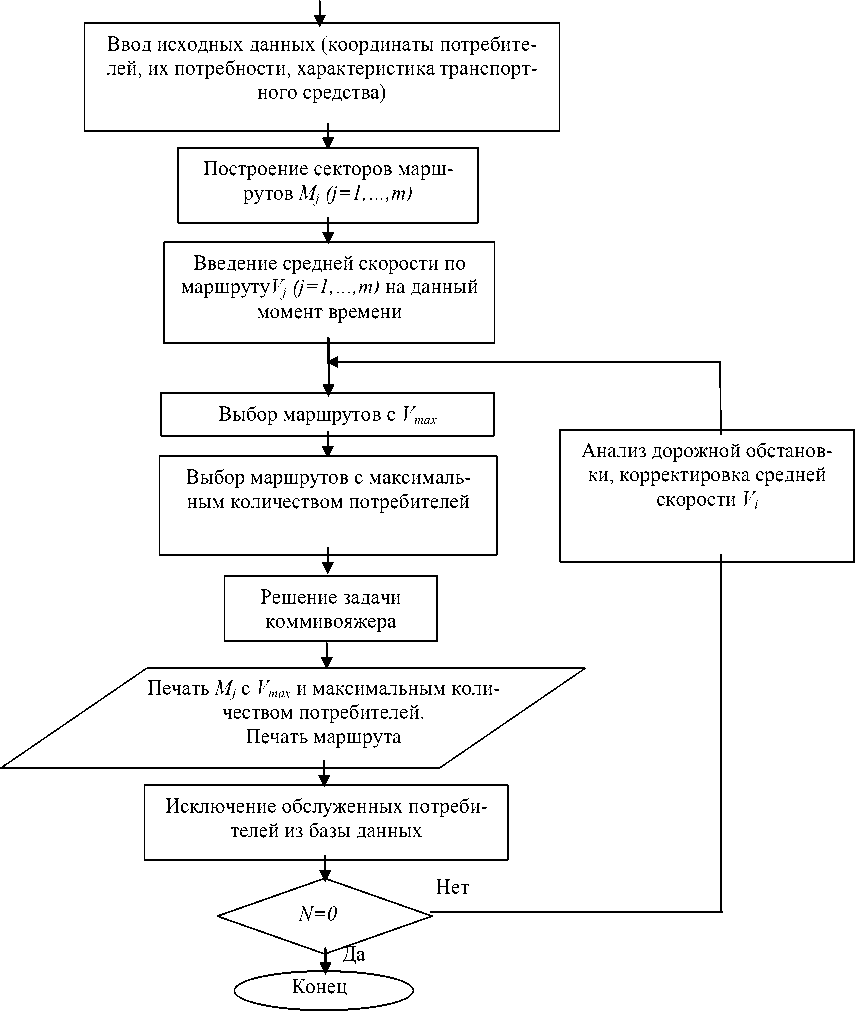
Рис. 2. Алгоритм оптимизации маршрутов перевозок от одного склада

Здесь блок «Построение секторов маршрутов М j (j=1,…,m) » выполняется по разработанному нами ранее алгоритму [3]. Блок «Выбор маршрутов с максимальным количеством потребителей» обеспечивает уменьшение среднего времени ожидания в очереди на поставки.

Дорожная обстановка существенно меняется в зависимости от сезона и в течение суток (часы пик, аварии на дорогах и пр.), поэтому в алгоритм введен блок “Корректировка средней скорости V i ”.

Печать конкретных маршрутов движения транспортных средств обеспечивает водителей конкретной программой их действий. Этот алгоритм был реализован в соответствующих программах, прошедших государственную регистрацию [4, 5].