Задача построения графика работы нескольких передвижных установок

Рассмотрим задачу построения графика работы нескольких передвижных установок, обслуживающих территориально распределенные пункты. Под графиком работы подразумевается время прибытия установки в пункт и продолжительность работы установки в пункте. Передвижение установок осуществляется по транспортной сети, в которой для каждой пары пунктов известно расстояние. Маршрут каждой установки должен начинаться и заканчиваться в заданном пункте, который будем называть базой. В каждый пункт установка должна попасть не позднее заданного времени, опоздания не допускаются. Особенность этой задачи заключается в том, что, прибыв в пункт, установка должна выполнить работу, на которую затрачивается определенное время, причем установки обладают разной производительностью, то есть затрачивают разное время на выполнение одной и той же работы, а также разной стоимостью работы в пункте и стоимостью перемещения из пункта в пункт. Ограничение на выполнение работы отличает рассматриваемую задачу от задачи маршрутизации нескольких коммивояжеров с центральной базой и с временными окнами [1].

Приложением такой задачи является задача определения графика перемещений между несколькими удаленными котельными передвижных рубильных машин для производства щепы энергетического назначения. Известны запасы щепы на начало периода планирования и количество щепы, которое необходимо произвести для обеспечения ежедневных потребностей котельных [3].

В приложении задачи для рубильных машин ничего не говорится о том, сколько раз необходимо посетить каждый пункт. Самый простой вариант предполагает единственное посещение каждого пункта. Построим модель такой задачи.

Пусть M – множество пунктов, тогда m = |M| – количество пунктов; N – множество установок, n = |N| – их количество; T – период планирования; Vk – скорость перемещения установки k; Pk – производительность установки k; Ck – затраты на выполнение единицы работы установкой k; Dk – затраты на перемещение установки k на единицу расстояния; A0i или Ai0 – расстояние от пункта i до базы; Aij – расстояние от пункта i до пункта j; Ti – самое позднее время прибытия установки в пункт i; Wi – объем работы, который необходимо выполнить в пункте i.

Для решения задачи требуется разбить множество пунктов на непересекающиеся подмножества, каждое из которых будет обслуживать одна установка. Кроме этого, необходимо определить маршрут движения каждой установки, который представляет собой упорядоченную последовательность пунктов. Обозначим через H sk подмножество пунктов в разбиении s, обслуживаемых установкой с номером k.

Тогда

n

U Hsk = M и Hsk n Hsr = 0 для k=1

n k Ф r, msk = |Hsk|, k = 1,n, £msk = m.

k = 1

Обозначим через     z sk = ( i sk , i 2k , к , i mk k ) (2)

перестановку элементов множества H sk .    ^s

Введем переменную t j – момент прибытия установки в пункт j.

Задача заключается в определении такого разбиения {Hsk}, перестановок {zsk } для каждого подмножества в разбиении и значений времени прибытия установок в каждый пункт перестановки { zsk }, чтобы выполнялись следующие условия. • Прибытие в пункт должно быть не позднее момента Tj:

tj < Tj, j = 1 ..m.(3)

Прибытие в первый пункт маршрута должно быть равно времени на перемещение установки от базы до первого пункта маршрута:

t sk > A0i^ для msk > 0, k = 1..n.(4)

• •    Прибытие установки в следующий пункт маршрута должно быть позднее момента времени, когда установка выполнит необходимую работу, плюс время на перемещение установки из текущего пункта в следующий пункт:

Wisk     Aiskisk tst +—— +—j- < tsk для msk > 0, k = 1..n. (5) ij      Pk       Vk      ij+1

• •    Прибытие в последний пункт маршрута должно быть не позднее момента времени, когда до окончания периода планирования установка успеет выполнить работу в пункте и вернуться на базу:

W i sk      A i sk 0

t sk +—— + msk— <  T для m_sk > 0, k = 1.. n . (6) i msk      P k      V k

• •    Значения t j должны быть целыми и неотрицательными.                           (7)

Целевая функция минимизирует суммарные по всем установкам затраты на перемещение установки из пункта в пункт согласно маршруту: из последнего пункта маршрута установки к базе, от базы к первому пункту маршрута установки, а также затраты на выполнение работы в каждом пункте:

n                      n                       n m_s k - 1

^ A 0 i s "  D k ⁺ ^ Ai- k^ 0 "  D k ⁺ ^ ^ Ai jk i s^ ' D k ⁺ k = 1                    k = 1      s k = 1 j = 1

n m sk

+ ££ W jk " C_k ^ min.

k = 1 j = 1

Точный алгоритм решения задачи (1)–(8) заключается в переборе всех возможных разбиений множества пунктов и переборе всех возможных перестановок пунктов, входящих в сформированное подмножество H sk – { z^sk }, расчете для них значений переменных t i sk на основе ограничений (4), (5) и проверки выпо ^j лнения условий (3), (6). Блок-схема алгоритма решения задачи (1)–(8) (Алгоритм 1) представлена на рис. 1.

Предложенный алгоритм, обеспечивающий точное решение задачи, имеет высокую вычислительную сложность. Программная реализация алгоритма при небольших размерностях задачи: количестве пунктов менее 13 и количестве установок менее 5, имеет приемлемое время вычисления.

Для большего количества пунктов можно применить модификации эвристических алгоритмов решения задачи коммивояжера, такие как алгоритмы перехода в ближайшую точку, локальной оптимизации, генетические алгоритмы и др. [2], [4].

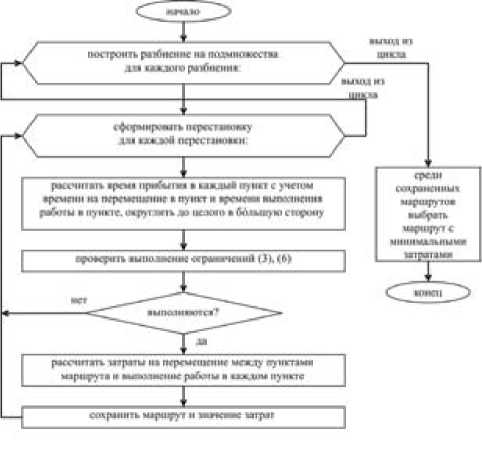
Рис. 1. Блок-схема алгоритма решения задачи без повторных посещений (Алгоритм 1)

Рассмотрим применение алгоритма перехода в ближайшую точку для построенной модели задачи. Суть алгоритма для решения задачи коммивояжера заключается в выборе начального пункта, а затем в последовательном поиске ближайшего пункта по отношению к выбранному на предыдущем шаге. Так как построенная модель отличается от задачи коммивояжера дополнительными условиями, связанными со временем прибытия установки в каждый пункт, под «ближайшим» пунктом будем понимать тот, у которого время наиболее позднего прибытия в него установки является наиболее близким ко времени наиболее позднего прибытия установки в рассматриваемый пункт.

Если рассмотреть задачу, в которой один из пунктов посещается одной и той же установкой дважды, то есть работа в этом пункте выполняется в два этапа, то разумно предположить, что повторный приезд не повлечет за собой дополнительных затрат на выполнение работы, так ее объем не меняется, но может повлечь дополнительные затраты на перемещение установки, кроме случая, когда несколько пунктов связывает одна дорога и перемещение установки в следующий пункт маршрута происходит через ранее уже посещенные пункты, и тогда затраты будут равными. Обоснуем это предположение.

Утверждение. Затраты на перемещение установки при повторном посещении одного из пунктов будут не меньше, чем затраты на перемещение установки без повторного посещения пунктов.

Доказательство. Пусть установка выезжает из пункта 1 и должна возвратиться в пункт 1. Установка должна посетить три пункта: 2, 3, 4. Для каждой пары пунктов определены расстояния между ними, равные aij; и матрица расстояний симметричная. Затраты на перемещение пропор- циональны расстоянию. Иногда между двумя пунктами проходит через третий пункт, в этом случае будем считать, что третий пункт не посещается второй раз, а расстояние между пунктами равно сумме расстояний от каждого из этих пунктов до третьего (например, a12 + a23 = a13).

Итак, пусть, не снижая общности, оптимальный по длине маршрут без повторных посещений соответствует перестановке пунктов (1, 2, 3, 4, 1). Опять же не снижая общности, предположим, что в пункт 2 установка заезжает дважды, тогда возможны четыре варианта оптимального маршрута задачи с повторным посещением.

• 1.    Маршрут в целом совпадает с оптимальным маршрутом без повторного посещения, но между какими-то двумя пунктами вклинивается пункт, посещаемый дважды, например (1, 2, 3, 2, 4, 1).

• 2.    Маршрут в целом совпадает с оптимальным маршрутом без повторного посещения, а повторно посещаемый пункт посещается сразу, например (1, 2, 2, 3, 4, 1).

• 3.    Маршрут полностью меняется, повторно посещаемый пункт посещается не сразу, например (1, 3, 2, 4, 2, 1).

• 4.    Маршрут полностью меняется, повторно посещаемый пункт посещается сразу, например (1, 3, 2, 2, 4, 1).

Для случая 1 расстояние a ₁₂ + a₂₃ + a ₃₂ + + a ₂₄ + а ₄₁ будет больше или равно расстоянию a ₁₂ + a ₂₃ + a 34 + a 41 по правилу треугольника a 32 + a 24 >  a 34 • Следовательно, затраты с повторно посещаемым пунктом будут не меньше.

Для случая 2, так как a 22 = 0, затраты будут такими же, то есть не меньше.

Для случая 3 рассмотрим расстояние a i3 + a 32 + a 24 + a 42 + a 21 >  ^3 + a 32 + a 24 + a 41 по правилу треугольника a ₄₂ + a ₂₁ >  a ₄₁. Далее a ₁₃ + a ₃₂ + a ₂₄ + a ₄₁ >  a ₁₂ + a ₂₃ + a ₃₄ + a ₄₁, так как маршрут (1, 2, 3, 4, 1) является оптимальным, то есть имеющим минимальную длину. Следовательно, a r, + a 32 + a 24 + a 42 + a 21 >  a 12 + a 23 + a 34 + a 41 , тогда затраты с повторно посещаемым пунктом будут не меньше.

Для случая 4 рассмотрим расстояние a13 + a 32 + a 22 + a 24 + a 41 = a13 + a 32 + a 24 + a 41, так как a22 = 0. Далее a13 + a 32 + a 24 + a 41 > a12 + a23 + a34 + a41, так как маршрут (1, 2, 3, 4, 1) является оптимальным, то есть имеющим минимальную     длину.     Следовательно, a^ + a32 + a22 + a24 + a41 > a^ + a23 + a34 + a41, тогда затраты с повторно посещаемым пунктом будут не меньше.

Для случая работы двух установок с различными затратами на перемещение, различными затратами на выполнение работы и различной производительностью в силу ограничений на время прибытия установки в пункт суммарные затраты на перемещение и выполнение работы могут оказаться и меньше при повторном посещении, чем затраты без повторного посещения. В целом же разумно предположить, что затраты начнут возрастать с ростом количества повторно посещаемых пунктов. Однако это предположение требует дальнейшего исследования.

Рассмотрим пример, когда суммарные затраты на перемещение и производство будут меньше в случае с одним повторным посещением, чем затраты без повторных посещений.

Исходные данные задачи включают три пункта и две установки с равными скоростями перемещения и стоимостями перемещения, с равными производительностями, но разными стоимостями работы. Пусть период планирования T составляет всего 14 часов.

Тогда m = 3; n = 2; V 1 = V 2 = 1 км/час; P 1 = P 2 = 1 1/час; D 1 = D 2 = 1 руб./км; C 1 = 1 руб.; C 2 = 0,9 руб.

Поскольку установки обладают равными производительностями, продолжительности работы в каждом пункте для обеих установок совпадают.

Графически расположение пунктов представлено на рис. 2.

Рассмотрим решение задачи для случая по -сещения каждого пункта только один раз. В этом случае количество всех возможных разбиений будет равно 8.

Из таблицы видно, что минимальное значение целевой функции составляет 20,3 руб. Ему соответствует оптимальное решение, включающее два маршрута: маршрут для первой установки – База → Пункт 3 → База, маршрут для второй установки – База → Пункт 1 → Пункт 2 → База.

Рассмотрим решение задачи для случая посещения одного из пунктов повторно. Не будем приводить полный список допустимых решений, приведем два допустимых решения, значения целевой функции на которых будут меньше оптимального значения целевой функции для задачи без повторных посещений.

Матрица расстояний между пунктами и каждым пунктом и базой

	0 – база	Пункт 1	Пункт 2	Пункт 3
0 – база	0	1 км	2 км	3 км
Пункт 1	1 км	0	1 км	2 км
Пункт 2	2 км	1 км	0	1 км
Пункт 3	3 км	2 км	1 км	0

Время прибытия и объем работы
Пункт	Объем работы	Самое позднее время прибытия
1	W 1 = 2	T = 1
2	W 2 = 5	T 2 = 5
3	W 3 = 4	T 3 = 7

Пункт I

Пунш 2

Пункт 3

Прибитое НС

11О1ДНСС. ‘КМ * । час: работа 2 часа

Прибитое нс

работа 5 чааза,

Пробытнс нс ni>uwce, чем • 7 мош. работа 4 часа

Рис. 2. Графическое представление расположения пунктов

Решение 1. Первая установка следует по маршруту: База → Пункт 1 → Пункт 2 → База. В Пункте 2 установка работает только 1 час. Затраты составят: 1 · 1 + 2 · 1 + 1 · 1 + 1 · 1 + 2 · 1 = = 7 руб. Вторая установка следует по маршруту: База → Пункт 2 → Пункт 3 → База. В Пункте 2 установка работает только 4 часа, чтобы не опоздать в Пункт 3. Затраты составят: 2 · 1 + 4 × × 0,9 + 1 · 1 + 4 · 0,9 + 3 · 1 = 13,2 руб.

Суммарные затраты составят: 7 + 13,2 = = 20,2 руб., что на 0,1 руб. меньше, чем оптимальное значение целевой функции для задачи без повторных посещений.

Решение 2. Первая установка следует по маршруту: База → Пункт 2 → База. В Пункте 2 уста- новка работает только 3 часа. Затраты составят: 2 · 1 + 3 · 1 + 2 · 1 = 7 руб. Вторая установка следует по маршруту: База → Пункт 1 → Пункт 2 → Пункт 3 → База. В Пункте 2 установка работает только 2 часа, чтобы не опоздать в Пункт 3. Затраты составят: 1 · 1 + 2 · 0,9 + 1 · 1 + 2 · 0,9 + 1 · 1 + + 4 · 0,9 + 3 · 1 = 13,2 руб.

Суммарные затраты составят: 7 + 13,2 = = 20,2 руб., что на 0,1 руб. меньше, чем оптимальное значение целевой функции для задачи без повторных посещений.

Таким образом, суммарные затраты на перемещение и производство в задаче с одним повторным посещением могут быть меньше, чем суммарные затраты в задаче без повторного посещения.

Допустимые решения задачи без повторных посещений

№ разбиения	Разбиение		Значение целевой функции
	Установка 1	Установка 2
1	{1, 2, 3} Установка не успеет вовремя прийти во все пункты	{ }	Нет решения
2	{1, 2} Маршрут 0→1→2→0: затраты = 1 · 1 + 2 · 1 + 1 · 1 + 5 · 1 + 2 · 1 = = 11; маршрут 0→2→1→0: опоздание в пункт 1	{3} Маршрут 0→3→0: затраты = 3 · 1 + 4 · 0,9 + 3 · 1 = 9,6	Суммарные затраты: 11 + 9,6 = 20,6 руб.
3	{1, 3} Маршрут 0→1→3→0: затраты = 1 · 1 + 2 · 1 + 2 · 1 + 4 · 1 + 3 · 1 = 12; маршрут 0→3→1→0: опоздание в пункт 1	{2} Маршрут 0→2→0: затраты = 2 · 1 + 5 · 0,9 + 2 · 1 = 8,5	Суммарные затраты: 12 + 8,5 = 20,5 руб.
4	{2, 3} Маршрут 0→2→3→0: опоздание в пункт 3; маршрут 0→3→2→0: опоздание в пункт 2	{1} Маршрут 0→1→0: затраты = 1 · 1 + 2 · 0,9 + 1 · 1 = 3,8	Нет решения
5	{ }	{1, 2, 3} Установка не успеет вовремя прийти во все пункты	Нет решения
6	{1} Маршрут 0→1→0: затраты = 1 · 1 + 2 · 1 + 1 · 1 = 4	{2, 3} Маршрут 0→2→3→0: опоздание в пункт 3; маршрут 0→3→2→0: опоздание в пункт 2	Нет решения
7	{2} Маршрут 0→2→0: затраты = 2 · 1 + 5 · 1 + 2 · 1 = 9	{1, 3} Маршрут 0→1→3→0: затраты = 1 · 1 + 2 · 0,9 + 2 · 1 + 4 · 0,9 + + 3 · 1 = 11,4; маршрут 0→3→1→0: опоздание в пункт 1	Суммарные затраты: 9 + 11,4 = 20,4 руб.
8	{3} Маршрут 0→3→0: затраты = 3 · 1 + 4 · 1 + 3 · 1 = 10	{1, 2} Маршрут 0→1→2→0: затраты = 1 · 1 + 2 · 0,9 + 1 · 1 + 5 · 0,9 + + 2 · 1 = 10,3; маршрут 0→2→1→0: опоздание в пункт 1	Суммарные затраты: 10 + 10,3 = 20,3 руб.

Построим математическую модель для задачи, когда дважды посещается только один пункт, причем заранее неизвестно, какой именно. Первое посещение этого пункта должно быть не позднее момента времени T j . Продолжительность первого пребывания в пункте зависит от момента времени второго посещения и должно быть таким, чтобы результатов работы установки при первом посещении хватило до второго посещения, время которого заранее неизвестно и зависит от стоимости работы и стоимости перемещения установки.

Тогда, если H sk – подмножество пунктов в разбиении s, обслуживаемых установкой с номером k , для разбиения s должны выполняться условия:

n

U H sk = M .              (9)

k = 1

Существует единственный пункт j e M , для которого есть два подмножества H_sk и H_sr , такие, что H_sk n H_sr = { j } , для остальных подмножеств выполняется условие:

H sk n H sr = 0 для k + r ,        (10)

если m_S k = | H sk |, k = 1, n , j^ m sk = m + 1. (11) k = 1

Решение задачи (2)–(11) попытаемся свести к решению задачи (1)–(8). Рассмотрим пункт, который посещается дважды, пусть его номер равен j, как два разных пункта (j) и ( m + 1), тем самым увеличится размерность задачи. Расстояния от дополнительного пункта ( m + 1) до всех остальных пунктов совпадают с расстояниями от пункта ( j ) до всех остальных пунктов. Расстояние от пункта ( j ) до пункта ( m + 1) равно нулю.

При фиксированном дополнительном пункте ( m + 1) задача (2)–(11) почти сводится к задаче (1)–(8) с увеличенным на единицу количеством пунктов.

В процессе решения задачи для построенных разбиения и последовательности обхода пунктов (перестановки) необходимо произвести дополнительные расчеты для пунктов ( j ) и ( m + 1) следующих значений: продолжительность пребывания в пункте, объем работы. Эти значения носят динамический характер, так как зависят от технических и экономических характеристик установки и времени прибытия в пункт, поэтому они должны рассчитываться в процессе решения задачи.

Пусть сначала по времени установка приезжает в пункт ( j ), а затем в пункт ( m + 1).

Для приложения задачи к рубильным машинам продолжительность пребывания машины в пункте (j) должна быть такой, чтобы произведенной щепы хватило для работы котельной до следующего посещения, а не на весь период планирования. Продолжительность пребывания в пункте (m + 1) должна быть такой, чтобы хватило щепы до конца периода планирования, плюс требуемый исходный для пункта (j) объем щепы на конец периода планирования, а также не на весь период планирования.

Кроме этого, на продолжительность пребывания в пункте влияет то, какая установка в нем работает. Выгоднее, чтобы дольше работала та установка, стоимость работы которой меньше. Если в пункте ( j ) работает более дорогая установка, то продолжительность работы в этом пункте должна соответствовать наиболее раннему прибытию более дешевой установки в пункт ( m + 1). Если, наоборот, в пункте ( j ) работает более дешевая установка, то продолжительность работы в этом пункте должна быть максимальной, то есть необходимо определить резерв по времени прибытия для пунктов, следующих за посещением пункта ( j ), и минимальный из них добавить ко времени пребывания установки в пункте ( j ).

Если сначала по времени установка приезжает в пункт ( m + 1), а затем в пункт ( j ), то все рассуждения сохраняются, только пункты в них меняются местами.

В общем случае может получиться так, что две установки будут какое-то время работать в одном пункте одновременно. Если такое невозможно в силу технических особенностей пункта, то придется наложить еще одно ограничение на время прибытия установки в пункт.

Теперь осталось перебрать все пункты, каждый из которых поочередно сделать дополнительным, и решить задачу, выбрав наилучший с точки зрения критерия оптимальности (8) вариант.

Блок-схема алгоритма решения задачи (2)– (11) (Алгоритм 2) представлена на рис. 3.

Вычислительная сложность Алгоритма 2 еще выше, чем Алгоритма 1. Добавление еще одного пункта в алгоритме перебора всех разбиений и всех последовательностей обхода приводит к сокращению количества исходных рассматриваемых пунктов, иначе время работы программы, реализующей алгоритм, становится неприемлемым.

При некоторых значениях исходных данных оптимальное решение задачи (1)–(8) может полностью совпадать с оптимальным решением задачи (2)–(11). В этом случае в оптимальном решении задачи (2)–(11) будет подмножество пунктов, в котором пункт, посещаемый дважды, будет стоять в перестановке на соседних позициях. Это означает, что установка не будет покидать данный пункт, а отработает в нем весь требуемый промежуток времени, а это и есть решение задачи (1)–(8).

ЗАКЛЮЧЕНИЕ

Мы рассмотрели две модели задачи построения графика работы нескольких передвижных установок, обслуживающих территориально удаленные пункты: с единственным посещением каждого пункта (1)–(8) и одним дважды посещаемым пунктом (2)–(11). Эти задачи являются расширениями задачи маршрутизации с временными окнами. Расширение заключается в дополнительном ограничении на выполнение ра- боты в каждом пункте, продолжительность выполнения которой зависит от технических характеристик установок, и учете в целевой функции затрат не только на перемещение установок между пунктами, но и на выполнение работы.

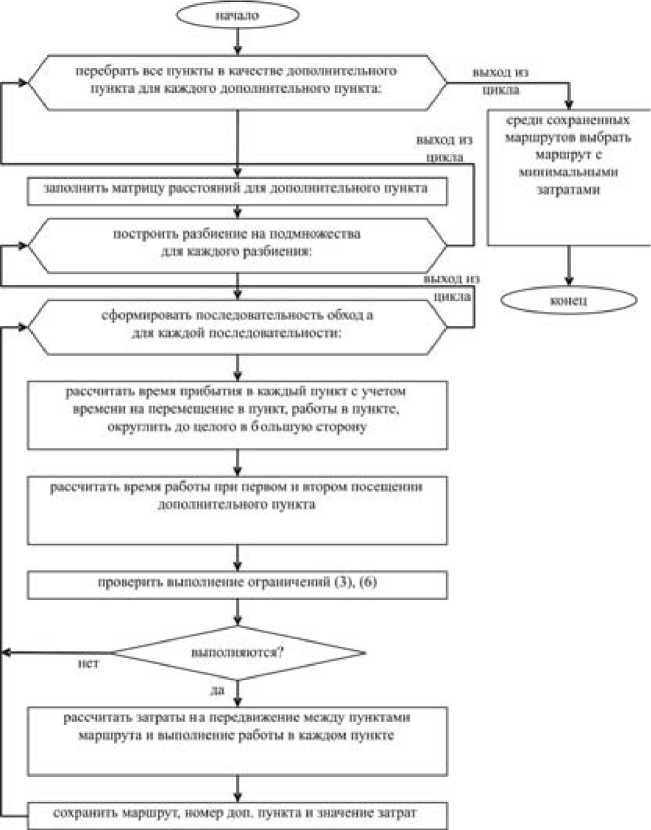
Рис. 3. Блок-схема алгоритма решения задачи с одним дважды посещаемым пунктом (Алгоритм 2)