Задача преследования объекта с поверхности, расположенной над поверхностью преследуемого

Задача преследования как область теории дифференциальных игр возникла как необходимость разработок приложений в военном деле. Первые труды в этой области связаны с работами Р. Айзекса, Л.С. Понтрягина, Н.Н. Красовского, Л.А. Петросяна. Дальнейшее развитие основоположников теории дифференциальных игр привело к развитию приложений на плоскости («катер-торпеда») и в пространстве (самолеты) с различными модификациями задач. Мы в своей работе провели компьютерное моделирование задачи преследования, когда объекты находятся на поверхностях, расположенных одна над другой. Современное состояние IT-технологий позволяет производить моделирование поверхностей для этой задачи, мощность и миниатюризация современных микропроцессоров позволяют в режиме реального времени производить расчет координат дронов и мобильных роботов по разработанным алгоритмам. Современные средства коммуникаций позволяют производить требуемый обмен данными в поставленной задаче. Состояние компьютерной графики позволяет выполнить визуализацию процесса преследования. В этой связи мы считаем, что такая постановка задачи может обладать новизной и актуальностью.

Постановка задачи

В данной статье рассматривается задача преследования, когда преследуемый объект («Кролик») передвигается по поверхности P r ( u , v ) . Преследующий объект движется по поверхности P f ( u , v ) . Пусть R r ( T ) – точка положения «Кролика» на поверхности P r ( u , v ) , в момент времени T , а R f ( T ) - точка положения «Лисы» на поверхности P f ( u , v ) в тот же момент времени. В точках 7— _r ( T ) и R f ( T ) поверхностей P ( u , v ) и P f ( u , v ) , соответственно, построим динамические локальные базисы ^ E 1 E — 2 E — ₃ J и ^ Q — 1 Q — 2 Q — ₃ J (рис.

• —     1 dR _r ( T )    —     1 dR _f ( T )

• 1) . Где E i =       - и Q i =             . Где ^V _r

Vr  dT          Vf   dT и Vf – постоянные по модулю скорости «Кроли- ка»

и «Лисы».

—* n f

—

Q 2

в точках

——

E 3 и Q 3 - единичные нормали n r ,

R_r ( T ) и I* f ( T ) . И E — 2 = E — 3 x E — 1 ,

= Q 3 x Q 1 .

Далее, будем считать, что плоскость Σ обра- зована векторами E1 и E2 , а плоскость П – векторами Q1 и Q2 . Для выбора решения «Кроликом»

нам надо спроецировать точку R _f на плоскость Σ и получить ее проекцию R^' _f для анализа, на предмет из какой четверти плоскости Σ приближается проекция «Лисы». Точно так же для принятия решения «Лисой» необходимо спроецировать точку R_r на плоскость П, получить ее проекцию R^'_r , для того чтобы проанализировать, в какой четверти плоскости П она находится.

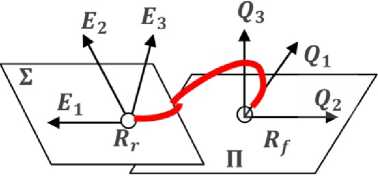
Рис. 1. Динамические базисы

Итак, целью статьи является детальная разработка алгоритма и написание программы в системе компьютерной математики «MathCAD» для указанной выше задачи преследования.

Моделирование поверхностей

Моделирование поверхности P_r ( u , v ) , по которой движется «Кролик», производится заданием точек линий горизонталей в среде «AutoCAD» с последующей полиномиальной регрессией в среде «MathCAD» при помощи встроенных функций математического пакета. На полученной после полиномиальной регрессии поверхности вводится равномерная сетка с расчетом частных производных в узлах сетки.

С моделью поверхности, по которой движется «Лиса», в нашей программе дело обстоит так. К поверхности «Кролика» P_r ( u , v ) строится эквидистантная поверхность (рис. 2) P ( u , v ) = = P_r ( u , v ) + A R • n_r , где A R - расстояние, на которое эквидистантная поверхность отстоит от исходной.

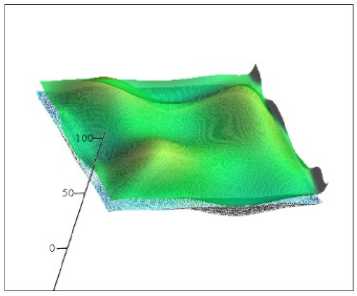
Рис. 2. Эквидистантная поверхность

Потом вводится горизонтальная плоскость z = r ₀ , и поверхность P f ( u , v ) составляется следующим образом:

P f ( u , v ) = <

z , если P e ( u , ^v ) z <  r o ; ?             ?

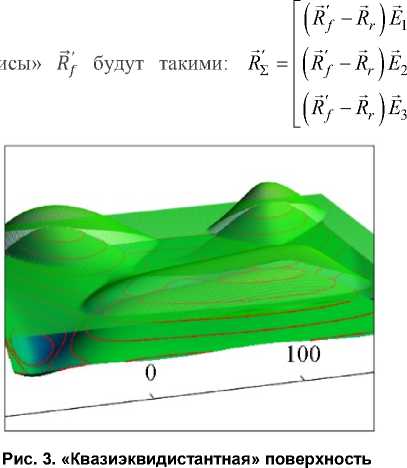
_Pe (u,V),еслИ pe (u,V)z > ro, где r0 – некоторое пороговое значение высоты

(рис. 3). После этого на поверхности Pf (u, v) вво- дится равномерная сетка с расчетом частных производных в узлах. На рис. 3 поверхность Pf (u, v) представлена в полупрозрачном виде, а исходная поверхность «Кролика» представлена с обозначением горизонталей.

Построение проекций в локальных базисах

Если «Кролик», двигаясь по поверхности P (u, v), образует динамический базис |^61 62 63 J, то плоскость S, образованная векторами E1 и E2 , является касательной плоскостью к поверхности Pr (u, v) в точке 6r. Проекция точки Rf на плоскость Σ будет такой:

?    ?    63 ( Т? г — Т? f )

R f = R f +-- —?—- (рис. 4). «Лиса», двигаясь 6 ₃ • 6 ₃

по поверхности Pf (u, v), образует динамический базис |^Q)1 Q)2 Q)3 J . Проекция точки 6r на плос кость Π, образованную векторами Q1 и Q2 , будет

?    ?    6 3 ( R f - R_r )

такой: R'= R_r +--Л?—?—- (рис. 5).

r r       Q 3 • Q 3

Тогда в базисе ^ 6 ? 1 6 ? 2 6 ? ₃ J локальной системы координат «Кролика», координаты проекции

.

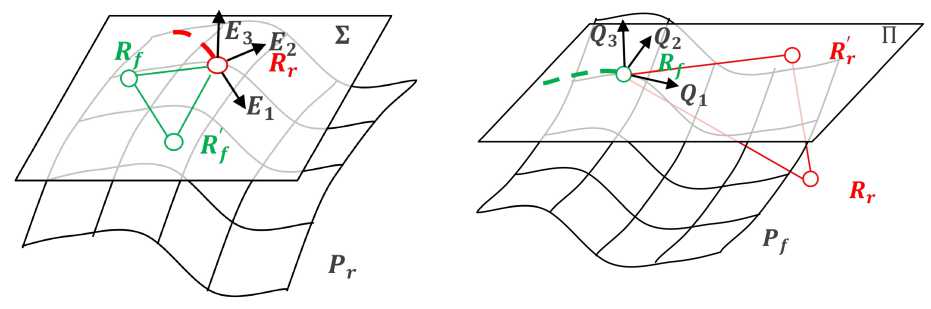
Рис. 5. Проекция «Кролика»

Рис. 4. Проекция «Лисы»

В локальной системе координат [ Q i Q 2 Q 3 ] «Лисы» координаты проекции «Кролика» R_r^' бу-

	[( R;	- R, ) Q
. дут такими: R п =	( R r	- R . ) Q
	( 7 ■	- 7 , ) Q 3 ]

. Необходимо отметить, что

( R , - R, ) E 3 = 0 , ( Rr- мировой системы

- R f ) Q 3 = o .

На плоскости Σ в системе координат «Кролика» «Кролик» имеет нулевые координаты. Анализ координат «Лисы» «Кроликом» состоит в том, что если «Лиса» находится в нижней полуплоскости 2 , то «Кролик» совершает шаг против часовой стрелки (рис. 6). Если «Лиса» находится в верхней полуплоскости, то «Кролик» совершает шаг по часовой. То есть новые координаты «Кролика» за промежуток времени Δ T равны в системе координат плоскости 2 :

Базис

[ H i H 2 H з J в системе координат будет выглядеть так:

координат

«Кролика»

-----►

-----►

H 2 =

-----► где His =

H 1 2 H 2 2 _ H 32 _ >   —	, > >	-----► ----►
H 1 ■ E i	H 2 ■ E 1	H 3 ■ E 1
-----► ----►	-----►                  -----► ----►	--   -- -
H 1 ■ E 2	. H 2 S = H 2 ■ E 2	. H 1 2 = H 3 ■ E 2
-----► ----►	-----► ----►	> >
H 1 ■ E 3	H2 ■ E 3	H 3 ■ E 3

.

? R,‘2=^ Vr ■ AT ■ V- A T ■ I cos (tor - AT) sin (tor - AT) 0

cos ( to _r ■A T ) - sin ( to _r ■A T ) 0

.if (7? f - 7? r ) ■ E ₂ <  0;

,if ( R f - R r ) ■ E ₂ >  0.

Аналогичное можно сказать про выбор направления движения «Лисой». Если «Кролик» находится в верхней полуплоскости П, то «Лиса» совершает шаг против часовой (рис. 7). Если в нижней полуплоскости, то по часовой стрелке:

cos ( to _f - A T )

А в системе координат «Лисы» будет так:

>

		H 1n
H n = --	[	- H 2n [ H 3П ] —- —- H 1 ■ E 1 ----►      -----	, --	[ H 2 ■ E 1 " -----►       -----	--	—”  —- H vE 1
где H 1n =	H 1 ■ E 2		. H 2П =	H 2 ■ E 2	, H 3n =	H 3 ■ E 2
	-[■	----►      ----- H 1 ■ E 3		—”  —- [ H 2 ■ E 3 ]		_ H 3 ■ E 3 ]

.

Of

Rfn

Vf ■A T ■

- sin ( to f ■

■ T ) .if ( r;

cos ( to _f ■A T )

- R f ) ■ Q 2 < 0;

V f ■A T ■ sin ( to f -A T ) ,if ( R r - R f ) ■ Q 2 >  0.

Выбор направления движения

Нами написана программа, которая в расчетном цикле на каждом шаге делает выбор, в каком направлении двигаться «Кролику» и «Лисе». Пусть to _r u to f - угловые скорости «Кролика» и «Лисы». Для примера рассмотрим выбор направления движения «Кроликом».

Расчет координат на следующих этапах итераций

Ранее мы рассматривали, как будет выглядеть базис [Hi H2 Hз ] мировой системы коорди-

нат в

[ E E 2

локальных динамических базисах

E ₃ J и [ Q 1 Q₂ Q 3 ] . Тогда в мировой

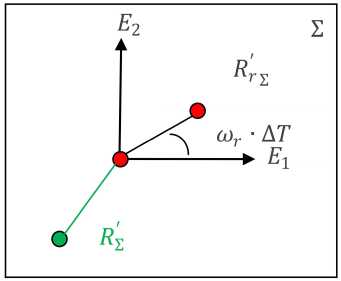
Рис. 6. Выбор направления движения «Кроликом»

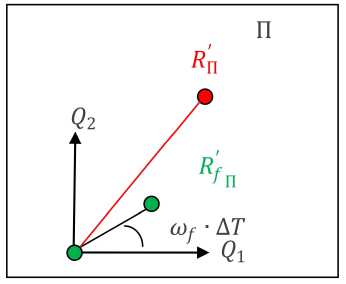
Рис. 7. Выбор направления движения «Лисой»

системе координат |_ H 1 H 2 H 3 J , новые координаты «Кролика» R r _£ на плоскости 2 будут та-

——

R rn

кими:

--—            ——

R r £ = R_r +

^— ‘

R r £

—

R r £

—'

R r £

——

* H 1 £

—

* H 2 £

—

* H 3 £

xrΣ yrΣ

S r ^{( x} r 2 , y r 2 )

——

R fn =

x f П y_{f П}

[ S f ( Х П , Уп ) J

А новые координаты «Лисы» R f П на плоско-

сти П на том же этапе итераций будут выглядеть в мировой системе координат так:

—'     —

R fn * H 1П

Таким образом, мы считаем итерационный процесс в поставленной нами задаче преследования сформированным. Критерием достижения цели в разработанной нами программе служит расстояние между «Кроликом» и «Лисой» в горизонтальной плоскости проекций: ( x r2 ^— -^x Jr²^ ( ^y>2 ^{— y} fVr^ " = R o , где ^R o ^{- неко} "

--►             ——

R f П = R f +

—► '         —►

R fn * H 2П

торое заданное нами пороговое значение.

—— '         ——

R fn * H 3П

Нам нужны вертикальные проекции точек

R r £ , R f n на поверхности P_r ( u , v ) и P f ( u , v ) со

ответственно. Поверхности P_r ( u , v ) и P f ( u , v ) , по которым движутся «Кролик» и «Лиса», всегда

x

можно преобразовать к виду: P_r ( x , y ) =

и P f ( x , y ) =

y

S f ( x , y )

y

S r ( x , У )

. Если координаты точек с

плоскостей Σ и Π представлены в виде

——

R r £ =

x r Σ y r Σ

z r Σ

R /П =

x_{f Π} y f Π

z_{f Π}

соответственно. Тогда

искомые вертикальные проекции точек, как координаты точек на последующих шагах итераций R _rn , R _fn , на поверхностях можно представить в виде:

Результаты

На основе работ [1–4] нами предложена математическая модель задачи преследования, когда участники задачи находятся на разных поверхностях. Приближенно можно считать аналогом преследования с воздуха по траектории, учитывающей рельеф местности. Разработан алгоритм построения траекторий в зависимости от пространственного расположения оппонентов. Предложен метод анализа координат оппонента и принятия решений о выборе направления движения.

В системе компьютерной математики «Math-CAD» разработана программа, реализующая данную модель задачи преследования. С полным текстом программы с подробными комментариями можно ознакомиться на сайте автора [5]. Также там расположен архивный файл. По результатам работы программы изготовлено анимированное изображение, которое вы можете просмотреть на канале автора [6]. На рис. 8 представлен первый кадр процесса преследования. В левой части рисунка поверхность «Лисы» не отображена, видимыми являются только траектории «Лисы», «Кролика» и поверхность «Кролика». В правой части рисунка поверхность «Лисы» отображена в полупрозрачном виде.

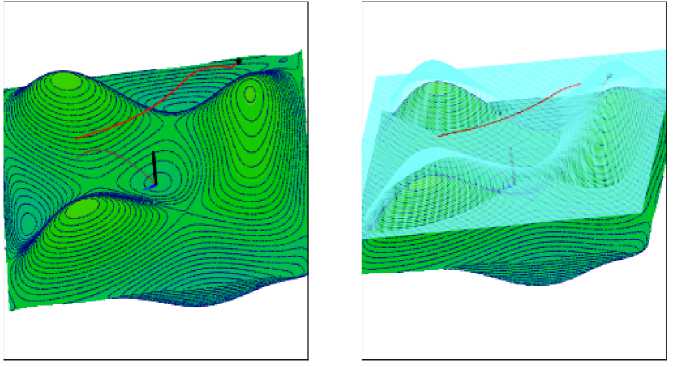
Рис. 8. Преследование по «квазиэквидистанте»

Выводы

В данной статье рассматривалась задача преследования, в которой участники находятся на разных поверхностях. Теоретические аспекты задачи о «водителе-убийце» («катер-торпеда») были рассмотрены в работах Руфуса Айзекса [1]. В работах Л.С. Понтрягина рассматривались теоретические вопросы задачи преследования в пространстве (самолеты) [2]. В работе [3] рассматривалась линеаризованная задача преследования на плоскости с постоянными скоростями и ограниченной кривизной траекторий. В работе [4] рассматривались алгоритмические вопросы управления мобильными роботами в задаче преследования на плоскости. Авторами предложена методика моделирования поведения объектов, участников задачи преследования, в котором присутствуют элементы искусственного интеллекта. Постановка задачи в данной статье предполагает дальнейшее развитие в плане прогнозирования траекторий, получения информации о предполагаемых действиях оппонента в задаче преследования и в плане учета физических характеристик среды, в которой идет преследование.

Мы считаем, что результаты исследования, изложенного в данной статье, могут быть востре бованы разработчиками робототехнических комплексов с элементами искусственного интеллекта.