Задача со смещением для уравнения третьего порядка в частных производных с переменным коэффициентом

Необходимо отметить, что некоторые прикладные задачи приводятся к рассмотрению уравнений третьего порядка с частными производными. В частности, вопросы фильтрации жидкости в пористых средах, передачи тепла в гетерогенной среде, влагопереноса в почвогрунтах приводят к модифицированным уравнениям диффузии, которые являются уравнениями в частных производных гиперболического типа третьего порядка[1]-[7].

В односвязной области   D = {(x, t): |x| < 1 ,0 < t < T} рассматривается уравнение Lu = unx- sgn x • ut = f(x, t).(1)

Задача. Найти регулярное в D \ {x = 0} решение уравнения (1) из класса C(D) n C1 (D) n C2 (D), удовлетворяющее краевым условиям ux (-1, t) = ^u(0, t),   ux (-1, t) = ^u(0, t),   u(1, t) = 0,     0 < t < T(2)

и нелокальным условиям

u(x,0) = avu(x, T) ,    0 < x < 1;(3)

u(x, T) = a2u(x,0),   -1 < x < 0, где ^, ^, av, a2 — const.(4)

Пусть D₊ = D n { x >  0 }     D = D n { x <  0 } .

Пусть решение задачи (1), (2), (3), (4) существует, принимая, что u (0, t ) = t ( t ) , u_x (0, t ) = v (t ) , причем т ( t ) , v ( t ) e C [ 0, T ] и следовательно т (0) = t (T ) = 0 , v (T ) = v (0) = 0 , тогда решение задачи u (0, t ) = т ( t ) , u_x (0, t ) = v ( t ) , u ( 1 , t ) = 0 , u ( x ,0) = ф_й ( x ) , x e [ 0, 1 ]

в области D допускает интегральное представление

tt nu(x, t) = J G^ (x, t; 0, n)r(n)dn - J G^ (x, t; 0, n)v(n)dn +

о

о

+ J G ⁺ ( x , t ; 5 , 0) u ( 5 ,0) d ^ - JJ G ⁺ ( x , t ; £ n ) f (5, n )d& n , 0                               D

где G ( x , t ; 5 , n ) - функция Грина данной задачи и решение задачи

и (0, t ) = т (t ) ,    u ( - 1 , t ) = 0 ,     u_x ( - 1 , t ) = 0 ,    u ( x , T ) = ф_т ( x ) ,            x e [ - 1 ,0 ]

допускает в области D представление mu (x, t) = J G - (x, t; 0, n Mn ) dn + J G - (x, t; 5, T) u (5, T) d^ - t                             -1                                                        (6)

- JJ ^{G - ( x} , t ; ^ , n ) f ⁽ £ n ) d ^ d n -

D -

Известно, что      G ⁺ ( x , t ; 5 , n ) = U ( x , 5 ; t - n ) - W ( x , ,, t - n ) , где   U ( x , 5 ; t - n ) - одно из

фундаментальных решений уравнения u_xx ,- u, = 0 , а W ( x, 5 , t - n ) - регулярное

решение сопряженной по отношению к выше рассмотренной задаче краевой

задачи для уравнения W _n - W ^ = 0 . Тогда

G + ( x , t ;0, n ) = u ^ ( x ,0; t - n ) - W ( x ,0; t - n ) =-- x-^ f

3( t - n )^/3   I

x

1/ 3( t - n )^/3 )

- W_{5 5} ( x ,0; t - n ) ,

t

J G *^ ( x ,0; t - n ) T ( n ) d n

t

=- J

^x f ^x

4/ f          1/

3( t - n )^/3   1 3( t - n )^/3

^{T (} n ) d n ^- J ^W _$ ^{( x ,0}; t ^- n ^{) T (} n ) d n

)            0

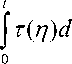
- J w _s ( x ,0; t

+^

J f ⁽ z ) ^dz x

⁽ t - n 0

x

-

tt

- J W. ^ ( x ,0; t - n ) T ( n ) d n = J

x

x

( t - n ) ¹³

J f ⁽ z ) dz

+Ю

T ( n ) d n -

t            ( t -n ) 13                         t                   t

n )?( n ) d n = J r '( n ) J f ( z ) dzd n + J т ( п ) — J W §§ ( x ,0; t - z ) dzd n =

0        +™              0       ^{d n} n

t           ( t -n ) 13                      t             о t

= J r '( n ) J f ( z ) dzd n - J r '( n ) — J W ^ ( x ,0; t - z ) dzd n

0        +™              0       ^{d n} n

Полагая в (6) t = T , с учетом нелокального условия (3) для определения u ( x ,0)

получаем соотношение

TT mu(x,0) = J G + (x, T;0, n)r(n)dn - J G + (x, T;0, n)v(n)dn + 00

llT

+ J G ⁺ ( x , T ; §,0) u( ^ ,0) d ^ - J J G ⁺ ( x , T ; ^ , n ) f ( 5 , n ) d^ n -

00 0

С учетом равенства (7) представление задачи области D можно записать в виде

x

t           ( t -П ) 13                       t

^{T (} n ) J ^{f (} z ) dzd n ^-

0            iv                   0

- J G * (x , t ;0, n ) v ( n ) d n + J G ⁺ ( x , t ; ^ ,0) u ( ^ ,0) d § + f , ( x , t ), 00

n u ( x , t ) = J

J T ( n ) N ( x ,0; t - n ) d n -

t где N(x,0; t - n) = J W^ (x,0; t - z)dz, f, (x, t) = -JJ G + (x, t; ^, n) f (§, n)dd. η

Продифференцируем полученное равенство почленно по переменной x и полагая в нем x = 0, имеем nUx (0, t) = f (0) f т (n) dn - T (n)N x(0,0; t - n)dn —

o(t - n)/3

- Jv'(n)K(0,0; t - n)dn + J Gx (0, ^, t)u(^,0)d^ + fx (0, t) -| nv(t). 0                                0

Продифференцируем равенство (9) почленно по переменной x два раза, полагая в нем x = 0, имеем:

t nUxx (0, t) = f' (0)J

( t - n ) 23

t t ' (n) dn - J t ' (n) N'xx (0,0; t - n) dn +

t

+ f (°)f— 0 ( t - n

tl v' (n) dn - J v' (n) Kx(0,0; t- n) dn +J Gxx(0; ^, t)u (£,0) d^+f. xx(0, t).

В представлении (11) перейдем к пределу при t ^ 0 , и с учетом нелокального условия (4) получим соотношение

T                              0

n u ( x , T ) = J G - ( x ,0,0, n ) T ( n ) d n + J G ^- ( x ,0; ^ , T ) u ( ^ , T ) d ^ -

0                                       - 1

0 T

JJ G ^- ( x ,0; ^ , n ) f ( ^ , n ) d ^ d n .

- 1 0

Для функции u(x, t), определенной выражением (11) можно получить следующие соотношения:

T                              T0

n u x (0, t ) = - f (0) J  ---- -T t '( n ) d n + f L x (0,0; n - 1 ) t' ( n ) d n + f G x (0, t ; ^ , T ) u ( ^ , T ) d ^ +

, (n -1)/з             ,                          Ji

+ f 2 x (0, t ),

TT nuxx(0, t) = -f'(0) f 7----37 T' (n) dn + J Lxx(0,0, n - t )t ' (n) dn +

- (n -1)/з.

+ J G ^- (0, t ; ^ , T ) u ( ^ , T ) d ^ + f _г xx (0, t ),

-l где    L(x,0; n -1) = J W~5 (x,0; z -1)dz,  f z (x, t) = -JJ G- (x, t; ^, n) f (^, n)d^dn.

t                                                    D ^-

В результате получаем, что

TT nv(t) = - f (0) J -----—T T(n)dn + f Lx (0,0, n -tM'(n)dn +

. (n - 1 )^/з               .

+ J G x (0, t ; f , T ) u ( f , T ) d f + f_t x (0, t ),

-l f N /  1 w T(n)dn - jM(n)N (0,0;t - n)dn + f (0) f,  1 v/ v,(n)dn -

• • 0 ( t - n )^/з               о                                       о ( t - n )^/з

• -    f v’(n ) K , (0,0, t - n ) dn + f G + (0, f , t ) u ( ^ ,0) df + f xx (0, t ) = - f ’ (0) T -^-y т’(n ) dn +   ⁽¹⁶⁾

• ^J 0                                ^J0                                                      t ( n - 1 ) ^/з

+ J L xx (0,0; n -1 ) т ' ( n ) dn + J G xx (0, t ; f , T ) u (§, T ) d^ + f _: „ (0, t ). t                                                       - l

К полученным соотношением необходимо добавить следующие уравнения:

n u x ( l , t ) = j G e ( l , t ;0, n ) T ( n ) d n - ] g ; ( l , t ;0, n ) v ( n ) d n + 0 0

+.[Gx+ (l, tf ,0) u (f ,0) df-JJ Gx+(l, t; f, n), f (f, n) dfdn, 0 D+ nux (-1, t) = J G-fx (-1, t; 0, nMn) dn + J Gx - (-1, t; f, T) u (f, T) df -t -l

• -    JJ ^G x ^{- ( - 1} , t ; ^f , n ) ^{f ( f} , n ) ^{d f} d n , D _-

• Таким образом, вопрос существования решения задачи (1), (2), (3) эквивалентно редуцирован к разрешимости системы интегральных уравнений (13), (16), (17), (18).