Задача выбора оптимального закона неоднородного легирования силового стержня для заготовки анизотропного кварцевого волокна типа Панда

волокна. Неоднородное и достаточно высокое легирование стержня приводит к возникновению больших технологических напряжений при изготовлении стержня, которые зачастую приводят к растрескиванию заготовки [5]. Задача выбора оптимального закона легирования ставится с целью подбора необходимых параметров, благодаря которым удастся увеличить общую температурную деформацию силового стержня при выполнении условий прочности на всех технологических этапах производства. При этом известно, что температурная деформация кварцевого стекла увеличивается с ростом концентрации легирующего оксида бора B 2 O 3 . Задача оптимизации решается методом Нелдера-Мида [6] на основе данных, получаемых в процессе решения термомеханической задачи о поведении стержня при остывании от температуры 2100^оС до комнатной температуры с учётом наличия релаксационного перехода из стеклообразного в вязкотекучее (стеклования). Ограничения по условиям прочности учитываются с помощью метода штрафных функций. Параметрами оптимизации являются коэффициенты функции, описывающей закон распределения по радиусу стержня оксида бора в чистом кварце.

Постановка задачи оптимизации. Силовой стержень представляет собой длинный круглый цилиндр радиусом r2=5 10-3 м. Стержень имеет переменную по радиусу степень легирования ц(r) чистого кварца оксидом бора В2О3 на расстоянии от центра до радиуса r1=3 10-3 м, а остальная часть стержня состоит из чистого оксида кварца. При этом содержание легирующих добавок не превышает 10%. В качестве функции, характеризующей величину температурной деформации, используется интегральное относительное содержание оксида бора в элементе стержня единичной длины r1

Ф ⁽ Р i ,...,Р к ) = ^{2 п} J k Р х ,-,Р к ,r ) ^rdr

0 . (1)

Параметрами оптимизации p ₁,^, p k являются коэффициенты функции, описывающей закон распределения оксида бора в чистом кварце.

Задача оптимизации может быть сформулирована следующим образом: найти параметры распределения, обеспечивающие максимальное значение функции (1) (температурную деформацию силового элемента) при ограничениях типа неравенств (условия прочности по первому главному напряжению  о1  и интенсивности напряжений оi):

^{Ф (} Р i ,-, P k ) ^ max, ‘ k ⁽ р 1 ,...,р_к ) < [а р ], _ ^кХР i ,-, Р к М к ]

и ограничениях типа равенств (уравнения краевой задачи по определению остаточных напряжений при изготовлении стержня с законом легирования p( r ); где [ ст р ] - предел прочности на растяжение, [ ст с ] - предел прочности материала на сжатие.

Для преобразования сформулированной задачи с ограничениями типа неравенств и равенств к задаче минимизации без ограничений типа неравенств использован метод штрафных функций [7]. Целевая функция с учетом (1) примет следующий вид:

F ⁽ Р х ,-,Р к ) = ^{- Ф (} P i ,..., Р к ^{) +}

+ А !(к-] - ^mx(Pi,-, Рк))2 •(i - sign к.] - ^Г( p i,-, Рк))))+ + 22 ((кр]- ^Т(рi,-, Рк))2 •(i - sign(кр]- к™(Pi,..., Рк Й)

где ст i ^max и стГ^х - максимальные значения в конструкции интенсивности остаточных напряжений и первого главного остаточного напряжения соответственно, Х_1? Х₂ - весовые коэффициенты для штрафных функции.

Ограничения типа равенств на минимизируемую функцию. Ограничения типа равенств на компоненты тензора остаточных напряжений формулирует математическая модель термомеханических явлений, происходящих при остывании стержня из кварцевого стекла от температур выше температуры стеклования 2100оС до комнатной температуры, которая включает в себя краевую задачу нестационарной теплопроводности и краевую задачу о напряженно-деформированном состоянии (НДС) с учетом неоднородного поля температур и наличия релаксационного перехода (стеклования) в остывающем материале. Постановка краевой задачи нестационарной теплопроводности в области S с границей l содержит:

- уравнение теплопроводности d T

Рс (T)— = div (Х( T )• grad (T))

x е S ,                     ,

где с(Т), Х(Т), р - соответственно теплоемкость, теплопроводность и плотность материала. Диссипативный разогрев полагается пренебрежимо малым из-за низких скоростей деформаций;

- граничные условия

-Х(T)grad(T) • n = а(T)• (T-Тс(t)) + аст0(T)4, x е 13

где первое слагаемое правой части описывает конвективный теплоперенос, а второе - теплообмен излучением по закону Стефана-Больцмана; е - коэффициент черноты, о₀ - постоянная Стефана-Больцмана, а(Т) - коэффициент теплопередачи, Т с ( t ) - температура окружающей среды, n - нормаль к границе l ;

- начальные условия                            Несвязанная краевая задача о НДС с учетом малости деформаций включает:

T (0,x ) = To(x) x е S

,                     .

- уравнения равновесия

div (а) = 0 x е 5

,                     ,

- геометрические соотношения Коши

5=2(vu + (Vu)T) xe5 ,                  , где u(x,t) - вектор перемещений, 5(x, t) - тензор полных деформаций.

- граничные условия в перемещениях и напряжениях

u ( x ) = U ( x ) x e lа ,                 ,

5 • n = P ( x ) x e lа ,                 , где lu, la - части границы с заданными перемещениями и нагрузками соответственно.

Общая система уравнений задачи о напряженно-деформированном состоянии заготовки включает также определяющие соотношения. Механическое поведение кварцевого стекла в широком диапазоне температур (20-2100 ° С) связано с переходом материала из стекло-образного в вязкотекучее состояние. Для описания механического поведения кварцевого стекла с целью адекватного отражения указанных явлений были использованы физические соотношения максвеловского типа:

5= C ••(£ — £ т — 5 в ) , T

ё _т ( x , t ) = E j a ( x , T ( x , t )) dT

T o , ^t

’              U ( x ) ’

n(x, T) = По (x)eRT (x t) , где 4 C - тензор четвертого ранга упругих констант застеклованного материала (изменением упругих свойств при введении малых концентраций легирующих элементов пренебрегаем); ё е (x, t ) = 5(x, t ) —5 T (x, t ) —5 в (x, t) - тензор упругих деформаций, 5(x, t) - тензор полных деформаций; 5 T (x, t) - тензор температурных деформаций; 5 в (x, t) - тензор вязких деформаций; n(x, T), a(x, T) - вязкость и коэффициент температурного расширения материала, зависящие от температуры и от неоднородно распределенных по объему тела легирующих примесей; Т0 -начальная температура, при которой предполагается отсутствие в теле начальных напряжений, деформаций и их производных по времени (гипотеза о естественном ненапряженном и неде-формированном состоянии; 5(x, t) = 5(x, t) —o(x, t)E - девиатор тензора напряжений; a(x, t) = akk / 3 - среднее напряжение; E - единичный тензор второго ранга; R -универсальная газовая постоянная; и(p(x)) -энергия активации. Девиатор тензора вязкой деформации ев(x,t) = 5в(x,t)-^в(x,t)E?, в силу того, что в расплавленном состоянии материал предполагается несжимаемой жидкостью (05 = 0), равен тензору вязких деформаций е?в = 5 в; ^в = вВкк - объемная деформация.

Методика численного решения задачи определения напряженно-деформированного состояния изложена в работе [8].

Решение задачи оптимизации. Для поиска минимума функционала (2) с изложенными ограничениями использован метод Нелдера– Мида. В данной работе зависимость распределения степени легирования от радиуса была аппроксимирована двумя кубическими сплайнами. Таким образом, рассматривались функции распределения легирующего элемента p( r ) вида:

< Ni (r)Ц1 + Ni (r)Ц‘+ NJm (r)Цm + Nm (r)^m,   r e[0,0.00 1 5].Nlm (Г)Цm + Nm (Г)^m + NJn(Г)^n + N (Г)^П, r g[0'00 15,0'003]

где p 1 , p _m , p _n - значения концентрации легирующих элементов в центре стержня, в середине легированной зоны ( r = r 1 /2), в конце легированной зоны ( r = r 1 ) соответственно; Ц] , V _m , Ц _п -значения производных d p/ dr в этих же точках.

В результате имеем шесть независимых параметров оптимизации:

Pl = Ц1  p 2 = ц1 p 3 = Ц m p 4 = ^m

,                              ,                                 ,                                 ,

P 5 =Ц n P 6 =ц П

,.

В качестве ограничений по нормальным растягивающим напряжениям σ1 и по интенсивности напряжений σi использованы следующие значения: [о р ] = 35 МПа, [о с ] = 60 МПа. Последовательные результаты решения задачи оптимизации отражены на рис. 1.

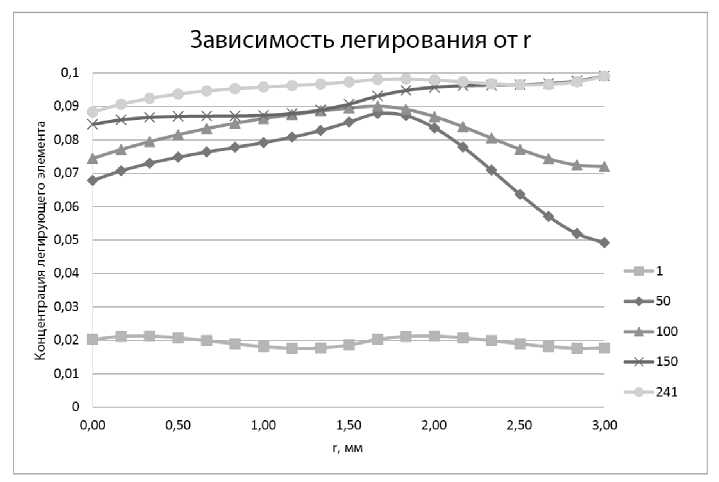
Рис. 1. Изменение зависимости степени легирования силового стержня от радиуса в процессе решения задачи оптимизации, на итерациях № 1, 50, 100, 200 и 241

В результате решения поставленной задачи была определена зависимость степени легирования от радиуса (рис. 1. кривая «241»), позволяющая реализовать в силовом стержне для оптического волокна типа Панда максимальные температурные деформации при соблюдении условий прочности. Результат поиска оптимальных параметров формулы (3) имеет вид:

P 1 =Ц 1 = 0,0869, p 2 =Ц 1 = 0,0299,

P3 =Цm = 0,0977, p4 = ^m = 0,0084, p5 =Цn = 0,1037, p6 =Ц‘п = 0,0413.

Остаточные технологические напряжения в силовом стержне для этой зависимости распределения легирующих элементов приведены на рис. 2.

Выводы: показано, что при изготовлении методом MCVD силовых стержней с переменным содержанием легирующих добавок по радиусу для оптического волокна типа Панда, возможно увеличение величины температурной деформации стержня и, соответственно, улучшение оптических свойств волокна, с помощью использования оптимального закона легирования.

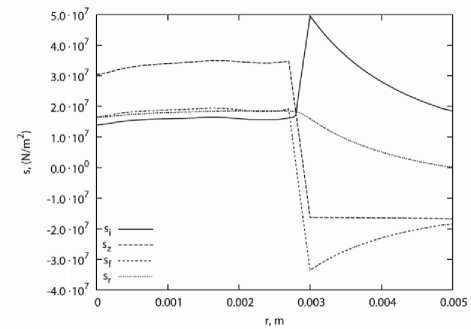
Рис. 2. Зависимость напряжений < т _г (радиальные напряжения), о_ф (окружные напряжения), ^ (осевые напряжения), < r _z (интенсивность напряжений) в силовом стержне для оптического волокна типа Panda от радиуса в случае оптимального легирования

На основе решённой задачи оптимизации можно сделать вывод, что используя полученный закон распределения легирующих добавок можно увеличить величину температурной деформации стержня по сравнению с ранее полученными аналитическими зависимостями, сохранив его прочность. Полученное оптимальное распределение степени легирования от радиуса существенно отличается от используемых на

практике степенных зависимостей вида [8]:

ц ( r ) =

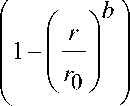
Так, например, параметр, отражающий ^4. величину температурной деформации (1) для распределения вида (4), равен Ф ( р 1 ,…, р k )=9,42 10^-7 при значении степенного аргумента b =4 и 5. a =0,1, а для полученной оптимальной зависимости этот параметр равен Ф ( р 1 ,…, р k )=13,82 10^-7. То есть, при оптимальном легировании удается увеличить общее содержание оксида бора в стержне почти в 1,5 раза при сохранении ^. прочности изделия.                                _7.

Работа выполнена при финансовой поддержке гранта РФФИ проект №13-08-96036 р_урал_а.