Задачи комплектации парка лесовозных автопоездов

В настоящее время особое внимание уделяется проблеме совершенствования лесозаготовительного процесса на стадии транспортировки заготовленных лесоматериалов лесовозными автопоездами. Результаты исследований данного вопроса отражены в научных трудах О. Н. Бурмистровой [2], В. К. Курьянова [6], С. В. Ляхова [8] и др. Колоссальный вклад внесли также ученые и специалисты ПетрГУ: А. В. Кузнецов [5], [10], А. М. Крупко [4], В. М. Лукашевич [7], В. И. Скрыпник [10], Л. В. Щеголева [11] и др. Стоит отметить, что перечисленные работы ученых и специалистов ПетрГУ написаны под руководством профессора И. Р. Шегельмана [10]. Все указанные выше авторы к решению данного вопроса подходили с разных точек зрения. В работе [4] предложена математическая модель рациональной структуры парка лесовозных автопоездов лесозаготовительного предприятия, учитывающая амортизацию автопоездов и сезонный характер лесозаготовок.

При решении названной проблемы целесообразнее учитывать не амортизацию как отдельный экономический показатель, характеризующий объем затрат на содержание лесовозных автопоездов, а показатель затрат на содержание одной машино-смены лесовозного автопоезда, учитывающий амортизационные отчисления, затраты на текущий и средний ремонт, горюче-смазочные материалы и заработную плату рабочих.

В данной статье представлен подход к решению проблемы комплектации парка лесовозных автопоездов, который включает в себя два этапа. На первом этапе необходимо обосновать комплектацию парка лесовозных автопоездов для обновления подвижного состава, используемого на вывозке, на втором этапе – обосновать оптимальную комплектацию автопоездов, используемых на вывозке, учитывая приобретенные и имеющиеся автопоезда.

Для обоснования комплектации парка лесовозных автопоездов с целью обновления имеющегося подвижного состава будем предполагать, что лесозаготовительное предприятие планирует приобрести определенное количество лесовозных автопоездов для выполнения нормированного сменного объема вывозки. Каждый автопоезд характеризуется сменной производительностью и затратами на содержание одной машино-смены. Требуется определить, какое количество автопоездов необходимо приобрести для выполнения сменного объема вывозки.

Для описания математической модели введем обозначения индексов, параметров и переменных, используемых в ней: I – множество индексов марок автопоездов, рассматриваемых для замены подвижного состава; arg min C_i – индекс автопоезда, имеющего минимальные затраты на содержание одной машино-смены; x_i – количество приобретаемых автопоездов марки i ; W – нормированный сменный объем вывозки, м 3 ; P - сменная производительность автопоезда марки i , м³/см; C i - затраты на содержание одной машино-смены автопоезда марки i , руб./м-см; n – количество автопоездов, шт.; C _{arg min C} – минимальные затраты на содержание одной маши-но-смены автопоезда вида arg min C_i , руб./м-см; P _{arg min C} – сменная производительность автопоезда вида arg min C i , м³/см.

Построим математическую модель. Общий объем вывозки заготовленных лесоматериалов ограничен нормированным сменным объемом вывозки:

n

2 P ■ x > W .                 (1)

i = 1

Ограничения на переменные:

x i >  0, x i e Z , i = 1,..., n .                (2)

Целевая функция минимизирует затраты на содержание одной машино-смены всех автопоездов:

n

2 C i ■ x i ^ min.

i = 1

Для решения оптимизационной задачи будем использовать метод динамического программирования [1], [3]. Так как данный метод исполь- зуется для задач с целочисленными исходными данными, а значения Pi и W измеряются в сотых долях, то для нахождения оптимального решения необходимо перевести значения Pi и W в целые числа, умножив на 100.

Пусть функция φ(y) отображает минималь- ные затраты на содержание автопоездов при выполнении объема вывозки y:

n

ф (y ) = min } 2 C i ' x i

n

2 P i 'x i >  У , x i >  0, x i e Z , i = 1,..

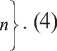
Для хранения номеров автопоездов, при использовании которых достигается минимум функции φ ( y ), введем дополнительный массив ψ ( y ).

Вычислим начальные значения функций φ(y) и V⁽У) при значении У = ⁰ (5), (6) и 0 <  У <  P argmin C (7), (8): - = 1- i

φ(y) = 0(5)

ψ(y) = 0(6)

φ y       arg min Ci,y, ..., arg min Ci i =1..n                                      i=1..n

ψ( y) = argmin Ci.(8)

i = 1.. n

Для определения значений функций φ(y) и v(y) при POrgminC < У < W воспользуемся рекур рентным соотношением Беллмана:

ф⁽ У ) = ““ { ф ⁽ У — ^P ) ⁺ C i } ^, У = P argmi” C .’".’ W , ⁽⁹⁾

i = 1.. n

ψ ( y ) = i .                     (10)

Представленная оптимизационная задача реализована на языке программирования Visual Basic в Microsoft Office Excel [9]. Алгоритм расчета количества автопоездов, необходимых для обновления имеющегося подвижного состава, состоит из четырех этапов.

• 1.    Сортировка по возрастанию исходных данных по критерию «затраты на содержание одной машино-смены».

• 2.    Заполнение массивов φ ( y ) и ψ ( y ) при y = 0 на основе соотношений (5), (6) и 0 <  y <  P - arg min C (7), (8).                                                           - = 1 "

• 3.    Заполнение массивов φ ( y ) и ψ ( y ) при P _argmi n _C <  У <  W на основе соотношений (9), (10).

  - = 1.. n

• 4.    Подсчет количества автопоездов, необходимых для замены подвижного состава, следует начать со значения функции φ ( y ) при y = W , тогда функции ψ ( y ) присваивается значение номера автопоезда ψ ( y ) = i , при котором функция φ ( y ) минимальна. Следовательно, для дальнейших расчетов от нормы сменного объема вывозки вычитаем значение сменной производительности того автопоезда, которому присвоен номер i на предыдущем этапе расчетов, тогда номер следующего автопоезда, включенного в автопарк, равен ψ ( y – P_i ). Подсчет производим до тех пор, пока значение объема вывозки не станет равным нулю ( y = 0).

На втором этапе обоснуем комплектацию парка лесовозных автопоездов, используемых на вывозке. На данном этапе необходимо распределить имеющиеся автопоезда на вывозке таким образом, чтобы выполнялась сменная норма объема вывозки, а затраты на содержание были минимальны. Опишем математическую модель, действующую в задаче. Введем обозначения: J – множество индексов автопоездов, включенных в состав автопарка, используемого на вывозке; n – количество автопоездов, рассматриваемых для комплектации автопарка, используемого на вывозке; x_i – переменная принимает значение 1, если автопоезд j используется на вывозке, 0 – иначе, j ∈ J ; P_j – сменная производительность, выполняемая j -м автопоездом, j е J, м³/см; C j -затраты на содержание одной машино-смены j -го автопоезда, j е J , руб./м-см; R j = 2 P j — сум— j = 1

ма сменных производительностей для k первых автопоездов, м³/см; W - нормированный сменный объем вывозки, м³.

Опишем математическую модель задачи. Общий объем вывозки заготовленных лесоматериалов ограничен нормированным сменным объемом вывозки:

n

2 Pj' xj> w .

j = 1

Ограничения на переменные:

xj e {0,1}, j = 1,...,n.

Целевая функция минимизирует затраты на содержание одной машино-смены всех автопоездов, используемых в технологическом цикле:

2Cj ■ xj ^ min.

j = 1

Как и в первой задаче, для решения будем использовать метод динамического программирования.

Введем функцию φ_j ( y ), которая отображает минимальные затраты на содержание автопарка среди первых j автопоездов при выполнении сменной нормы вывозки y :

. (14)

На начальном этапе расчетов необходимо отсортировать исходные данные по критерию «Производительность в смену» по возрастанию. Объем вывозки для первых рассматриваемых автопоездов j функции φ_j ( y ) выразим через R_j . Объем вывозки для всех рассматриваемых автопоездов функции φ_n ( y ) определяет максимальный объем вывозки, выполняемый всеми рассматриваемыми автопоездами y = R_n . В расчетах необходимо учитывать, что значение сменной нормы вывозки не должно быть больше объема вывозки всех рассматриваемых автопоездов W ≤ R . ⁿ

Для отображения использования рассматриваемого автопоезда при выполнении объема вывозки y введем вспомогательный массив ψ_j ( y ). По значениям массива ψ_j ( y ) будем определять оптимальный набор автопоездов, при котором функция φ_j ( y ) принимает минимальные значения. Если ψ_j ( y ) = 1, рассматриваемый автопоезд при выполнении объема вывозки y используется, если ψ_j ( y ) = 0, автопоезд не используется.

Зададим начальные условия функции φ_j ( y ) и ψ_j ( y ) для первого автопоезда:

ф(y ) = C 1 , если y ^ R 1 ,          ⁽¹⁵⁾

V 1 (y ) = 1, если y ^ R 1 .           (16)

Для нахождения минимальных затрат на содержание одной машино-смены для оставшихся автопоездов построим рекуррентное соотношение Беллмана:

Ф j ⁽ y ) =

min {

j,(max(0,y-Pj)) + Cj,

j_,(y)}, если y<Rj_, Ф_j-1(max(0, y - Pj)) + Cj   если Rj_, < y

, (17)

У = 0,...,Rn, j = 2,...,n,              (18)

где φj–1(y) – функция, отображающая минимальные затраты на содержание автопарка среди предыдущих j автопоездов при выполнении объема вывозки y; max(0, y – Pj) показывает объем работы, которую необходимо выполнить автопо- ездами с индексами j = 1, ..., j – 1; Rj–1(y) – объем вывозки предыдущих j автопоездов.

Определим значения массива ψ_j(y)

1, если ф (y) < Vj-i^y), при y< R^

V j (У) = 10, иначе при y< Rj-1

• 1,    если y > R . .

,                 ^y j-1

Представленная оптимизационная задача реализована на языке программирования Visual Basic в Microsoft Office Excel. Алгоритм расчета состоит из четырех этапов.

• 1.    Сортировка по возрастанию исходных данных по критерию «Производительность в смену».

• 2.    Заполнение массивов φ_j(y) и ψ_j(y) для первого рассматриваемого автопоезда согласно соотношениям (15), (16).

• 3.    Заполнение массивов φ_j(y) и ψ_j(y) для последующих автопоездов согласно соотношениям (17)–(19).

• 4.    Подсчет количества автопоездов, используемых на вывозке, начинается с последнего рассматриваемого автопоезда при значении y = W. Каждый автопоезд можно включить в используемый на вывозке автопарк только один раз, если функция ψ_j(y) = 1, то значение функции для следующего автопоезда ψ_j–1(y – P_j); если функция ψ_j(y) = 0, то ψ_j–1(y). Подсчет автопоездов осуществляется до тех пор, пока значение объема вывозки не станет равным нулю (y = 0).

ВЫВОДЫ

Разработаны математические модели, позволяющие обосновать комплектацию лесовозных автопоездов при обновлении подвижного состава и формировании автопарка, используемого на вывозке на основе минимизации затрат на содержание одной машино-смены.

Принимая в качестве оптимизационного показателя затраты на содержание одной маши-но-смены, лесозаготовитель в одном показателе учитывает амортизационные отчисления, затраты на текущий и средний ремонт, горюче-смазочные материалы и заработную плату основных и дополнительных рабочих.

Используя в качестве ограничения суммарную сменную производительность, рассчитанную в зависимости от технологической схемы, используемой на вывозке, учитывается условие выполнения сменной нормы вывозки.

В настоящее время автором ведется сбор информации для апробации разработанных математических моделей.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

MATHEMATICAL MODELS OF HAULING RIGS' FORMATION