Задачи с параметром, как средство развития исследовательских умений учащихся профильной школы

Развитие творческих мыслительных способностей невозможно вне проблемных ситуаций, поэтому особое значение в обучении имеют нестандартные задачи. К ним относятся и задачи, содержащие параметр. Математическое содержание этих задач не выходит за пределы программы, тем не менее, их решение, как правило, вызывает у учащихся затруднения.

До реформы школьного математического образования в 60-х годах в школьной программе и учебниках были специальные разделы: исследование линейных и квадратных уравнений, исследование систем линейных уравнений. Где ставилась задача исследования уравнений, неравенств и систем в зависимости от каких-либо условий или параметров.

Исследовательская работа – это одно из новых методологических направлений. Она предполагает научное изучение определённой темы. В

России впервые идея исследовательского подхода в обучении была выдвинута просветителем Н.И. Новиковым во второй половине XVIII в.

В школьной практике используется два вида исследовательской деятельности: научно - исследовательская, в результате которой мы получаем новое знание об окружающем мире, и учебно-исследовательская, которая учит универсальному способу получения знаний.

Исследовательская деятельность – деятельность учащихся, связанная с решением творческой исследовательской задачи с заранее неизвестным решением.

Исследовательская деятельность предполагает наличие основных этапов, представленных на схеме.

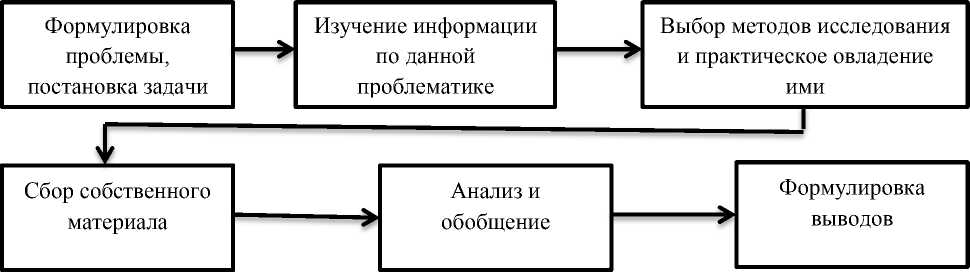
При осуществлении исследовательской деятельности выделяют следующие умения:

• 1)    умение видеть проблемы;

• 2)    умение задавать вопросы;

• 3)    умение вырабатывать гипотезы;

• 4)    умение давать определение понятиям;

• 5)    умение классифицировать, умение наблюдать;

• 6)    умение проводить эксперименты;

• 7)    умение делать выводы и умозаключения;

• 8)    умение структурировать материал;

• 9)    умение доказывать и защищать свои идеи.

Хорошим средством формирования исследовательских умений служат задачи с параметром. Чтобы выделить исследовательские умения, которые используются при решении уравнений и неравенств с параметрами, приведем примеры.

Пример 1: При каких значениях а корни уравнения (а — 2)% 2 — 2а% + а + 3 = 0 положительны?

Решение:

• 1)    Для начала необходимо рассмотреть случай, когда а = 2, так как уравнение принимает вид —4% + 5 = 0. Это обычное линейное уравнение, из которого легко найти корень: % = 5 . Видим, что он положительный, следовательно, нам подходит (умение анализировать параметрическое

уравнение и находить значения параметра, при которых уравнение принимает другой вид).

• 2)    Затем рассматриваем случай, когда а — 2 ^ 0. Если а — 2 ^ 0, то мы имеем право разделить уравнение на выражение а — 2. Получаем квадратное уравнение (умение выполнять равносильные преобразования, учитывая значения параметра):

2а     а + 3

%2 ~%'~ 0

• 3)    Так как у соответствующей параболы ветви направлены вверх, то

данное уравнение имеет два положительных корня в том случае, если эта парабола пересекает ось ОУ в точке, находящейся выше нуля (то есть значение данной функции при % = 0 положительно), абсцисса вершины параболы положительна, а дискриминант квадратного уравнения неотрицателен. Накладывая все условия на данную квадратичную функцию, получаем (умение анализировать график функции в независимости от параметра):

а + 3

---7 >0

а — 2

а

а — 2

> 0

• 6 — а >

1(а — 2)2 “

Получаем решение данной системы: а е (—^; -3) U (2; 6].

• 3)    Объединяем решения, полученные в предыдущих двух пунктах. В

результате получаем окончательный ответ: а е (—^; -3) U [2; 6].

Ответ: а е (—^; -3) U [2; 6].

Пример 2. Найдите все значения а , при каждом из которых уравнение |%² — 2а% + 7| = |6а — %² — 2% — 1| имеет более двух корней.

Решение:

Преобразуем исходное уравнение (умение выполнять равносильные преобразования с параметром):

(%² — 2а% + 7) 2 = (6а — %² — 2% — 1) 2 ^

(%2 — 2а% + 7 — 6а + %2 + 2% + 1)(%2 — 2а% +7 + 6а — %2 —2%

• — 1) = 0

^ (%2 + (1 — а)% + 4 — 3а)(а + 1)(% — 3) = 0.

Последнее уравнение имеет более двух корней или если а = —1, или если уравнение %2 + (1 — а)% + 4 — 3а = 0 имеет два различных корня, отличных от 3 (умение анализировать решение, выраженного через параметр).

( ^{(1 — а)} 2 ^{— 4(4 — 3а)} > 0, ^ (а ² + 10а — 15 > 0,

132 + (1 — а)3+ 4 —3а ^ 0 I 16 — 6а ^ 0.

Откуда а < —5 — 2V10,— 5 + 2V10 < а <  8 или а >  8 .

Исходное уравнение имеет более двух различных корней при а < —5 — 2V10, при а = —1, при — 5 + 2V10 < а < 8 и при а > 8

(умение выражать через параметры корни параметрические уравнения).

Ответ: (—^;

—5 — 2710); -1;(—5 + 2VT0; 8 );( 8 ;+^).

Разобрав решение нескольких примеров, можно выделить следующие исследовательские умения, которые применяются при решении уравнений и неравенств с параметрами.

• 1)    умение определять вид уравнения в зависимости от параметра;

• 2)    умение находить значения параметра, при которых уравнение принимает другой вид;

• 3)    умение анализировать уравнение и подбирать необходимый метод решения;

• 4)    умение выполнять преобразования относительно параметра;

• 5)    умение анализировать график функции в независимости от параметра;

• 6)    умение исследовать графики функций и находить их точки пересечения;

• 7)    умение выражать через параметр неизвестную переменную;

• 8)    умение исследовать функцию на промежутки убывания и возрастания

• 9)    в случае наличия корней (решений) уметь выражать условия наличия того или иного количества корней (решений);

• 10)    умение анализировать решение, выраженное через параметр

• 11)    умение выражать через параметры корни параметрического уравнения.

Сравнивая общие исследовательские умения и исследовательские умения, применяемые при решении параметрических уравнений, можно сделать вывод о том, что серьезным потенциалом в формировании исследовательских умений, таких как умение целенаправленно наблюдать, сравнивать, выдвигать, доказывать или опровергать гипотезу, умение обобщать, обладают уравнения и неравенства с параметрами. Важную роль, конечно же, имеет организация учебного исследования учителем. Обучение приемам мыслительной деятельности, умение осуществлять элементы исследования – эти цели постоянно привлекают внимания учителя, побуждая его находить ответы на многие методические вопросы, связанные с решением рассматриваемой проблемы.