Задачи Соболева для действий конечных групп

Пусть М - n-мерное гладкое компактное многообразие и X - его подмногообразие. Пусть D - эллиптический оператор на многообразии М. Мы будем искать решение сравнения

Du = / mod X, (1)

которое означает, что равенство Du = / выполняется всюду на многообразии М, за исключением точек подмногообразия X. Сравнение (1) не определяет, вообще говоря, фредгольмов оператор. Однако если задать дополнительно некоторый оператор В на подмногообразии X, связанный специальным условием (коэрцитивности) в точках подмногообразия X с оператором D, то пара (D,B) будет уже определять оператор Фредгольма в подходящих функциональных пространствах. Впервые этот эффект заметил С.Л. Соболев (см. [1]). Общая постановка, и исследование этой проблемы принадлежат Б.Ю. Стернину (см. [2]). Впоследствии теория таких задач была, развита, не только для гладких подмногообразий, но также для подмногообразий с особенностями.

В работе строится эллиптическая теория для одного класса, нелокальных задач Соболева, или, более точно, задач Соболева, в которые входят операторы сдвига, отвечающие действию некоторой данной группы на многообразии М.

2.    Постановка нелокальных задач Соболева

Пусть G - конечная группа порядка N и пусть задано бесконечно дифференцируемое левое действие группы G на гладком замкнутом многообразии М, т.е. задан гомоморфизм группы G в группу диффеоморфизмов многообразия М. При этом любой диффеоморфизм g естествеішым образом порождает в пространствах функций. 'заданных на М. оператор Тд'.

Тди(х) = u(g-1x), х G М, называемый оператором сдвига.

Если диффеоморфизмы д^ (г = 0,..., N — 1) задают действие группы G на М, то операторы Тд, задают представление группы G в пространстве функций.

Эллиптическая теория для псевдодифференциальных операторов с конечной группой сдвигов вида

^D = Е ^Dg (^х, ₉х)^Тд,

где Dg - псевдодифференциальный оператор (ПДО) порядка т на М, была построена А.Б. Антоневичем в [3].

Пусть X - подмногообразие коразмерности ? в М.

Определение 1. Задачей Соболева с конечной группой сдвигов на многообразии M будем называть следующую задачу:

j Du = / mod Н^s-m(M, X ), I Ви = һ на X,

где

^D = 5 ^Dg (^ж, ә^⁹,

^В = 5 ^В= ^ ^

- псевдодифференциальные операторы с конечной группой сдвигов на М, Dg - ПДО порядка не выше т, Вд - ПДО порядка не выше Ь, и е нs(m), / е нs-m(M)/нs-m(M,X), һ е нs-b-2 (X), s - Ь - | > о, где Нs-m(M,X) - подпространство пространства Соболева Нs-m(M), которое состоит из функций (распределений), сосредоточенных на подмногообразии X.

Замечание 1. Отметим, что в определении 1 не требуется, чтобы подмногообразие X было G-инвариантным.

Цель работы состоит в том, чтобы дать условия, при которых задача (2) фредгольмова и вычислить её индекс. Решение этих проблем, которое даётся в данной работе, опирается на теорию трансляторов и G-трансляторов. Напомним необходимые сведения из этих теорий.

3.    Трансляторы и G-трансляторы

При изучении задачи Соболева для граничных подмногообразий с особенностями возникает новый класс операторов, которые называются трансляторами. Такие операторы впервые были введены в 1971 г. в работе [4] (см. также [5-8]). Они определяются следующим образом. Пусть граничное подмногообразие представляет собой объединение некоторого числа к гладких подмногообразий Ц|р Ур, р = 1,..., к, пересекающихся трансверсально по гладкому подмногообразию. Транслятор, ассоциированный с парой (M, Ц|р Ур), имеет вид где

Т =

( D 01	Т12	..   Т 1 к
Т 21	0 d 22	..   Т 2 к
.. \ Тк 1	.. Тк 2	.. ..  Dkk
Трч	1 рч	*2 ^pDpq tq*D1

\

/

: ф_р Н ' (У' ) ^ ф_р Н ' (У'),

'3_q : Н^ (У^ч ) ^ Н■ (У^р)

- элементарные трансляторы, Dpч - псевдодифференциальные операторы порядков дрч на соответствующих многообразиях, vp - коразмерность Ур в M, гр : НS(M) ^ Нs-v^2(Ур)

- граничный оператор, индуцированный вложением гр : Ур ^ M, гр* : Н-s+^p/2(Yр) ^ Н-S(M)

• - кограничный оператор, двойственный к гр.

• 4.    Эллиптичность и теорема конечности

Пусть теперь на M действует группа G, как и в параграфе 1, а подмногообразие с особенностями [J _рУ^р является G-инвариантным. Если транслятор Т является G-инвариантным, т.е. он коммутирует с действием группы G, то отвечающий ему G-транслятор Т^G определяется как сужение Т на пространство инвариантных функций относительно действия группы G. Эллиптическая теория для трансляторов была построена в работах [6-8], а для G-трансляторов — в работах [9,10].

Для простоты записи допустим, что G = Z2 = {е,д}, и соответствующие операторы сдвига обозначим через Id, Т. Действие произвольной конечной группы рассматривается аналогично.

Задача (2) может быть переписана в следующем виде (ср. [11]):

I

^(D i + ІЛТ ^)и + г*_х^v = /і г*х (В і +В 2 Т )и = h,

где v - вектор-функция на подмногообразии X, гХ - граничный оператор, индуцированный вложением г : X ^ М, г^х ~ кограничный оператор, отвечающий оператору джета по переменным трансверсальным к подмногообразию X. В локальных координатах этот оператор содержит все производные по трансверсальным переменным до порядка L, который определяется следующим соотношением:

L = 1 ^[т т

—

—

- 8

8 -

—

—

- v/2],     селит v/2 — 1, если т

—

—

—

—

v/2 — не полос число. v/2 — целое число.

Задачу (3) будем обозначать (D,E)

Применяя оператор сдвига Т к каждому уравнению системы (3), получим систему

^(D1 + ^^Т)и + ^х U = /, (ТD1 + ТD 2 Т )и + Тг^х v = Т/, г*_х (В і + В 2 Т )и = к, Тг*_х (В і +В 2 Т )и = ТК.

Лемма 1. Имеют место следующие равенства:

ТгХ = г*хТ, Тг^х = г^Т,

где г*_дх, г*_дх ~ граничный и пограничный операторы, соответствующие влооюению г_дх : gX ^М.

Доказательство. Так как дгх = гдхд, то отсюда следует

• * , *      , * е *     _____/ * гтл — 1 /тч — 1 / *

^гх д = д ^гдх, ^{или г} х^Т =^{Т г}*х •

В

⎛	Di	D 2	-iL г*х	о	⎞	/ и \	1 / \
	ТD2Т	ТD1Т -1	о	i L г*дх		Ти	Т/
⎝	гхВ і	гхВ2	о	о		v	h
	гдхТВ 2 Т	гдхТВтТ -1	о	о		\ Тv)	\ ТҺ)

Обозначим последний оператор через Ф. Этот оператор запишем

в блочном виде:

здесв

^ф Спаус

D       4іау(г^х ,г*дх гх ,г*х )в       о

' I'

Н ^S(M )   \

Н ^S(M )

Н s-m + vJ 2 (x ) \ Н^s-^m + ^/ 2 (gX ) /

^

/ Н ^s-m(M )

Н s-m(M)

Н _s-b-v^/2(X ) \ Н ^s-^b-,^/2(gX J

D = (

D i ТD 2 Т

D2 ТD 1 Т

) ’ в = (

В і

В 2

ТВ 2 Т ТВ 1 Т

)•

В формуле (7) и ниже мы для краткости опускаем числа компонент вектор-функций на подмногообразиях X и дХ .

Оператор Ф будет непрерывным оператором, если выполнены неравенства b + i//2 < s < т — i//2.

Напомним, что для псевдодифференциального оператора А оператор ТАТ = ТАТ ¹ также является псевдодифференциальным, и имеется следующее равенство для символов:

^(ТАТ)(х,О = СТ(А)(д(х),Тд Д, где Тд — матрица, обратная к траиспоииров;пшой матрице Якоби преобразования д. В частности, операторы D и B являются псевдодифференциальными.

Замечание 2. В уравнении (6) матричный оператор Ф действует только на вектор-функции вида

(и,Ти,н,Тн), где и Е Н^s(M ), н Е Н^s -‘ ^v' 2 (\).                     (8)

Пусть на пространстве вектор-функций (Н^s-"^m(M ) ф Н^s"^m(M ) фН ^^b-vl^<2(X ) фН ^s^^u/<2(gX )) определено действие группы G в следующем виде:

MG ТМт Т))- тогда по построению можно проверить, что оператор Ф является G-инвариантным, при этом существует сужение Фс в пространстве G-инвариантных функций вида (8). Отсюда следует

Предложение 1. Задача (3) эквивалентна задаче, отвечающей оператору Ф^й

Далее, используя стандартную процедуру (см., например, [И]), получим следующее

Предложение 2. Если оператор D является эллиптическим, то оператор Ф^с фредгольмов тогда и только тогда, когда фредгольмов следующий оператор:

T^G = diag(i^ ,г*_х )BD 1diag(z^,г^) :

Н_S^-b^-v/ 2 (X ) \^G Н _S^-b-v/2(gX ) j ,

_ (Н^s-m+v/2(X ) \^G / ^: (^Н ^s-m+v/2(gX ) ) Ц

где

( Н s-b-v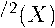 \ ^G

- пространство вектор-функций вида (н, Тн), н Е Н^{s b v/2}(X ).

Н ^S-b-v/2(gX ) )

Выясним тип оператора TG.

Предложение 3. Оператор T^G есть G-транслятор.

Доказательство. Так как операторы B, D являются псевдодифференциальными, то по определению оператор T будет транслятором, ассоциированным с парой многообразий (M,X U дХ ). Теперь надо показать, что он инвариантен относительно действия группы G и действует на пространстве G-инвариантных функций.

Прямой подстановкой мы можем проверить, что коммутатор оператора T и оператора

/ 0 Т\

( Т 0 ) , определяющего действие группы G, равен нулю. Причем из замечания 2 получим, что оператор TG действует только на пространстве функций вида (и, Ти), т.е. на инвариантном относительно действия группы G. Следователь но, оператор TG является G-транслятором.

Определение 2. Задача Соболева с конечной группой сдвигов (3) называется эллиптической, если выполнены следующие условия:

• 2) оператор T^G является эллиптическим G-транслятором в смысле работ [9,10].

5.    Пример

Теорема 1. Если задача Соболева с конечной группой сдвигов эллиптична, то она фредгольмова.

Доказательство. Действительно, если выполняются условия эллиптичности, то для операторов D, T^G существуют почти обратные. Пользуясь стандартным методом решения системы уравнения, мы можем найти и почти обратный для оператора ФД что означает фредгольмовость задачи (3).

Поскольку задача (3) может быть редуцирована к оператору Ф^с и при условии эллиптичности D к G-транслятору T^G, то отсюда получаем формулу индекса.

Следствие 1. (Об индексе задачи Соболева с конечной группой сдвигов.)

ind(D, B) = indDG + indTG.

Отметим, что индекс оператора DG вычислен в [3]. Индекс оператора TG можно вычислить применяя методы работы [6](см. [12]).

Пусть на многообразии М = T⁴ с координатами ж¹, ж², у¹, у² действует группа G = Z2 по правилу

у(ж1,ж2,у1,у2) = (у1, у2, ж1, ж2), а подмногообразия X и gX - его образ при действии группы G - определяются следующим образом:

X = {у¹ = у² = 0}, gX = {ж¹ = ж² = 0}.

Рассмотрим задачу Соболева с группой сдвигов Z2 на М:

J     А²и = / mod Н ^5-4 (М,Х ),

(1 + XT)и = д на X, где А - положительный оператор Лапласа на T4, X - ненулевой вещественный параметр. При этом для простоты рассмотрим интервал 2 < s < 3. Для этого интервала максимальный порядок производной по трансверсальным переменным равен нулю.

Прямое вычисление показывает, что эта задача сводится к G-транслятору:

т ^G = (          ¹

V Хг*_х А^-2г*х (ix А^-2г*х)

Хг*_хА-²г*_дх (г^хА^-2г*дх)^-1 ) _:

/ Н ^5-1(Х) \ ^G / Н ^5-1(Х) \ ^G

^:<Н ^5-1(дХ))  ^ ^Н ^5-1(дХ))  .

(Ю)

Предложение 4. Оператор (гХА^-2г*х)^-1 с точностью до компактного оператора равен оператору Лапласа на подмногообразии X, умножеиному на 4тт.

Доказательство. Пусть В(ж,у,Ә/Әж,Ә/Әу) - псевдодифференциальный оператор на М с символом а(В)(ж, у, ^, д), где £,д - двойственные переменные к ж, у, тогда г*хВг*х ~ псевдодифференциальный оператор на X. Имеет место равенство (см. [5])

о(г*хВг*х )(жД)

о,)-2!

•+^

В(ж, 0, ф p)dp.

^

Применяя этот результат к оператору В = А ², получим

н(Сх А^-2г*х )(€1,€2) = (2,)^-2

+^ +^        1

J-~ -~(^Ғ+ІІ+ДГ+ДІР ^d^^1d^ 2 .

Переходя к полярным координатам, получим

Г 2ТТ    _R тАт               1

'^^Д .*Х Хб.&^РЛ [ .. І0 _(€2 + $ + _г2)2   .  . + ^.

Итак, компоненты транслятора (10) определяются следующим образом:

Т 12 = D^D^D ^ : Н^s—1(gX ) ^ Н ^5—1(X),

Т21 = D^D^D^ : Н5-1 (X) ^ Н8-1 (gX), где символы соответствующих ИДО имеют вид

^D12⁽⁴⁾ = A, ^D22^(4, У) = ₍ 2    2 ¹ 2    2.2 , ^D32⁽^) = ⁴^⁽У2 + у2),

⁽41 ⁺ 42 ^{+ у}1 ^{+ у}2 )

^D21to = X, ^Dh⁽<^,g⁾ =    2    2 2 2 ,  2х₂ , ^D31⁽⁴) = ^4т(41 ⁺ ^

(41 + 42 + у1 + у2 )

Теперь исследуем символ ст(Т) транслятора.

Напомним, что символ ^(T)(z) транслятора (10) вычисляется следующим образом (см. [7]). Заморозим коэффициенты оператора T в начале координат и сделаем преобразование Фурье от переменных ж, у к двойственным переменным 4, У- Получим интегральный оператор Т ‘. Далее переходим в сфери^тюскую систему координат: (41,42) ^ (тцшД. (У1,У2) ^ (^2,^2). Редукция оператора Т ‘ к меллиновской свертке по радиальным переменным с последующим применением преобразования Меллина приводит к оператору умножения на символ:

^(T)(z) = (к ¹( х ^K ^) : ®pL2 (S1) ^ ®pL2(S1).

V K21(z)      1

Здесь компонента K_pq (z) является результатом применения преобразования Меллина по радиальной переменной г к интегральному оператору K_pq (т) с ядром:

Kpq (т,ш,р,ш_ч ) = Dp_q (^p)Dp_q (тш,р,ш_ч )D 3 q (wq ), т = ^Гр.

Tq

В связи с тем, что оператор T является G-инвариантным, его символ ст(Т) сужается на пространство инвариантных функций (u(w1 ),u(w2)). Поэтому мы можем записать действие символа ct( T ^g)(z)(cm. [9]) в следующем виде:

е 7Т

п(ш1) + 4X^y(z)      и(ш₂)Аш₂ = ж(ш1),                          (11)

— 7Т где при 2 < Rez = s < 3

₌ Z⁺” Ат ₌     Z⁺” 2±х_

^Ф(2) V2^ 0   (т² + 1)2 т 2VS о   (т +1)2 ^А

Применяя следующую формулу для Г-функции

Щ= Z“ ДА__ А, Re$ > 0, Rey > 0,

Г(ж + у)   Jq (1 + t)x+y получим явный вид для функции y(z):

y(z) = ^^EUMlzi) =     4z - 1А Г (z - 1) г (2 - z) = v     2V2^    Г(2)       2V2^ 2         2            2

=    1    (2 - 1)^

2V2r sin(2 - 1)^.

Напомним, что G-транслятор (10) эллиптичен, если его символ обратим всюду на прямой Rez = s. Решение уравнения (11) имеет вид

u(w1) = Дсщ) — 4A7ry(z)(1 + 8Атг2

Г yCz))-1

Г(Ш 2 )d,W 2 .

Г

Следовательно, символ ^(T^G)(z) обратим всюду на прямой Rez = s тогда и только тогда, когда функция 9(z) = 1 + 8г²A^(z) не принимает нулевое значение всюду на этой прямой.

Ниже для простоты записи будем использовать обозначения

А' = 2rV2rA.

z' = г 21 — 1) = а + 33

а=г (2—*) ■

Тогда в полосе 0 <  Rez' < Г рассмотрим следующую функцию: 0(z') = sin z' + Az'.

Если 3 = 0. то

9(z3 =0     А' = — —,

а а если 3 = 0, то функцию 6(z') можно переписать в следующем виде:

9(z' ) = sin z' + Az' = sin а ch 3 + А а + (cos а sh 3 + A3 )3

Эта функция обращается в нуль, если её вещественная часть и мнимая часть равны нулю:

{ sin а ch 3 + А а = 0, cos а sh3 + A3 = 0.

Следовательно, tg а th 3 а 3

Однако последнее условие противоречит тому, что

^g-^ > 1 при 0 <а<—, ^6 6 1 при V 3 € (—то, то).(12)

а                 23

Таким образом, мы можем сделать вывод о том, что задача (9) эллиптична, если х       sinr( 2 — 1)

А =--.

2г² v 2г( 2 — 1)

Далее будем предполагать, что задача (9) является эллиптической. Вычислим её индекс. Так как в этом примере D есть оператор Лапласа, который имеет нулевой индекс, то достаточно найти индекс оператора (10).

Через ind_S(T^G) обозначаем индекс G-транслятора (10), действующего в пространстве ^Н^s- 1 (X ) ф Н^s-1(gX )) , он равен числу вращения обратимой функции ^(T^G)(z) (ср. [10]):

ind S(TG) = ws(^(TG))

при изменении z на весовой прямой Rez = s по направлению сверху вниз. Так как ct ( T ^g )(z) имеет вид (11), то число вращения семейства ct ( T ^g )(z) просто равно числу вращения скалярной функции:

y(z) = 1 + A'—                             (13)

sin z на прямой Rez = а = г (^ — 1).

Рассмотрим разбиение полосы значений параметров (А‘,а), 0 < а < - :

А = {Д’ > - —}, В = {-1 < А’ < - —}, С = {А‘ 6 -1}. а                     а

Сначала ищем индекс в области А.

Покажем, что в области А образ прямой Rez = а комплексной плоскости при отображении z ^

не пересекается с отрицательным лучом вещественной оси, то есть число вращения функции ^(z) равно нулю.

В самом деле, заметим, что

Im y(z) =

• 3 sin а ch 3 - а cos а sh 3 | sin(а + г3)І2

  А‘.

  
  

  Следовательно,

  
  

Im^(z) = 0 ^^ 3 "g— = th3. а

Поэтому, сравнивая последнее с (12), делаем вывод, что мнимая часть функции y(z) равна нулю тогда и только тогда, когда 3 = 0.

Далее, подставляя 3 = 0 в (13). получим

Re^(z) = 1 + А’ — sin а

> 0 .

Итак, индекс задачи (9) в области А равен нулю. Теперь вычисляем индекс в области В с помощью относительной теоремы об индексе (см. [7]).

Для каждой точки (А‘,аД области В существуют числа ао,а2 со следующими свойствами:

• 1)    точка (А‘, ао) находится на. границе между областями А и В. т.е. А’ = - ^s™“ 0 (ао соответствует особое значение so = 2(^ + 1), при котором задача (9) не эллиптична),

• 2)    точка (А‘, а2) принадлежит области А т.е. 0 <  а2 < ао < аі < 2.

Рассмотрим разложение Тейлора функции y(z) в окрестности точки ао:

• 1    + А’ z = 1 + - sin ао А ___________ ао + (z - ао) ____________=

sin z            ао   sinаo + (z - аo)cosаo + O((z - ао)²)

= (z - ао) ^{ао cos аo - sin аo} + o((z - ао)2).

ао

Поэтому число полюсов функции y(z)-1 в полосе комплексной плоскости между прямыми Rez = аі 11 Rez = а2 равно 1. А так как а2 < аі- то индекс в области А будет равен inda1 (TG) = inda2(TG) - 1 = 0 - 1 = -1.

Далее из соображений непрерывности следует, что индекс задачи (9) в области С равен индексу в области В.

Итак, доказана следующая теорема.

Теорема 2. Задача (9) эллиптична, если выполняются следующие условия:

sin л( | - 1)

2 < s < 3,  А =--2----’—

.

2 я2 V2^( 2 - 1)

При выполнении этих условий индекс задачи (9)

sin -( 2 — 1)

-

• 1)    рассей 0. если ^А > -7272-1-7 • sin -( 2 — 1)

• 2)    равен, -1, если ^А< ^-2-272-1-7 •

Замечание 3. В предыдущем примере нелокальный оператор присутствует только в граничном условии. Однако этим же методом можно рассмотреть задачи Соболева с конечной группой сдвигов, в которых нелокальный оператор присутствует в основном уравнении. Например, рассмотрим задачу

I

((д2 + э2) - V2d2T)u = / n = д mod НS-2(M,X), на X.

И соответственно задача может быть сведена к G-транслятору:

*   ⁸І _„Ы*   ^ І Л ^ У     -1

^гх 8 4 + 8 4 ^г*9^{х (г}дХ 8 4 + 8 4 ^г*9^х )

1 У               1 у

G

82           . . 82 +82      .   .

• ^гХ 8 4 + 8 4 ^г*9^{х (г}Х Q 4 + 8 4 ^г*^х ) ^{1 у              1 у}

• ( Нs+1(X) )G ^ ( Нs+1(X) у;