ЗАДАЧИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

С физической точки зрения основной задачей, решаемой при управлении технологическими процессами, является получение качественного конечного продукта. Решение этой задачи является многовариантным, зачастую зависящим от состава оборудования на конкретном предприятии, возможностей технологического оборудования и уровня подготовки исполнителей.

Определим, что под качеством конечного продукта понимается его состояние, при котором он полностью удовлетворяет требованиям пользователя этого продукта. Для технических объектов состав эти требований сформулирован в технических условиях (ТУ) на изделие. Отметим, что определение понятия качества не требует от изделия расширения требований более тех, что зафиксированы в ТУ. Тогда при формальном описании задачи управления технологическими процессами состав этих требований позволяет сформировать краевые условия решения.

Дополнительным условием выбора варианта решения этой задачи из допустимого множества является обеспечение надежности технологиче- ского процесса. Согласно стандарту ГОСТ 27.0022009 [1], надежность понимается как "свойство готовности и влияющие на него свойства безотказности и ремонтопригодности, и поддержка технического обслуживания". При этом под готовностью понимается "способность изделия выполнить требуемую функцию при данных условиях в предположении, что необходимые внешние ресурсы обеспечены", а под безотказностью понимается "способность изделия выполнить требуемую функцию в заданном интервале времени при данных условиях".

Однако представленные в стандарте определения ориентированы на изделие как конечный продукт, свойства функций которого не изменяются по времени, по крайней мере до момента, определенного, например, назначенным ресурсом [2, 3]. Особенностью технологического процесса как сложной технической системы является наличие в составе вектора наблюдаемых, но не управляемых параметров системы функции времени [4]. Практика осуществления технологических процессов показывает, что неотъемлемым его атрибутом является деградация по времени, т.е. явление ухудшения параметров и режимов их протекания.

Пожалуй, первое и наиболее полное определение надежности технологического процесса дано А.С. Прониковым [5]: "Надежность технологического процесса — свойство обеспечивать изготовление продукции в заданном объеме, сохраняя во времени установленные требования к ее качеству". Надежность технологического процесса связана со структурой процесса, применяемыми методами контроля и надежностью выполнения отдельных технологических операций.

Ключевым моментом для определения количественных характеристик надежности является понятие отказа технологической операции. Под отказом технологического процесса или технологической операции будем понимать потерю способности обеспечивать качество или объемы изготавливаемой продукции в соответствии с требованиями технической документации. Отказ — это случайное событие, возникающее под влиянием ряда случайных факторов.

ОСНОВНАЯ ЧАСТЬ

Методы

Параметры качества конечного объекта формируют граничные условия при решении задачи управления технологическим процессом, а требования по надежности процесса накладывают дополнительные ограничения на существование граничных условий.

Начальным условием при решении задачи управления технологическими процессами является вектор параметров состояния x ( t ₀ ), определяемый степенью настройки исходных параметров и режимов процесса. Понимание начальных и граничных условий существования позволяет сформулировать обобщенную формальную задачу управления технологическим процессом [6].

С учетом ранее рассмотренного атрибута деградации технологического процесса, определяющего вектор текущего состояния процесса x ( t ), наличия вектора случайных внешних переменных f ( t ), а также при условии обеспечения вектором начальных параметров состояния x ( t ₀) идеальных параметров процесса задача управления может быть сведена к минимизации вектора разности исходного и текущего состояний процесса, т.е. компенсации влияния деградации на качество конечного объекта:

£ ( t ) = { x ( t o ) - x ⁽ t ) } ^ min. (1)

Целью решения этой задачи является нахождение вектора управляющих переменных r(t), обеспечивающих минимум ошибки ε(t), с учетом вли- яния вектора случайных внешних переменных f(t).

При решении этой экстремальной задачи ввиду ее очевидной сложности следует использовать метод последовательных приближений, содержащий:

– этап идеальной, или первичной, оптимизации, состоящий в нахождении идеального, но, как правило, нереализуемого на практике вектора управления r _ид ( t );

– этап вторичной оптимизации, или оптимизации качества управления, состоящий в нахождении оптимального и в то же время реализуемого на практике имеющимися техническими средствами вектора управления r _опт ( t ).

Этап первичной оптимизации заключается в том, что экстремальная задача (1) решается в идеализированной постановке, учитывающей лишь важнейшие свойства системы управления технологическим процессом, основные его параметры и режимы.

Поясним решение задачи первичной оптимизации процесса управления технологическим процессом на примере работы гибкого производственного модуля (ГПМ) механической обработки. В качестве целевой функции примем выполнение производственного задания в минимальный срок [7]. Вектор исходного состояния x ( t ₀) характеризуется идеальной настройкой всех рабочих органов ГПМ и обеспечением всех запасов (заготовок, инструмента, смазочно-охлаждающих жидкостей и т.п.), необходимых для выполнения производственного задания. Вектор управления r _ид ( t ) сформирован на основании общих представлений об алгоритме работы ГПМ и предыдущего производственного опыта, но не учитывает вектор случайных внешних переменных f ( t ), к которым относятся, например, сбои в выполнении кинематических и динамических процессов функционирования рабочих органов ГПМ, а также явления износа обрабатывающего инструмента, ведущие к увеличению погрешностей характеристик конечного продукта технологического процесса [8, 9]. Таким образом, на этапе первичной оптимизации предполагаем вектор внешних возмущений f ( t ) = 0.

Зависимость вектора идеального управления rид (t) от вектора состояния rud (t) = Rид {x(t), t} назовем идеальным алгоритмом управления.

Идеальный алгоритм управления, как отмечалось ранее, можно рассматривать как первое приближение к решению проблемы управления, причем он практически нереализуем. Однако его построение является базовым для дальнейших действий и позволяет упростить нахождение решения, сведя задачу управления к задаче регулирования, т.е. удержания вектора управляющих переменных r(t) в некоторых допустимых пределах относительно вектора rид (t) . Пределы допустимости отклонений вектора r(t) определяются пределами величины деградации параметров и режимов технологического процесса, а также требованиями к состоянию конечного продукта.

Этап вторичной оптимизации заключается в том, чтобы получить решение, наименее отличающееся от идеального и в то же время учитывающее максимально полно ограничения и связи, налагаемые свойствами системы управления, т.е. в том, чтобы получить не только оптимальное, но и реализуемое решение с учетом ненулевого вектора внешних возмущений f ( t ).

При этом следует учесть особенность управления технологическими процессами, которая заключается в том, что в векторе f ( t ) наличествуют в основном два типа переменных, а именно:

• -    Переменные, представляющие собой характеристики случайных событий, не зависящих от времени. Примером таких событий являются сбои в работе рабочих органов технологического оборудования и сбои в выполнении функций вектора r ( t ) .

• -    Переменные, случайные значения которых существенно зависят от времени и образуют временн ы е ряды. Примером таких переменных являются характеристики, связанные, например, с износом обрабатывающего инструмента или старением химических растворов, применяемых в ходе технологического процесса. Общая тенденция изменения этих характеристик по времени, как правило, известна из практического опыта предыдущих реализаций технологического процесса, однако остается существенно случайной в каждый момент действия вектора r ( t ).

В целом решение этих оптимизационных задач в общем виде представляется достаточно сложным в силу многокомпонентности векторов, участвующих в процессе. Однако существует возможность сокращения множественности компонентов, если воспользоваться критерием ошибки (1), т.е. осуществлять управление не по каждому компоненту индивидуально, а по обобщенному компоненту ошибки, который позволит отслеживать в ходе управления не сами величины компонентов вектора состояния x ( t ), а их отклонения от идеального, определенного вектором x _ид ( t ). В такой постановке задача управления технологическим процессом может быть сведена к задаче регулирования процесса.

Условимся называть проблемой регулирования процесса частный случай проблемы управления, к которому последняя сводится при следующих упрощающих предположениях:

• -    идеальный вектор состояния x ид ( t ) предполагается известным, совпадающим с вектором x ( t ₀ ) и отвечающим идеальному алгоритму управления R _ид ( t );

• -    при решении задачи управления решается задача отыскания экстремума обобщенного показателя эффективности управления

с = с {Q, P}, где Q = Q {Е„д - E}, Еид — экстремум цели управления, соответствующий идеальному течению технологического процесса; E — значение показателя цели управления, соответствующее реальному состоянию процесса; P — основная характеристика условия реализуемости управляющей системы, в качестве которой может выступать ее стоимость, сложность как в создании, так и в эксплуатации, степень надежности и т.п. В целом характеристика P может служить обобщенной мерой совокупности всех этих факторов.

Эта задача для целей регулирования распадается на n раздельных или самостоятельных задач отыскания экстремума n показателей эффективности е = Ф{xonm(t)-x(t)} = фi{Si}, i = 1,n, (2)

каждый из которых зависит только от одной составляющей ε_i ( t ) вектора ошибки ε ( t ).

Вектор управления r ( t ) в явной форме зависит не от вектора состояния x ( t ), а от вектора ошибки ε ( t ).

С учетом высказанных предположений проблема регулирования технологического процесса может быть сформулирована следующим образом: предполагая вектор идеального управления r _ид ( t ) известным, найти вектор управления r ( t ) как функцию вектора ошибки ε ( t ), а в общем случае и вектора возмущения f ( t ), который обеспечивает экстремум n частных показателей эффективности (2) и удовлетворяет имеющимся связям, образованным математической моделью управляемой системы и ее ограничениями. В этом случае зависимость можно называть алгоритмом, или законом, регулирования, а вектор r ( t ) — вектором регулирования:

r ( t ) = R { e ( t ), t } . (3)

Таким образом, глобальная задача управления технологическим процессом сводится к задаче регулирования отдельных факторов, определяющих состояние процесса и удовлетворяющих условиям (1).

Однако следует иметь в виду, что эти факторы не являются полностью независимыми друг от друга. Зависимость между факторами обладает рядом особенностей:

• -    Зависимость не должна являться функциональной. В противном случае такие факторы для целей управления процессом должны быть объединены.

• -    Возможно существование корреляционной связи между факторами, что приводит к возникновению случайных связей между составляющими вектора r ( t ) . Факт возникновения такой связи определяется принципиально случайным характером составляющих вектора f ( t ).

Следует отметить, что вектор состояния x ( t ) может содержать не только параметры, но и признаки, которые косвенно отражают качество технологического процесса. В качестве таких признаков могут служить в том числе и параметры изготавливаемых изделий. Для оценки влияния признаков необходимо внедрение в контур управления технологическим процессом дополнительной интеллектуальной системы обработки, которая позволит установить зависимость (4) между признаками и подлежащими контролю параметрами:

• x    пр ( t ) = X { x ( t ), t } . (4)

Для формирования таких систем целесообразно использовать методы машинного обучения и искусственного интеллекта [10, 11], а также эмпирические и имитационные модели процессов [12, 13].

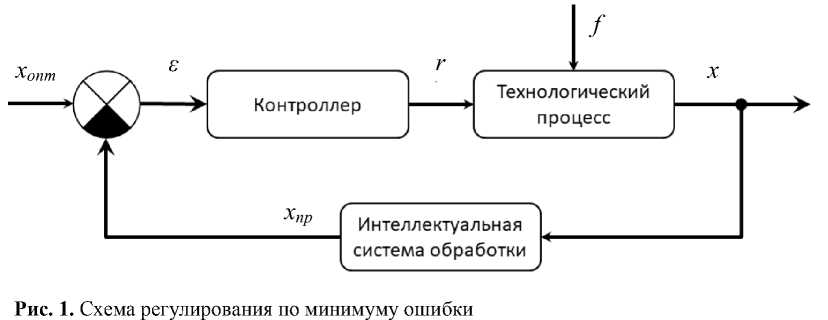
Схема регулирования технологического процесса, учитывающая разделимость минимизации ошибки по каждой составляющей вектора, представлена на рис. 1.

Механизм разделимости ошибки наиболее эффективно работает именно для технологических процессов, в которых целый ряд составляющих вектора f ( t ) оказывает влияние в течение не всего процесса, а только его частей — технологических операций.

Эксперименты, новые закономерности

Рассмотрим высказанные выше положения на примере задачи управления участком цифрового производства для выполнения технологической операции травления печатных плат (ПП). Эта операция, как и большинство химических операций [14], наиболее полно отражает исходные положения об "аналоговости" процессов, производимых при ее осуществлении, и деградации исходного вектора состояния x ( t ₀).

Основным параметром, влияющим на результат технологической операции, является время травления, которое в данном случае определяет вектор регулирования r ( t ). Однако в настоящее время отсутствуют строгие аналитические зависимости, связывающие время выполнения операции и состояние травильного раствора, особенно с учетом его постоянной и зачастую случайной деградации. На основе анализа операции [15] выделены основные параметры, влияющие на время травления и время использования подготовленного травильного раствора с исходным состоянием x ( t ₀) (рис. 2).

Всего можно выделить три категории параметров:

• 1)    параметры травильного раствора, которые в большей степени определяются его составом и объемом;

• 2)    технологические параметры, такие как: расположение заготовки в ванне травления, температура раствора, температура окружающей среды,

  

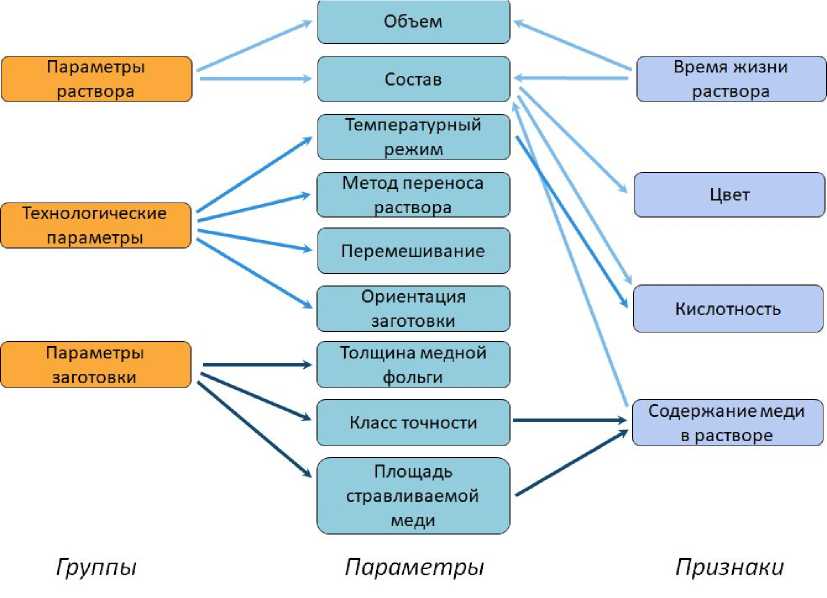
  Рис. 2. Параметры, определяющие время травления заготовки и время использования подготовленного травильного раствора

  
  

способ переноса раствора на заготовку, перемешивание раствора;

• 3)    параметры заготовки, а именно: количество стравливаемой меди, т.е. толщина слоев медной фольги, площадь стравливаемой меди и класс точности изготавливаемой ПП.

Оценить прямое влияние некоторых параметров, например времени перемешивания, на качество процесса затруднительно, или же оценка потребует большого количества трудоемких ручных операций, что относится к исследованию состава раствора. Поэтому вектор состояния x ( t ) для управления технологической операцией травления содержит в себе как параметры, напрямую влияющие на качество процесса, так и признаки, которые косвенно отражают качество операции.

В качестве контролируемых параметров выбраны:

• -    температура раствора;

• -    объем раствора;

• -    толщина медной фольги на заготовке;

• -    площадь стравливаемой меди;

• -    класс точности изготавливаемой ПП.

Также в контролируемый вектор состояния x ( t ) включены следующие признаки:

• -    время жизни раствора, т.е. время, прошедшее с момента приготовления раствора до текущего момента времени;

• -    цвет травильного раствора;

• -    кислотность травильного раствора;

• -    содержание стравленной меди в растворе.

Стоит отметить, что такие параметры, как режим перемешивания, ориентация заготовки и метод переноса раствора, не включены в вектор состояния x ( t ), т.к. они в большей степени обусловлены конструкцией установки травления и не имеют возможности изменения. В частности, эксперименты проводились на лабораторной установке погружного травления с вертикальным расположением заготовки без перемешивания, а в качестве травителя использован раствор, который состоит из 1.5 л дистиллированной воды, 150 мл персульфата аммония, 35 мл поваренной соли.

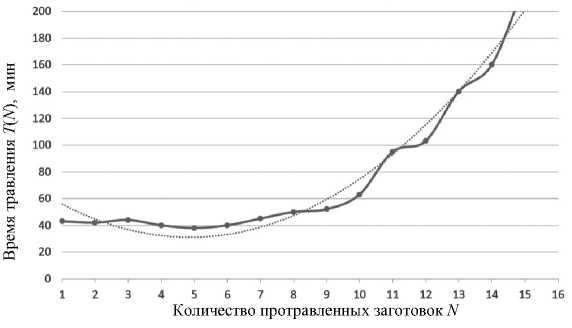
Рис. 3. Зависимость времени травления T заготовки от количества N протравленных заготовок.

Сплошной линией показаны результаты эксперимента; пунктирной — эмпирическая зависимость T ( N ) = 1.65 N ² – 16.08 N + 70.33

Проведенные эксперименты с последовательным травлением 15 однотипных заготовок двустороннего фольгированного стеклотекстолита FR4 с размерами 80 × 80 мм с толщиной меди 35 мкм позволили построить зависимость времени T травления заготовки от общего количества N протравленных заготовок, по которой можно оценить степень деградации травильного раствора (рис. 3).

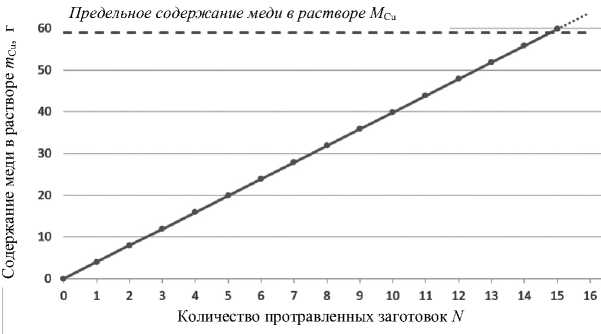
Рис. 4. Зависимость содержания меди M Cu в растворе от количества N протравленных заготовок

С помощью метода наименьших квадратов, ограничившись уравнением второго порядка, получена эмпирическая зависимость (5) с коэффициентом детерминации 0.97:

T ( N ) = 1.65 N ² - 16.08 N + 70.33.        (5)

Зная емкость по меди раствора [16], определим предельное содержание меди M Cu [г] в растворе по формуле (6):

M cu ( V s ) = JV_S = 58.98,               (6)

где: j — емкость по меди раствора, 35 г/л; V _S — объем раствора, 1.88 л.

Поскольку в ходе эксперимента со всех заготовок, кроме последней, произошло полное удаление меди, то количество меди в растворе m _Cu [ г ] в зависимости от количества протравленных заготовок N можно вычислить по формуле (7):

m Cu ( N ) = 2 ShpN x 10 ^{- 9} = 4 N , (7)

где: S — площадь стравливаемой поверхности платы, 6400 мм2; h — толщина медной фольги, 35 мкм; ρ — плотность меди, 8930 кг/м3. Сопоставив значение предельного содержания меди в растворе MCu с полученной зависимостью (рис. 4), можно сделать вывод о том, что в процессе травления 15-й заготовки произошло насыщение раствора медью, что привело к остановке процесса травления.

Сопоставив выражения (5), (6) и (7), получим зависимость времени травления от содержания меди в растворе (8):

T(mCu ) = 0.1 mCu - 4.02mCu + 70.33, mCu ^ MCu ( VS ) .

Дополнительно эксперименты показали, что:

• -    цвет травильного раствора изменяется в значительной мере на начальных стадиях использования подготовленного травильного раствора;

• -    кислотность травильного раствора снижается в ходе выполнения технологической операции с зависимостью (9), которая имеет коэффициент детерминации 0.92:

p H ( t ) = 3.33 х exp { - 4.79 х 10 ^{- 5} х t } , (9) где p H — водородный показатель раствора; t — время жизни раствора, мин.

ВЫВОДЫ

В целом решение задач управления ходом технологического процесса требует предварительных экспериментальных исследований, связанных с формированием вектора исходного состояния процесса x ( t ₀) и определением как вектора управления r ( t ), так и значимости влияния отдельных его составляющих на величину ошибки уклонения состояния процесса от идеального.

Формализация задач управления технологическими процессами позволяет унифицировать как ход формирования набора исходных параметров, так и определение структуры алгоритмов управления и регулирования, что позволит организовать переход предприятий от превентивной к предиктивной модели обслуживания, тем самым снизив вероятность отказа оборудования.

В ходе экспериментального исследования для разработанного опытного образца цифрового участка травления определены составляющие вектора состояния x(t), который содержит как параметры технологического процесса, так и косвенные признаки качества операции. Для учета информации от признаков в контуре управления технологическим процессом получены эмпирические зависимости, связывающие время травления заготовки с содержанием меди в растворе (8), а также время жизни раствора с водородным показателем (9).

Работа выполнена в рамках гранта Президента Российской Федерации для государственной поддержки молодых российских ученых – кандидатов наук (МК-582.2022.4).