Задержка пробоя микроплазмы в p-n-переходе при эмиссии носителей заряда с двухуровнего центра

Многозарядная ловушка может последовательно испускать несколько электронов либо дырок. Особенности тепловой ионизации глубоких центров возникают в случае, когда два близко расположенных уровня принадлежат двум различным зарядовым состояниям одного и того же центра. Эти особенности возникают из-за того, что концентрация центров в определенных зарядовых состояниях перераспределяется между двумя состояниями в процессе ионизации. Конкретный центр может быть в одном зарядовом состоянии. Электроны и дырки эмитируют с центра последовательно, поэтому могут возникать ситуации, когда эмиссия с одного зарядового состояния ограничивает выброс с другого [2].

Если глубокий центр создает два энергетических уровня в запрещенной зоне, то он может находиться в трех зарядовых состояниях. Изменение числа центров в данном зарядовом состоянии возможно в результате: захвата электрона либо дырки на центр, эмиссии электрона или дырки с центра. Для центра, оказавшегося в области пространственного заряда (ОПЗ), первые два процесса исключаются. Существенную роль играет один из процессов эмиссии, вследствие которого центр последовательно переходит из первого состояния во второе, а затем в третье. При этом поступательно уменьшается число носителей заряда на центре. Схема таких переходов показана на рисунке 1.

Рис. 1. Схема термических переходов и зависимость скорости эмиссии с двухуровневого центра от температуры. 1 – е n1 ; 2 – e n2

Рассмотрим для определенности полупроводник n-типа. В качестве начальных условий выберем полное заполнение центров носителями заряда (N20=Nt). Все центры захватили по два электрона. При некоторой температуре, достаточной для перехода электронов с уровней в зону проводимости, концентрация центров в различных зарядовых состояниях будет изменяться. Выброс электрона с уровня, соответствующего состоянию N2, в зону проводимости переводит центр в состояние N1. Вероятность этого выброса определяется скоростью термической эмиссии en2. Только после этого возможен выброс электрона из состояния N1 в зону проводимости, вероятность которого en1. Следовательно, изменение концентрации центров в состоянии N2 происходит за счет одного процесса, а в N1 – за счет двух процессов, что описывается системой кинетических уравнений dNdN

= - en 2 N 2 ;   , = — en i N1 + en 2 N 2

dtdt с начальными условиями N2(0)=Nt, N1(0)=0. При этом в процессе перезарядки центра выполняется условие N2(t)+N1(t)+N0(t)=Nt. Решение системы уравнений (1) дает:

N1 (t) = en'Nt (exp(-en 1 t) - exp(-en2t)) , en 2 - en 1

N2(t) = Nt exp(- en2t) .

Скорости эмиссии электронов из зарядовых состояний N 2 и N 1 будут определяться как

G 1 ( t ) = en 1 N^t ),     G ₂( t ) = en ₂ N ₂( t ) .

Для функции распределения задержки пробоя МП по длительности, обусловленной реэмиссией носителей с двухуровневой ловушки, получено следующее выражение [3]:

1 -

p

Mt

= exp] A

e ~                 e - 2 — 2 e 1      /\ n2                             n2

exP ^(— e n , t ) +             exp e n 2 1 ^{) — 2} f ,

. en 2    en 1                      en 2    en 1

Ln где A = SMNt j Pn (x)dx, Lm, Ln – границы области релаксации носителей заряда с глубоких Lm уровней, SM – площадь микроплазмы; Pn(x) – вероятность запуска лавины носителем заряда.

Для анализа выражение (4) удобно представить в полулогарифмической системе координат в виде

^( t) = Ц1 — PMt ) = ^1 (t) + ^2 (t),

где

^1( t) = A

n 2

e ~ — e .

n 2       n 1

exp(— en 1 t)- 1

^2(t) = A

' n 2    ² e n 1      /       Л 1

----------exP(— en 2 t )- 1

e n 2 ^— e n 1

Физический смысл параметра A состоит в следующем. Величина exp(– A ) есть вероятность того, что по истечении времени, когда установится стационарное состояние ловушки, после подачи прямоугольного импульса перенапряжения, микроплазма не включится. Теоретически это время равно бесконечности.

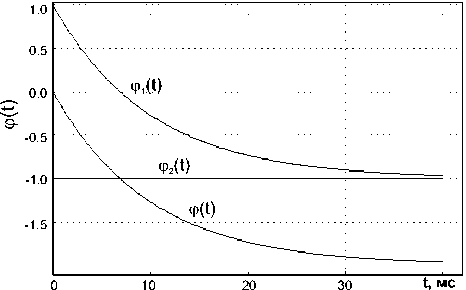
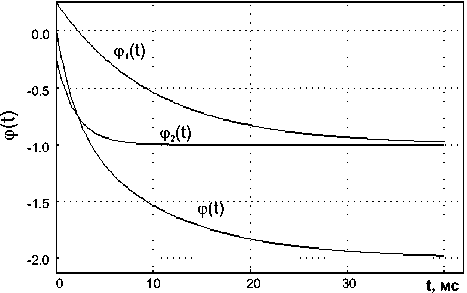
На рисунке 2 приведены результаты расчетов функции ^ ( t ) , ^( t ) и ^ ₂ ( t ) при различных соотношениях e n1 и e n2 . Для удобства расчетов величина A взята равной 1. В определенном диапазоне температур, когда e n1 и e n2 равны или близки друг другу, разделить два процесса перезарядки двухуровнего центра из функции распределения статистической задержки пробоя не представляется возможным (см. рис. 2а, 2б), тем более, если экспериментальная кривая ^ ( t ) не достигает насыщения - величины 2 A . Будет обнаружен только один уровень, но с неверным значением концентрации.

а)

б)

в)

г)

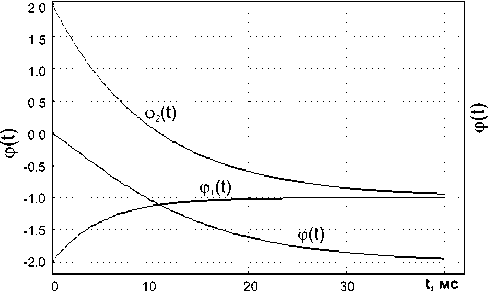
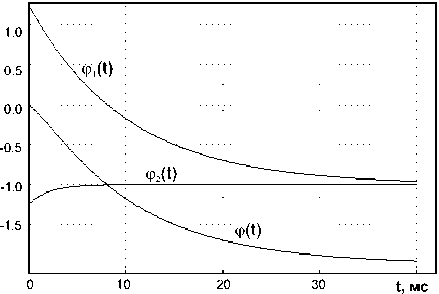
Рис. 2. Функции распределения задержки пробоя микроплазмы при эмиссии e электронов с двухуровневой ловушки.  n1 : а) – 0,5; б) – 2; в) – 5; г) – 0,2.

n 2

Чтобы раздельно определить вероятности ионизации обоих зарядовых состояний, необходимо экспериментально осуществить различные начальные заполнения этих состояний. Если скорости эмиссии с уровней сильно различаются, во всяком случае, более чем в несколько раз, то разделить эти два процесса можно путем аппроксимации кривой ^ ( t ) суммой экспонент и констант. В случае e ni >> e n2 , выброс электронов с зарядового состояния N 2 сильно лимитирует процесс эмиссии с зарядового состояния N 1 , и функция распределения задержки пробоя <р( t ) имеет характерный выпуклый начальный участок (см. рис. 2в). Когда e n1 превышает e n2 более, чем в десятки раз, ϕ ≈ A , и перезарядка ловушки практически определяется скоростью эмиссии носителей e n2 из зарядового состояния N 2 , но с удвоенной концентрацией центров, т.е. с уровня, соответствующего зарядовому состоянию N 1 электроны эмитируют почти мгновенно вслед за электронами из состояния N 2 . При e n2 >> e ni , функция распределения ^ ( t ) имеет такой же вид (см. рис. 2г), что и в случае эмиссии основных носителей с уровней, принадлежащих двум различным по природе центрам [1; 4]. Разделить эти два уровня большого труда не представляет, а идентифицировать уровни можно лишь по концентрации центров.

В результате проведенной работы получено математическое выражение и проведены расчеты вероятности включения микроплазмы в случае эмиссии носителей заряда с двухуровневой ловушки. Показаны характерные особенности в распределении статистической задержки пробоя микроплазмы по длительности, когда два близко расположенных уровня принадлежат двум различным зарядовым состояниям одного и того же центра.