Закон распределения длины максимальной серии и его статистические приложения

Самарский государственный аэрокосмический университет

В статье обсуждается целесообразность использования длины максимальной серии в качестве статистики критерия случайности. Установлены и экспериментально подтверждены законы распределения указанной статистики для двух основных типов серий в случайной последовательности количественных данных. Получены таблицы доверительных интервалов и методики интервальной оценки длины максимальной серии, предназначенные для статистического анализа в прикладных исследованиях.

При статистическом анализе массовых случайных явлений самой различной природы одной из актуальных и первоочередных проблем является оценка того, на сколько обоснованно может считаться случайной последовательность результатов наблюдений (либо отклонений от априорной функциональной зависимости). Под случайностью чаще всего понимается стационарность “в узком смысле” исследуемого процесса, то есть что полученная последовательность представляет собой независимые в совокупности реализации случайной величины (СВ) с неизменным законом распределения. На практике, опять таки чаще всего, исходят из того, что условия случайности соответствуют действительности. Вопросу оценки правдоподобия этого исходного положения, то есть гипотезы случайности посвящен достаточно основательно разработанный раздел математической статистики, объединяемый понятием критерии случайности [1,2]. В качестве статистики критериев случайности используются целочисленные СВ: длина серий, число серий, число инверсий и число циклов случайной последовательности. Наиболее полно исследованы законы распределения двух последних из перечисленных статистик. В частности, установлена их достаточно быстрая нормализация (при длине последовательности n > 20). Несомненным достоинством этих статистик является их универсальность по отношению к закону распре- деления исходной непрерывной СВ, то есть рассматриваются не сами выборочные значения, а их порядковые номера в вариационном ряду. Вместе с тем, как и все статистики кумулятивно-суммирующего типа, они позволяют лишь усреднено оценить характер всей последовательности в целом и могут быть недостаточно чувствительны к ее локальному упорядочению. Для выявления локальных отклонений, как известно, более пригодны критерии, построенные на статистиках селективно-порядкового типа.

Длина максимальной серии, хотя и не в полной мере, все же позволяет отследить оба указанных типа отклонения от случайности. А именно, наличие одной или более аномально длинных серий может свидетельствовать об искусственной группировке по месту их расположения в последовательности. Слишком короткие серии, в свою очередь, указывают на искусственное перемешивание всей последовательности в целом.

Относительно закономерностей формирования серий можно сказать следующее. В [3] было показано, что в последовательной выборке непрерывной СВ существуют два принципиально различающихся типа серий. По предложенной там же классификации “знаковые” – группа последовательных точек, расположенных по одну сторону от центральной линии (медианы) и “трендовые” – группа точек, образующих монотонную последовательность.

Серии первого типа сводятся к последовательным испытаниям по схеме Бернулли и подробно изучены в теории рекуррентных случайных событий [2]. Однако основное внимание в исследованиях было уделено законам распределения числа серий и времени возвращения серии фиксированной длины. Для вероятностей длинных серий в литературе можно найти лишь асимптотические Пуассоновские оценки [1, 2].

Задача же об установлении закона распределения длины максимальной серии, несмотря на свою очевидную “хрестоматий-ность”, осталась несколько в стороне от “магистрального” направления развития теории. Более того, информация о сериях второго типа по существу ограничена лишь указанием о неприменимости в данном случае схемы Бернулли, хотя такие серии представляют ни чуть не меньший интерес. Такое положение выглядит довольно странным, тем более, что задача допускает точное решение вполне элементарными методами.

Рассмотрим закономерности формирования знаковых серий. Как известно, последовательность n испытаний по схеме Бернулли порождает пространство элементарных событий, содержащее 2 ⁿ различимых равновероятных комбинаций.

Введем в рассмотрение целочисленные С. В.: L_n – длину максимальной серии успехов (либо неудач) в последовательности испытаний длиной n и T_l – длину последовательности, оканчивающейся первой серией длинной l . Следуя [2], рассмотрим следующие последовательности вероятностей, связанных с L_n и T_l :

вероятность “первого вхождения” серии длиной l на n ^ом шаге

f (¹ ) = P { L n = 1 ; L n - 1 = 1 - 1} = P { T , = n } , 1 >  2, n >  Серии одновременно. Элементарный способ

вероятность отсутствия серии длинной l в последовательности длинной n

« qn1) = P{Ln < 1} = p{T1> n }= X f(”

k = n + 1

В терминах теории рекуррентных собы- тий fn(l) является рядом распределения времени возвращения Tl , а вероятности qn(l) принято называть хвостами распределения времени возвращения.

Ряд распределения L_n связан с хвостами распределения T_l очевидным соотношением:

p { L n = i } = v n¹ ) = q n^{1 + 1)} - q n¹ ) .     (1)

Как показано в теории рекуррентных событий [2], для вероятностей q_n ^{( l )} серии успехов длинной l справедливо следующее рекуррентное соотношение:

i-i q1) = (1 - p )X pq-k-1 ^                  k=0

_ qn1) = 1, n = 0,1 1, где p – вероятность успеха в одном испытании.

Соотношение (2) получается путем разложения события, соответствующего

вероятности q_n ^{( l )} на полную группу несовместных событий по допустимым значениям длины “финишной” серии успехов: L n = {0,1,..., I - 1}.

В качестве иллюстрации рассмотрим вероятности появления трех шестерок подряд при бросании симметричной игральной кости (табл. 1).

^p = 6, 1 = 3; q о = q 1 = q 2 = ¹;

q n = т⁽ q n - 1 ⁺ ^q n - 1 ⁺ ^q n - 2 ) 6       6      36

Там же в [2], в разделе “более общие рекуррентные события”, рассматриваются события заключающиеся в том, что последовательность содержит либо серию успехов длиной 1, либо серию неудач длиной 0, либо обе непосредственного вычисления вероятностей qn таких событий заключается в следующем. Разобьем полную группу событий, соответствующих qn(l) , на две полугруппы: {… последовательность оканчивается неудачей}, {… последовательность оканчивается успехом}.

Таблица 1. Ряд распределения f_n и хвосты q_n времени возвращения серии успехов T ₃

n qn fn 1 1 0 2 1 0 3 0.995 0.005 4 0.992 0.003 5 0.988 0.004 6 0.984 0.004 7 0.980 0.004 8 0.976 0.004 9 0.972 0.004 10 0.968 0.004 q 1,0    q0,0    1, q1,n    q0,n 0, n < 0

Тогда вероятность q_n можно представить в

( l )          ( l )

виде суммы: q n = q 0 n + q 1, 1/ , а для слагаемых будет справедлива система двух рекуррентных соотношений:

<

l 1 - 1

С = ъ p k q 0 ln - k , n ^ 1

k = 1

^l 0 ^{- 1}

q 0 n ) = Z (1 — P ) k q n - k , n ^ 1, k = 1

( l ₁ )          ( l ₀ )                                              ( l ₁ )          ( l ₀ )

4 1,n ^q 0, n ^o, n <  ^o;         4 1,0 ^q 0,0     ¹-

При условиях предыдущего примера и длине серии неудач l ₀ = 5 получим результат, представленный в табл. 2.

p = 6 , l 1 = 3 , ^l 0 = ⁵

q1,n q0,n

6 ⁽ q 0, n - 1 ⁺ 6 q 0, n - 2 )

= 6⁽ q 1, n - 1 + 6⁽ q 1, n - 2 + 6⁽ q 1, n - 3 + ^ q 1, n - 4 ⁾⁾⁾

Аналогичным образом можно получить рекуррентные формулы для вероятностей q_n любой конечной комбинации успехов и неудач. В частности, например такой, как “два из трех последовательных значений выборки из нормальной совокупности лежат вне центральной 4 σ -ой полосы” и т.д.

В случае, наиболее интересном с практической точки зрения, при р = ¹ , 1 ₁ = 1 ₀ = l

Таблица 2. Ряд распределения f_n и хвосты q_n времени возвращения, комбинированной серии успехов/неудач T _3,5

n	q 1, n	q 0, n	qn	f n
1	0.167	0.833	1	0
2	0.167	0.833	1	0
3	0.162	0.833	0.995	0.005
4	0.162	0.830	0.992	0.003
5	0.161	0.425	0.586	0.406
6	0.094	0.421	0.515	0.071
7	0.082	0.362	0.444	0.071
8	0.072	0.305	0.377	0.067
9	0.061	0.249	0.310	0.067
10	0.050	0.194	0.244	0.066

очевидно, что q Ц - q 0ln - 2 q ^¹ ) , и для q ^¹ ) получается соотношение приведенное в [3]:

1-i \k qn1)-£kl qn .           (4)

k - 1 V ² У

Такое свойство хвостов распределения времени возвращения q_n ^{( l )} обусловлено тем, что события, удовлетворяющие условию { L * <  1 } образуют эргодическое множество состояний. Событие { L n - 1 }, соответственно, является поглощающим состоянием, и процесс формирования последовательности можно представить в виде ориентированного графа. Например, для комбинированной серии длиной l= 4 граф имеет вид, показанный на рис. 1. Вероятности перехода, изображенные на графе стрелками, стационарны и равны p , если последовательность оканчивается “1” (успех), либо 1-p , если последовательность оканчивается “0” (неудача).

Соотношение (3) с учетом (1) позволяет получить исчерпывающую информацию как о T_l , и о L_n . Как показывают исследования с помощью производящих функций, числовые характеристики времени возвращения вычисляются наиболее просто. В частности, среднее время возвращения серии успехов

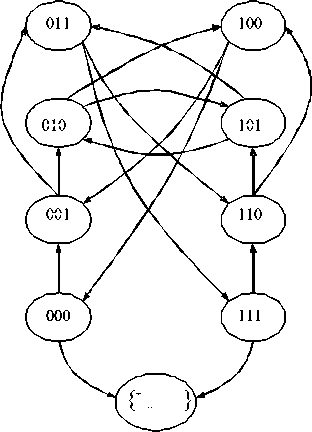
{ L n - 4 }

Рис. 1. Граф вероятностной цепи формирования знаковой серии l=4 (трендовой серии l=5)

длинной 1 при Р ^- 2

составляет

м[т]-Ml - 2.(21 -1).

Среднее время возвращения комбинированной серии при тех же условиях составляет м₁ - 2 ¹ - 1.

В рассматриваемой постановке задачи ис- комыми являются средние значения С В Ln , свя- занные с вероятностями qn(l) соотношением:

n

^{м [} L n ^{] -} * ^-Е ^ *¹ ) .         (5)

1 - 2

Вид точной зависимости M [Ln ] для частного случая (4) в сравнении с результатами имитационного статистического эксперимента представлен на рис. 2. Экспериментальные точки на графиках рис. 2, 3 представляют собой средние по 200 реализациям значения Ln в последовательной выборке X,, i - 1, n из совокупности N(0;1) , а также в последовательностях

1 ⁿ

Y ^- Xi —^ Xi , i - 1, n n i - 1

и Z , - X , _{+ 1} - X , , i - 1, n - 1. Дисперсия при _n ® 50 практически стабилизируется на постоянном уровне (рис. 4). Общий вывод заключается в том, что с ростом n закон распределения L_n быстро выходит на установившийся режим, то есть среднее значение смещается вправо с логарифмической скоростью, а форма рассеяния и, соответственно, ширина интервала рассеивания сохраняются практически неизменными. Границы 90% доверительных интервалов L_n для _{n -} 2 ^ 1000 приведены в таблице 3 (в скобках даны границы 95% доверительных интервалов). Фактически, поскольку СВ L_n целочисленная, речь идет не об интервале в привычном смысле, а о конечном множестве “практически реализуемых” значений. Мощность этого множества практически не зависит от n и составляет 7ч8 и 3ч4 для серий первого и второго типа соответственно. На-

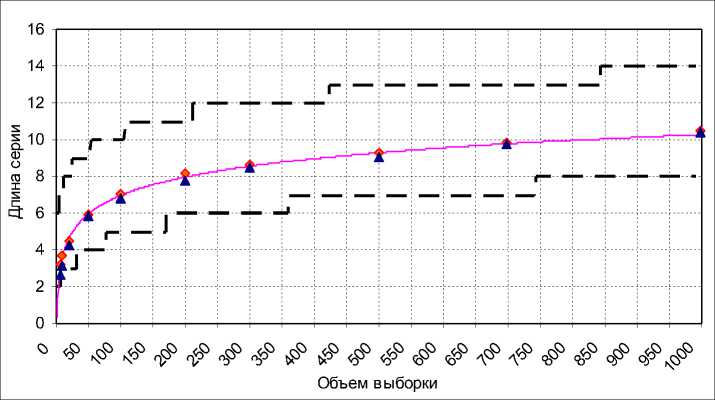
Рис. 2. Среднее значение и границы доверительного ( у >  0,9 ) интервала длины максимальной “знаковой” серии:

- экспериментальные значения в исходной выборке;

▲ - экспериментальные значения в центрированной выборке

пример, требуется найти 90% доверительный интервал для Ln при n = 40. По таблице находим 4 < Ln < 9. Для у = 95% при тех же значениях n интервал составит уже 3 < Ln < 10. При значениях n > 1000 для определения границ доверительных интервалов можно пользоваться простым соотношением 5л _            5л log2 5n - 2,5 < l < log254n + 4,5.

Таким образом для серий в случайной последовательности, к которой применима схема Бернулли, можно считать полностью установленными законы распределения как числа серий [3], так и длины максимальной серии.

Однако существует необходимость теоретического уточнения, обусловленная тем, что рассматриваемая чаще всего на практике 1n последовательность Y = Xi    XXi не яв- n i=1

бой из миноров порядка n _— 1 представляет собой блочную матрицу:

Г n — 1

K = * ² -

1 n

n — 1

n

n — 1

ляется независимой [3]. Значения Y _i связа-

n ны очевидным соотношением X Y = 0• По-=i этому число степеней свободы в ней составляет n — 1. Такое же значение имеет ранг ковариационной матрицы у. При этом лю

1 n

" n — L n > 2.

В дальнейшем, без ограничения общности, дисперсию можно положить равной 1.

Определитель такой матрицы равен

I K_n I = n . Обратная матрица имеет аналогичный вид. На главной диагонали стоят “2”, на остальных местах – “1”.

Например, для n = 5 матрицы выглядят следующим образом:

/

	5	5	5
	1 —	4	1 —
А, г —	5	5	5
5	1	1	4
	5	— 5	5
	1	1	1

⁵ 1

5 7

I 5    5    5

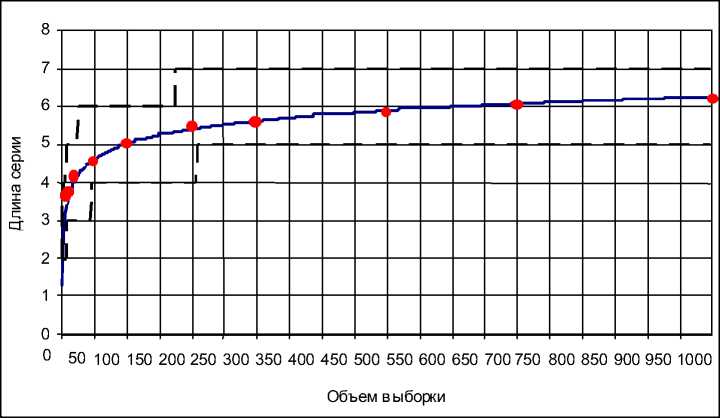
Рис. 3. Среднее значение и границы доверительного интервала ( у >  0,9) длины максимальной “трендовой”’ серии:

- результаты эксперимента

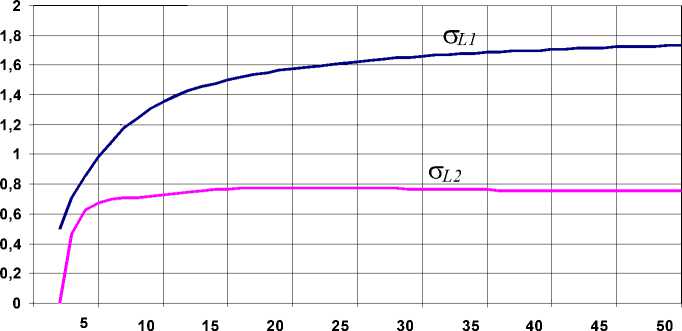
Объем выборки

Рис. 4. Стандартное отклонение длинны максимальной серии в зависимости от объема выборки.

' 2 111 ^ 12 11 112 1 .

. 1 1 1 2 _?

Таким образом, плотность совместного распределения подгруппы любых n - 1 из n величин Y i при нормальном исходном распределении составит:

K ₅ ^{- 1}

Для сравнения, ковариационная матрица последовательности X единичная n x n , а плотность совместного распределения равна:

f ( x ₁, x ₂

x n ) = ^T

(2 π ) ²

1^ exp ^-tE _ ² i = 1

n

x i ²

n

f(yi>y2>->y_n -1) =

— exP

(2 п ) ²

n - 1        n - 2 n - 1

Z y+ZZ yy,

i = 1          i = 1 j = i + 1

n >  3 .                   ⁽⁶⁾

n >  1 .

Принципиальное отличие последовательности Y заключается в том, что размерность пространства элементарных событий составляет не 2ⁿ , а 2ⁿ - 2 , и имеет место отрицательная корреляция [3]. При этом среднее и дисперсия статистики L_n в последовательности Y имеют несколько меньшие зна-

чения. Однако доверительные интервалы L_n уже не будут сильно отличаться от аналогичных интервалов для последовательности Х, поскольку количественное различие между законами распределения быстро сходит на нет с ростом n . Например, для любых двух значений Y при объеме выборки n справедливы следующие соотношения:

P{Y_i >  0, Y >  0} =¹ —- arctg . ¹ , j 4 2 n ⁵ V n ( n - 2) .

P{Y > 0, Y < 0} =1 + — arctg . 1

j 4   2 n       _xn ( n - 2) .

Следовательно, при _n >>  l вероятности в последовательности Y отличаются от аналогичных в последовательности X на вели-

чину порядка ^~ _n .

Средние по 200 реализациям значения

L_n в последовательности Y показаны маркерами ▲ на рис. 2.

При исследовании закономерности образования “трендовых” серий используем тот факт, что соотношение порядка между независимыми выборочными значениями непрерывной С.В. инвариантно к закону ее распределения.

Как известно, в общем случае закон распределения непрерывной СВ F X (x) = P { X <  x } представляет собой монотонно возрастающее (монотонно не убывающее) отображение некоторого подмножества числового интервала (-?;+?) на отрезок [0;1]. При этом очевидно, что из всего многообразия законов распределения существует единственный - R [ 0; 1 ] , который отображает выше указанный отрезок сам на себя. Именно на этом факте построены критерий согласия А.Н. Колмогорова и критерий принадлежности двух выборок одной генеральной совокупности Н.В. Смирнова.

В силу своей универсальности (преобра-

яет на соотношение порядка), закономерность образования трендовых серий является, в некотором смысле, одним из фундаментальных количественных соотношений в материальном мире и, поэтому актуальна для всех без исключения массовых случайных явлений.

Из этих рассуждений общего характера, тем не менее, можно вполне обоснованно сделать конструктивное и весьма существенное заключение, что не ограничивая общность результатов и выводов, достаточно рассмотреть закономерность “трендовых” серий в случайной выборке из совокупности R [ 0;1 ] , сведя тем самым к возможному минимуму объем вычислений (при любом объеме выборки плотность совместного распределения = 1).

Используя принятую в [3] мнемонику, а именно, обозначая “0” отрицательные значения последовательных разностей, “1” – положительные, вероятность любого отрезка последовательности теперь однозначно определится следующим образом:

1         x n            1               x 4         1         1

P { 001...01 } = J dx n J dx n _{- 1} J dx n _{- 2}... J dx 3 J dx ₂ J dx 1 .

n - 1            ^{0        0          x}n - 1             ^{0        x} 3       ^x 2

Например, сравнивая с вычисленными

в [3] ^P { 00 } = 6

P {01}=3,

для выборки из

нормальной совокупности убеждаемся в их совпадении с выборкой из R [ 0;1 ]:

P {00} = J dx3 J dx2 J dx1

0      x3      x2

1       x 3        1

P {01} = J dx3 J dx2 J dx1 =

0      0      x2

1n зование Y = Xi   ^ Xi n i=1

так же никак не вли-

6 ^,

Рассмотрим более детально структуру этих вероятностей. Каждая из них может быть представлена в виде:

P = J ^ (x )dx

где ф (х) - степенной многочлен, порядок которого на 1 меньше длины последовательности. В свою очередь, каждый такой много-

член однозначно определяется набором (вектором) своих коэффициентов.

Используя уже рассмотренную схему рассуждений, разложим вероятности q_n ^{( l )} трендовых серий и, следовательно, соответствующие многочлены, на сумму двух слагаемых. Для наиболее интересного симметричного случая 1 0 = 1 1 система рекуррентных уравнений будет иметь следующий вид:

^{( 1}₌[ ,„( ¹ )       д+ ГГ ,-₉^{( 1} )                  X X ¹ )

^ф 1, n ^{( f} ) J ^ф 0, n - 1 ^{( f} ) ^{df +} J J ^ф 0, n - 2 ^{df +} • • ⁺ J "  • J ^ф 0, n — 1 + 2 ^{( f} ) ^df

0                       0 0                         00

'

1 - 2

1           1111

m(1) (=    (1) (x\dx +      (1) dx + +Г f (1)

ф0,n (f ) J ф1,n-1 (f )df + J J ф1,n-2 df + • + J • J ф1,n-1+2( f )df, x               xxx x

-------V

1 - 2

(l)( ф 0,1 (f) ф1,1 (f ) — 1 .

xxx

(l)                       (l)( фП )(X) = J Vn-1 (X)dx + • + J ...J Vn-1+2 (x)dx,

^——^V— *

I - 2

Из условия симметрии с очевидностью следует, что ф 0 ¹ П ( x ) = V v¹ (1 - x ) • Таким образом, система (8) фактически сводится к одному уравнению:

ф 2 ¹ ) ( x ) = ..ф — ) ( x ) = x ,         (9)

где обозначено      фП 1)( x ) = ф\,zn)( x ), v П,)(x) = фП 1 )(1 - x )•

Порядок рекуррентного многочлена ф П ¹ ) ( x ) равен n - 1, а его коэффициенты имеют вид правильных простых дробей.

Например, при 1 = з рекуррентное уравнение имеет первый порядок:

x

V n ( x ) = J V n - 1 ( x ) dx , п >  3

<            0                      .(10)

V ₂ ( x ) = x .

Откуда получаем:

ф з ( X ) = X - ¹ X ²; ф 4 ^{( x} ) = ^{1 x} - ^{1 x 3};

1       13

ф 5^{( x} ) = з ^{x -} 6 ^{x +} 24 ^x ;

5        13

ф ( X ) =

• 6      24    12     120

16       1   3     1    5     1

ф ₇ ( x ) =---- x--x +-- x--x ;...

• 7     120   18     120720

Соответствующий ряд вероятностей, оп- ределяемых как ^П1 = 2J фп3(x)dx,составит:

2 5 16 61 272

3 ;…

12 60 360 2520

При 1 = 5 порядок рекуррентного уравнения составляет l- 2=3:

x           xx            xxx

Ф п ( X ) = J Ф п - 1 ( X ) dx + J J Ф п - 2 ( x ) dx + J J J Ф п - з ( x ) dx , n >  5

0           00            000

ф 2^{( x} ) = V з^{( x} ) = V 4^{( x} ) = ^x

Последовательность многочленов и ве-

роятностей q_n ⁽⁵⁾ составляет:

V 5 = ^x

—

1 4 x

24 ;

ф = —X +-- X

⁶    24    12

—

x

—

1 _x 5 ;;

ф = —X +-- X

⁷    12    16

—

1 _x 3

—

1 _x 4

(5)    59 349

q () =—;— n 60 360

;

2520 ;...

Общий вид формул для рекуррентного многочлена, рекуррентных соотношений для его коэффициентов и вероятностей q_n ^{( l )} выглядит следующим образом:

п - 1

ф П^{1 )(} X ) = 2 a k^{1 )( п} ) X ^k , ^п > ¹

к = 1

a k 1 ) ( п ) = ™"( k;1 - ^{2) ( —}1) k ^- i ^{( к —} i ^)!

i = 1

„ ( 1 ) = 2 ^ ^1 a к¹ )^{( п} ) .q^{n     z} к + 1

k !

п - i - 1

z C m ^- i am' )^{( п —} i ), ^п > ¹ , ^к - ^{п — 1} m = к - i

Точные значения M [ L_n ] и < 7 ^ трендовых серий в сравнении с результатами статистического эксперимента приведены на рисунках 3, 4. Границы доверительных интервалов для L_n трендовых серий указаны в табл. 4. Устройство и порядок работы с ней

Таблица 3

Объем выборки, n	M[L2n]	σ L 2	НГ	ВГ
2	2,00	0,00	2	2
3	2,33	0,47	2	3
4	2,67	0,62	2	4
5	2,90	0,68	2	4
6	3,08	0,70	2	4(5)
7	3,22	0,71	2	4(5)
8	3,33	0,71	2	5
9	3,42	0,72	3(2)	5
10	3,50	0,73	3(2)	5
12	3,63	0,75	3	5
14	3,74	0,76	3	5
16	3,83	0,77	3	5
18	3,92	0,78	3	5(6)
20	3,99	0,78	3	5(6)
25	4,14	0,77	3	5(6)
30	4,27	0,77	3	6
40	4,45	0,76	3	6
50	4,58	0,76	4	6
100	4,99	0,76	4	6(7)
200	5,39	0,73	4	7
300	5,61	0,72	5	7
500	5,88	0,73	5	7
700	6,06	0,71	5	7(8)
1000	6,25	0,69	5	7(8)

Таблица 4

Объем выборки, n M[L1n] σL1 НГ ВГ 2 1,50 0,50 1 2 3 2,00 0,71 1 3 4 2,38 0,86 1 4 5 2,69 0,98 1 5 6 2,94 1,09 2(1) 5(6) 7 3,16 1,18 2 5(6) 8 3,34 1,25 2 6 9 3,51 1,30 2 6(7) 10 3,66 1,35 2 6(7) 12 3,92 1,43 2 7 14 4,15 1,48 2 7(8) 16 4,34 1,52 3(2) 7(8) 18 4,51 1,55 3(2) 7(8) 20 4,66 1,58 3 8 25 4,98 1,63 3 8(9) 30 5,24 1,66 3 8(9) 40 5,66 1,70 4(3) 9(10) 50 5,98 1,73 4 9(10) 100 6,98 1,79 5(4) 10(11) 200 7,98 1,83 6(5) 11(12) 300 8,56 1,84 6 12(13) 500 9,30 1,85 7 13(14) 700 9,78 1,86 7 13(14) 1000 10,30 1,86 8 14(15) полностью аналогичны табл. 3. Например, при объеме последовательной выборки количественных данных (результатов измерений) n = 100 максимальная длина монотонно убывающей или возрастающей последовательности (трендовой серии), согласующаяся с гипотезой об отсутствии закономерно обусловленной изменчивости, должна лежать в границах 4 < L100 < 6 при уровне значимости 1 - y = 10%. При уровне значимости 1 - y = 5% интервал составляет 4 < L100 < 7.

Таким образом, закономерность формирования трендовых серий имеет качественно сходный характер со знаковыми, а именно, среднее значение длины максимальной серии с увеличением n неограниченно возрастает. Аналогичным образом ведут себя и границы интервала рассеивания, причем, ширина интервала остается практически постоянной. Различия заключаются в том, что среднее значение с увеличением n растет не как двоичный логарифм, а существенно мед- леннее – как обратная гамма-функция: n * Г (M [Ln ] +1). При этом интервал ее рассеяния примерно вдвое уже, чем знаковой: Г-1( n) - 2 < l < Г-1( n) +1.

Полученные ассимптотические оценки средних значений длины максимальной серии являются эмпирическими. Однако они дают поразительно высокую точность, по крайней мере, в исследованном диапазоне _n <  10 5 . Последнее обстоятельство, конечно же, не лишает актуальности задачу их строгого аналитического исследования, также как и числовых характеристик более высокого порядка. Тем не менее, как представляется, есть основания полагать, что установленные закономерности, главным образом механизм формирования последовательности в немарковской цепи (с зависимыми вероятностями перехода), являются нетривиальным теоретико-вероятностным результатом и могут найти интересные приложения в смежных с теорией вероятностей областях.

Кроме того, учитывая разработку критерия длины максимальной серии до простой в обращении типовой методики, представляется возможным и целесообразным, чтобы этот критерий был включен в инструментарий специалистов, занимающихся статистическим анализом в прикладных исследованиях.