Закон распределения Пуассона в российской космической отрасли

Авария ракеты-носителя "Протон-М" с мексиканским спутником MexSat-1, случившаяся 16 мая 2015г., стала последней каплей в череде неудач российской космической отрасли последних трех лет. Общественность и пресса сошлись в крайне негативной оценке работы специалистов «Роскосмоса». Реакция же российского правительства оказалась вовсе бескомпромиссной – в космическом агентстве началась глобальная реорганизация, весь управленческий состав был освобожден от занимаемых должностей, процесс изготовления ракет решено фиксировать на фото и видео, а уникальные спутники перед запуском на орбиту теперь обязательно требуется застраховывать.

Однако серия неудач с орбитальными пусками российских космических аппаратов может быть связана не только с техническими проблемами российской сборки или с неэффективным управлением. В данной статье предлагается построить математическую модель падения ракет и с помощью нее статистически проанализировать сложившуюся ситуацию.

На первом этапе исследования необходимо проверить являются ли результаты запусков случайными величинами, естественно распределенными по определенному закону, допускающему какие-либо редкие значительные отклонения, которые на первый взгляд кажутся аномалиями. Если это так, необходимым является определить, какой именно это закон распределения.

Если предположить, что вероятность падения ракеты p является ни от чего не зависящим случайным событием, общее количество падений k за n запусков подчиняется биноминальному закону распределения:

Р(к,п) = Ckpk(1-P)n-k

Число сочетаний С в этой формуле при больших n слишком сложно для вычисления, поэтому применим другой закон распределения ─

Пуассона, который дает аналогичные результаты при 0,1 <  пр < 10:

Р(к, п)

Л.к * е ^ к!

Параметр . = пр    здесь является средней интенсивностью рассматриваемых событий.

Для анализа авторов были взяты результаты всех орбитальных запусков, произведенных в СССР и России, за период с начала 1980 года по конец прошлого, 2015 года (рис. 1). В исследовании были использованы данные официальных источников, таких как Федеральное Космическое Агентство, центр обработки и отображения полетной информации.

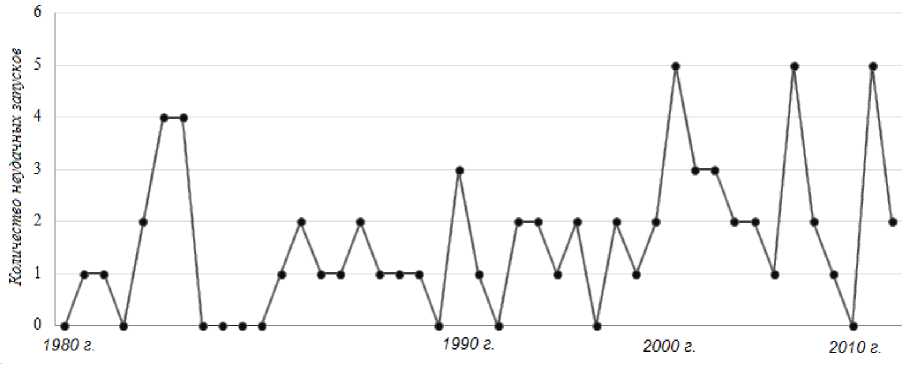
Рис.1. Количество неудавшихся запусков отечественных ракетоносителей

При этом запуски ракетоносителей сгруппированы не отдельно по каждому году, а объединены в группы по 40 запусков (среднегодовое

число запусков за все время). Это сделано для того, чтобы данные представляли собой выборки из одной и той же генеральной совокупности, распределенные по закону распределения Пуассона с фиксированным параметром Л = Tip.

Сравнение реальных данных и рассчитанных по формуле 1 представлены в таблице 1. За этот период средняя интенсивность космических инцидентов для отечественных ракетоносителей составила Л = 1,605 на каждые 40 запусков. Данное число означает, что из 40 запусков космических аппаратов в среднем 2 запуска будут являться неуспешными. По подсчетам за аналогичный период статистика NASA1 оказалась куда печальнее (Л = 2,303).

Таблица 1. Сравнение фактических данных и случаев, предсказанных по Пуассону

Количество неуспешных запусков (k)	Наблюдаемые случаи	Случаи, предсказанные по Пуассону
0	10	8,64
1	13	13,87
2	12	11,13
3	3	5,95
4	2	2,39
5	3	0,77
6	0	0,20
7	0	0,05
8	0	0,01
9	0	0,00
10	0	0,00

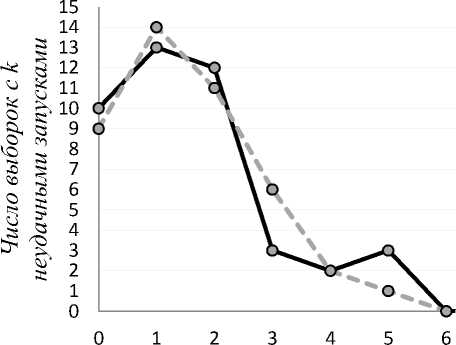
Заметно, что предсказанные и фактические значения хорошо коррелируются. Что свидетельствует, во-первых, о том, что аварии при запусках действительно распределены во времени по закону Пуассона, а во-вторых, что серия космических неудач последних лет, вероятно, является всего лишь не самым лицеприятным экземпляром выборки, без наличия которой это бы уже не было распределением Пуассона (рис.2).

- -о - -о - -о - -о

7     8     9    10

Количество неудачных запусков k за выборку

Рис.2. Сопоставление наблюдаемой статистики и ряда распределения Пуассона

Проверим данное утверждение статистически с помощью критерия согласия Пирсона у2, который предназначен для проверки гипотезы о законе распределения значений признака X в генеральной совокупности. Выдвинем гипотезу о соответствии распределения числа неудачных запусков закону Пуассона. На уровне значимости 0,1 имеем:

Реальные данные

Предсказаные по

Пуассону

Унабл « /2рит (8,376 « 14,684), что говорит о том, что гипотеза не отвергается и подтверждает правильность наших предположений.

Таким образом, с большой долей вероятности можно утверждать, что число неуспешных запусков в космос подчиняется распределению Пуассона, которое представляет собой результаты, которые можно было бы ожидать, если принять падение спутников как чисто случайный процесс. Поэтому сложившаяся ситуация в российской космической отрасли может объясняться существованием порядка и закономерности в явлениях, которые считаются результатом целесообразной деятельности человека.