Закон сохранения мощности в двойственных тензорных сетях Г. Крона - А. Петрова (в пространстве, времени и структуре)

Наблюдаемый мир есть пространство и время. Пространство существует само по себе, независимо от расположенных в нем материальных объектов. Звезды, межзвездный газ, другие материальные объекты занимают лишь ничтожную часть наблюдаемого объема пространства. Возникающие из сопоставления астрономических наблюдений и теоретических расчетов понятия темной материи и темной энергии указывают на существование других физических объектов в пространстве или вне пространства. Причем количество ненаблюдаемых (темных) массы и энергии многократно превосходит количество наблюдаемого вещества и энергии.

Мы наблюдаем не все окружающее нас пространство. Такие основания дают законы структуры, связей объектов, расположенных в пространстве. Изменению структуры соответствует закон сохранения потока энергии. Поток энергии в структуре пространства расщепляется между двумя сетями с двойственной структурой. Только тогда он остается постоянным при изменении структуры потоков в сети.

Структура в пространстве образована совокупностью открытых путей и замкнутых путей, которые двойственны и ортогональны друг к другу. Каждому замкнутому пути в одной сети соответствует открытый путь в двойственной сети, и наоборот. Двойственность является свойством пространства, так же как однородность и изотропия.

Замкнутая система не взаимодействует с окружающей средой. Величины определяются через измерение расстояния и длительности (времени).

Однородность пространства дает постоянство импульса при движении замкнутой системы материальных точек. Изотропия пространства дает постоянство момента импульса при движении замкнутой системы материальных точек.

Поступательному движению соответствует закон сохранения импульса. Это предполагает, что при переходе от одной точки пространства к другой не происходит изменений, пространство однородно.

Вращательному движению соответствует закон сохранения момента импульса. Это предполагает, что при переходе от одного направления пространства к другому не происходит изменений, пространство изотропно, однородно по всем направлениям.

Поток энергии, измеряемый мощностью (энергия в единицу времени), остается постоянным в замкнутой системе, состоящей из двух двойственных сетей. По своей физической сути это закон сохранения потока энергии для двух двойственных электрических цепей. Суммарная мощность постоянна при изменении структуры соединения ветвей двух двойственных сетей.

Понятия открытого и замкнутого пути существуют сами по себе, независимо от того, являются ли они носителями движения. В пространстве есть замкнутые и открытые линии, т.е. последовательности множества точек. Это не всякие точки, а прилегающие друг к другу точки, составляющие линию, и точек этих в линии бесконечность. Линии также покрывают все пространство во всех направлениях. Число направлений столь же бесконечно, что и число точек. Можно их мыслить как не связанные с числами, не оцифрованные.

Простейшей сетью является структура орбиталей атома. Свободные электроны являются элементами электрического тока. Они могут двигаться в любом направлении, их движение можно разложить на поступательное и вращательное. В атоме движение электронов вращательное. При этом вращении (как частицы, или как облака вероятностей) не расходуется энергия. Как и при вращении планет вокруг звезды.

Пространство

Пространство есть совокупность вещей, называемых точками, линиями, поверхностями, объемами. А также в пространстве есть углы, направления, расстояния и т.д., писал Фридман [1, с. 17], ссылаясь на Гильберта. Пространство обладает свойствами непрерывности заполнения одинаковыми точками, гладкости, метрики (расстояния), направления. Точки плотно заполняют пространство, между ними не должно быть «пробелов». Это означает, что между любыми, сколь угодно близкими точками существует бесконечное количество точек, не меньше, чем в остальном пространстве. Говорят об окрестности точки – это множество, содержащее данную точку, и близкие (в каком-либо смысле) к ней. Понятие «между» предполагает наличие направления от одной точки к другой. Это направление называют линией; таких линий может быть бесконечно много.

Все точки одинаковы (однородность). Все направления одинаковы (изотропия).

Арифметизация (цифровизация) пространства

Для описания пространства необходимо установить соответствие между его точками (или другими объектами) и числами, провести «арифметизацию». Между любыми вещественными числами находится бесконечное количество рациональных чисел; этим обеспечивается всюду плотность чисел. Множество чисел и множество точек имеют равную мощность в смысле теории множеств. Это и позволяет каждой точке поставить в соответствие число или набор чисел. Размерность пространства – это количество чисел, которое необходимо, чтобы определить каждую точку. Переход от одного способа арифметизации пространства к другому способу арифметизации называется преобразование координат. Арифметизация (цифровизация) необходима для описания материальных объектов, занимающих часть пространства. Если материальный объект занимает часть пространства, то другой объект не может занимать эту часть пространства.

Человек не видит того, что он не может назвать. Мир существует без чисел, без арифметики, которая устанавливает отношения между числами, а также без систем отсчета и другой математики. Чтобы отобразить мир, исследовать его и преобразовать, человек должен назвать его (в целом и по частям), например, дать точкам имена. Наиболее удобные имена для точек – это числа. «Установление правил, пользуясь коими можно по данному свойству класса отыскивать соответствующее ему число, (или пару, или тройку чисел) и по данному числу… отыскивать отвечающее ему свойство класса, назовем … арифметизацией данного класса» [1, Фридман, 1965, с. 11]. Таким образом, оцифровывание, или арифметизация мира состоит в том, что всем точкам присвоены имена, числа.

Размерность пространства указывает, сколько нужно задать независимых чисел, чтобы однозначно определить единственное «имя» точки. Порядок следования чисел друг за другом дает способ описания точек мира, следующих одна за другой. Это и позволяет выделить линии для различения их друг от друга.

Обозначение точек числами еще не означает измерения, пока не определено понятие больше или меньше для положения точки в пространстве. Для определения отношения между двумя точками вводят понятие расстояния, т.е. степень их удалённости друг от друга. Чтобы найти расстояние между точками, надо произвести измерение. Для этого необходимо ввести линию (координату), вдоль которой проводится сопоставление измеряемых объектов, а также задать единицу измерения. Таким образом, для измерения необходимы четыре точки: две точки начала и окончания единицы измерения, и две точки начала и окончания измеряемого объекта.

Линии (структура) и расстояние (метрика)

Линии выделяют одни участки пространства среди остальных участков пространства, т.е. задают некоторую структуру . В геометрии возникает вопрос сравнения между собой линий, прямых и не прямых, которые связывают две точки.

То, что линия соединяет две точки, не определяет величину расстояния между точками. Об этом писал Кант. «Что прямая линия есть кратчайшая между двумя точками, это - синтетическое положение, так как мое понятие прямого не содержит ничего о величине, а содержит только качество. Понятие кратчайшего, следовательно, целиком прибавляется, и никаким расчленением не может быть извлечено из понятия прямой линии. Здесь, следовательно, необходимо прибегнуть к помощи созерцания, посредством которого только и возможен синтез» [3, с. 83]. В механике связь понятий «прямая» и «кратчайшее» выражает принцип наименьшего действия, который принимают за постулат.

Понятие расстояния между точками представляет собой меру, метрику, а понятие прямой линии между точками - это структура связей между ними. Эти понятия не выводятся друг из друга, а являются независимыми качествами . В математике метрика и структура представляют собой два независимых понятия. «Когда графы дополняются импедансами, аппарат комбинаторной топологии должен быть дополнен аппаратом теоретикомножественной топологии» [6, с. 17]. Метрика определяет меру связи между воздействием и откликом в поведении систем, потоки в элементах, но не использует структуру. Структура описывает способы соединения элементов систем, но не рассматривает метрику. Тензорный анализ сетей, предназначенный для проектирования инженерных систем, описывает изменение процессов при изменении структуры.

Произвольность арифметизации (введения системы отсчета) как пространства, так и времени, показывает, что их собственные свойства инварианты по отношению к изменению системы отсчета, не зависят от выбора системы отсчета. Например, расстояние между точками является собственным свойством пространства. Расстояние является функцией координат точек, и эта функция зависит от выбора координат. Когда эта функция получена, то говорят, что метрика пространства определена. Определить метрику для другого способа арифметизации можно с помощью преобразования координат [1, с. 13].

В декартовых координатах расстояние между точками Р и Р' равно корню из суммы квадратов разности их координат (обобщенная теорема Пифагора). Положим, что расстояние не зависит от порядка следования точек (Р, Р`) = (Р`, Р) , а расстояние двух точек с одинаковыми координатами равно нулю (Р, Р) = 0 . Рассмотрим квадрат расстояния ds двух достаточно близких точек. Разложим его, например, в двумерном пространстве, в ряд Тейлора по степеням разности координат двух точек ( x_i, x₂ ) и ( x' i , x₂' ) [1].

(ds)² = g o + g i ( x' i - X i ) +g 2 ( x' 2 - X 2 ) +

+ g ii ( x' i - x i ) 2 +g i2 ( x' i - x i ) ( x' 2 - x 2 ) + g 2i ( x' 2 - x 2 ) ( x' i - x i ) + g 22 ( x' 2 - x 2 ) ² + ...

Из второго условия следует, что g 0 = 0, а из первого условия следует, что g 1 = g 2 = 0. Тогда, обозначая d 1 = ( x` 1 – x 1 ) и d 2 = ( x` 2 – x 2 ), получим:

(ds)² = g 11 d 1 ² + g 12 d 1 d 2 + g 21 d 2 d 1 + g 22 d 2 ² + … = g 11 d 1 ² +2 g 12 d 1 d 2 + g 22 d 2 ² + …, где коэффициенты g ik являются функциями координат точек двумерного пространства, и представляют собой компоненты метрического тензора. Пренебрегая в этом разложении степенями более высоких порядков, получаем четыре компоненты. Эти компоненты образуют матрицу четыре компоненты. Метрика показывает меру, качество измерения линии между двумя точками. Для трехмерного пространства метрический тензор состоит из шести функций координат точки, и т.д. Метрику вводят через понятие расстояния. Г. Вейль в 1931 г. также вводил метрику «посредством нового фундаментального понятия: абсолютной величины вектора», т.е. расстояния [14]. Интересно, что Вейль вводит понятие двойственного пространства через скалярное произведение, но это пространство имеет такую же размерность, как первичное пространство. При изменении структуры размерность пространств замкнутых и разомкнутых путей меняется.

Квадрат расстояния между двумя точками получили как сумму квадратов разностей координат этих точек, так что он является положительно определенной функцией. Само расстояние может иметь ориентацию, знак которой зависит от порядка прохождения точек; на величину квадрата расстояния это не влияет.

Плотность заполнения пространства

Пространство плотно заполнено точками без пробелов. В пространстве есть тела (объекты). Положение объекта – это место, те «точки» пространства, которые занимает объект. Другой объект не может занимать это место.

Принцип Паули (принцип запрета) утверждает, что в атоме в одном и том же квантовом состоянии может одновременно находиться один электрон. Это состояние характеризуют четыре квантовых числа: главное, орбитальное, магнитное и спиновое. Каждому состоянию соответствует своя орбита с определенной энергией, свое «место», которое занимает электрон. Другой электрон должен отличаться значением хотя бы одного квантового числа; этому соответствует другая энергия. Электроны заполняют последовательно квантовые состояния с наименьшей суммарной энергией, которым соответствуют орбиты электронов (орбитали) в атоме. Это означает, что если орбиталь занята электроном, то другой электрон туда попасть не может, эта часть пространства занята.

При этом в атоме возникают электронные оболочки на определенном расстоянии. Связано ли это с порциями энергии электронов, или таково свойство структуры пространства? Что задает в природе ритмы квантования?

В солнечной системе материя сложилась в планеты, они вращаются на определенных расстояниях от светила. Эти расстояния пропорциональны частотам звуков в октавах музыкального ряда. Формы рельефа Земли (трещины, долины, хребты) подчиняются ряду дискретных размеров, определенной структуре. В обществе также сначала заполняются уровни с наименьшими способностями, над которыми возникают уровни с талантами. Лидер должен опираться на достаточное количество более слабых людей.

Принцип Маха утверждает, что существование пространства и времени неразрывно связано с существованием физических тел. Удаление всех физических тел должно прекращать существование пространства и времени. А что же тогда было до Большого взрыва, и где он происходил, и в какое время? Заполненное физическими телами пространство не оставляет возможностей для движения, которое состоит в изменении положения тел в пространстве. Звезды и другое вещество заполняют ничтожную часть пространства. Пространство существует независимо от материальных, физических тел, которые в нем расположены. Опыты с ядром лития показали невыполнение принципа Маха.

Время

Время есть число движения.

Аристотель

Время определяется как набор точек на некотором основном движении. Фридман называет это часами данной точки. Время необходимо для описания движения в пространстве, которое состоит в изменении положения точки, характеризуемое изменением ее координат. Пока все точки находятся на своих местах в пространстве, время не нужно. Без движения время не имеет смысла. Когда точки изменяют свое положение в пространстве, нужно описать различие между началом и концом движения, а также промежуточные положения точек при переходе от начала движения до его окончания.

Выбор физического местного времени соответствует произвольности арифметизации представляющего его «одномерного пространства». Замена одного времени на другое будет различным в разных точках пространства, т.е. преобразование времени связано с пространством. Собственные свойства физического времени должны быть инвариантны относительно таких преобразований. Таким собственным свойством является промежуток между двумя моментами (точками) времени, что аналогично понятию расстояния в пространстве.

Измерение времени

Начало отсчета и масштаб измерения времени можно установить достаточно произвольно. Аврелий Августин Иппонийский писал в 4-м веке, что время обладает длительностью, которая характеризует продолжительность всякого движения и изменения, но определить его можно по-разному. «… Если бы, действительно, все светила небесные остановились, а какое-либо колесо гончара продолжало бы вращаться, разве тогда не было бы времени, при помощи которого мы стали бы измерять обороты этого колеса? Мы бы сказали, что обороты происходят или в одинаковые промежутки времени, или … что одни длятся дольше, а другие меньше? … Светила небесные – это знаки, определяющие время, годы, дни; это правда, но, остерегаясь сказать, что оборот деревянного колеса – это и есть день, я все-таки не стал бы спорить, что это не время. Пусть же не говорят мне: время – это движения небесных тел. Когда, по молитве, солнце было остановлено, чтобы человек мог одержать победу, то солнце стояло, а время шло». Эту цитату приводит Фридман [1, с. 54]. В сборнике докладов памяти Г. Крона Э. Тоулан пишет, что сказал Крону в дискуссии о времени – следовало бы почитать 11 книгу «Исповеди» Святого Августина. Тот надолго замолчал, заметив потом, что это была хорошая беседа [4].

Точка может двигаться по прямолинейной траектории (поступательное движение) или по круговой траектории (вращательное движение). Любое движение можно разложить на поступательное и вращательное. Отмечая точки на траектории движения можно сопоставить этим точкам отдельные моменты (точки времени) и применять для измерения времени. Движение должно быть равномерным, чтобы равным отрезкам соответствовали равные промежутки времени. Однородность времени нельзя доказать, мы только предполагаем, на основании опыта, что равномерность движения, которое используется для измерения времени, обеспечивает равноправие всех моментов. Кроме того, движение должно происходить на расстоянии, достижимом для измерения. На прямолинейной траектории движение точки постепенно уведет ее так далеко от измеряющего наблюдателя, что сделает измерение практически невозможным. По этой причине для измерения времени используются круговые (вращательные) движения, при которых точка периодически возвращается в исходное положение. Это могут быть вращения звезд по орбитам, или колебания электронов в атоме (вращение по орбитали).

Изменение координат точки может происходить по двум причинам. В одном случае, двигается точка, меняя свое положение в пространстве, меняются ее координаты, а система отсчета неподвижна. В другом случае точка неподвижна, а система отсчета двигается, при этом меняются координаты точки. Это активная и пассивная точки зрения на преобразование координат. Они математически равноправны [11]. В тензорном анализе принимается пассивная точка зрения на преобразование координат.

Таким образом, для измерения расстояния в пространстве между двумя точками используется разомкнутая линия. Для измерения времени (расстояния между двумя событиями) используется замкнутая линия, обороты вокруг некоторой оси.

Движение

Есть пространство и время с их свойствами. В пространстве существуют тела, объекты, которые занимают часть пространства. Занимаемая телом часть пространства может изменяться с течением времени. Тела не являются пространством или временем, но их существование подчиняется свойствам пространства и времени.

Положение объекта, тела в пространстве описывают координаты объекта в заданной системе отсчета. Движение есть изменение положения объекта в пространстве относительно других тел за определенное время. Время определяет скорость изменения положения, т.е. скорость движения.

Какие величины необходимы и достаточны для описания движения? По какому пути происходит движение в пространстве от одной точки до другой точки? Для расчета изменения положения тел делается два предположения о движении.

Первое предположение делается о величинах, которые нужны, чтобы определить и измерить движение. «Одновременное же задание всех координат и скоростей полностью определяет, как показывает опыт, состояние системы и позволяет в принципе предсказать дальнейшее ее движение» [2, с. 10]. Заметим, что это показывает опыт, а не теория.

Оптимальность движения

Второе предположение делается о пути движения. Используется принцип наименьшего действия, или принцип Гамильтона. Он имеет характер аксиомы, и ни откуда не следует. Этот принцип предполагает, что движение из одной точки пространства в другую точку пространства происходит по оптимальному пути. Точнее, принцип состоит в том, что при движении тела из положения Р 1 , заданного набором координат х 1 , в положение Р 2 , заданное другим набором координат х₂ , с момента времени t 1 до момента времени t₂ интеграл S, называемый действием, от функции L , которая зависит от координат, скоростей и времени, принимает наименьшее возможное значение.

5 = J^t2L( q > q, t) dt = min                                                         (1)

Функция L известна как функция Лагранжа. Уравнение об оптимальности движения открывает книгу «Механика» курса Л.Д. Ландау и Е.М. Лифшица «Теоретическая физика».

Действие S – это скалярная величина, которая рассматривается как мера движения физической системы, зависящая от траектории ее движения. Действие представлено как интеграл от функции координат, скоростей и времени. Точка над буквой q означает производную по времени; в данном случае это скорость, обозначаемая обычно v .

Таким образом, движение в пространстве и времени происходит не по любому, а по оптимальному пути. Материальная точка, тело или система движутся по пути, который требует наименьшей возможной энергии. Например, по такому пути, что сумма кинетической и потенциальной энергии по времени движения является наименьшей. Путь является элементом структуры, а тело, которое по нему движется можно рассматривать как элемент потока. Т.е., уже здесь есть понятия структуры и потока.

Уравнения движения

Допустим, что существует функция, для которой действие минимально. Эта функция описывает изменение положения (путь движения) тела. Тогда для другой функции, описывающей движение тела по любому другому пути, действие должно возрасти. Если исходить из самых общих условий, то можно определить вид функции, описывающей движение. Эти условия состоят в том, что: значения всех функций в начале и в конце движения одинаковы, значение интеграла минимально, а пространство и время обладают свойствами однородности и изотропии (равноправны все точки и все направления).

При перемещении тела (системы) в пространстве из одного положения в другое положение разность (вариация) между функцией с минимальным действием, и любой другой функцией, для которой действие возрастает, должна равняться нулю. Далее, например, в [2], разность этих функций разлагают в ряд по степеням координат и скоростей, и приравнивают к нулю члены первого порядка, в соответствии с вариационным исчислением. Вариационное исчисление в общем виде ищет функции, которые минимизируют такие интегралы [11, с. 345]. Затем производится интегрирование вариации, применяется интегрирование по частям. Значения всех вариантов функций описания движения в начале и в конце интервала времени должны быть одинаковы. Отсюда получаем известные дифференциальные уравнения движения, которые в механике называют уравнениями Лагранжа, а в вариационном исчислении – уравнениями Эйлера:

d dL dL

- dt dė    dq

В таком виде уравнения движения не уточняют вид функции Лагранжа, а только связывают обобщенные координаты и обобщенные скорости. Эти уравнения в данном случае представляют интерес в связи с законами сохранения и соответствующими им свойствами пространства.

Фридман начинает рассмотрение пространства, времени и движения с понятия измерения величин. Свойства величин быть больше или меньше называет интенсивностями, для которых определяет понятия начального значения и единицы измерения. А затем уже вводит пространство и его арифметизацию.

Однородность и изотропия

Свойства однородности (равноправия всех точек) и изотропии (равноправия всех направлений) пространства, а также однородности и изотропии времени авторы «Теоретической физики» рассматривают в связи с необходимостью выбора системы отсчета для наиболее простого описания движения. Однако связывают собственные свойства пространства, а именно однородность и изотропию, с выбором системы отсчета, по сути, с позицией наблюдателя.

«По отношению к произвольной системе отсчета пространство является неоднородным и неизотропным. Это значит, что если какое-либо тело не взаимодействует ни с какими другими телами, то, тем не менее, его различные положения в пространстве и его различные ориентации в механическом отношении не эквивалентны. … Оказывается, однако, что всегда можно найти такую систему отсчета, по отношению к которой пространство является однородным и изотропным, время – однородным. Такая система называется инерциальной » [2, с. 13-14]. По отношению к такой системе свободное тело, покоящееся в некоторый момент времени, и далее остается в покое. Вместе с тем собственные свойства самого пространства, например, однородность и изотропия, не могут зависеть от существования систем отсчета, которые вводит наблюдатель.

Инерциальные системы отсчета движутся относительно друг друга равномерно и прямолинейно. Опыт показывает , как утверждают физики, что в инерциальных системах отсчета одинаковы свойства пространства и времени, а также все законы сводного движения. И в этом суть принципа относительности Галилея.

Крон писал, что процессы в системах с разной структурой описывают уравнения поведения одинаковой формы. При этом для описания поведения электрических машин применяются, например, вращающиеся системы координат. К инерциальным системам они не относятся, поскольку движутся не прямолинейно, однако успешно применяются для описания движения электромеханических преобразователей, т.е. электрических машин.

Более того, однородность и изотропия пространства и времени обеспечивает аналогии, одинаковость описания разных предметных областей. «Удивительно, как мало существует первичных типов элементов, образующих строительные блоки огромного разнообразия технических структур… Разнообразие структур отличается только способом взаимных соединений, а многообразие теорий только типом рассматриваемой гипотетической системы отсчета». Г.Крон. «Тензоры для цепей», 1942 г. Впрочем, это отмечалось и ранее. «Единство природы обнаруживается в поразительной аналогичности дифференциальных уравнений, относящихся к разным областям явлений» – В.И. Ленин [7, с. 106].

Если пространство существует, то его свойства однородности и изотропии не могут зависеть от используемых нами систем отсчета. Функция Лагранжа вводится в общем виде, как зависимость от положения (координат), скоростей и времени. Однородность и изотропия пространства и времени позволяют уточнить вид функции Лагранжа. Например, в силу однородности пространства и времени уравнение движения материальной точки не должно зависеть от радиуса вектора, заданного координатами, а также от времени.

Движение не должно зависеть от того, в какой системе отсчета мы его описываем, а также от того, с какого момента начинается отчет времени. Таким образом, в уравнениях движения переменным параметром остается скорость. Поскольку все направления равноправны в силу изотропии пространства, то уравнение движения не зависит от направления вектора скорости, а зависит только от абсолютной величины скорости v . Принято говорить, что от квадрата скорости, v² (а почему не от модуля скорости?). Поскольку функция Лагранжа не зависит от радиус-вектора г , то производная функции Лагранжа по нему равна нулю.

= 2£ = о

dq dr

Тогда и оставшаяся в уравнении движения производная по времени равна нулю:

d dL _ d dL

̇

Отсюда следует, что производная функции Лагранжа по скорости является постоянной величиной ^ = с о nst. «Но поскольку эта производная зависит только от скорости, то отсюда следует, что и v = const, „.приходим к выводу, что в инерциальной системе отсчета всякое свободное движение происходит с постоянной по величине и направлению скоростью. Это утверждение составляет содержание так называемого закона инерции» [2].

Закон инерции существует, но почему из постоянства производной по скорости следует вывод о постоянстве самой скорости? Аналогично можно было бы утверждать, что из постоянства производной скорости по времени следует постоянство времени, но время не постоянно, а речь идет о постоянстве ускорения. Функция Лагранжа для движения свободной материальной точки зависит от квадрата вектора скорости v в любой инерциальной системе отсчета. Опуская детали разложения в ряд по степеням скорости движения одной системы отсчета относительно другой системы отсчета, это можно записать так:

L(v²) = аv² = m v²/2 = T.                                                             (5)

Коэффициент а обозначают ( так принято ) как m/2 , и величину m называют массой материальной точки. Таким образом, масса является следствием однородности и изотропии пространства и времени [2, с. 16]. Иначе в уравнении движения помимо квадрата скорости появились бы другие величины, и другие коэффициенты, соответствующие другим величинам.

Половина, ½, возникает в разных уравнениях описания энергии, что не является случайным, а связано с разделением потока энергии между двумя структурами двойственных сетей. Полученная величина, представляющая вид функции Лагранжа, называется кинетической энергией, она обозначена как T .

О физической размерности величины действия при анализе уравнений движения не делалось никаких предположений. Функции Лагранжа по размерности соответствует энергия, в данном случае, это кинетическая энергия. В нее входит квадрат величины скорости, и коэффициент пропорциональности, который имеет размерность массы. Тогда действие, как интеграл по времени от функции Лагранжа, имеет размерность энергии, умноженной на время.

Взаимодействие частей в системе

Если механическая система состоит из двух частей со своими функциями Лагранжа, то при разведении частей на большое расстояние можно пренебречь их взаимодействием. Таким образом, «уравнения движения каждой из невзаимодействующих частей не могут содержать величины, относящиеся к другим частям системы» [2, с. 12]. Тогда функция Лагранжа всей системы равна сумме функций Лагранжа отдельных частей. Возможность суммирования частей (аддитивность) является важным свойством функции Лагранжа. Аддитивность означает, что величины частей не усиливают влияния частей друг на друга, а просто складываются.

Однако свойство аддитивности выводится из предположения, что не взаимодействуют подсистемы, разведенные достаточно далеко. Но тогда система должна состоять из частей, удаленных друг от друга. А если части системы расположены близко? Тогда как учитывать их взаимное влияние друг на друга? Реальные искусственные системы, биологические системы, работают за счет взаимодействия частей, которые расположены близко.

Свойства структуры пространства показывают, что не оказывают влияния друг на друга величины (потоки) в замкнутых и разомкнутых путях (относящиеся к вращательному и поступательному движениям). Это происходит потому, что их матрицы преобразования путей при изменении структуры ортогональны, и произведения взаимных, недиагональных блоков равны нулю. Т.е. это отсутствие взаимодействия является свойством структуры, а не физического, материального взаимодействия.

Для описания системы материальных точек, которые взаимодействуют только между собой, недостаточно кинетической энергии. Оказывается , как замечает Ландау, что для описания взаимодействия точек в такой замкнутой системе нужно добавить функцию координат, зависящую от характера взаимодействия. Эту функцию, появление которой ниоткуда не следует, (т.е. она является понятием синтетическим, в смысле Канта ), называют потенциальной энергией системы U . Взаимодействие должно распространяться мгновенно, иначе его скорость распространения была бы различной для разных систем отсчета, а это противоречит принципу относительности. Собственные свойства пространства и времени, а также потенциальная энергия, дают вид функции Лагранжа.

L = V^- U (n ,r₂ ,^) = T-U , (6) где через U обозначена потенциальная энергия, зависящая от радиус-векторов r a . Таким образом, состояние системы определяется балансом между энергией движения (кинетической) T и энергией положения точек системы (потенциальной) U . По сути, эта функция есть совокупность видов энергии, которыми обладает данное тело. Подставляя в уравнения движения (2) системы материальных точек функцию Лагранжа из (6), получим известные уравнения второго закона Ньютона.

ma

dVa dt

3U „ dra - c

Вектор в правой части называется силой F, действующей на точку a. Размерность силы определяется массой, умноженной на ускорение, т.е. [F] = L4 T-4 в терминах LT- системы.

Функция Лагранжа равна разности суммы кинетических энергий частей и суммы потенциальной энергии частей. Энергия замкнутой системы равна сумме всех кинетических энергий частей и их потенциальных энергий. Кинетическая энергия определяется скоростями движения частей системы, а потенциальная энергия определяется координатами положения частей системы.

Отсюда следует изотропия времени, поскольку вид уравнений движения при изменении знака времени не меняется, т.е. все движения в механике обратимы.

Перемещение и вращение

Движения точки в пространстве бывают поступательные и вращательные. «Скорость любой точки (относительно неподвижной системы координат) может быть выражена через поступательную скорость тела и угловую скорость его вращения» [2, с. 124]. Это предполагает, что поступательное движение происходит по прямой линии, иначе в нем окажется составляющая вращательного движения.

Не существует других видов движений, кроме поступательных и вращательных движений, с помощью которых можно представить любое движение. Движения вращения и переноса не зависят друг от друга, но вместе с тем дополняют друг друга. Это два различных качества движения, которые обеспечивают полное описание движения.

Аналогично происходит движение материальных тел в пространстве. Теорема Эйлера в механике утверждает, что всякое движение тела можно представить как комбинацию поступательного движения и вращательного движения. «Всякое мгновенное движение твердого тела можно представить как результат сложения мгновенного поступательного движения со скоростью произвольно выбранной точки тела и мгновенного вращательного движения вокруг мгновенной оси вращения, проходящей через эту точку» [9, с. 184].

Движение тел по замкнутым и разомкнутым путям представляет собой потоки материи. Замкнутым и открытым потокам материи соответствуют замкнутые и открытые системы. Такие системы или взаимодействуют, или не взаимодействуют с телами в окружающем пространстве. Те и другие системы существуют во времени.

Элементы пространства и времени, точки и направления, равноправны и одинаковы. Существует непрерывность и всюду плотность (полное заполнение). Однако поступательное и вращательное движения неодинаковы, им соответствуют открытые и замкнутые пути в пространстве, которые связывает понятие двойственности.

Законы сохранения

При движении тел меняются значения их координат и скоростей. Некоторые величины, функции от координат и скоростей, при движении сохраняют постоянные значения, зависящие только от начальных условий. Эти функции называют интегралами движения. Поскольку уравнения движения замкнутой системы не содержат времени явно, то начало отсчета времени можно выбрать произвольно, и через эту постоянную выразить остальные. Поэтому для замкнутой системы с р степенями свободы число этих интегралов равно 2р – 1 [2, с. 23]. Несколько интегралов движения связаны с однородностью и изотропией пространства и времени, их и называют законами сохранения.

Таким образом, число интегралов движения зависит от числа степеней свободы, т.е. от сложности системы, числа ее элементов. Это представляется странным, поскольку законы сохранения связаны со свойствами пространства и времени, а не со свойствами конкретных систем, с их степенями свободы, расположенных в пространстве и двигающихся во времени. Если так рассуждать, то чем больше частиц и степеней свободы, тем больше есть интегралов движения, которые можно трактовать как законы сохранения.

Уравнения движения замкнутой системы позволяют вывести законы сохранения энергии, импульса и момента импульса с помощью свойств однородности и изотропии пространства и времени.

Симметрия и инвариантность

Известная теорема Э. Нетер доказывает, что каждой непрерывной симметрии пространства и времени соответствует некоторый закон сохранения. Эта теорема связывает симметрии (однородность и изотропию) пространства и времени с законами сохранения энергии, импульса и момента импульса, что позволяет проводить анализ физической системы на основе присущих ей свойств симметрии. Симметрия здесь рассматривается в широком смысле слова, как инвариантность (неизменность) структуры, формы объекта относительно его преобразования. В силу этого симметрия связывается с сохранением величин, характеризующих объект, например, энергии, импульса и т.д.

Вместе с тем симметрия, переводимая с греческого языка как «соразмерность», определяется как равномерное, сходное расположение частей геометрической фигуры, элементов формы предмета. Это свойство одинаковости относительно чего-либо – точки, оси, поверхности. Таким образом, симметрия предполагает удвоение понятий – два объекта расположены одинаково относительно некоторого центра.

При выводе законов сохранения из уравнений Лагранжа требуется не симметрия, а независимость функции Лагранжа от сдвигов в пространстве и во времени, или поворотов в пространстве. Эту независимость обеспечивают однородность и изотропия, т.е. одинаковость точек и направлений. Точки и направления не симметричны относительно какого-то центра, а просто одинаковы, так что нельзя выделить особенную точку, или особенное направление.

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

том 15 № 1 (42), 2019, ст. 1

При выводе законов сохранения из уравнений движения Ландау не упоминает о симметрии. Симметрия связана с инвариантностью структуры, формы объекта относительно его преобразования, а физики не рассматривают законы связей между элементами, законы структуры. Даже законы Кирхгофа часто называют «правила Кирхгофа», хотя это законы структуры связей.

В «Механике» Ландау и Лифшица нет ссылок на теорему Нетер. Они получают законы сохранения из принципа наименьшего действия, дающего уравнения движения, с использованием однородности и изотропии пространства (законы сохранения импульса и момента импульса), а однородность времени дает закон сохранения энергии. Изотропия времени также имеет место, но здесь не используется.

Закон сохранения энергии

Этот закон получается из уравнений движения в предположении однородности времени. Однородность времени означает, что функция Лагранжа замкнутой системы не зависит явно от времени, что предполагается и при выводе уравнений движения. Поэтому производная от функции Лагранжа по времени получается как дифференцирование сложной функции, куда входят производные по координатам и по скоростям, а частная производная по времени равна нулю.

dL =∑ ,^9L + ∑ .Эк⁹! dt dqi ^■^       £

„                                      dL                                   , . d 8L

Здесь заменяем производные   по уравнению Лагранжа (2) на      и получаем:

dL            dL ,                      d          ,

dt =∑i vi av. + ∑ldVi dt = ∑ i dt ( dv; Vi )

или, перенося все в левую часть, приводим производную по времени к нулю:

^ (∑ i V^ -L)=0

dt \ 1 1 dv; 7

откуда получаем, что величина в скобках, которая называется энергией, и обозначается E , не меняется при движении замкнутой системы, т.е.

E = ∑^iVi^- L =                                                  (10)

Энергия системы частиц аддитивна, т.е. равна сумме энергии отдельных частиц при отсутствии взаимодействия между ними, поскольку аддитивна функция Лагранжа. Для замкнутой системы функция Лагранжа имеет вид разности кинетической энергии и потенциальной энергии, см. (6).

L=(q, ̇)- и(q).

Подставляя это выражение в (10), и выполняя преобразования [2, с. 25], получим, что

E = T(q,q) + U(q).                                                            (11)

Таким образом, энергия при движении замкнутой системы постоянна. Она равна сумме кинетической энергии, зависящей от скоростей, и потенциальной энергии, зависящей от координат. Уменьшение энергии одного вида влечет за собой увеличение энергии другого вида, и наоборот. Простым примером является движение маятника.

Закон сохранения импульса

Поскольку пространство однородно, то механические свойства замкнутой системы не меняются при параллельном переносе в пространстве. Пусть все точки системы смещаются на бесконечно малый отрезок , при неизменных скоростях частиц системы, при этом их радиус-векторы меняются с r на r’ = r + . Тогда изменение функции Лагранжа имеет вид.

6L = 2^8^ = к^Л дГ[ 1          drt где берется сумма по всем элементам (материальным точкам) системы. Поскольку приращение k произвольно, а вариация должна равняться нулю, то и производная функции Лагранжа по радиус-вектору r должна равняться нулю.

Подставляя это соотношение в уравнения Лагранжа (2), видим, что второй член равен нулю и тогда получим:

y.2£ = dt dvi

Таким образом, получаем, что дифференцируемая по времени функция, которую называют импульс, обозначая P , остается постоянной при движении замкнутой системы:

2 1^ = 2 im_t ^. =S im_t v_z = P_t = const (12)

Это значит, что производная функция Лагранжа по скорости, импульс P , не меняется при движении замкнутой системы. Сохраняется векторная величина импульса; по каждой оси координат проекция величины импульса остается постоянной, т.е. имеется три закона сохранения импульса. Импульс системы частиц равен сумме импульсов отдельных частиц, не зависимо от взаимодействия между ними.

Производная функции Лагранжа по радиус-вектору r есть сила F – см. (7), действующая на частицу. Таким образом, из однородности пространства следует равенство нулю суммы сил, действующих на все частицы замкнутой системы. Для системы, состоящей из двух материальных точек, это означает, что они действуют друг на друга с равными и противоположными по направлению силами, что соответствует закону равенства действия и противодействия. Этот закон сохранения связан с переносом, поступательным движением.

Закон сохранения момента импульса

Поскольку пространство изотропно, то механические свойства замкнутой системы не меняются при вращении, повороте системы как целого в пространстве. Рассмотрим бесконечно малый поворот системы и постоянство функции Лагранжа при этом.

Абсолютная величина вектора бесконечно малого поворота 5р равна углу поворота Р<р, а направление совпадает с осью поворота. Направление поворота соответствует правилу винта относительно направления 5р.

Приращение радиус-вектора r от начала координат на оси вращения до одной из точек системы связано с вектором поворота и углом 6 отклонения радиус-вектора от оси вращения. Линейное перемещение конца радиус-вектора определяется его величиной, углом поворота и углом отклонения от оси соотношением [2, с. 29]:

|5r| = г sin 6 Р(р                                                                     (13)

Направление вектора приращения перпендикулярно к плоскости, проходящей через радиус-вектор r и вектор поворота 5 р. Таким образом, приращение радиус-вектора равно их векторному произведению.

5r = [5р г]

При повороте системы направление не только радиус-вектора, но и скоростей всех частиц меняется по одинаковому закону. По этой причине приращение скорости относительно неподвижной системы координат так же имеет вид векторного произведения.

5v = [5р vj                                                                    (14)

При повороте функция Лагранжа не меняется в силу изотропии пространства, поэтому ее вариация по радиус-вектору и скоростям равна нулю:

6L = (^Sr+Z ^8^ =0                            (15)

где берется сумма по всем элементам (материальным точкам) системы. Производная функции Лагранжа справа есть импульс, а слева – сила, или производная импульса по времени. Подставив (13) и (14) в (15), а также заменяя производную функции Лагранжа по скорости на импульс, а производную функции Лагранжа по координатам на силу, получим:

Z i (pЛ<^р r^] + p_t^[5р vj) =o                                                (16)

Производя в этом выражении циклическую перестановку в скалярном и векторном произведениях по правилам векторного исчисления, получим:

5P Z i ([r_fp₍| + |v , p i ^j) = 5p ^Zi^ p t ^j= 0                                     (17)

Поскольку приращение вектора поворота произвольно, то векторная величина под знаком суммы остается постоянной при движении замкнутой системы. Эта величина называется моментом импульса, или моментом системы, и обозначается M .

Zifa P t ] = c oss t = M (18)

Момент импульса системы частиц равен сумме моментов импульсов отдельных частиц, не зависимо от взаимодействия между ними. Момент импульса сохраняется по каждому из трех измерений, как и величина импульса.

Этот закон сохранения связан с вращательным движением.

Таким образом, получены законы сохранения при движении замкнутой системы: энергии и по три компоненты векторов импульса и момента импульса. Для этого использованы принцип наименьшего действия, однородность и изотропия пространства и времени, а также законы вариационного и векторного исчислений.

Постулаты механики

Законы сохранения выводятся из уравнений движения механических систем. При этом делается ряд рассмотренных выше допущений, которые имеют характер аксиом. Они ниоткуда не вытекают, опираются на опыт, либо вводятся по причине «оказывается, что…».

Как показывает опыт , состояние системы полностью определяет задание всех координат и скоростей (по ним можно найти значения ускорений).

На основе опыта принимается принцип наименьшего действия, который утверждает, что система двигается оптимальным образом. За время движения по реальному пути величина действия принимает наименьшее значение. Действие представляет собой интеграл от функции положения, скоростей и времени.

При выводе уравнений движения берут вариацию – разность между функцией, которая имеет наименьшее действие, и функцией, которая от нее отклоняется. Разность раскладывают по степеням и берут только члены вариации первого порядка (приравнивая их к нулю), а членами более высокого порядка пренебрегают. В теории катастроф показано, что малые отклонения в функции могут приводить к большим изменениям.

По отношению к произвольной системе отсчета пространство неоднородно и не изотропно. То есть, если какое-либо тело не взаимодействует с другими телами, то, тем не менее, его различные положения и его ориентации в пространстве в механическом отношении не эквивалентны. Однако собственные свойства пространства, однородность и изотропия, не могут зависеть от систем отсчета, которые вводит наблюдатель.

• •    Оказывается , что всегда можно найти такую систему отсчета, по отношению к которой пространство является однородным и изотропным, время – однородным. Эта система называется инерциальной .

• •    Опыт показывает , что не только законы свободного движения будут одинаковы в инерциальных системах отсчета, но что они будут и во всех других механических отношениях полностью эквивалентными.

• •    Оказывается , что взаимодействие между материальными точками может быть описано прибавлением к функции Лагранжа невзаимодействующих точек определенной (зависящей от характера взаимодействия) функции координат. Так вводят потенциальную энергию. Однако до этого принимается, что функция Лагранжа не зависит от радиус-вектора, т.е. от координат.

Экскурс в теоретическую физику интересен тем, что законы сохранения связывают со свойствами пространства через уравнения движения достаточно произвольного вида. Эти уравнения получены из формальной задачи об определении экстремума интеграла от положения, скорости и времени, которая решается в рамках вариационного исчисления.

Инвариант двойственности при изменении структуры пространства

Законы сохранения в механике при движении замкнутых систем основаны на свойствах одинаковости точек и направлений (однородности и изотропии) пространства и времени. Все движения состоят из поступательного движения (параллельного переноса) и вращательного движения (вокруг оси). Перенос и вращение неодинаковы. Они независимы и составляют «базис» движений в пространстве. Любое движение раскладывается на поступательное и вращательное движение. Закон сохранения импульса связан с переносом, закон сохранения момента импульса связан с вращением.

Перенос происходит вдоль разомкнутых путей, а вращение происходит вдоль замкнутых путей. Есть только замкнутые и разомкнутые пути, определяющие свойства структуры пространства.

При соединении системы из элементов в сеть, изменении структуры, меняется число базисных замкнутых и разомкнутых путей. В двойственных сетях каждому замкнутому пути соответствует разомкнутый путь, и наоборот. В двух двойственных сетях сумма базисных замкнутых и разомкнутых путей постоянна. Инвариант двойственности есть постоянство суммы метрических тензоров двух двойственных сетей при любой структуре соединения элементов. В двойственных электрических цепях постоянна сумма рассеиваемых мощностей при изменении структуры. Иными словами в двойственных цепях при изменении структуры остается постоянным поток энергии. Две двойственные цепи взаимно изменяют структуру, чтобы сохранялась двойственность, но остаются замкнутой системой, которая не взаимодействует с окружающей средой. Постоянство мощности в двойственных цепях при изменении структуры есть закон сохранения потока энергии.

Подпространства путей меняют размерности при изменении структуры

Части пространства, вдоль которых происходит движение, представляют собой элементы системы. Сеть – это совокупность элементов системы. Соединения элементов границами – это структура сети. При изменении структуры связей элементов системы сливаются или разделяются границы; происходит замыкание и размыкание путей. При размыкании контура возникает разомкнутый путь, а замкнутый путь исчезает. При соединении начала с концом разомкнутого пути возникает замкнутый путь, а разомкнутый путь исчезает. Это приводит к изменению размерностей их подпространств, которые составляют ортогональные и взаимно дополняющие друг друга подпространства сети, системы. Соответственно, меняются метрические тензоры этих подпространств.

Таким образом, при изменении структуры меняются размерности подпространств замкнутых и разомкнутых путей, но сумма их размерностей постоянна, и равна числу элементов системы. Также меняются и размерности подпространства вращений и переносов. Наличие структуры в обычном пространстве проявляется в разделении на ортогональные подпространства замкнутых и разомкнутых путей. Вместе с тем это свойство уже заложено существованием различий вращений и переносов.

Изменение размерностей подпространств замкнутых и разомкнутых путей вносит асимметрию в преобразование структуры. Сохранение симметрии при изменении путей, постоянство суммы размерностей пространств замкнутых и разомкнутых путей, обеспечивает двойственное пространство. В двойственном пространстве существует двойственная сеть, в которой каждому замкнутому пути сети соответствует разомкнутый путь, и наоборот. При уменьшении замкнутых путей в одной сети возрастает их число в двойственной сети, так что число базисных замкнутых путей в двух сетях постоянно. При уменьшении разомкнутых путей в одной сети возрастает их число в двойственной сети, так что число базисных разомкнутых путей в двух сетях постоянно.

Кроме того, оказывается, что существует постоянство суммы метрических тензоров двух сетей с двойственной структурой при изменении соединения ветвей, что является инвариантом пространства. Этому свойству, которое можно рассматривать как симметрию двух двойственных пространств, соответствует закон сохранения потока энергии.

Структура и тензорный анализ сетей Крона

Исследования структуры пространства развивались со времен Кирхгофа. Он опубликовал доказательство существования решения задачи сети с «чистыми» сопротивлениями (без индуктивностей) в 1845 и 1847 годах, найдя соотношение инцидентности для одномерного комплекса (законы Кирхгофа). В 1865 г. Максвелл заметил, что Кирхгоф не включил понятие потенциала, и создал два метода решения задачи сети, которые теперь называют контурным и узловым методом [12]. В 1923 году Г. Вейль доказал результат Кирхгофа методами топологии. Он рассматривал ток и напряжение как контравариантный и ковариантный векторы.

В 30-тых годах Г. Крон разработал тензорный анализ сетей, как неподвижных электрических сетей, так и вращающихся электрических машин. В 40-50-тых годах Крон создал ряд моделей в виде эквивалентных электрических цепей для различных физических систем, включая уравнения Максвелла, Шредингера, Навье-Стокса, и технических систем, например, ядерного реактора, энергетических систем, строительных конструкций, лопаток турбин, транспортной задачи. Затем последовали развитие теории и новые приложения.

Идея Крона состояла в использовании тензорного метода для расчета сетей, электрических машин, других технических систем. Система рассматривается как тензор, а различные соединения ее элементов – как проекции в разные системы координат. Можно произвести расчет одного варианта структуры системы, а расчеты других вариантов получать как преобразование координат. Например, рассчитать систему, состоящую из отдельных элементов, а затем перейти к соединенной системе с помощью матрицы преобразования координат-путей при изменении структуры.

Любой процесс состоит из воздействия, отклика и метрики, которая устанавливает пропорции между воздействием и откликом, характеризуя свойства материи данной системы. При изменении системы координат преобразование величины бывает ковариантным или контравариантным. Т.е. величина преобразуется с помощью той же матрицы, что и базис путей, или с помощью обратной матрицы, т.е. противоположно базису.

Крон рассматривал электрическую цепь из ветвей как тензор, а разные структуры соединения ветвей, как его проекции в разные системы координат. Переход от одной сети к другой можно рассматривать как преобразование координат. Для этого при соединении отдельных ветвей в связанную сеть величины сети должны иметь тензорные (линейные) формулы преобразования. Токи в простейшей контурной сети из замкнутых отдельных ветвей, представленные вектором i, и токи в базисных контурах связанной сети, представленные вектором i' связывает матрица преобразования C (индексы везде опускаем).

i = C i'                                                                                     (19)

Если в связанной сети есть только контуры, то матрица C квадратная, она имеет обратную матрицу, т.е. можно сделать и обратное преобразование.

Для получения тензорной формулы преобразования вектора напряжения необходима такая величина, которая одинакова для обеих сетей. Полная мгновенная мощность P, потребляемая всей системой, сетью, равна сумме произведений тока и напряжения по всем ветвям. Крон постулировал , что мощность P в сети из отдельных ветвей не меняется при соединении ветвей, т.е. равна мощности P' сети из соединенных ветвей, [5, с. 140], P = P^ .

Контурная сеть. Простейшая сеть состоит из замкнутых ветвей с источниками напряжения e . Мощность в простейшей сети есть сумма произведений напряжения и тока по каждой ветви: P = e i , а мощность в связанной сети, аналогично, P' = e' i' Приравнивая, согласно постулату Крона, выражения для мощностей, и подставляя выражение для вектора тока, получим как скалярные произведения векторов:

e i = e' i' = e C i' , откуда e' = e C= C_t e , т.е.:

e = C_t "1 e' или e' = C_t e.                                                               (20)

По сути это ключевой момент тензорного анализа сетей Крона, который дает законы преобразования величин в сети при изменении структуры связей. Из формул преобразования тока и напряжения можно получить формулу преобразования метрического тензора сети – комплексного сопротивления ветвей Z (импеданса). Поведение цепи описывает закон Ома: в простейшей сети (несоединенные ветви) e = Z i , а в связанной сети e' = Z' i'. Подставляя в первое уравнение выражения (19) и (20) для тока и напряжения, получим:

Ct"¹ e' = Z C i' , откуда e' = Ct Z C i'

Сравнив это со вторым уравнением, видим, что выражения перед i' должны быть одинаковыми, откуда получаем формулу преобразования матрицы импеданса для базисных замкнутых путей связанной сети:

Z' = C t Z C                                                                  (21)

Отсюда, зная решение простейшей сети, с помощью матрицы преобразования получим решение связанной сети – для заданных источников напряжения и импедансов ветвей. В самом деле, получим отклики – токи – из уравнения закона Ома для связанной сети, и подставим туда формулы преобразования импеданса и напряжения:

e' = Z' i', откуда i' = (Z') "1 e' = (C t Z C)^-1 C t e.                                        (22)

Это выражение для токов в базисных контурах связанной сети. Для перехода к токам в отдельных ветвях i с , которые являются измеримыми величинами, надо использовать выражение (19), тогда получим:

i с = C i` = C (C t Z C) ^-1 C t e = Y с e. (23)

Через Y с обозначена матрица, которую назовем «матрица решения». Она позволяет рассчитать отклики-токи в ветвях связанной сети по заданным источникам напряжения (ЭДС) в отдельных ветвях. Эта матрица представляет метрический тензор ветвей связанной сети для подпространства замкнутых путей.

Если при соединении ветвей часть контуров оказалась разомкнута, то матрица преобразования будет не квадратная, а прямоугольная. В полученных формулах расчета сети обратной матрицы преобразования нет. Но она возникает при выводе формулы преобразования напряжения (20), тогда это преобразование недопустимо , поскольку прямоугольная матрица не может быть обращена. Мощность при уменьшении числа базисных контуров также меняется, она не увеличивается. Это доказано теоремой Волавера в теории графов. Таким образом, инвариант мощности в общем виде не выполняется .

Узловая сеть. Простейшая сеть состоит из разомкнутых ветвей с источниками тока I , когда ток поступает в сеть в одном узле, а покидает в другом узле. Здесь переменными являются не контуры, а пары узлов, разности потенциалов на которых определяют напряжение на ветвях. Пары узлов, по сути, представляют разомкнутые пути, соединяющие ветвями два узла. В предисловии к изданию 1965 года Крон признал, что понятие открытого пути лучше, чем «пара узлов» [5, с. 26]. Однако он не стал отходить от электрической цепи с токами и напряжениями, и переходить к чистой структуре. Это направление развил его последователь Х. Хэпп [13], который также не решил проблему инварианта мощности.

Формулы расчета узловой сети двойственны к формулам расчета контурной сети с заменой источников напряжения e на источники тока I , токов отклика в ветвях i с на напряжения отклика на ветвях E с , сопротивления Z на проводимость Y = Z^-1 и матрицы преобразования C на ортогональную А = C^-1 t . Для уравнения простейшей сети I = Y E получим отклики в связанной сети аналогично (23) с двойственными заменами:

E с = А (А t Y А) ^-1 А t I = Z с I (24)

Через Z с обозначена матрица решения, которая позволяет рассчитать отклики-напряжения на ветвях связанной сети по заданным источникам тока на отдельных ветвях. Эта матрица представляет метрический тензор сети в подпространстве разомкнутых путей.

Формула (23) соответствует преобразованию простейшей контурной сети в связанную сеть с таким же количеством контуров. Формула (24) соответствует преобразованию простейшей сети из разомкнутых ветвей в связанную сеть с таким же количеством разомкнутых путей (пар узлов). Это частные случаи преобразования структуры.

В общем случае при соединении отдельных ветвей в связанную сеть происходят изменения структуры, которые состоят в том, при слиянии или разделении границ ветвей часть контуров размыкается, а часть открытых путей замыкается. Тогда меньшее число базисных контуров в связанной сети выражается через большее число контуров в простейшей сети. Матрица преобразования контуров C становится прямоугольной. Подматрицу, которая выражает преобразование контуров, обозначают ^mC . Ее дополняет подматрица, выражающая преобразование разомкнутых путей, обозначаемая ^jC . В общем случае в (23) матрицу C заменяют на подматрицу ^mC для расчета контурной сети.

Аналогичная ситуация возникает при соединении разомкнутых ветвей в связанную сеть, когда часть открытых путей замыкается, и становится контурами. Тогда меньшее число базисных разомкнутых путей в связанной сети выражается через большее число разомкнутых путей в простейшей сети прямоугольной подматрицей ^jА . Ее дополняет подматрица преобразования контуров, обозначаемая ^mА . В общем случае в (24) должна быть подматрица ^jА, для расчета узловой сети.

Прямоугольные матрицы преобразования не образуют группу , поскольку нельзя сделать обратное преобразование. В геометрии преобразования координат образуют группу, что отмечал О. Веблен. Постулат об инварианте мощности не выполняется . Однако метод, основанный на неправильном постулате, и матрицах преобразования, которые не образуют группу, дает правильные результаты расчета сетей и сетевых моделей сложных систем. Противоречия тензорного анализа сетей Крона сделали его объектом критики на протяжении десятков лет [7].

Крон пытался использовать ортогональные сети, в которых в качестве переменных используются и контуры и пары узлов. Тогда матрица преобразования квадратная и мощность сохраняется. Однако получаемые токи и напряжения на ветвях не удовлетворяют законам Кирхгофа, т.е. не соответствуют решению задачи сети. Дело в том, что включение пар узлов в подматрицу ^mС превращает их в контуры, и получается чисто контурная сеть.

Получилось диалектическое противоречие: посылки неправильные – результат правильный; посылки правильные – результат неправильный. Это противоречие и нашло свое разрешение через двойственные сети. В каком-то смысле двойственные сети соответствуют понятию ортогональной сети, но контуры в сети дополняются не парами узлов (разомкнутыми путями) в той же сети, а соответствующими этим парам узлов контурами в двойственной сети.

Оказалось, что при изменениях структуры постоянна сумма метрических тензоров, матриц решения, в двух двойственных сетях, и эта сумма равна метрическому тензору в простейшей сети. Такая сумма метрических тензоров, при единичных весах ветвей, выражает свойство двойственности структуры пространства, и имеет вид:

^mC t (^mC ^mC t )^{–1 m}C + ^m C t (^m C ^m C t )^{–1 m} C = I                                            (25)

Двойственность является свойством пространства, таким же, как однородность и изотропия. Это дает теоретическую основу тензорного метода в теории систем.

Следствием этого является постоянство суммы рассеиваемых мощностей в двух двойственных сетях при любой структуре и ее изменениях, и она равна мощности в простейшей сети.

Структура пространства

Структура есть способ, схема соединения частей, которые составляют систему. Части, элементы, соединяются и разделяются своими границами. Предполагается, что внутренность элемента между границами не изменяется при соединениях и разделениях.

При переходе к структуре пространства изменяется смысл понятия непрерывности. При изменении структуры системы соединение и разделение частей происходит скачком. Пространство структуры по своей сути является дискретным. Нет плавного, непрерывного перехода с бесконечно малыми изменениями от состояния «соединение есть» к состоянию «соединения нет». Рассмотрим свойства структуры и ее изменений.

Пространство структуры непрерывно вдоль выделенных направлений – ветвей, но вне ветвей пространство не рассматривается. Нет бесконечно малых изменений, с помощью которых получены законы сохранения энергии, импульса и момента импульса. Ветвь представляет собой отрезок линии, имеющей направление, границами которой являются точки (узлы). Ветвь бывает замкнутая (ее границы соединены) или разомкнутая.

В общем виде «ветвь» – это элемент сети, системы, часть пространства. Например, отрезок, грань, объем. «Ветвь» имеет свои границы, соответственно, точки, отрезки, грани.

Путь – это абстрактная линия, проходящая вдоль ветви (или нескольких ветвей), направление совпадает с направлением ветви, или противоположно ей. Путь есть способ арифметизации структуры пространства. Пути вдоль выбранных ветвей являются координатами в структуре пространства.

Совокупность ветвей составляет сеть, ветви могут соединяться своими границами, узлами. В сети двойственными являются замкнутые и разомкнутые пути, токи и напряжения, воздействия и отклики, внешние воздействия и внутренние воздействия.

У путей есть границы – начало и конец. Начало и окончание разомкнутого пути не совпадают, находятся в двух разных точках, узлах. Начало и окончание замкнутого пути совпадают, находятся в одной точке. Ветви, изменяют связи, соединяя свои границы, или разделяя. В этом состоит изменение связей, преобразование структуры. Замкнутые пути могут размыкаться, а разомкнутые пути могут замыкаться.

Асимметрия путей состоит в том, что замкнутые пути можно выразить через замкнутые и разомкнутые пути, а разомкнутые пути нельзя выразить через замкнутые пути. Это объясняется тем, что замыкание пути охватывает новое измерение пространства. Например, замыкание линии в кольцо охватывает кусок 2-мерной поверхности, а замкнутый 2-путь получается при замыкании граней в 3-мерный объем и т.д. Так переход от поступательного движения по разомкнутому пути к вращательному движению по замкнутому пути порождает, вводит новое измерение пространства.

Каждая ветвь определяет размерность в пространстве структуры. Размерность пространства структуры равна числу ветвей, а пути задают координаты в структуре. Замкнутые пути образуют одно подпространство, а разомкнутые пути образуют другое подпространство. Вместе эти два подпространства образуют полное пространство структуры. В каждом из них независимые пути образуют базис.

Базис замкнутых путей m должен охватить все ветви сети. Базис разомкнутых путей j должен охватить все узлы сети. Их размерности определяют соотношения [1, 3].

j = J – s , (26)

n = m + j. (27) где n – количество ветвей в сети, J – количество узлов, s количество – подсетей, m – независимых замкнутых путей, j – независимых разомкнутых путей. Числа m и j определяют размерность каждого подпространства. Сумма независимых замкнутых и разомкнутых путей постоянна, и равна числу ветвей.

Для перехода от одного соединения элементов к другому, пути в новой системе выражают через пути в старой системе, комбинируя составляющие их ветви с учетом ориентации. Коэффициенты выражения путей составляют матрицу преобразования путей С , например, перехода от свободных ветвей к связанной сети. Это описание изменения структуры соответствует преобразованию координат в обычном пространстве.

Матрица преобразования путей С соответствует транспонированной матрице преобразования токов Крона, которая также обозначается С .

Простейшая сеть из несоединенных ветвей соответствует системе из частей, которые не взаимодействуют. Уравнения движения (например, закон Ома) описывают процессы в каждой ветви отдельно, и независимо от других ветвей. При соединении ветвей возникают связи, которые изменяют пути, уменьшая число степеней свободы, размерность их пространства. Наложение связей при соединении отдельных контуров уменьшает (не увеличивает) число базисных контуров в сети. Или наложение связей при соединении отдельных разомкнутых путей уменьшает (не увеличивает) число базисных разомкнутых путей в связанной сети.

В теории резистивных цепей это формулируется как свойство неусиления токов и напряжений на ветвях по сравнению с токами и напряжениями на источниках, т.е. физических величин. Но доказывается это свойство леммой о раскраске графов с применением законов Кирхгофа к циклам и разрезам. Т.е. как приложение теории графов к электрическим цепям.

Двойственные сети

При изменении структуры замкнутые пути размыкаются, а разомкнутые пути замыкаются. При размыкании контуров растет число независимых разомкнутых путей и размерность их подпространства, а размерность подпространства замкнутых путей уменьшается. При замыкании разомкнутых путей их подпространство уменьшается, а размерность подпространства замкнутых путей возрастает.

Уменьшение числа базисных путей при соединении ветвей в сеть приводит к уменьшению мощности. Постоянство мощности обеспечивает двойственная сеть, в которой происходят обратные изменения структуры. По своей сути объект «Сеть» состоит из двух частей, двух сетей с двойственной структурой. Замкнутому пути в одной сети соответствует разомкнутый путь в двойственной сети, а разомкнутому пути в сети соответствует замкнутый путь в двойственной сети. В теории графов двойственность определяется аналогично.

Элемент сети – двойственная ветвь, состоящая из двух частей: замкнутой и открытой. Координаты ветви – замкнутый путь в замкнутой части и открытый путь в открытой части. Ветви могут соединяться своими границами, образуя две сети. При изменении структуры сохраняются свойства двойственности. Две двойственные сети структурно дополняют друг друга до полного пространства.

Преобразования структуры в двойственных сетях:

• • разрыванию в сети соответствует соединение в двойственной сети

соединению в сети соответствует разрывание в двойственной сети.

сумма замкнутых путей и сумма разомкнутых путей остаются постоянными.

Двойственная сеть дополняет исходную сеть до полной сети. Обозначим величины в двойственной сети подчеркиванием, тогда соотношения (26) и (27) будут иметь вид.

j = m = J – s ,                                                                    (28)

n = m + j , откуда m = n – j = n – m = j.                                         (29)

Таким образом, размерность подпространства замкнутых путей в сети равна размерности подпространства разомкнутых путей в двойственной сети, и наоборот.

Инварианты изменения структуры двух двойственных сетей

Существуют величины, которые остаются постоянными при любой структуре соединения ветвей двойственных сетей:

• 1.    количество ветвей в каждой сети одинаково и постоянно n = n = const ;

• 2.    сумма независимых контуров в двух сетях постоянна: m + m = n = const ;

• 3.    сумма независимых разомкнутых путей в двух сетях постоянна: j + j = n = const ;

• 4.    сумма модулей степеней узлов в двух сетях , определяющая ориентацию ветвей относительно узлов, есть величина постоянная: k + k = k 0 = n + n = 2n = const .

Первый инвариант показывает, что размерность полного пространства сети постоянна, т.е. число элементов-ветвей не меняется. Меняется размерность подпространств замкнутых и разомкнутых путей в каждой сети при разделении или соединении узлов. Инварианты второй и третий показывают, что в двух двойственных сетях сумма размерностей подпространств, как замкнутых путей, так и разомкнутых путей, постоянна при любых изменениях структуры, хотя в каждой из сетей эти размерности меняются. Четвертый инвариант показывает, что сумма ориентации ветвей, входящих в узел в данной сети, и охватывающего контура в двойственной сети равны. Ветвь в двух сетях реализует обе ориентации.

Оказывается, что существует пятый инвариант, инвариант двойственности, который представлен в (25) для единичной метрики, т.е. когда веса ветвей равны единицам, Z = Y = 1 . Он выражен только через матрицы преобразования, представляя свойства самой структуры, без метрики, и физических величин. Если метрика не единичная, Z = Y^-1 то сумма метрических тензоров двойственных сетей постоянна и равна метрическому тензору свободных ветвей.

Для замкнутых путей с метрикой, весами ветвей, инвариант имеет вид:

Y = ^mC ( m C Z ^mC J^{1 m}C + Z ^mC_t (^mC Z ^mC t )^{1 m}C Z,

Для разомкнутых путей с метрикой, весами ветвей, инвариант имеет вид:

Y = ^jA_t (A ZA t )^{1 j}A + ZA_t (A Z A t )^{1 j}A Z                                    (31)

Нетрудно видеть, что слагаемые в формулах (25), (30) и (31) представляют собой полученные выше формулы решения, или метрические тензоры связанных контурных и узловых сетей.

Закон сохранения мощности (потока энергии)

Найденному инварианту двойственности соответствует постоянство суммы рассеиваемых мощностей двух электрических цепей с двойственной структурой при изменении соединений.

Отклики в ветвях связанной сети были получены в (23) для внутренних воздействий и замкнутых путей. Мощность в ветви равна произведению тока на напряжение. Для цепи из нескольких ветвей мощность запишем как скалярное произведение векторов тока и напряжения. По нижнему и верхнему индексу предполагается суммирование.

Мощность, рассеиваемая в простейшей цепи, ^mP 0 = e i равна мощности источников.

Мощность, рассеиваемая в контурах связанной цепи ^mP' = e_a Р' .

Мощность в отдельных ветвях связанной цепи ^mP c = i с e ^с = ^mP` .

Отклики в ветвях связанной сети были получены в (24) для внешних воздействий и разомкнутых путей. Для узловой сети, получим аналогично.

Мощность, рассеиваемая в простейшей цепи ^jP 0 = I 0 E 0 равна мощности источников.

Мощность, рассеиваемая в разомкнутых путях связанной цепи ^jP' = Г' Е_а

Мощность в отдельных ветвях связанной цепи ^jP c = E ^с I с = ^jP` .

Формулы расчета двойственных цепей аналогичны формулам для исходной цепи, но с двойственными заменами всех величин. Например, формула расчета токов в ветвях двойственной цепи по источникам ЭДС подобна (23).

i с = m C t ( m e Z m e t )i m e e^ = Y jA (A Y j A t ) ¹ A y e^                                (32)

Расчет напряжения в ветвях двойственной цепи по источникам тока подобен (24).

E сс = ^jA._t (A ZA t )" ^{1 j}A I = Z ^mC_t (^mC Z m C ) ^{-1 m}C ZI                                 (33)

Мощности получаются по матрицам решения контурных и узловых сетей, которые входят в инвариант двойственности.

Для замкнутых путей закон постоянства мощности, рассеиваемой в двух двойственных цепях при изменении структуры соединения ветвей, имеет вид.

^mP c + ^m P c = ^mP` + <sup>m</sup> P ` = ^mP 0 .                                                    (34)

Для разомкнутых путей закон постоянства мощности, рассеиваемой в двух двойственных цепях при изменении структуры соединения ветвей, имеет вид.

• ^jP c + ^j P c = ^jP` + <sup>j</sup> P ` = ^jP 0 .                                                             (35)

Первая формула утверждает, что суммарная мощность, рассеиваемая в двух двойственных цепях при возбуждении источниками ЭДС, постоянна и равна мощности источников, т.е. мощности, рассеиваемой в свободных ветвях. Вторая формула утверждает, что суммарная мощность, рассеиваемая в двух двойственных цепях при возбуждении источниками тока постоянна и равна мощности источников, т.е. мощности, рассеиваемой в свободных ветвях. Если заданы источники тока и напряжения одновременно, то получим общую формулу постоянства мощности при изменении структуры двойственных цепей.

• ^mP c + ^m P c + ^jP c + ^j P c = ^mP 0 + ^jP 0 = ^m P 0 + ^j P 0 ,                                         (36)

где мощности представлены в отдельных ветвях, т.е. через измеримые величины.

Представим мощности через матрицы решения, значения токов и напряжений в путях или ветвях, что по своей сути одно и то же, и определяется только выбором координат. Для замкнутых путей, источников ЭДС, постоянство мощности в двойственных цепях принимает следующий вид. В этих формулах опустим индексы путей, чтобы упростить выражения. Например, для замкнутых путей получим следующее

• ^mP 0 = ^mP c + ^m P c ,                                                                 (37)

где   mPo = e (Z)1 e mPc = e mCt (mC Z mC t)1 mC e mPc = e Z mCt (mC Z mCt)1 mC Z e= e YjAt (A YjA t)1 jA Y e

Подставим выражения компонент мощности в уравнение (37), получим:

e Ye = e mCt (mC Z mCt)1 mC e + e_ Z mC^ (mC Z mCt)1 mC Z e, т.е. постоянство суммы мощностей в замкнутых путях двух двойственных цепей при изменении структуры.

Для разомкнутых путей получается аналогичная двойственная формула постоянства суммы мощностей в цепях с двойственной структурой для любых способов соединения их ветвей.

Найденный инвариант, представленный в [7, 8], определяет свойство двойственности пространства, дополняющее свойства однородности и изотропии. Замкнутые и разомкнутые пути, которые служат маршрутами вращений и перемещений, образуют структуры, дополняющие друг друга в двойственных сетях. Этой двойственности соответствует закон сохранения мощности, или закон сохранения потока энергии.

Примеры преобразования структуры двойственных сетей

Пример двойственных сетей и матриц преобразования для одного из вариантов выбора путей представлен на рисунке 1.

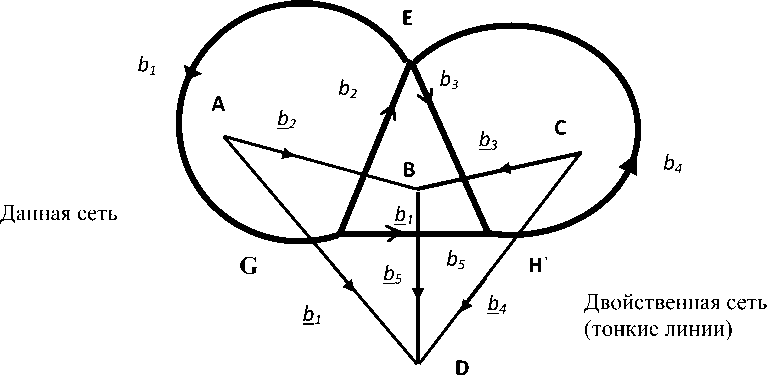
Рис. 1. Двойственные сети из 5 ветвей. Контуру в одной сети соответствует разомкнутый путь в другой сети, и наоборот

Этим сетям соответствуют матрицы преобразования путей старого базиса свободных, не соединенных ветвей в новый базис путей в связанных ветвях. Матрица преобразования C исходной сети (жирные линии) и матрица преобразования С = А= С¹₁ двойственной сети (тонкие линии). Величины двойственной сети обозначены подчеркиванием.

Р1 Р2 Рз Р4' Рз Р1 Р2 Рз Р.4 Рз Р1" 1 1 m Р1' 1 1 Р2" 1 1 -1 m Р2' -1 1 1 Рз" 1 1 m с;1 = Рз' 1 -1 1 1 С = Р4" 1 1 С = А = Р4' -1 1 -1 1 m Рз" 1 1 Рз' -1 1 1 m m  m  m  m Матрицы преобразования m     ill от базисов свободных ветвей к базисам 1     1 связанных ветвей, и наоборот имеют ' нулевой блок выражения разомкнутых путей через замкнутые пути. Буквы в строке под матрицами показывают, что в простейшей сети отдельные ветви в данной сети были все замкнуты, а в двойственной сети были все разомкнуты.

Двойственные сети, таким образом, связывают метрику и структуру, что позволяет применять сетевые модели для расчета и анализа систем с переменной структурой. Можно находить скрытые структурные свойства систем, производить расчет изменения процессов при изменении структуры, использовать результаты одной структуры для других структур, как преобразование координат.

Расчет метрических тензоров двойственных сетей при изменении структуры

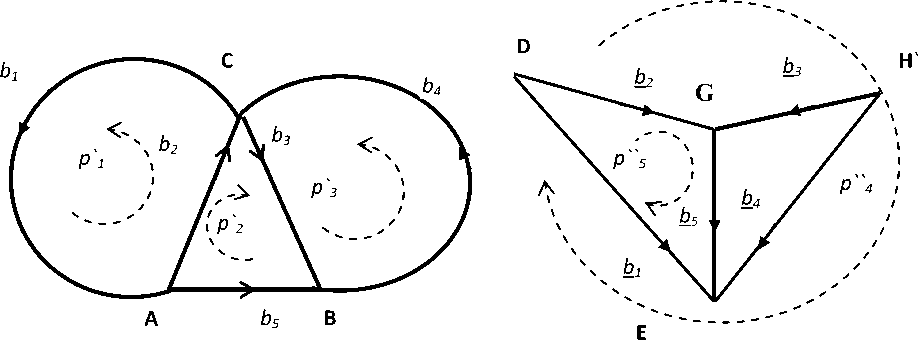
Двойственные сети из пяти ветвей до изменения структуры представлены на рисунке 2.

Двойственная сеть

Данная сеть

Рис. 2. Двойственные сети из 5 ветвей

Этим сетям соответствуют матрицы преобразования путей базиса не соединенных ветвей в базис путей в связанных ветвях. Матрица преобразования C исходной сети (слева) и матрица преобразования С = А = С -t двойственной сети (справа)

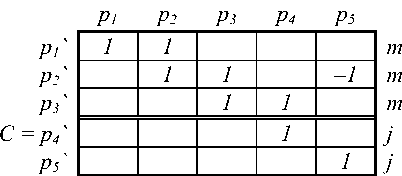
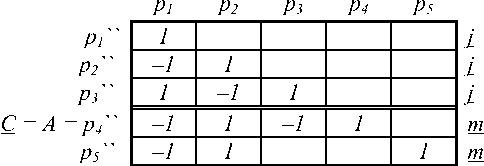
Матрицы преобразования от базисов свободных ветвей к базисам связанных ветвей, и наоборот имеют нулевой блок выражения разомкнутых путей через замкнутые пути.

Метрический тензор, как мера в пространстве, связывающая ковариантные и контравариантные компоненты вектора, воздействия и отклики, должен вводиться из понятия абсолютной величины вектора. Вместе с тем метрический тензор в пространстве сети существует и в отсутствии каких-либо векторов. Для сети замкнутых путей метрический тензор Y_c имеет вид, определяемый формулой тензорного анализа сетей (23), а для сети разомкнутых путей метрический тензор Z_c определяется формулой (24).

Если считать все веса ветвей (сопротивления) равными единицам, то по формуле (23), используя подматрицу контуров, получим метрический тензор Y с для левой сети следующего вида, который одновременно является метрическим тензором замкнутых путей правой сети.

Для расчета метрических тензоров используется подматрица ^mС левой контурной сети, состоящая из верхних трех строк, и подматрица ^m С правой двойственной контурной сети, состоящая из нижних двух строк.

1			2	3	4	5
	1	0,63	0,38	-0,13	0,13	0,25
	2	0,38	0,63	0,13	-0,13	-0,25
Y с =	3	-0,13	0,13	0,63	0,38	-0,25
	4	0,13	-0,13	0,38	0,63	0,25
	5	0,25	-0,25	-0,25	0,25	0,50

Аналогично, для правой, двойственной сети, используя подматрицу контуров, получим метрический тензор Zс по формуле (24) следующего вида, который одновременно является метрическим тензором разомкнутых путей левой сети.

	1	2	3	4	5
1	0,38	-0,38	0,13	-0,13	-0,25
2	-0,38	0,38	-0,13	0,13	0,25
Z с =       3	0,13	-0,13	0,38	-0,38	0,25
4	-0,13	0,13	-0,38	0,38	-0,25
5	-0,25	0,25	0,25	-0,25	0,50

Существует инвариант двойственности, который состоит в постоянстве суммы метрических тензоров двойственных сетей при изменении структуры соединения ветвей. Данный инвариант двойственности является свойством структуры пространства. Инвариант двойственности при изменении структуры является основой закона сохранения потока энергии. Сумма метрических тензоров (матриц решения) двойственных сетей равна метрическому тензору простейшей сети из свободных, несоединенных ветвей.

Y¹ с + Y ¹ с = Y 0

	1	2	3	4	5		1	2	3	4	5		1	2	3	4	5
1	0,63	0,38	-0,13	0,13	0,25	1	0,38	-0,38	0,13	-0,13	-0,25	1	1	0	0	0	0
2	0,38	0,63	0,13	-0,13	-0,25	2	-0,38	0,38	-0,13	0,13	0,25	2	0	1	0	0	0
3	-0,13	0,13	0,63	0,38	-0,25	+ 3	0,13	-0,13	0,38	-0,38	0,25	= 3	0	0	1	0	0
4	0,13	-0,13	0,38	0,63	0,25	4	-0,13	0,13	-0,38	0,38	-0,25	4	0	0	0	1	0
5	0,25	-0,25	-0,25	0,25	0,50	5	-0,25	0,25	0,25	-0,25	0,50	5	0	0	0	0	1

Рассмотрим выполнение инварианта двойственности при изменении структуры сети.

На рисунке 3 узел С в сети слева разделен на два узла С1 и С2 в сети справа.

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

том 15 № 1 (42), 2019, ст. 1

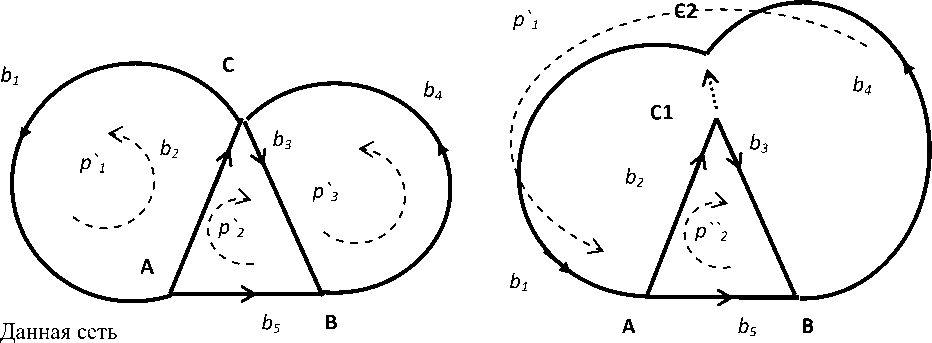
Измененная сеть

Рис. 3. Сеть из 5 ветвей с изменением структуры: узел С в сети слева разделен на узлы С1 и С2 в сети справа

Этим сетям соответствуют матрицы преобразования путей базиса свободных ветвей в базис путей в связанных ветвях. Матрица преобразования C 1 левой сети (три контура) и матрица преобразования С 2 правой сети с изменением структуры, с разделенным узлом С на узлы С1 и С2, (два контура).

p 1

p 2

p 3

p 4

p 5

p 1

p 2

p 3

p 4

p 5

p 1 `

1

1

m

p 1 ``

1

1

1

1

m

p 2 `

1

1

–1

m

p 2 ``

1

1

-1

m

C 1 = p 3 `

1

1

m

С 2 =p 3 ``

1

1

j

p 4 `

1

j

p 4 ``

1

j

p 5 `

1

j

p 5 ``

1

j

Для расчета метрических тензоров используется подматрица ^mС 1 левой контурной сети, состоящая из верхних трех строк, и подматрица ^mС 2 правой контурной сети с разделенным узлом, состоящая из верхних двух строк.

Метрический тензор Y¹ с для левой сети уже получен в предыдущем примере:

1			2	3	4	5
	1	0,63	0,38	-0,13	0,13	0,25
	2	0,38	0,63	0,13	-0,13	-0,25
Y 1 с =	3	-0,13	0,13	0,63	0,38	-0,25
	4	0,13	-0,13	0,38	0,63	0,25
	5	0,25	-0,25	-0,25	0,25	0,50

Получим метрический тензор Y² с для правой сети, с разделенным узлом:

1			2	3	4	5
	1	0,38	0,13	0,13	0,38	0,25
	2	0,13	0,38	0,38	0,13	-0,25
2 с	3	0,13	0,38	0,38	0,13	-0,25
	4	0,38	0,13	0,13	0,38	0,25
	5	0,25	-0,25	-0,25	0,25	0,50

На рисунке 4 узлы D и C в двойственной сети слева соединены в один узел D-С в двойственной сети справа.

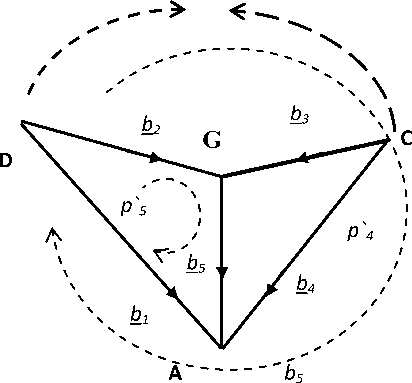
Исходная двойственная сеть

Рис. 4. Двойственная сеть из 5 ветвей с изменением структуры:

узлы D и C в сети слева сливаются в один узел в сети справа (направление соединения показано стрелками пунктиром)

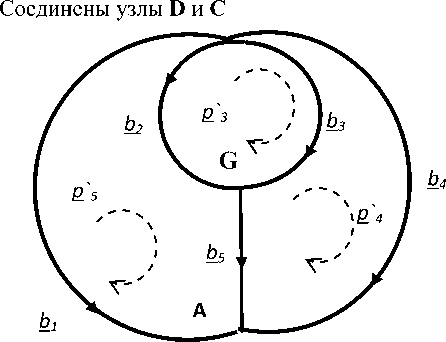
Двойственная сеть с измененной структурой

Этим двойственным сетям соответствуют матрицы преобразования путей базиса свободных ветвей в базис путей в связанных ветвях. Матрица преобразования C1 двойственной сети (два контура) и матрица преобразования С2 двойственной сети с изменением структуры (три контура)

p 1		p 2	p 3	p 4	p 5
p 1 `	1					j
p 2 `	-1	1				j
С 1 = p 3 `	1	–1	1			j
p 4 `			–1	1	–1	m
p 5 `	–1	1			1	m

p 1	p 2	p 3	p 4	p 5
p 1 ``     1				j
p 2 ``    -1	1			j
С 2 = p 3 ``	–1	1		m
p 4 ``		–1	1	–1  m
p 5 ``   –1	1			1   m

Для расчета метрических тензоров используется подматрица ^m С 1 левой контурной двойственной сети, состоящая из нижних двух строк, и подматрица ^m С 2 правой контурной двойственной сети с разделенным узлом, состоящая из нижних трех строк.

Метрический тензор Y ¹ с для левой двойственной сети уже получен выше:

1          2          3          4          5

1	0,38	-0,38	0,13	-0,13	-0,25
2	-0,38	0,38	-0,13	0,13	0,25
3	0,13	-0,13	0,38	-0,38	0,25
4	-0,13	0,13	-0,38	0,38	-0,25
5	-0,25	0,25	0,25	-0,25	0,50

Метрический тензор Y ² с для правой двойственной сети получим по формуле (23):

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

том 15 № 1 (42), 2019, ст. 1

1          2          3          4          5

0,63	-0,13	-0,13	-0,38	-0,25
-0,13	0,63	-0,38	-0,13	0,25
-0,13	-0,38	0,63	-0,13	0,25
-0,38	-0,13	-0,13	0,63	-0,25
-0,25	0,25	0,25	-0,25	0,50

Инвариант двойственности состоит в том, что сумма метрических тензоров двух двойственных сетей при изменении структуры соединения ветвей постоянна и равна метрическому тензору простейшей сети из отдельных ветвей. Пока в сетях нет никаких потоков энергии, инвариант двойственности отражает свойство структуры самого пространства. Вместе с тем инвариант двойственности при изменении структуры является основой закона сохранения потока энергии.

Y² с + Y ² с = Y 0

	1	2	3	4	5	1		2	3	4	5	1		2	3	4	5
1	0,38	0,13	0,13	0,38	0,25	1	0,63	-0,13	-0,13	-0,38	-0,25	1	1	0	0	0	0
2	0,13	0,38	0,38	0,13	-0,25	2	-0,13	0,63	-0,38	-0,13	0,25	2	0	1	0	0	0
3	0,13	0,38	0,38	0,13	-0,25	+ 3	-0,13	-0,38	0,63	-0,13	0,25	= 3	0	0	1	0	0
4	0,38	0,13	0,13	0,38	0,25	4	-0,38	-0,13	-0,13	0,63	-0,25	4	0	0	0	1	0
5	0,25	-0,25	-0,25	0,25	0,50	5	-0,25	0,25	0,25	-0,25	0,50	5	0	0	0	0	1

Закону структуры, инварианту двойственности соответствует закон сохранения потока энергии, который выражается как постоянство суммы рассеиваемых мощностей при изменении структуры двух двойственных электрических цепей. Мощность (поток энергии) при изменении структуры двух двойственных сетей не меняется. Или сумма мощности в данной сети ^mP данная и мощности в двойственной сети ^mP двойст. равна мощности в простейшей сети ^mP 0 с теми же источниками тока или напряжения:

• ^mP данная + ^mP двойст. = ^mP 0

Этот объективно существующий физический закон соответствует инварианту двойственности структуры сетей. Однако путь к этому закону лежал через постулат Крона об инвариантности мощности при соединении отдельных ветвей простейшей сети в связанную сеть. Этот постулат не выполняется, за это Крона критиковали. Но тензорный метод, основанный на неправильном постулате, дает правильные результаты расчета сетей и сетевых моделей сложных систем. Таким образом, противоречие в постулате Крона об инвариантности мощности нашло свое разрешение через двойственные сети.