Закон сохранения потока энергии и сетевые модели для проектирования систем безопасности объектов нефтепереработки

Введение: теория электрических машин и управление обществом

Под руководством Побиска Гергиевича Кузнецова и при поддержке Льва

Тимофеевича Кузина представители МИФИ, МФТИ и МИЭМ, перевели в 1973-1978 гг.

книгу Габриэля Крона «Тензорный анализ сетей» [6]. Крон впервые рассмотрел переход от одной структуры сети с потоком энергии к другой структуре сети. Переход обеспечивает группа матриц преобразования структуры, которые составляют тензор структуры, с инвариантом мощности. Крон разработал также диакоптику - метод создания сетевых моделей и расчета сложных систем по частям [5]. Токи в контурах связанной сети Крон с помощью матрицы преобразования выражал через токи в простейшей сети из отдельных ветвей. Постулируя, что уравнение связанной сети имеет такую же форму, что и простейшей сети, можно по решению простой сети получить формулами преобразования решение сложной сети.

Используя этот аппарат, Крон создал модели в виде эквивалентных электрических цепей для физических и технических систем. Это модели строительных конструкций, ядерного реактора, диафрагмы турбин, транспортной задачи. Модели уравнений Максвелла, Шредингера, Навье-Стокса, многоатомных молекул. Электрические машины, которые сами суть двумерные сети (обмотка представляет поверхность распространения магнитного потока), также представлены одномерными цепями. Последние работы Крона посвящены созданию многомерных (полиэдральных) сетей с волновым возбуждением, которые обладают свойством самоорганизации, и могут стать технической основой искусственного мозга. Повторить эти результаты пока не удалось [1, 4, 14].

П.Г. Кузнецов считал метод Крона введением в теорию проектирования прикладных задач в технике, экономике, управлении. Метод Крона критиковали на протяжении полувека за противоречивость - мощность при изменении соединений в сети не постоянна, а матрицы преобразования прямоугольные, т.е. не имеют обратных и не образуют группу. Однако метод давал правильные результаты при расчете цепей и электрических машин [1]. Ныне теория электрических машин Крона считается классикой [9]. В ее основе лежит преобразование потока энергии при изменении структуры. Это позволяет от уравнений обобщенной машины (это простейшее устройство электромеханического преобразования энергии с двумя обмотками статора и двумя обмотками ротора) с помощью матриц преобразования переходить к уравнениям электрических машин любой сложности.

Кузнецов хотел создать аналогичную «обобщенную машину» для общества (простая ячейка производства, потребления и денежных потоков, элемент социально-экономической системы), и на ее основе переходить с помощью матриц преобразования к моделированию и управлению устойчивым развитием сложных субъектов: предприятия, региона, страны, планеты.

Крон показал, что поведение электрической машины в любом режиме описывают уравнения одного типа, отличие в том, что усложняется пространство и соответствующий метрический тензор.

Стационарный (устойчивый) режим работы электрической машины описывает простое уравнение типа закона Ома, где тензор сопротивления R αβ определяет метрику пространства Декарта.

Режим ускорения при переходе от покоя к устойчивой работе описывает такое же по форме уравнение, но тензор сопротивления R αβγ определяет метрику криволинейного пространства Римана. При этом обычное дифференцирование в уравнениях поведения заменяется ковариантным дифференцированием.

Режим качаний, когда стационарное вращение сбивается от устойчивого режима к опасным колебаниям, описывает такое же по форме уравнение, но метрический тензор R αβγδ становится четырех индексным, и определяет метрику криволинейного пространства с кручением Римана-Кристоффеля [13].

Аналогично необходимо создать метод управления обществом в стационарном, устойчивом развитии. Затем трансформировать его к управлению в переходных процессах, например, при переходе к очередному укладу на основе новых технологий. Затем на этой основе создать метод управления обществом в период «качаний», когда внешние или внутренние силы отклоняют систему от режима устойчивого развития. Это позволит создать метод управления обществом для выхода из финансовых и экономических кризисов. Или прогнозировать опасности отклонений от устойчивого развития.

В работах отечественных ученых намечен определенный путь применения методов Крона для расчета балансового планирования [2-4], проектирования инновационного регионального развития [10], проектирования технических систем [11].

Сети

Ветвь есть отрезок линии с границами-узлами. Сеть состоит из ветвей, которые могут иметь веса, и соединяться границами-узлами. Это одномерная сеть. Соединения ветвей составляют структуру сети. Изменения соединения ветвей есть изменение структуры сети. Ветви образуют пространство сети.

Координатами этого пространства являются пути – последовательности соединенных ветвей. Путь проходит по ветви от одной границы до другой, продолжается в ветви,

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.) соединенной с ней и т.д. Путь, который вернулся после прохождения ветвей в узел начала – это замкнутый путь, контур; иначе – разомкнутый.

Один путь можно выражать через другие пути, комбинируя составляющие их ветви. Набор линейно независимых путей составляет базис в пространстве сети. Базисы контуров и разомкнутых путей определяют подпространства замкнутых и разомкнутых путей. Эти подпространства ортогональны и дополняют друг друга до полного пространства сети.

Изменение путей при изменении структуры есть преобразование координат. Обозначим количество ветвей в сети через n , узлов – J , подсетей – s, независимых замкнутых путей – m , а разомкнутых путей – j . В каждой сети значения этих параметров, которые дают размерности подпространств замкнутых и разомкнутых путей, определяют соотношения:

j = J – s,                                          (1)

n = m + j.                                       (2)

Изменение структуры состоит в изменении числа узлов в сети – одни соединяются, другие разъединяются. При разделении узла на два узла исчезает контур, но возникает разомкнутый путь, и наоборот; меняются размерности их подпространств.

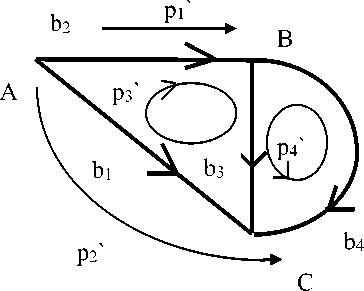
При изменении структуры базисные пути в новой сети можно выразить через базисные пути в старой сети. Коэффициенты в таком выражении образуют матрицу преобразования путей. Это матрица преобразования структуры. В качестве примера рассмотрим рис.1. Справа, на рис. 1б четыре свободные ветви-контура. Из соотношений (1) и (2) получим в этой сети узлов J = 4 , четыре подсети s = 4, т.е. нет разомкнутых путей j = J – s = 4 – 4 = 0. Есть четыре контура m = n – j = 4 – 0= 4 . Слева, на рис.1а, эти ветви связаны в сеть. В этой новой сети есть три узла, одна подсеть, т.е. два разомкнутых пути и два конура.

а)

_b         b 2            b 3             ^b4

p 1            p 2             p 3              p 4

б)

Рис. 1. Базис замкнутых, m и разомкнутых, j путей в сети а – базисные пути в связанной сети; б – базисные пути в свободной сети

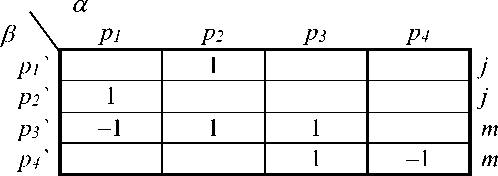
Коэффициенты выражения базиса путей в связанной сети через пути в свободных ветвях составляют матрицу преобразования путей: рр' = Cp'ара:

е в

jc mc

В матрице преобразования С строки показывают, какие ветви, с какой ориентацией, составляют данный путь. Элементы столбцов показывают, в какие пути, с какой ориентацией входит данная ветвь. Матрица С состоит из двух подматриц, описывающих преобразование замкнутых тС и разомкнутых jC путей. Она используется для расчета контурной сети, сети с внутренним воздействием. Это расчет токов в ветвях при заданных источниках ЭДС. Крон связывал независимые контурные токи в простейшей и связанной сети, поэтому его матрица преобразования является транспонированной к рассматриваемой здесь.

Ортогональная к С матрица, которую обозначим как А: А = (С)^, описывает преобразование взаимного (дуального) базиса путей при изменении структуры.

а в \   pi______Р2______рз______Р4

Р 1 ' А = (С)- 1    =    р? Рз' Р4'		1	–1	–1	j .        А      т С J m       тА     J С т
	1		1	1
		1	1	1
				–1

Как известно, каждый вектор взаимного базиса ортогонален всем векторам прямого базиса [15, с. 432]. Вектор взаимного базиса можно рассматривать как две эквипотенциальные поверхности, определяющие разность потенциалов, т.е. напряжение. Крон и рассматривал эту матрицу, как преобразование напряжений. Матрица А используется для расчета сети с внешним воздействием; в электротехнике это узловой метод расчета напряжений на ветвях при заданных в узлах источниках тока.

Крон полагал, что строки и столбцы матрицы А не имеют такой наглядной интерпретации, как у матрицы С. Оказалось, что матрица А исходной сети является матрицей

С двойственной сети. Для получения формул преобразования величин в сети введем понятие вектора, который возникает в сети, как поток воды в трубе.

Пусть на сеть наложен вектор d , который располагается в ветвях, и представлен компонентами d ^a в координатах-путях вектора базиса pa.

d = da pa(3)

Вектор можно интерпретировать как поток энергии в электрической цепи. При изменении соединений ветвей получим новую структуру сети; тогда тот же вектор будет представлен в новом базисе p a' компонентами d ^a :

d = d«pa'(4)

Выразим компоненты вектора d в новой структуре, используя преобразование путей pp' = Cp' apa(5)

Приравняв выражения вектора в (3) и (4), и подставляя (5), получим:

de = (Cp' a)-1t da = Авa da(6)

т.е. компоненты внедренного в сеть вектора при изменении структуры изменяются противоположно, контравариантно относительно компонент путей базиса.

Если ввести квадрат величины вектора d как произведение ковариантных и контравариантных компонент:

I d I2 = dada,(7)

то получим закон преобразования ковариантных компонент при изменении структуры от старой сети к новой сети:

I d I2 = da da = da' da',(8)

откуда, подставляя выражение (6) для ковариантных компонент d a вектора d :

da' = Cp- a da(9)

т.е. компоненты d a преобразуются так же, как компоненты вектора базиса путей, являются ковариантными компонентами вектора потока энергии. Линейный характер преобразования компонент вектора d в пространстве структуры показывает, что они являются тензорами.

Для электрической цепи компоненты абстрактного вектора d имеют аналогии: ковариантным компонентам соответствует напряжение, контравариантным компонентам соответствует ток. Квадрату величины вектора d соответствует рассеиваемая в цепи мощность. Если заданы веса ветвей, то их можно рассматривать как метрику (сопротивление в цепи), заданную матрицей метрического тензора, обозначим Zap. Метрический тензор в сети, как в векторном пространстве, связывает ковариантные и контравариантные компоненты вектора (аналог закона Ома в цепи), например:

d a = Z ap d ^e                                       (10)

Подставляя сюда (6) и (9) получим формулу преобразования метрического тензора при изменении структуры от старой сети к новой сети:

Z a'P' = C a'^a Z ap C p-P t                                         (11)

Вектор потока энергии в сети определяется заданием одного вида компонент, например d a , в качестве источника воздействия. Тогда контравариантные компоненты второго вида, например, d ^a , являются откликом, их величина определяется метрикой Z ap, решением уравнения (10). Базисом структуры являются замкнутые пути, а преобразования осуществляются матрицей ^mC. Этому соответствует контурный метод расчета цепи.

Если воздействие задают компоненты d ^a , то компоненты d a - отклик, величина которого определяется метрикой Y ^ae = (Z ap У¹. Тогда компоненты отклика получаются решением уравнения d ^a = Y ^ae d a , где Y - аналог матрицы проводимостей. В этом случае базисом являются независимые разомкнутые пути, а преобразования осуществляются матрицей jA. Этому соответствует узловой метод расчета цепи .

Предполагается, что уравнения поведения системы имеют одинаковую форму для любой структуры соединения элементов. Наиболее простая сеть – это свободные ветви. Преобразование к связанной сети (величины обозначим штрихами) выполняют матрицы преобразования путей ^mC или ^jA .

Пусть имеются свободные ветви-контуры, их уравнение поведения (10). Соединим ветви в новую, связанную сеть, уравнение поведения которой:

d a- = Z a-p- d ^e                                           (12)

Матрица mC выражает пути в связанной сети через пути в свободных ветвях. Подставим в (12) формулы преобразования (6), (9) и (11) и, решая это матричное уравнение, получим выражение откликов в путях связанной сети через воздействия в свободных ветвях de' = (Ч'„" Zap mCpet)1 mG" da                        (13)

Перейдем от откликов (токов) в путях-контурах к измеримым величинам в отдельных ветвях связанной цепи, которые обозначим d ^в с .

d ^в с = ^mC a-^a t d^в' = ^mC a^a t ( " C a-^a Z ap ^mCp ^e t )^{1 m}C a^a d a

Выражение перед вектором источников d a обозначим Y c и назовем матрицей решения. Это метрический тензор связанной контурной сети.

Y c = m C a'^a t ( m C a'^a Z ap ^тСр ^в t )^- m C a^a                             (15)

Умножение Y c на произвольный вектор воздействия позволяет сразу получить отклики в ветвях связанной сети. Для контурной электрической цепи воздействие – это источники напряжения, ЭДС e a , а отклики - токи в ветвях i ^a с .

Мощность, рассеиваемая в простейшей цепи   mPo = iao eao равна мощности источников, а в ветвях связанной цепи mPc = ea 1% =mP'.

Таким образом, получили уравнения контурного метода расчета цепи для источников ЭДС, заданных в свободных замкнутых ветвях.

Воздействия и отклики в сети, как токи и напряжения в электрической цепи, подчиняются законам Кирхгофа, что является проверкой правильности решения.

В сети двойственны (в смысле взаимного дополнения) замкнутые и разомкнутые пути, токи и напряжения, сопротивления и проводимости. Такими двойственными заменами получим уравнения решения сети для базиса разомкнутых путей. Матрица ^mC заменяется матрицей ^jA , а матрица Z – матрицей Y. Метрический тензор связанной узловой сети обозначим Z c и назовем матрицей решения:

Z c = ^jA^a' a t (A ^aa Y ^ap A#' t )^- А в                     (16)

Умножение Z c на произвольный вектор воздействия позволяет сразу получить отклики в ветвях связанной сети. Для электрической цепи это вектор источников тока, I ^е , заданных в свободных разомкнутых ветвях, а отклики – напряжения на ветвях связанной сети Ea^c.

Мощность, рассеиваемая в простейшей цепи ^jP o = I ^a o E a o равна мощности источников, а в ветвях связанной цепи ^jP_c = E a 1 % = ^jP' .

Двойственная сеть и закон сохранения потока энергии

К заданной сети существует двойственная сеть, в которой каждому замкнутому пути соответствует разомкнутый путь, а каждому разомкнутому пути соответствует замкнутый путь. Ее величины обозначим подчеркиванием. Размыканию путей в данной сети соответствует замыкание пути в двойственной сети, и наоборот. Матрица А данной сети является матрицей С для двойственной сети, в которой подматрицы замкнутых и разомкнутых путей меняются местами. И наоборот, матрица С данной сети является матрицей А для двойственной сети.

Оказалось, что существует инвариант двойственности, который состоит в постоянстве суммы метрических тензоров (матриц решения) двух двойственных сетей при изменении их структуры. В физике этому инварианту соответствует закон сохранения потока энергии, который выражается в постоянстве суммы рассеиваемых мощностей двух двойственных электрических цепей при изменении их структуры. Это и является разгадкой инварианта мощности Крона – мощность меняется при изменении соединений в одной сети, но постоянна при изменении соединений в двух сетях с двойственной структурой.

Таким образом, матрица решения контурной двойственной сети соответствует матрице решения заданной узловой сети.

Y c = ^mC a ^at ( m C^ Z ae m C e^" ⁷ " C „^a = ^jA^a' a t (A « a Y ^a A, /'t )"^{1 j} A/fi'     (1T)

Аналогично, матрица решения двойственной узловой сети соответствует матрице решения контурной заданной сети.

Z c = ^jA “a t (A ^a'a W j A ef t )^{1 j}A je' = ^mC a^a t ( m C a'^a Z ae m C_P ^e t ) " ^mC a^a  (18)

Данный инвариант (закон сохранения потока энергии), который автор открыл в 1981 году, рассматривается в [1-4, 7]. При этом для замкнутых систем сумма прямых метрических тензоров двух двойственных сетей равна метрическому тензору свободных контуров, а для открытых систем сумма обратных метрических тензоров двойственных сетей равна тензору свободных разомкнутых ветвей.

Этот закон находится в ряду других законов сохранения, т.е. физических законов, согласно которым некоторое свойство замкнутой системы остается неизменным при каких-либо изменениях в системе. Всеобщность законов сохранения механических величин (энергии, импульса, момента), связана с тем, что им соответствуют свойства симметрии пространства-времени (мира). Согласно теореме Нётер, сохранение энергии связано с однородностью времени, т.е. с физические законы инвариантны относительно изменения начала отсчёта времени. Сохранение импульса и момента количества движения связано соответственно с однородностью пространства (инвариантность относительно пространственных сдвигов) и изотропностью пространства (инвариантность относительно вращений пространства). Закон сохранения потока энергии связан с двойственностью структуры пространства. Он намекает на существование двойственного пространства.

В простейшем виде, при единичной метрике, т.е. если собственные сопротивления ветвей равны единицам, а взаимные равны нулю, то Z и Y - единичные матрицы, Z = Y = I, и

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.) при отсутствии потоков в сети, инвариант двойственности для замкнутых путей приобретает простой абстрактный вид:

I = ^mC t (^mC ^mC t )^{-1 m}C + ^jA t (^jA ^jA t )^{-1 j}A                     (19)

Здесь I – единичная матрица. Это фундаментальное свойство структуры сетей выражается отношениями между матрицами преобразования путей, и не зависит от физических свойств ветвей, от потоков энергии.

Пример выполнения закона сохранения потока энергии

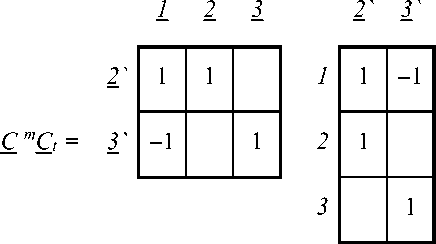
Рассмотрим пример выполнения инварианта при изменении структуры двух двойственных сетей из трех ветвей, представленных на рис. 2.

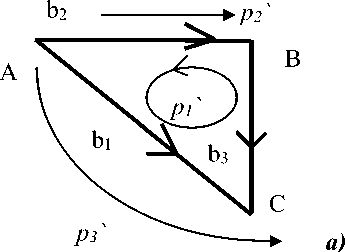
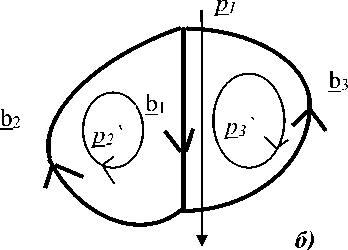
Рис. 2. Двойственные сети а – заданная сеть: один контур p1`, два разомкнутых пути p2` и p3`; б - двойственная сеть: два контура рз' и рз', один разомкнутый путь pi'

Матрица преобразования путей простейшей сети к путям в заданной сети, которые показаны на рис. 2а, имеет следующий вид:

Q f

p 1         p 2         p 3

p 1 `	1	–1	1	m	mC
p 2 `		1		j
p 3 `			1	j	jC

Матрица преобразования путей простейшей сети к путям в двойственной сети, которые показаны на рис. 2б, имеет следующий вид:

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»

вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.)

О в^ = А д^а

Р 1

P 2

P 3

p i

P 2

P 3

1
1	1
–1	1

m

j

jC = mA

j

mC = jA

Получим матрицу решения данной контурной сети при единичной метрике:

Y c = ^mC a'“ t ( m C a' ^a Z ap ^mC p^P t )^{1 m}C a^a = ^mC t ( m C ^mC t )^{1 m}C

Сначала вычислим выражение в скобках и получим обратную матрицу:

1'

^mC ^mC t =  1'

1	2	3
1	–1	1

1'

1'

–1

1'   3

m Y' = ( m e m e t )¹ =

1'

1/3

^mC t ( m C ^mC t )^{1 m}C =   2

1'

–1

1'

1'  1/3

1'

1	2	3
1	–1	1

1/3	–1/3	1/3
–1/3	1/3	–1/3
1/3	–1/3	1/3

Получим матрицу решения двойственной контурной сети при единичной метрике:

Y c = ^mC a'« t CC a-^a Z ap m C e^ ) " ^{1 m} Ca^a = ^jA _t (A ^jA t )^{1 j}A = Z c

Сначала вычислим выражение в скобках и получим обратную матрицу:

m

2'   3'

2'

3'

2/3	1/3
1/3	2/3

2'   3'

3'

( m C ^mC t )¹ =   2'

2/3	–1
–1	2/3

Далее получим Y c = ^m C t (^m C ^m C t )^{-1 m} C =

2` 3` 1 2 3 1 1 –1 2` 3' 1   2 3 1   2/3 1/3 –1/3 2 1 2`  2/3 –1        2` 1      1 =   2   1/3 2/3 1/3 3 1 3`  –1 2/3        3` –1 1 3  –1/3 1/3 2/3 Сложив матрицы решения (метрические тензоры) данной и двойственной сети получим единичную матрицу, что подтверждает выполнение инварианта двойственности Yc + Yc = I:

	1	2	3			1	2	3			1	2	3
1	1/3	–1/3	1/3		1	2/3	1/3	–1/3		1	1
2	–1/3	1/3	–1/3	+	2	1/3	2/3	1/3	=	2		1
3	1/3	–1/3	1/3		3	–1/3	1/3	2/3		3			1

Данный пример показывает, как выполняется инвариант двойственности. В физике он представляет собой постоянство суммы рассеиваемых мощностей в двух двойственных сетях при изменении их структуры. Т.е. инварианту двойственности соответствует закон сохранения потока энергии при изменении структуры двойственных сетей.

На том же примере из трех ветвей рассмотрим изменение мощности при соединении свободных ветвей в связанную сеть – для заданной сети и двойственной сети.

Задан вектор источников ЭДС, которые имеют значения в каждой ветви.

e° a

1       2       3

2

1

3

Свободные ветви пусть будут контуры, подобно тем, которые даны на рис. 1. В свободных ветвях при единичных сопротивлениях откликами будут токи i ^a oc и напряжения e a , численно равные значениям источников и друг другу, т.е.

i ^a °c

1      2      3

с0 e a

1      2      3

2

1

3

Мощность mP0 в сети свободных ветвей равна mP° =   ia0c eac0 = 2 х 2 + 1 х 1 + 3 х 3 = 14.

Напомним, что по повторяющимся верхним и нижним индексам, в данном случае это a, предполагается суммирование.

Для расчета откликов (токи i ^a c и напряжения e a ⁰ ) и мощности в связанных сетях используем полученные выше матрицы решения (метрические тензоры) связанных сетей.

Для заданной связанной сети получим токи i ^a c и напряжения ea^c

iac = Yc e°a = mC (mC mC t)1 mC e°a = eac 1 2 3 e°a iac eac 1 1/3 –1/3 1/3 1 2 1 4/3 1 4/3 iac =   2 –1/3 1/3 –1/3 2 1 =   2 –4/3 =    2 –4/3 3 1/3 –1/3 1/3 3 3 3 4/3 3 4/3 Мощность, mPc, рассеиваемая в ветвях заданной связанной сети равна mPc = iac eac = (4 х 4 +(-4) х(-4) + 4 х 4)/(3 х 3) = 16/3.

Эта мощность меньше, чем в простейшей (примитивной) сети свободных ветвей. Таким образом, постулат Крона об инварианте мощности при соединении отдельных ветвей в связанную сеть [6] не выполняется.

Для двойственной связанной сети получим токи iac и напряжения eac iac = Yc e°a = mCt (mC mC t)- mC e°a = вас

	1	1	2	3	1	e ° a	1	i a c	1		e a
		2/3	1/3	–1/3		2		2/3			2/3
i a c =	2	1/3	2/3	1/3	2	1	=    2	7/3	=	2	7/3
	3	–1/3	1/3	2/3	3	3	3	5/3		3	5/3

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.) Мощность, mPc, рассеиваемая в ветвях двойственной связанной сети равна mPc = iαc eαс = (2 х 2 +7 х 7 + 5 х 5)/(3 х 3) = 26/3.

Эта мощность меньше, чем в простейшей сети из свободных ветвей. Таким образом, постулат Крона об инварианте мощности при соединении отдельных ветвей в двойственную связанную сеть также не выполняется.

Вместе с тем рассеиваемая мощность в сети свободных ветвей равна сумме рассеиваемых мощностей в заданной связанной сети и двойственной связанной сети mP0 = mPc + mPc = 16/3 + 26/3 = 42/3 = 14.

Данный пример демонстрирует постоянство рассеиваемой мощности при изменении структуры (в данном случае – связывании свободных ветвей в сеть) двух двойственных сетей. Это и есть выполнение закона сохранения потока энергии (измеряемого мощностью) при изменении структуры двойственных сетей. Далее необходимо обобщить данный закон на сети из поверхностей – двумерные сети, сети из объемов – трехмерные сети, и соответствующее возбуждение электромагнитными волнами.

Расчет сети при изменении структуры – обобщенная диакоптика

При изменении структуры сети необходимо заново выводить уравнения поведения и решать их. Если размерность сети большая, то расчет для каждой новой структуры трудоемок. Тензорный метод позволяет сделать расчет одного варианта структуры, а затем преобразовать его в решение сети с другой структурой. Например, для анализа решений при различных отключениях или переключениях элементов установки, которые могут приводить к авариям. По матрице решения старой сети и матрице изменения решения можно получить матрицу решения сети с новой структурой.

Возможные изменения структуры: разделение сети на части или соединение связанной сети из частей, разъединения или соединения внутри сети; все это при внешних воздействиях (базис разомкнутых путей) или внутренних воздействиях (базис замкнутых путей), для данной сети или для двойственной сети [2-4]. Формулы расчета сетей при всех изменениях структуры сетей получены автором в общем виде, аналитически, т.е. выведены из формул тензорного анализа сетей с применением инварианта двойственности. Крон получил формулы расчета сетей по частям для так называемых пуассоновского типа (в сети мало заземлений) и диффузионного типа (в сети много заземлений). Его подход инженерный, конструктивный, поэтому в диакоптике [5] много эвристических приемов, дополнительных операций и ограничений.

Изменения структуры – это изменение числа узлов. При слиянии двух узлов возникает контур, исчезает разомкнутый путь. При разделении узла на два узла контур исчезает, возникает разомкнутый путь. Это меняет базисы контуров и разомкнутых путей, меняется размерность их подпространств. В соответствии с (1) и (2) надо также учитывать изменение числа подсетей. Для потока в сети возникают новые пути или закрываются другие пути. Это меняет поведение сети и представленной ей системы.

В двойственной сети при этом происходят обратные изменения. Матрица изменений структуры содержит только те пути, которые изменились. Например, все контуры, ставшие разомкнутыми путями. Или все разомкнутые пути, ставшие контурами. Входящие в эти пути ветви составляют сеть изменений структуры . Сеть изменений меньше полной сети, поэтому ее расчет легче полного расчета. Главное состоит в том, что изменения в структуре отображаются в двойственной сети к сети изменений.

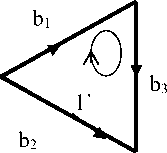
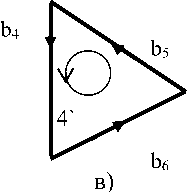
В матрице преобразования при соединении подсетей в сеть часть разомкнутых путей замыкается. При этом появляются новые элементы, соответствующие ветвям, через которые замыкается контур. Например, на рис. 3 представлена сеть из 10 ветвей. При расчете по частям сеть разделена на три подсети – два треугольника и сеть соединений, квадрат. Эти подсети показаны наверху. Внизу – связанная сеть, где квадрат соединяет треугольники. Пути 8` и 9`, которые в квадрате были разомкнуты, стали контурами в связанной сети.

а)

b 9

9`

b 7

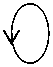
7`

Vb10

b 8

V p 8`

А

Б

б)

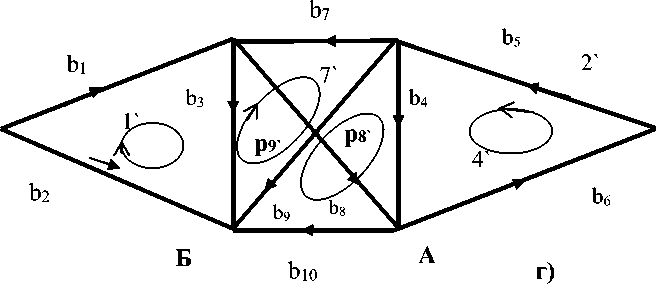
Рис. 3. Соединение подсетей в сеть с помощью r-сети соединений Подсети: а) сеть 1, б) r-сеть соединений, в) сеть 2;

г) связанная сеть, в которой контуры 8`и 9`включают новые ветви из r-сети

Матрица преобразования для всех трех отдельных подсетей C¹ имеет вид.

		1	2	3	4	5	6	7	8	9	10
	1`	1	–1	1								m
	2`		1									j
	3`			1								j
	4`				1	1	1					m
C1 =	5`					1						j
	6`						1					j
	7`							1	–1	1	1	m
	8`								1			j
	9`									1		j
	10`										1	j

Блоки подсетей выделены двойной линией и располагаются по главной диагонали. Первая строка в каждой – контур, остальные разомкнутые пути. Матрица преобразования связанной сети C² имеет несколько иной вид.

	1	2	3	4	5	6	7	8	9	10
1`	1	–1	1							m
2`		1								j
3`			1							j
4`				1	1	1				m
C2 =   5`					1					j
6`						1				j

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам

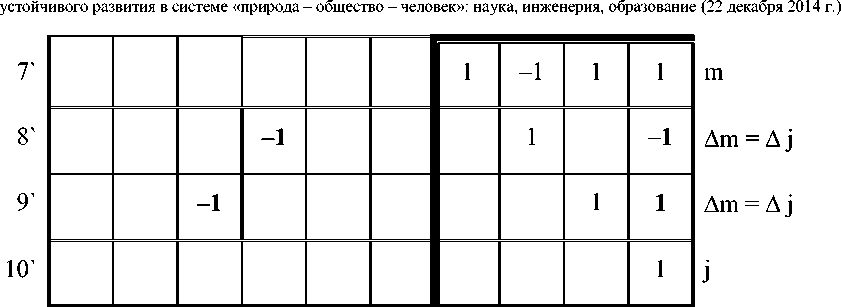
Здесь строки 1`, 4`, 7` составляют матрицу <sup>m</sup>C<sup>1</sup> подсетей. Вместе со строками 8` и 9`, представляющими Δ C с измененными путями Δ j = Δ m , т.е. с разомкнутыми путями, которые превратились в контуры, они составляют матрицу ^mC² связанной сети. В матрице изменений (измененных путей) Δ C^2r (в строках 8 и 9) добавляются элементы, представляющие ветви из r -сети и подсетей, которые замыкают в связанной сети новые контуры. Эти элементы выделены жирным шрифтом [3, с. 297]. При расчете по частям изменения в метрике данной сети вносятся с помощью матрицы решения двойственной сети к сети изменений.

Данный математический аппарат является основой алгоритмов для организации параллельных вычислений на сетевых моделях физических, технических, экономических систем. Возможны любые изменения в структуре при любых источниках.

Инвариант двойственности, двойственная сеть помогает решить проблему вырождения, т.е. когда при изменении структуры возрастает число переменных (путей данного типа). Например, есть источники тока, и возрастает число переменных, т.е. разомкнутых путей. Или есть источники напряжения, и возрастает число переменных, т.е. контуров. При этом так меняется размерность подпространств замкнутых и открытых путей в сети, что придется как бы из линии перейти в плоскость, или из плоскости в пространство.

Однако при этом происходит обратное изменение этих размерностей в двойственной сети. Таким образом, можно решить задачу в этой сети, с переходом к меньшему числу переменных, числу измерений, а затем с помощью инварианта двойственности получить решение искомой задачи. Рассмотрим общий метод расчета сети при изменении структуры.

Задача состоит в получении матрицы решения для новой структуры по матрице решения старой структуры и матрице изменения структуры . Пусть в старой сети из n ветвей J 1 узлов и одна подсеть, т.е. s 1 = 1 . Тогда, как показано в (1), (2), базисных разомкнутых путей j 1 = J 1 – s 1 , а контуров m 1 = n – j 1 . Если в новой сети также одна подсеть, а число узлов изменилось, например, часть узлов Δ J соединили с другими, и узлов в сети стало меньше, т.е. J 2 = J 1 – Δ J , то уменьшится и число разомкнутых путей:

j 2 = J 2 – s 1 = J 1 – Δ J – s 1 = j 1 – Δ J ,                           (20)

и число замкнутых путей, контуров возрастет:

m 2 = n – j 2 = n – j 1 + Δ J = m 1 + Δ J .                       (21)

Уменьшение числа узлов увеличивает количество независимых контуров и уменьшает количество независимых разомкнутых, и наоборот.

Обозначим вектор базисных путей в старой сети как p¹ α = (^mp¹, ^jp¹) . Пусть часть узлов в ней была замкнута, и независимых контуров стало больше на Δ m = Δ J . Допустим, для наглядности, что новые пути в сети, p² α , состоят из тех же ветвей, что и прежние пути. Тогда в матрицах преобразования старой сети C α `1 <sup>α</sup> и новой сети – C α `2 ^α , все элементы останутся прежними, но строк m -путей будет на Δ m больше, а строк j -путей на Δ m меньше. Новые строки m -путей составят матрицу изменений структуры сети ; обозначим ее как Δ C . Тогда можно выразить C α `2 <sup>α</sup> новой сети через C α `1 ^α старой сети и матрицу изменений Δ C :

n n n m1 mCα`1α m1 mC1 m1 mCα`1α Cα`1α = j1 jCα`1α = j1 jC ;  Cα`2α = Δm ΔCα`α j1 j2 jCα`2α где двойная черта отделяет в матрице Cα`2α подматрицы mC2 и jC2.

m 2	mC 1
	Δ C
	jC 2

Если часть узлов разомкнуть, то их станет больше J 2 = J 1 + Δ J . Разомкнутых путей базиса станет больше на Δ j = Δ J (число подсетей прежнее), а контуров меньше на Δ m = Δ J . Тогда подматрица Δ C в новой сети переходит от ^mC 2 к ^jC 2 , т.е. они меняются местами:

n n m1 Cα`1α = mCα`1α m2 < m1 mCα`1α m2 mC1 ;    Cα`2α =        Δj ΔCα`α =   Δm j2 j1 ΔC j1 jCα`1α j1 jCα`2α jC2 где двойная линия показывает теперь новую границу между mC2 и jC2.

В двойственной сети при этом произойдут обратные изменения, то есть, замкнутся узлы, уменьшится число разомкнутых путей и увеличится число контуров.

Если число замкнутых или разомкнутых базисных путей, при изменении структуры возросло, появилась матрица изменений, то расчет новой сети можно получить по известной матрице решения старой сети и матрице изменений. По решению для сети, где возросло число переменных, можно получить решение для сети, где число переменных уменьшилось, используя инвариант двойственности структуры.

Для пересчета решения старой сети в решение новой сети установим связь между их матрицами решения, Y¹ c и Y² c , и матрицей изменений Δ C . Рассмотрим получение матриц решения, которые обозначим как Y²⁺ c , для базиса замкнутых путей при соединениях узлов, и матриц решения Z^2- c для базиса разомкнутых путей, при разъединениях узлов. Затем получим с использованием инварианта двойственности матрицы решения для обратных задач: при введении разъединения узлов получим матрицу решения Y^{2 –} c , и при введении соединений узлов – матрицу решения Z²⁺ c .

Расчет контурной сети при наложении связей. Матрицы решения старой и новой сети для контуров имеют одинаковый вид, соответственно:

Y¹ c = ^mC 1t (^mC 1 Z ^mC 1t ) ^{– 1 m}C 1 , и Y²⁺ c = ^mC 2t (^mC 2 Z ^mC 2t )^{–1 m}C 2          (23)

где через Y²⁺ c обозначена матрица решения сети при уменьшении числа узлов. Подставим выражение для матрицы ^mC 2 через матрицу ^mC 1 и матрицу Δ C . Произведя преобразования, получим матрицу решения новой сети (для базиса контуров при уменьшении числа узлов), т.е. Y²⁺ c , выраженную через матрицу старой сети Y¹ c и матрицу изменений Δ C :

Y²⁺ c = Y¹ c + Δ Y c = Y¹ c + (I – Y¹ c Z) Δ C t [ Δ C Z (I – Y¹ c Z) Δ C t ]^–1 Δ C (I – Z Y¹ c ),     (24)

где второе слагаемое, обозначенное как Δ Y c , есть матрица изменения решения сети.

Матрицы решения связывают воздействия и отклики в сетях. Например, если заданы ковариантные величины ^md⁰ α , то токи (контравариантные величины ^md c2 ^α ) в новой сети:

^md c2 ^α = Y²⁺ c ^md⁰ α = (Y¹ c + Δ Y c ) ^md⁰ α = ^md c1 ^α + Δ ^md c1 ^α .             (25)

Компоненты вектора Δ ^md c1 ^α обусловлены введением связей, заданных матрицей Δ C . Они изменяют компоненты вектора в старой сети ^md c1 ^α в компоненты новой сети ^md c2 ^α .

Расчеты сетей при разрывании связей. Матрицу решения для замкнутых путей при разрывании связей позволяет получить инвариант двойственности:

Y c ^2– = Y c ¹ – Y c ¹ Δ A t ( Δ A Y c ¹ Δ A t )^–1 Δ A Y c ¹ = Y c ¹ – Δ Z c             (26)

Всего получено 8 формул расчета изменения структуры в двойственных сетях – 4 для заданной сети и 4 – для двойственной сети: по две формулы при наложении связей и две – при разрывании связей. Из каждых двух – одна для замкнутых путей, другая – для

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.) разомкнутых путей. Эти формулы являются основой расчета систем с переменной структурой. Алгоритмы расчета двойственных сетей с переменной структурой позволяют использовать результаты расчета одной конструкции установки для расчета поведения конструкций с изменившимися структурами соединения, состава подсистем.

Сетевые модели для проектирования систем безопасности нефтепереработки

Для применения тензорного метода необходимо создать сетевую модель исследуемой предметной области. Проблема создания сетевых моделей сложных систем состоит в поиске аналогий между величинами сети и предметной области, и структуры, которая адекватно представляет связи между элементами исследуемой системы. Строгих методов создания сетевой модели нет, в каждом случае это, как писал Крон, скорее искусство, чем наука. Тензорный метод двойственных сетей помогает найти аналогии и создать сетевые модели предметных областей; эффективно проводить их расчеты. Преобразования структуры, оставляют инвариантом сумму метрических тензоров двух двойственных сетей .

Аналогии сети и системы . Для создания сетевых моделей устанавливают аналогии между величинами процессов и структуры в сети и в исследуемой предметной области. К изменениям структуры относятся отключение или подключение элементов, изменение соединений элементов, разделение на части или соединение из частей.

Процесс в системе, как поток энергии в виде отклика на воздействие, можно записать простым уравнением поведения [3-5]:

воздействие = сопротивление * отклик.

Заданы воздействие и сопротивление, надо рассчитать отклик. Решение: отклик = воздействие / сопротивление.

Для совокупности элементов установки составляется система уравнений, в которой воздействие и отклик представляют векторы, а сопротивление есть матрица, которую надо обратить; тогда решение принимает вид:

отклик = (сопротивление)^–1 * воздействие.

Величина потока энергии измеряется как произведение воздействия и отклика. Эту величину называют мощность и определяют как энергия в единицу времени:

(поток энергии) = мощность = воздействие * отклик.

Связь воздействия, отклика и метрики (сопротивление материи):

(метрика) = сопротивление = воздействие / отклик.

Величины воздействия и отклика бывают двух типов:

• •    измеряемые в одной точке (например, электрический ток), – продольные величины;

• •    измеряемые как разность значений в двух точках, (например, напряжение, разность потенциалов); – поперечные величины.

Воздействие и отклик, составляющие поток энергии, представлены парой продольной и поперечной величин. Для открытых и закрытых систем они меняются местами. Базисом в открытой системе являются разомкнутые пути, а в закрытой системе – замкнутые пути.

В электрической цепи источники напряжения (поперечная величина) в ветвях цепи – внутренние воздействия. Отклики, токи (продольная величина) возникают в контурах. Расчет контурных токов, по ним – токи и напряжения в ветвях, является решением задачи.

Источники тока (продольная величина) – внешние воздействия, они расположены вне цепи и действуют через узлы входа и выхода. Отклики, напряжения (поперечная величина) возникают в разомкнутых путях. Расчет этих напряжений есть решение задачи.

В каждой предметной области, в том числе в нефтепереработке, произведение продольной и поперечной величин по физической размерности равно мощности (поток энергии, или энергия в единицу времени).

Технология моделирования методом двойственных сетей.

• •    Найти инварианты и привести уравнения поведения исследуемой системы к тензорному виду, т.е. к измеримым величинам.

• •    Установить аналогии между понятиями процессов и структуры данной системы и математической модели – сети.

• •    Рассмотреть простейшую сетевую модель, в которой представлены все процессы и элементы исследуемой системы; выбрать замкнутую или открытую сеть или их комбинацию, чтобы адекватно представить свойства системы.

• •    Построить сетевую модель процессов и структуры реальной системы. Двойственная сеть даст новую информацию о свойствах исследуемой системы.

• •    Расчет откликов на воздействия в сети при изменениях структуры и воздействий на систему, включая аварийные ситуации.

• •    Результаты использовать для расчета, проектирования, управления реальной установки, технической системы, технологического процесса.

Таким образом, метод двойственных сетей обеспечивает расчет изменения процессов при изменении структуры сложных систем. Изучение поведения реальной технической системы при авариях проводится на математической модели.

Тензорным методом автор построил сетевые модели процессов нефтепереработки. В работах [4, 8, 12] материальные и тепловые потоки в установках ректификации представлены контурной и узловой сетью. В контурной сети воздействие задают насосы, откликами являются потоки нефтепродуктов, которые разделяются на фракции и переходят из газовой фазы в жидкую фазу, и обратно. В узловой сети воздействием являются нагрев, теплообмен и охлаждение. Это позволяет разделить фракции. Сетевые модели были разработаны для атмосферной колонны, реакторно-регенераторного блока, установки каталитического крекинга; установки полимеризации.

Результаты применены для прогнозирования пожароопасных ситуаций на объектах нефтепереработки, чтобы оценить изменения процессов при изменении структуры и опасность аварий. Проведены расчеты, например, изменения потоков тепла и массы при отключении элементов установки и дана оценка изменения критичных параметров.

Процесс переработки нефти состоит в разделении исходной смеси на компоненты с различной температурой кипения. Физические процессы разделения смеси состоят в осуществлении испарения или конденсации, за счет чего пар обогащается низкокипящим компонентом (НКК), а жидкость – высококипящим компонентом (ВКК) [2, 4], что дает желаемые составы паровой и жидкой фаз. Для повышения выхода продуктов используется ректификация – процесс разделения жидких смесей на компоненты или их смеси (фракции), при взаимодействии потоков пара и жидкости.

Воздействия: изменения температуры, давления, скорости потока, химические воздействия и т.д. Отклики на воздействия: потоки нефти на входе и потоки конечных продуктов переработки на выходе. Потоки продуктов преобразуются под действием изменения температуры и концентрации. Элементами сети являются ветви, в которых происходит разделение смеси. Подключение или отключение элементов, в зависимости от технологии, или в результате аварий изменяет значения параметров, обладающих свойствами разрушения, например, превышение пределов температуры или давления.

Материальный баланс потоков компонент в колонне определяет узловую подсистему сети, есть аналогии между параметрами массообмена и сети. Воздействиями являются разности концентраций компонента между фазами пара и жидкости. На узловую сеть, потоков материи наложено влияние контурной сети с потоками тепловой энергии.

Тепловой баланс потоков компонент в колонне определяет контурную подсистему сети. Тепловой баланс определяется обменом тепловой энергии между фазами. Для

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.) безопасности важно, чтобы все подведенное в колонну тепло было отведено из колонны парами ректификата, жидким остатком и т.д.

Двойственность понятий сети позволяет представить материальный баланс контурной сетью, а тепловой баланс – узловой сетью. Рассмотрим построение сетевой модели атмосферной колонны первичной переработки нефти и ее применение для анализа потенциально опасных ситуаций, связанных с отключениями частей установки.

Сетевая модель атмосферной ректификационной колонны

Создана сетевая модель одного из блоков первичной переработки нефти, а именно атмосферной ректификационной колонны. В этом блоке нефть разделяется на фракции: бензиновые, керосиновую фракцию, дизельную фракцию и мазут при атмосферном давлении. Основным физическим параметром, представляющим риски аварий, является температура. Для этого применяют нагрев, дистилляцию и ректификацию, конденсацию и охлаждение. Это первичная перегонка, фракции подвергают вторичной переработке.

В колонне основными являются потоки парогазовой смеси нефти на входе, потоки фракций, получаемые на выходе, а также потоки пара. Фракции переходят из газовой фазы в жидкую фазу. Воздействия – изменения температуры, давления, скорости потока и т.д. Отклики – потоки нефти, потоки фракций в жидкой и газообразной фазе. В открытом пути для основного процесса, в контурах циркулярных орошений(ЦО), тепловых потоков, величины воздействия и отклики могут меняться местами. Как источники тока и напряжения в контурах и открытых путях электрической цепи.

Нефть поступает к печам для нагрева и в ректификационную колонну при давлениях, превышающих атмосферное, и при температурах от 3430С до 3710С. Более легкие фракции проникают в верхнюю часть колонны и к другим установкам для дальнейшей переработки.

В ректификационных секциях установок применяется циркуляционное орошение. Отводят циркулирующую флегму двумя тарелками ниже. Колонна К-2 имеет 50 тарелок. Сверху колонны в виде паров выходят газ и легкий бензин, а из внутренних секций – дистилляты лигроина и керосина. Мазут с низа атмосферной колонны направляется в вакуумную печь, где нагревается до 410–4200С и далее поступает в испарительную часть вакуумной колонны.

В целях наиболее полного извлечения нефтепродуктов в нижнюю часть колонны К-2 подается перегретый водяной пар. Печи служат источником нагрева, как сырья, так и пара. На выходах осуществляется отбор фракций: 120-1800С; 150-2500С;. 240-2900С; 290-3500С.

К воздействиям относятся механическое воздействие в виде давления, его создают насосы, нагнетающие потоки; тепловое воздействие создают печи, теплообменники. Охлаждение создают воздушные и водяные холодильники. Отклики. Поток сырья (нефть на входе). Фракции нефти на выходе. Водяной пар – подогрев, отпаривание. Жидкое топливо к печам нагрева. Воздух в воздушных холодильниках. Вода в водяных холодильниках.

Структура установки включает в себя открытые пути и замкнутые контуры. Открытыми путями является движение потока сырья от входа до выхода фракций, к которым относятся – парогазовая смесь наверху К-2, фракции, соответствующие бензинам, керосину, дизельному топливу, мазуту. Контуры: три ЦО, острое орошение, циркуляция пара.

Общая схема колонны К-2 установки с колоннами предварительного испарения К-1, и циркуляционных орошений в колоннах К-6, К-7 и К-9 представлена на рис. 4. В данной сетевой модели колонна К-1 не рассматривается, а колонны К-6, К-7 и К-9 представлены тремя контурами ЦО. Более детальное моделирование повысит размерность задачи. Тогда надо применять тензорный метод для декомпозиции и расчета сетевой модели по частям.

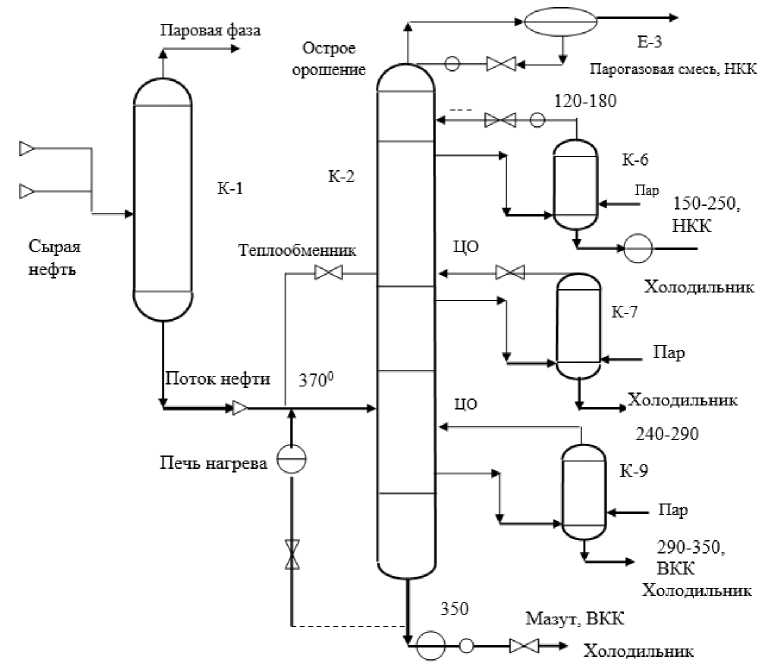
Рис. 4. Схема работы ректификационной колонны установки АВТ. На схеме обозначены: колонна предварительного испарения К1; К2 – ректификационная колонна АВТ; колонна К6; колонна К7; колонна К9; емкость Е3, ЦО – циркуляционное орошение

Следуя технологии тензорного метода, рассмотрим сначала простую установку с минимальным набором элементов, необходимых для процесса ректификации. Для нее установим аналогии и выберем адекватную сетевую модель. Затем применим результаты для расчета сетевой модели, представляющей колонну К-2. Простую реализацию можно представить схемой колонны на рис. 5.а, которой соответствуют сетевые модели из пяти ветвей на рис. 5.б и рис. 5.в. На вход поступает сырье в виде парогазовой смеси. В колонне смесь делится на тяжелую фракцию, уходящую вниз, и смесь легких фракций, которые уходят вверх. Для разделения фракций вводится контур орошения, по которому часть потока охлаждают, а затем подают в колонну, понижая температуру до уровня перехода отделяемой фракции в жидкую фазу, которую выводят здесь. Оставшуюся смесь выводят наверху.

Расчет этих сетевых моделей позволил выбрать вариант, который соответствует реальным потокам продуктов и тепла. С помощью матриц преобразования открытых путей и контуров получены матрицы решения. Потоки массы нефтепродуктов представляют токи отклика на воздействие в виде давления насосов в контурах. Потоки тепла представляют напряжения и токи в узловой сети, как отклики на нагрев и охлаждение.

В результате оказалось, что наилучшие аналогии с атмосферной колонной дает сетевая модель в виде сети с контурами и заземлением.

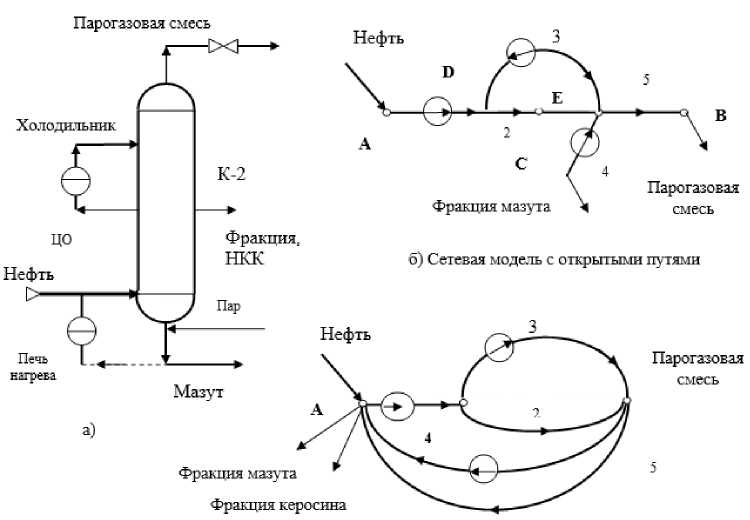
в) Сетевая модель с контурами и заземлением

Рис. 5. Схема простейшей ректификационной колонны и два варианта структуры сетевой модели. а) – ректификационная колонна; б) – сетевая модель с открытыми путями; в) – сетевая модель с контурами и заземлением

Теперь рассмотрим сетевую модель реальной установки, где сырая нефть на входе в процессе ректификации разделяется на четыре фракции, газ и мазут. Также есть поток перегретого пара. Соответствующая сетевая модель представлена на рис. 6.Анализ установки показал, что для создания сетевой модели необходимо не менее 18 ветвей, представляющих от входа до выхода, а также контуры: контур перегретого пара, три циркулярных орошения и острое орошение. Для реальной установки нужно больше ветвей, но данная модель дает наглядное представление матриц.

Чтобы представить все 50 тарелок, колонны, реализующие циркуляционные орошения, теплообменники, нагреватели, в модели необходимо значительно увеличить число компонент. Тензорный метод двойственных сетей позволяет разделить сложную сеть и провести расчет по частям. Это удобно для анализа поведения установки с разной компоновкой блоков, как в интересах проектирования, так и для анализа последствий отключения разных подсистем при аварийных ситуациях.

Сетевая модель соответствует правой части на схеме рис. 4, представляющей основные узлы и агрегаты ректификационной колонны К-2. Сеть включает в себя входной поток нагретой нефти, вывод мазута, фракции 290-3500С. Вместо К-6, К-7, К-9 включены три контура орошения, которые обеспечивают выделение других фракций, а также орошение в верхней части колонны с выводом парогазовой фракции. Отдельно представлена циркуляция пара для отпаривания компонент в нижней части колонны. Узел К – заземление. В него поступает входной поток нефти, из него расходятся разделенные фракции.

Расчет матриц решения для данной модели сделан для контурной сети и узловой сети. Для простоты считаем, «сопротивления» ветвей равны единицам. Далее можно ввести метрику: массу потоков, вязкость, энтальпию, теплоемкость, определяющих сопротивление.

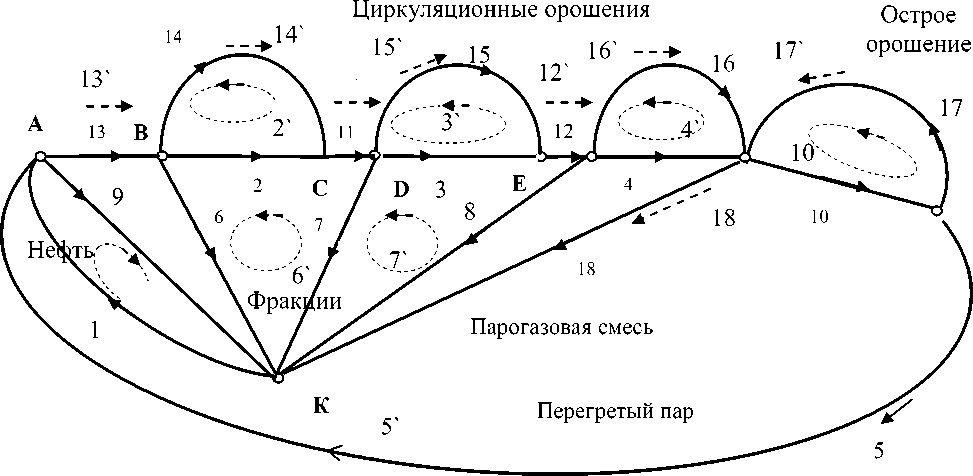
Рис. 6. Сетевая модель колонны К-2 с контурами (три циркуляционных и острое орошение, цикл перегретого пара), и заземлением в узле К

Получив матрицы решения, зададим воздействия и рассчитаем отклики, которые оценим на соответствие реальным значениям потоков материи и потоков тепла. В сети: ветвей n = 18, узлов J = 9, подсетей s = 1, открытых путей j = 9 – 1 = 8, контуров m = 10. Подматрица ^mС контурной сети состоит из строк 1-10; для путей на рис. 6 она имеет вид:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1	1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	m
2	0	1	0	0	0	0	0	0	0	0	0	0	0	-1	0	0	0	0	m
3	0	0	1	0	0	0	0	0	0	0	0	0	0	0	-1	0	0	0	m
4	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	-1	0	0	m
5	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	0	m
6	0	-1	0	0	0	1	-1	0	0	0	-1	0	0	0	0	0	0	0	m
7	0	0	-1	0	0	0	1	-1	0	0	0	-1	0	0	0	0	0	0	m
8	0	0	0	-1	-1	0	0	1	-1	-1	0	0	0	0	0	0	0	0	m
9	0	0	0	0	1	0	0	0	1	1	0	0	0	0	0	0	0	-1	m
10	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	m

Матрица решения контурной сети Y c = ^mC a^a t ( m C a'^a Z ae ^mC e^e t ) " ^{1 m}C a'^a имеет вид:

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1     2793	111	-6	-132	-648	567	234	252	1356	-324	222	-12	789	111	-6	-132	324	384
2      111	2454	129	72	102	-435	501	114	-111	51	759	258	324	-1695	129	72	-51	42
3         -6	129	2460	183	144	-126	-513	405	6	72	258	771	132	129	-1689	183	-72	222
4     -132	72	183	2643	402	-6	-222	-771	132	201	144	366	138	72	183	-1506	-201	735
5      -648	102	144	402	1722	222	-84	-516	648	861	204	288	426	102	144	402	-861	-918
6      567	-435	-126	-6	222	2226	-618	-240	-567	111	-870	-252	1356	-435	-126	-6	-111	-234
7     234	501	-513	-222	-84	-618	2028	-582	-234	-42	1002	-1026	384	501	-513	-222	42	-360
8     252	114	405	-771	-516	-240	-582	2352	-252	-258	228	810	-12	114	405	-771	258	-1026
9     1356	-111	6	132	648	-567	-234	-252	2793	324	-222	12	-789	-111	6	132	-324	-384
10     -324	51	72	201	861	111	-42	-258	324	2505	102	144	213	51	72	201	1644	-459
11      222	759	258	144	204	-870	1002	228	-222	102	1518	516	648	759	258	144	-102	84    1/4149
12      -12	258	771	366	288	-252	-1026	810	12	144	516	1542	264	258	771	366	-144	444
13      789	324	132	138	426	1356	384	-12	-789	213	648	264	2004	324	132	138	-213	-150
14      111	-1695	129	72	102	-435	501	114	-111	51	759	258	324	2454	129	72	-51	42
15        -6	129	-1689	183	144	-126	-513	405	6	72	258	771	132	129	2460	183	-72	222
16     -132	72	183	-1506	402	-6	-222	-771	132	201	144	366	138	72	183	2643	-201	735
17      324	-51	-72	-201	-861	-111	42	258	-324	1644	-102	-144	-213	-51	-72	-201	2505	459
18      384	42	222	735	-918	-234	-360	-1026	-384	-459	84	444	-150	42	222	735	459	2388

В сетевой модели внутренними воздействиями являются источники ЭДС, а в реальной системе, например, насосы, создающие давление. В сетевой модели откликами являются контурные токи, токи и напряжения на отдельных ветвях, а в реальной системе – потоки нефти и ее продуктов (жидкие, газовые, парогазовые). Умножение матрицы решения на источник воздействия, вектор ЭДС в а дает отклики в ветвях, токи 1 ^в _с.

Пусть источники ЭДС заданы вектором в а =

1     2     3     4     5     6     7     8     9    10    11    12    13    14    15    16    17    18

150

15

10

14

52

20

25

25

10

10

1

1

1

10

8

12

-6

16

Умножив Y c на e α , получим токи i ^α c и напряжения e α ^c в ветвях связанной сети.

1      2     3     4     5      6      7     8      9    10     11     12     13    14    15    16    17    18

102,1

13,1

6,4

4,1

0,9

23,9

10,5

4,5

57,9

2,5

21,2

10,7

45,1

8,1

4,4

2,1

1,5

5,3

Эти значения представлены на рис. 7. Отклики удовлетворяют законам Кирхгофа, что является проверкой правильности расчетов.

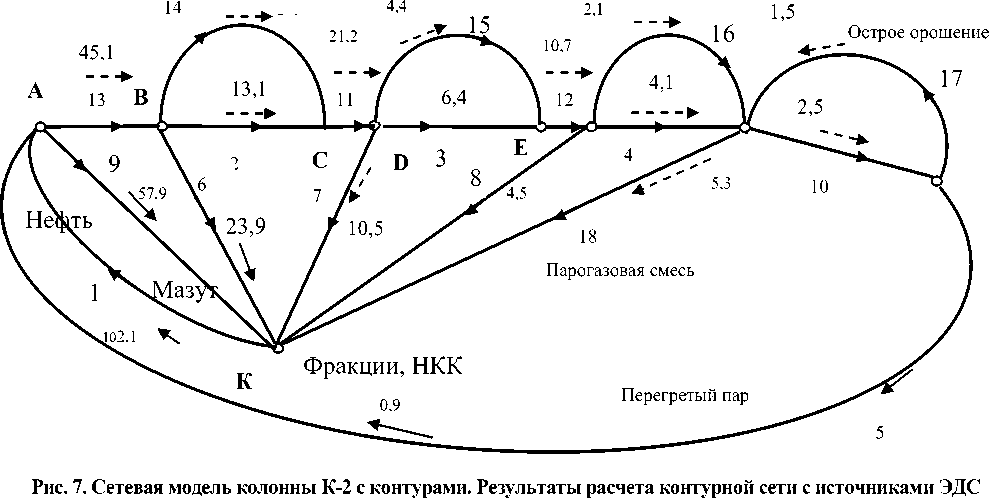
Можно видеть, что по ветви 1 поступает поток исходного сырья, который разделяется на поток мазута в ветви 9 и остальные фракции в ветви 13 вместе с потоком пара из ветви 5. Далее из парогазовой смеси отделяется фракция ВКК по ветви 6. Оставшийся поток проходит три ЦО, в результате выделяются три фракции НКК, включая бензин и газ после острого орошения. В узле К , который рассматривается как заземление, сохраняется баланс входного потока и выходных потоков, каждый из которых выводится по своему пути.

Полученный результат в пропорциях соответствует распределению потоков нефтепродуктов в реальной колонне. При надлежащей настройке сетевую модель можно применять для анализа процессов ректификации.

Проведем расчет узловой сети с данной структурой, и оценим, как источники тепла создают потоки на ветвях. Воздействия здесь источники тока, а отклики – напряжения на ветвях. Проводимости ветвей считаем равными единицам. Их можно ввести как энтальпии, при переходе из жидкой фазы в газообразную фазу.

Матрица А узловой сети ортогональна к С контурной сети А = C¹ t . Для расчета используется подматрица открытых путей матрицы А , которые играют здесь роль базиса. Выполнив вычисления, получим Z c = ^jA ^a a t (A ^a a Y ^ae -A/ P t )"¹ jA pP . Эту матрицу легко получить из инварианта двойственности – сумма матриц решения контурной и узловой сети равна единичной матрице. Введя вектор тепловых воздействий (нагрев и охлаждение), умножив на него матрицу решения Z _c , получим отклики. Здесь нагрев в печи отнесен к ветви входа 1, а охлаждение – во всех ЦО, остром орошении, и на выходах фракций. Значения откликов удовлетворяют законам Кирхгофа в узлах и по контурам. В ветвях 1 (печь на пути входного потока) и 5 (контур подачи в низ колонны перегретого пара), где происходит нагрев, потоки совпадают с направлением ветви, а в остальных, где идет охлаждение, противоположны. Результат соответствует потокам тепла в реальной колонне.

Выполнив вычисления по формуле Z c = ^jA ^a a t (A ^a a Y ^{ae j}A pP t )"^{1 j}A pP , получим

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1      1356	-111	6	132	648	-567	-234	-252	-1356	324	-222	12	-789	-111	6	132	-324	-384
2     -111	1695	-129	-72	-102	435	-501	-114	111	-51	-759	-258	-324	1695	-129	-72	51	-42
3         6	-129	1689	-183	-144	126	513	-405	-6	-72	-258	-771	-132	-129	1689	-183	72	-222
4      132	-72	-183	1506	-402	6	222	771	-132	-201	-144	-366	-138	-72	-183	1506	201	-735
5      648	-102	-144	-402	2427	-222	84	516	-648	-861	-204	-288	-426	-102	-144	-402	861	918
6     -567	435	126	6	-222	1923	618	240	567	-111	870	252	-1356	435	126	6	111	234
7     -234	-501	513	222	84	618	2121	582	234	42	-1002	1026	-384	-501	513	222	-42	360
8     -252	-114	-405	771	516	240	582	1797	252	258	-228	-810	12	-114	-405	771	-258	1026
9    -1356	111	-6	-132	-648	567	234	252	1356	-324	222	-12	789	111	-6	-132	324	384
10      324	-51	-72	-201	-861	-111	42	258	-324	1644	-102	-144	-213	-51	-72	-201	-1644	459    1/4149
11     -222	-759	-258	-144	-204	870	-1002	-228	222	-102	2631	-516	-648	-759	-258	-144	102	-84
12       12	-258	-771	-366	-288	252	1026	-810	-12	-144	-516	2607	-264	-258	-771	-366	144	-444
13     -789	-324	-132	-138	-426	-1356	-384	12	789	-213	-648	-264	2145	-324	-132	-138	213	150
14     -111	1695	-129	-72	-102	435	-501	-114	111	-51	-759	-258	-324	1695	-129	-72	51	-42
15         6	-129	1689	-183	-144	126	513	-405	-6	-72	-258	-771	-132	-129	1689	-183	72	-222
16      132	-72	-183	1506	-402	6	222	771	-132	-201	-144	-366	-138	-72	-183	1506	201	-735

17	-324	51	72	201	861	111	-42	-258	324	-1644	102	144	213	51	72	201	1644	-459
18	-384	-42	-222	-735	918	234	360	1026	384	459	-84	-444	150	-42	-222	-735	-459	1761

Инвариант двойственности выполняется – сумма матриц решения контурной сети и узловой сети равна единичной матрице. Если введем теперь вектор тепловых воздействий (нагрев и охлаждение), и умножим на него матрицу решения, то получим отклики. Здесь нагрев в печи отнесен к ветви входа 1, а охлаждение – во всех ЦО, остром орошении, и на выходах фракций.

Рассмотрим поведение установки при изменениях структуры, связанных с возможными авариями. Пусть в структуре сетевой модели разорваны (разрушены) два контура – острое орошение, где ветвь 17 оторвана от узла H, и вывод газовой фракции, где ветвь 18 оторвана от узла F, как показано на рис. 8. Тогда в матрицах преобразования С и А произойдут изменения – два контура, соответственно 9 и 10 превратятся в разомкнутые пути. В матрице для расчета контурной сети ^mС станет на две строки меньше, а в матрице для расчета узловой сети ^jА станет на две строки больше. Алгоритмы расчета не меняются. Снова рассчитаем контурную и узловую сеть, получим матрицы решения. Используя прежние воздействия, получим отклики, и сравним их с откликами для заданной структуры установки.

В сети ветвей n = 18, узлов J = 11, подсетей s = 1, открытых путей j = 10, контуров m = 8. Два пути стали открытыми, размерность подпространства контуров уменьшилась на два, размерность подпространства открытых путей возросла на два. В матрице ^m С последние два столбца 17 и 18 становятся нулевыми. Матрица решения Y c1 представлена фрагментом:

	1	2	3	4	5	14		15	16	17	18
1	907	37	-10	-72	-144		37	-10	-72	0	0
2	37	822	41	17	34		-569	41	17	0	0
3	-10	41	816	33	66		41	-575	33	0	0
4	-72	17	33	794	197		17	33	-597	0	0
5	-144	34	66	197	394		34	66	197	0	0

14	37	-569	41	17	34		822	41	17	0	0	1/1391
15	-10	41	-575	33	66		41	816	33	0	0
16	-72	17	33	-597	197		17	33	794	0	0
17	0	0	0	0	0		0	0	0	0	0
18	0	0	0	0	0		0	0	0	0	0

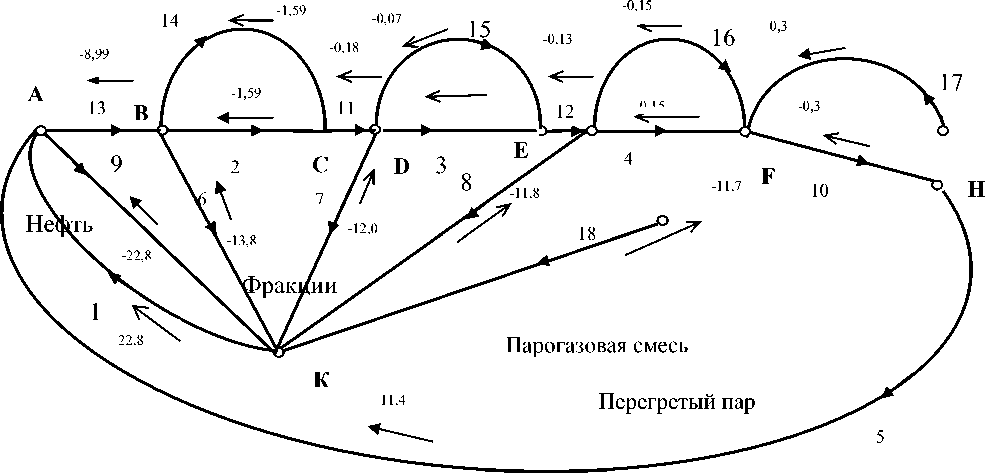
Рис. 8. Сетевая модель колонны К-2 с отрывами ветви 17 от узла Н и ветви 18 от узла F.

Соответственно, контуры 7 и 8 в матрице преобразования стали разомкнутыми путями

Воздействиями являются источники ЭДС, а в реальной системе, например, насосы, создающие давление. Откликами являются контурные токи, токи и напряжения на отдельных ветвях, а в реальной системе – потоки нефти и ее продуктов (жидкие, газовые, парогазовые). Полученную матрицу умножим на вектор воздействия e α , чтобы получить отклики, токи i ^β с .

Возьмем прежний вектор e α , умножим на него Y c1 – получим отклики, токи i ^α c 1 = e α ^c 1 .

1      2     3     4     5      6      7     8      9    10     11     12     13    14    15    16    17    18

101,2

13,0

5,9

2,6

3,1

24,4

11,3

6,6

58,8

3,1

21,1

9,8

45,4

8,0

3,9

0,6

0

0

Сравним результаты со значениями потоков в установке, работающей в штатном режиме, iαc которые даны выше. Разность между ними, и накопления отклонений за разные

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.) промежутки времени представлены в таблице для момента отключения элементов, а в следующих столбцах – накопление избытков массы через 5, 10 и 20 единиц времени.

Динамика роста опасности пожара при разрушении

Номера ветвей	Воздействия	Отклики, штатные	Отклики при аварии	Накопление избытка массы, в единицах времени
				1	5	10	20
1	150	102,1	101,2	-0,9	-4,68	-9,37	-18,74
2	15	13,1	13,0	0,1	0,35	0,69	1,38
3	10	6,4	5,9	0,5	2,58	5,16	10,33
4	14	4,1	2,6	1,5	7,69	15,39	30,77
5	52	0,9	3,1	-2,2	-11,11	-22,23	-44,46
6	20	23,9	24,4	-0,5	-2,44	-4,87	-9,75
7	25	10,5	11,3	-0,8	-3,97	-7,95	-15,90
8	25	4,5	6,6	-2,1	-10,72	-21,44	-42,88
9	10	57,9	58,8	-0,9	-4,68	-9,37	-18,74
10	10	2,5	3,1	-0,6	-3,11	-6,23	-12,46
11	1	21,2	21,1	0,1	0,69	1,38	2,76
12	1	10,7	9,8	0,9	4,66	9,33	18,66
13	1	45,1	45,4	-0,3	-1,75	-3,49	-6,99
14	10	8,1	8,0	0,1	0,35	0,69	1,38
15	8	4,4	3,9	0,5	2,58	5,16	10,33
16	12	2,1	0,6	1,5	7,69	15,39	30,77
17	-6	1,5	0,0	1,5	0,0	0,0	0,0
18	16	5,3	0,0	5,3	0,0	0,0	0,0

Разница между значениями потоков для штатного режима и аварийного режима была рассчитана для «мгновенных» значений, т.е. потоков в единицу времени. Полученная

Электронное научное издание

«Международный электронный журнал. Устойчивое развитие: наука и практика»                                                             вып. 2 (13), 2014, ст. 2

Выпуск подготовлен по итогам IV Международной научной конференции по фундаментальным и прикладным проблемам устойчивого развития в системе «природа – общество – человек»: наука, инженерия, образование (22 декабря 2014 г.) разность будет накапливаться, и можно рассчитать время, за которое накопленные избыточные массы создадут аварийную ситуацию.

В ветвях 4, 12, 16 происходит накопление избыточной массы, в сравнении с обычными значениями, это наиболее аварийно опасные участки. Для разных изменений в конструкции необходимо составить «банк данных» вариантов разрушений и реакции на них.

Для реальных задач объем вычислений растет. Для ускорения расчетов применяются алгоритмы тензорного метода расчета по частям. Ранее полученное решение преобразуется в новое решение с помощью матрицы преобразования измененных путей. Их можно применять для анализа поведения системы, состоящей из установок, соединенных в единый технологический комплекс. Например, нефтеперерабатывающий завод в целом.

Алгоритм расчета матрицы решения замкнутых путей при разрывании связей в контурной сети, по формуле (27). Она описывает изменения в заданной сети при разрывании связей – для замкнутых путей и обеспечивает расчет при разрывании в структуре сети, которое задано ортогональной матрицей Δ A , в отличие от соединений. Знак «минус» показывает, что метрические параметры сети для замкнутых путей уменьшаются при разъединении части узлов, что уменьшает число контуров.

Рассмотрим применение данного алгоритма для структурных изменений, отключения ветвей 17 и 18. При разрыве двух узлов два контура превратились в открытые пути. В соответствии с формулой расчета изменения матрицы решения старой сети в матрицу решения аварийной установки, нужна матрица измененных путей в двойственной сети Δ A . Матрица решения старой сети, Y c ¹, получена выше. Матрица изменений – это две строки 9 и 10 матрицы А для тех путей, которые из контуров превратились в открытые пути, т.е. Δ A =

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
9	-1	0	0	0	0	1	1	1	1	0	0	0	0	0	0	0	0	0
10	0	0	0	0	-1	0	0	0	0	1	0	0	0	0	0	0	0	0

Вычисляя матрицу решения сети с разрывами, получим матрицу в скобках Δ A Y c ¹ Δ A t порядка 2х2, обращение которой требует меньше вычислений, чем матрицы 10х10:

	9	10	9		10
9	0,575555	-0,11062	( Δ A Y c 1 Δ A t )–1=    9	1,800863	0,329937
10	-0,11062	0,60376	10	0,329937	1,716735

Умножив ее справа и слева на Y c ¹ Δ A t и Δ A Y c ¹ , получим матрицу изменений, т.е. Δ Z c .

Вычитая ее из Y c ¹ : Y c ^2– = Y c ¹ – Δ Z c , получим матрицу решения аварийной сети.