Закономерности движения водного потока при движении плота в условиях продленной навигации
Автор: Корпачев В.П., Злобин А.А., Корпачев И.В.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Техника
Статья в выпуске: 10, 2012 года.
Бесплатный доступ
В статье рассмотрены основные закономерности движения водного потока при движении плота в условиях продленной навигации. Исследовано влияние на скорость стесненного потока таких параметров, как шероховатость льда, ширина канала в ледовом поле и шероховатость русла.
Сплав леса, продленная навигация, шероховатость льда, сжатый поток, скорость потока
Короткий адрес: https://sciup.org/14082065
IDR: 14082065 | УДК: 627.224.8
Текст научной статьи Закономерности движения водного потока при движении плота в условиях продленной навигации
В связи с этим возникает необходимость аналитического и экспериментального исследования закономерностей движения водного потока, стесненного ледяным покровом при наличии в нем канала. При транспортировке плотов в ледовом канале необходимо учитывать дополнительное сопротивление воды от стеснения потока и ледового сопротивления.
Цель исследований . Определить формулу скорости потока в стесненном сечении с учетом влияния ледяного покрова при наличии в нем канала. Исследовать влияние на скорость стесненного потока таких параметров, как шероховатость льда, ширина канала в ледовом поле и шероховатость русла.
Результаты исследований и их обсуждение . Выведем уравнение движения потока под ледяным покровом при наличии в нем канала [3] . Для вывода уравнения выделим сечениями 1-1 и 2-2 участок потока с уклоном i > 0, площадью живого сечения ω и длиной l . Обозначим через P 1 и Р 2 давление в центрах тяжести живых сечений (рис. 1).
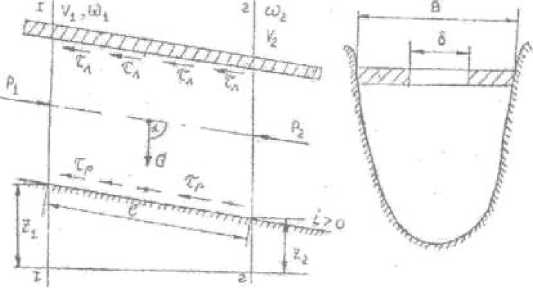
Рис. 1. Расчетная схема для вывода уравнения движения потока под ледяным покровом
Силы гидродинамического давления в сечениях 1-1, 2-2
F 1 = P 1 ω 1 , F 2 = – Р 2 ω 2 .
Сила F 2 направлена против направления движения, поэтому имеет знак минус.
Сила трения потока о стенки русла
Тр = τрχрl ,(2)
где τ р – удельная сила трения потока о стенки русла, зависит от шероховатости русла;
χ р – смоченный периметр русла.
Сила трения потока о нижнюю поверхность ледяного покрова
Тл = τлχлl ,(3)
где τ л – удельная сила трения потока о нижнюю поверхность ледяного покрова;
χ л – смоченный периметр ледяного покрова.
Сила тяжести отсека
G = ρgωl .(4)
Спроектируем действующие силы на ось движения потока
F1 – F2 + G cosα – Тр -ТЛ = 0.(5)
Подставив значение действующих сил в уравнение (5) и разделив все члены уравнения на ρgω , по- лучим
Р 1 pg
—
p 2
—+ zi pg
—
_ *p Xp i , tл Xл i z2 =--1-- pg^ pgu
.
Запишем уравнение Бернулли для сечений 1-1 и 2-2
P i «14 Р2 а 21-4
— +--- + z 1 = — +---
pg pg
pg pg
+ Z 2 + hw ,
где
h w – потери напора при движении потока на участке 1.
Так как ω1 = ω2 = ω и принимая α1 = α2, уравнение (7) примет вид где
P 1 pg
—
Р 2
--+ z-i_ — Z 2 = h w . pg
Сопоставляя уравнения (6) и (7), получим
* р X p l * л X4 ,
+--= h, pgu pgu
' W .
Введем в уравнение (6) значение гидравлического уклона
* р X р + * л X л = { pgw pgw ,
ω/χ л = R л – гидравлический радиус смоченного периметра ледяного покрова; ω/χ р = R р – гидравлический радиус смоченного периметра русла.
С учетом значений R л , R р уравнение (10) запишется
* P pgR p
tn
+ -4- = i pgR л
R„ или, введя отношение а = — ., получим ’ " R р ' J
Tq ^л
-+ + - л = IR„. ард рд
При условии развитого турбулентного движения можно предположить, что суммарные силы трения пропорциональны квадрату скорости движения потока при наличии ледяного покрова, то есть
- р- + — = К v Л , ард рд
где К – коэффициент пропорциональности;
υ л – скорость движения потока при наличии ледяного покрова и канала в нем.
Из уравнений (12) и (13) следует
IR л = К v Л ,
откуда
v л
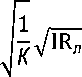
= с л VIR л ,
где через с л обозначили коэффициент Шези для потока с ледяным покровом и наличием в нем канала.
Определим скорость движения потока для широкого прямоугольного русла при наличии канала во льду шириной b. Так как ω = ВН и χ л = 2(В+Н) – b, то гидравлический радиус при наличии канала во льду равен
Ш ВН
R = — =-----------.
л X л 2(В + Н) -Ь
Представим R л в безразмерной форме, введя относительную глубину m = Н/В и относительную ширину прорези канала m' =b/В . С учетом m и m' получим
mB
R=
2(1 + т) —т
.
Коэффициент Шези в формуле (15) может быть определен по формуле [1]
1 1
c
пР = п Н 6 n пр
c р
(1 + а 1'5 )2/ з ,
где с р – скоростной коэффициент свободного ото льда потока;
п пр – приведенный коэффициент шероховатости для потока под ледяным покровом.
На основе сопоставления результатов расчета с данными натурных наблюдений рекомендуется применять формулу Н. Н. Павловского для определения n пр [3]
n пр =
n л χл + n р χр χ л + χ р
В формуле (18) а = П л /П р ., где П л - коэффициент шероховатости ледяного покрова; П р - коэффициент шероховатости русла.
Для рек в бытовом состоянии Н. Н. Белоконь [1] рекомендует принимать значения коэффициента шероховатости ледяного покрова, приведенные в таблице 1.
Значения коэффициента шероховатости ледяного покрова
Таблица 1
|
Период ледостава |
Расчетное значение |
|
Первые 10 дней ледостава |
0,150–0,050 |
|
10–20-й день после ледостава |
0,100–0,040 |
|
20–60-й день после ледостава |
0,050–0,030 |
|
60–80-й день после ледостава |
0,040–0,015 |
|
80–110-й день после ледостава |
0,025–0,010 |
Примечание. Верхние пределы указанных значений должны применяться в расчетах при образовании торосистого льда или шуги; нижние – на участках с гладким льдом.
Подставляя значение гидравлического радиуса R л и коэффициента Шези С л в формулу (15), получим скорость движения потока при наличии канала во льду
А л =
Ср
(1 + а 1, 5)2 /з
ImB
\ 2(1 + m) — m ‘
или
1 ImB
Ал = —H /6 . (21)
П пр 2(1 + m) — m
Введем следующие обозначения (рис. 2):
ω, υ – площадь поперечного сечения потока, средняя скорость его течения, не стесненного судном;
-
ω с , υ с – площадь поперечного сечения потока, средняя скорость его течения, когда в нем находится судно с площадью миделевого сечения ¤;
-
h, h c – глубина потока соответственно в нестесненной его части перед носовой частью судна и в мидели.
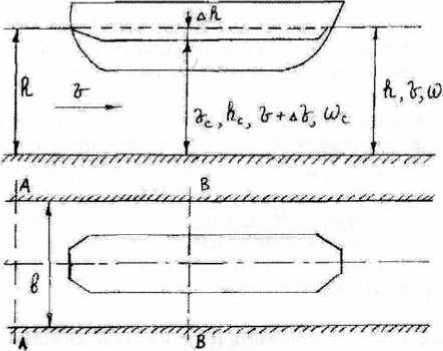
Рис. 2. Схема движения судна в ограниченных условиях
При движении плота на участках, ограниченных по ширине и глубине, в районе движения судна наблюдается понижение уровня. Для определения величины понижения уровня воды в районе нахождения плота воспользуемся принципом подвижных координат, соединенных с судном [3] . В зоне расположения судна, вследствие уменьшения площади живого сечения потока поперечным сечением корпуса судна, скорость течения увеличивается на некоторую величину Δ υ . Скорость в стесненном сечении потока υ с = υ + Δ υ .
Для определения скорости υ с воспользуемся уравнением Бернулли, записанным для сечений АА и ВВ
U2
h + ;f = (h — Ah) + z~-2g2g
Для определения υ с необходимо установить величину понижения уровня воды Δh в сечении ВВ.
Величина Δ υ может быть приближенно определена из уравнения неразрывности
υω = (υ+Δυ)ωс.(23)
Площадь потока, стесненного судном, определится выражением
ωс = ω – ¤ – bΔh,(24)
где ¤ – площадь погруженной части корпуса судна по мидельшпангоуту;
-
b – средняя ширина канала, вычисляемая по выражению b=ω/h.
Считая произведение Δhb малым по сравнению с площадью ω, им можно пренебречь. Тогда, подставляя (24) в (23) и решая относительно Δυ, получим
¤ 1
JV = V„ . = %,,
где n=ω/¤ – профильный коэффициент.
Зная значение Δυ, можно определить теоретическую величину понижения уровня воды Δh , воспользовавшись для этого уравнением (22). Подставляя в уравнение (22) значение υ с = υ + Δ υ и решая относительно Δh, получим
Ah = 1 fv + ^Jv.
g2
Подставляя значение Δυ (25) в формулу (26), получим
Ah =
U 2 n — 0,5 g (n — 1)2.
Для практических расчетов для определения величины Δh рекомендуется формула, учитывающая не только изменение формы поперечного сечения, но и характер обтекания корпуса судна [3]
Δ h =
— K2
(—)2| r, n 2g
где К 2 = 1 — . 1 .
Vn-4,2
Значение скорости потока в стесненном сечении с учетом величины Δh получим из уравнения (22)
V с = V,2 К fn n ' .
Значение скорости потока в стесненном сечении с учетом влияния ледяного покрова при наличии в нем канала получим, подставив в уравнение (29) υл г 1 1/ f ImB 2 /n -1 2
u C = —H /б 2 - К 2 (. I . (30)
П пр 2(1+ m) - m n
Исследуя выведенную формулу (30), можно определить, как влияют на скорость потока υ лс такие показатели, как b, n л , n р . Сравним значения средней скорости потока υ, вычисленной по формуле Шези (31), со значениями скорости потока в стесненном сечении в условиях продленной навигации υ лс .
u = C VRI
В качестве постоянных параметров примем средние показатели для Ангаро-Енисейского региона: LxBxT – габаритные размеры плота, соответственно длина, ширина и осадка, 500х22х0,75 м; B р – ширина русла реки, 400 м; Н – глубина потока, 1,5 м.
Результаты расчетов влияния n л на υ лс представлены в таблице 2 и на рисунке 3.
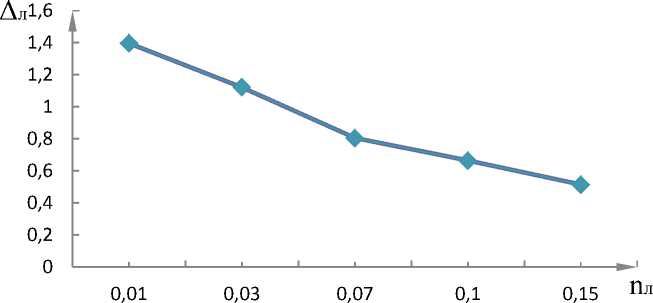
Рис. 3. Влияние шероховатости льда на скорость потока в условиях продленной навигации
Расчет влияния n л на υ лс
Таблица 2
|
№ п/п |
n л |
χ л , м 2 |
n пр |
m' |
υ, м/с |
υ л , м/с |
υ лс , м/с |
△ л (П л ) = 1 -^ |
|
1 |
0,01 |
366 |
0,04 |
0,085 |
0,65 |
0,77 |
0,89 |
1,40 |
|
2 |
0,03 |
0,05 |
0,62 |
0,71 |
1,12 |
|||
|
3 |
0,07 |
0,07 |
0,44 |
0,51 |
0,80 |
|||
|
4 |
0,1 |
0,08 |
0,37 |
0,42 |
0,66 |
|||
|
5 |
0,15 |
0,11 |
0,28 |
0,33 |
0,51 |
При изменении шероховатости льда от 0,01 до 0,15 скорость стесненного потока уменьшается на 36,4 %.
Результаты расчетов влияния b на υ лс представлены в таблице 3 и на рисунке 4.
Таблица 3
Расчет влияния b на υ лс
|
№ п/п |
B, м |
χ л , м 2 |
n пр |
m' |
υ, м/с |
υ л , м/с |
υ лс , м/с |
△ л (П л ) = 1 -^ |
|
1 |
26 |
374 |
0,07 |
0,07 |
0,65 |
0,44 |
0,51 |
0,800 |
|
2 |
30 |
370 |
0,07 |
0,08 |
0,44 |
0,51 |
0,803 |
|
|
3 |
34 |
366 |
0,07 |
0,09 |
0,44 |
0,51 |
0,805 |
|
|
4 |
38 |
362 |
0,07 |
0,10 |
0,44 |
0,51 |
0,807 |
|
|
5 |
42 |
358 |
0,07 |
0,11 |
0,45 |
0,51 |
0,809 |
Δ 0,81 0,808 0,806 0,804 0,802 0,8
0,798 0,796
0,794

—I_____________I_____________I_____________I_____________I_____________I_____________I_____________I_____________I________^J
26 30 34 38 42 b, м
Рис. 4. Влияние ширины канала на скорость потока в условиях продленной навигации
При изменении ширины канала в ледовом поле от 26 до 42 м при ширине плота 22 м скорость сжатого потока увеличится на 1,12 %.
Результаты расчетов влияния n р на υ лс представлены в таблице 4 и на рисунке 5.
Расчет влияния n р на υ лс
Таблица 4
|
№ п/п |
n р |
n пр |
m' |
υ, м/с |
υ л , м/с |
υ лс , м/с |
△ (n л ) = 1 -^ |
|
1 |
0,025 |
0,05 |
0,085 |
1,65 |
0,64 |
0,74 |
0,45 |
|
2 |
0,045 |
0,06 |
0,91 |
0,52 |
0,60 |
0,66 |
|
|
3 |
0,065 |
0,07 |
0,64 |
0,44 |
0,51 |
0,80 |
|
|
4 |
0,085 |
0,08 |
0,49 |
0,38 |
0,44 |
0,91 |
|
|
5 |
0,105 |
0,09 |
0,39 |
0,34 |
0,39 |
0,99 |
Δ л 1,2
0,8
0,6
0,4
0,2

______________I_________________________________I_________________________________I_________________________________I_________________________________I_________________________________I_________________________________I_________________________________I_________________________________I________________
0,025 0,045 0,065 0,085 0,105
n р
Рис. 5. Влияние шероховатости русла на скорость потока в условиях продленной навигации
При изменении шероховатости русла от 0,025 до 0,105 скорость сжатого потока увеличится в два раза.
Выводы. Основное влияние на изменение скорости потока в условиях продленной навигации оказывают шероховатость льда и шероховатость русла. Полученные расчетные данные и зависимости могут быть
использованы при определении сопротивления воды движению лесотранспортных единиц и судов в условиях продленной навигации


