Закономерности механического поведения зернистых композитов, связанные с формой и размерами элементов структуры

Актуальность развития новых математических моделей и мето-ДОВ, учитывающих неоднородность полей напряжений и деформаций в структурных элементах, а также многостадийность процессов микро-и макроразрушения, связаны с необходимостью получения новых дан-ных о влиянии параметров структуры на неупругое механическое по-ведение и эффективные деформационные и прочностные свойства структурно неоднородных сред. В данной работе в качестве структур-но неоднородных сред рассматриваются зернистые композиты.

Одной из особенностей неупругого поведения материалов явля-ется закритическая стадия деформирования. Вопросы теоретического и экспериментального изучения закономерностей закритического де-формирования материалов привлекают внимание исследователей в связи с необходимостью использования деформационных резервов материалов, повышения несущей способности и живучести конструк-ций [1‒4]. Развитие методов расчета ответственных конструкций с оценкой живучести и безопасности требует получения информации о закономерностях механического поведения композиционных мате-риалов на стадии закритического деформирования [5, 6].

Определенные закономерности могут быть обнаружены в резуль-тате вычислительных экспериментов . В частности, ранее было показа-но , что накопление повреждений носит многостадийный характер , проявляют себя зависимость ниспадающего участка диаграммы от ви-да напряженного состояния и «квантовый» характер структурного раз-рушения, определенное соотношение свойств структурных элементов приводит к самоподдерживаемому разрушению, при котором закрити-ческая стадия деформирования даже при «жестком» (кинематическом) нагружении очень ограниченна [7, 8].

Для выявления связей структурных параметров с закономерно-стями неупругого деформирования авторами ранее был предложен оригинальный алгоритм синтеза микроструктур зернистых композитов [9], который имитирует пошаговый рост эллипсоидов (в плоском слу -чае ‒ эллипсов). На рис . 1и2 показаны модели микроструктур из 100 зерен с разными коэффициентами формы k_f a/b и относительных размеров k r a max / a min соответственно ^, где a и b ‒ большая и малая полуоси эллипсоидов; a _max и a _min ‒ размеры больших полуосей наи ^-большего и наименьшего эллипсоидов.

Макроразрушению структурно-неоднородных тел предшествует сложный процесс потери несущей способности элементов структуры, сопровождаемый перераспределением напряжений и деформаций. В результате равновесный процесс накопления повреждений может перерасти в лавинообразный и в итоге привести к образованию макро-трещины. Изучение кинетики этого процесса важно для выявления факторов появления макроскопической трещины и исследования осо-бенностей механического поведения структурно-неоднородных сред.

а                       б                              в

Рис. 1. Модели зернистых структур с коэффициентами размера kr = 2 и формы:

(a) kf =1; (б) kf = 2 ; (в) kf =5

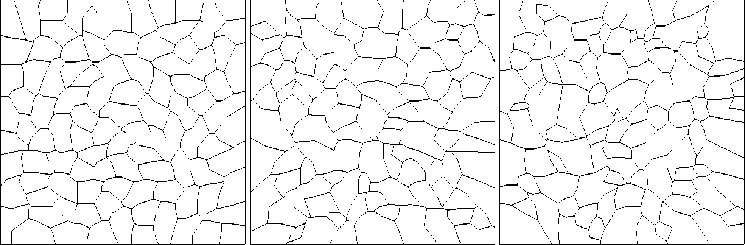
а                       б                      в

Рис. 2. Модели зернистых сред с коэффициентом формы kf- =2 и с заданным по равномерному закону коэффициентом размера: (a) kr =1; (б) kr = 2; (в) kr =3

В работе используются модели разрушения по совокупности кри-териев прочности, которые позволяют различать механизмы разрушения структурных элементов [1]. Для случая изотропного материала учитываются два различных вида разрушения (отрыв и сдвиг). Рассмотренные критерии разрушения представляются в виде неравенств

, j где jn - независимые инварианты тензора деформаций, вид и число ко-n торых соответствует типу анизотропии материала [10], j С - прочностные константы материала; fm - некоторые универсальные функции.

Для описания процессов неупругого деформирования и разруше-ния структурно-неоднородных сред используется двухуровневая структурно-феноменологическая модель механики композитов [11]. Вычисление полей напряжений оу(r) и деформаций £j(r) в элементах структуры осуществляется при помощи замкнутой системы урав-нений, в которую входят уравнения равновесия, записанные без учета массовых сил, геометрические соотношения Коши и определяющие соотношения для структурных элементов:

ГУ - • ij , j

(r )=0,

s    =2 ujjWuj, i(r) ], ij (r) _ Cijkl(r) I^lkinn — ^kinn (^, js cr )^ ^nn (r) , / \           *

11. ( Fl ,   = P .. F .

uiv/L  jrj ’ где Cijkl - компоненты тензора упругих модулей, Ikinn^Wto + +6kn5in )/2 - компоненты единичного тензора, 5kn - символ Кронекера , ^kinn - компоненты тензора поврежденное™ четвертого ранга, Еи - границы тела, на которых заданы условия макрооднородной деформации si,.

Для изотропных материалов определяющие соотношения пред -ставляются в следующем виде:

ijA ^г )=(3 ^(r )0- k ) D jnn+ 2 G^ 0" g)^ jnn )s nn( r ), (6) где K и G - модули объемного сжатия и сдвига соответственно, Dijnn ^{1 3}M nn ^и H ....I ....D .... . Тензор поврежденности четвертого ранга в этом случае определяется двумя независимыми матери -альными функциями k и g . При моделировании упругохрупкого поведения значения указанных функций скачкообразным образом изменя-ются от 0 до 1 при выполнении критериев разрушения.

Напряжённо-деформированное состояние макрообъёмов характеризуется тензорами макронапряжений gj^ и макродеформаций *jy, определяемыми осреднением по объёму соответствующих величин на структурном уровне . Связь между макронапряжениями и макродефор-мациями определяет эффективные свойства зернистых структурно-неоднородных сред и может быть охарактеризована при помощи рас-четных диаграмм деформирования.

Численное моделирование механического поведения зернистых структурно-неоднородных сред осуществлялось с использованием раз-работанного программного комплекса, в основе которого заложены метод конечных элементов, процедура метода переменных параметров упругости и автоматического выбора шага нагружения [12], ведущего к регистрации разрушения минимально возможного числа элементов в каждой итерации [13].

Синтезированные зернистые структуры разбиваются на тре-угольные конечные элементы, причем на каждое зерно приходится в среднем по 50 элементов дискретизации. Разработанный программный комплекс численного решения краевых задач механики неупругого деформирования и разрушения позволяет при фиксированном уровне нагружения получать картины неоднородных полей напряжений и де-формаций. На рис . 3 показаны иллюстрации неоднородных полей в элементах структуры компонент тензора напряжений о11, О 22 , Т12 "     2 )

и второго инварианта тензора напряжении j' при отсутствии разру-шенных конечных элементов и заданных по равномерному закону в интервале упругих свойств зерен.

„                „                                   ~2 )

При этом второй инвариант тензора напряжении j ■ определяет-:

2 \       /'—- ^3' j□ (r         ij ij , ° ij     ij 3 о kk ij ,(7)

где 5 ij ‒ символ Кронекера. Для структур, представленных на рис. 1, проведено численное моделирование процессов структурного разру-шения в условиях одноосного деформирования. Считается, что зёрна представленных микроструктур изотропны и однородны. Модули упру-гости зёрен E_i задаются по равномерному закону в интервале 0,8 E_sr E_i 1, 2 E sr , где E_sr = 100 МПа . Коэффициент Пуассона для всех зёрен принимается равным 0,3. При этом прочностные характеристики зёрен задавались по двухпараметрическому закону распределения Вей-

2 ) \ булла co средним значением прочностных свойств ( j cr = 10 МПа и коэффициентом вариации kV = 0,5                   :

kV

,

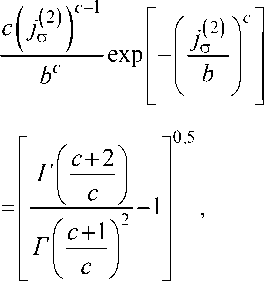
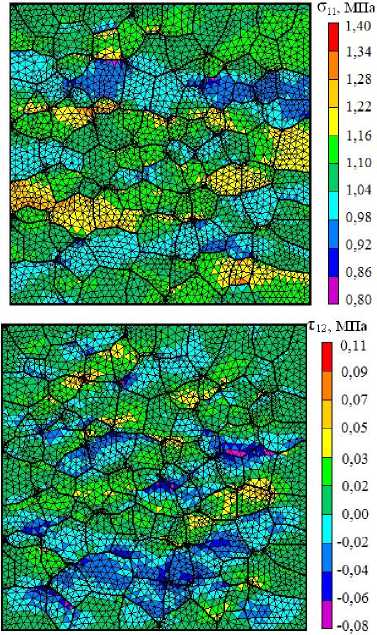
Рис. 3. Неоднородные поля компонент и второго инварианта тензора напряжений в элементах структуры в условиях одноосного деформирования

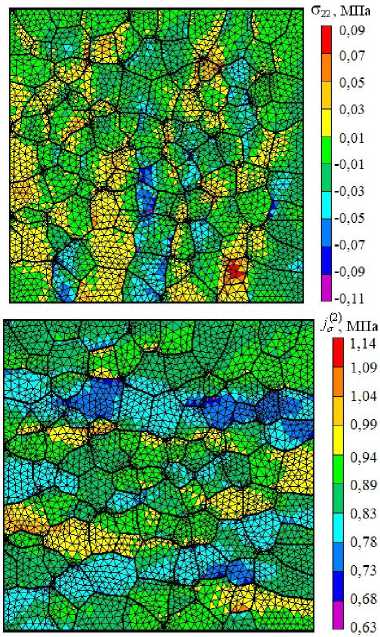
где bиc ‒ соответственно параметры масштаба и формы плотности J 2 Л          , распределения f j□ I;Г( )‒ гамма-функция.

На рис. 4 приведены полученные зависимости компоненты тен-зора макронапряжений о11 от компоненты тензора макродеформаций s11, отражающие влияние формы структурных элементов на механиче -ское поведение области деформирования. На рис. 5 показаны картины дефектных структур для зернистых композитов с различным коэффи-циентом формы при фиксированном уровне нагружения.

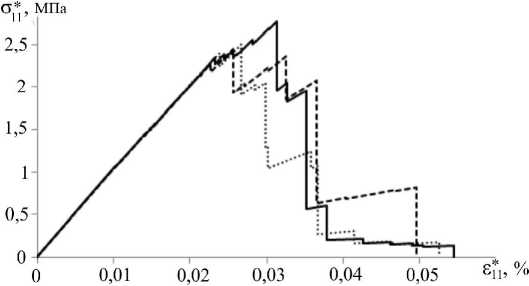
Рис. 4. Диаграммы деформирования при одноосном «жестком» нагружении зернистых структур с коэффициентом формы k_f , равным 1 (сплошная линия), 2 (штриховая линия)и5 (пунктирная линия)

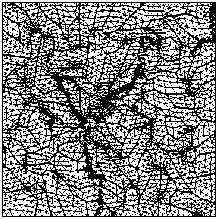
Рис. 5. Иллюстрации дефектных структур для зернистых композитов с разным коэффициентом формы зерен: ( а ) k_f 1; ( б ) k_f 2; ( в ) k_f 5

Видно, что наличие в структурах большого числа зёрен с вытяну-той формой приводит к снижению прочностных характеристик. Это связано с тем, что вытянутая форма зёрен даёт более сильную концен-трацию напряжений в области деформирования, которая тем больше оказывает влияние на процесс структурного разрушения, чем больше задан разброс модулей упругости зёрен.

Проведен анализ закономерностей неупругого деформирования и разрушения зернистых структурно-неоднородных сред с различным относительным размером зёрен, вид микроструктур которых приведен на рис. 2. Были выбраны следующие параметры структуры: -ция задана по равномерному закону в интервале от 0 до 180° С; коэф-фициент формы зерен k_f 2; коэффициент относительных размеров зерен принимал значения k_r 1, 2 и 3.

Для представленных структур проведено численное моделирова-ние процессов структурного разрушения в условиях одноосного де-формирования . При этом прочностные и упругие характеристики зёрен задаются аналогичным образом с предыдущей задачей. На рис . 6 при-ведены полученные зависимости компоненты тензора напряжений о11 от компоненты тензора деформаций s11, отражающие влияние разме-ров структурных элементов на механическое поведение области де-формирования .

Из рис. 6 видно, что у расчетных диаграмм деформирования с большим коэффициентом относительных размеров выше предельное значение о11 max и^, следовательно ^, выше прочностные характеристики ^. Однако у диаграммы деформирования зернистой структурно-неоднородной среды с k_r 1 наблюдается более протяженный участок закритического деформирования, что свидетельствует о лучшей спо-собности материала сопротивляться разрушению .

На рис. 7 представлена зависимость объемной доли поврежден-ности оо материала от величины деформации при одноосном пропор-циональном деформировании для рассматриваемых зернистых струк-тур . При этом величина поврежденности оо при решении плоской зада-чи для зернистых структурно-неоднородных сред соответствует отношению площади разрушенных конечных элементов к общей пло-щади области деформирования.

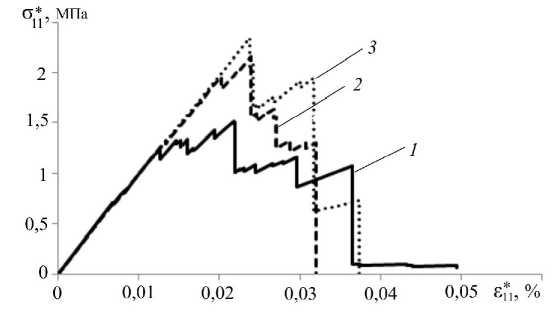
Рис. 6. Диаграммы деформирования при одноосном «жестком» нагружении зернистых структур с коэффициентом размера: (a) kr =1 (сплошная линия); (б) kr =2 (штриховая линия); (в) kr =3 (пунктирная)

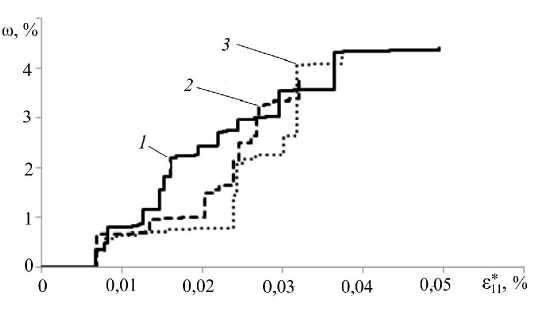
Рис. 7. Зависимость объемной доли повреждённости от величины деформации при одноосном «жестком» нагружении зернистых структур, с коэффициентом размера: (a) kr =1 (сплошная линия); (б) kr = 2 (штриховая линия); (в) kr =3 (пунктирная)

Таким образом, для выявления связи параметров структуры с закономерностями неупругого деформирования и разрушения зернистых структурно-неоднородных сред разработан комплекс программ, включающий в себя программу синтеза зернистых микроструктур и про -грамму для численного моделирования процессов неупругого дефор -мирования и структурного разрушения. Определены закономерности механического поведения зернистых структурно-неоднородных сред, связанные с формой и относительными размерами элементов структу-ры при случайных значениях упругих и прочностных характеристик зерен.