Закономерности передачи нагрузки от волокон к матрице в случае неидеального контакта

Введение. Краевые эффекты, связанные с перераспределением нагрузки между компонентами, играют важную роль в микромеханике композитных материалов и конструкций [1-6]. Протяженность зоны краевого эффекта невелика и, как правило, находится в пределах одного-двух характерных размеров элементов структуры композита. Однако именно в этой зоне возникают наибольшие локальные напряжения, которые могут приводить к развитию дефектов на микроуровне.

Рис. 1. Схема нагружения

Рис. 2. Расчетная модель

В настоящей работе рассматривается задача о продольном растяжении (сжатии) фрагмента однонаправленного композита, состоящего из упругой матрицы О^ и бесконечно длинных цилиндрических линейно упругих волокон О^2^ с постоянным радиусом а (рис. 1). Будем считать, что к поперечному сечению z = 0 каждого волокна в на- правлении образующей приложена нагрузка интенсивностью о0. Выделим в рассматриваемом сечении ячейку периодичности и, в первом приближении, заменим ее внешнюю границу окружностью радиуса R (рис. 2). Используемая расчетная схема аналогична полидисперсной модели [7], которая дает хорошие результаты для эффективных упругих модулей трансверсально-изотропных композитов при малых и средних объемных наполнениях c(2) = (a/R )2 . Среди моделей сред с регулярной структурой наиболее близкие свойства проявляет композит с гексагональным размещением волокон.

Краевая задача. Будем считать, что компоненты тензора деформаций в точках, принадлежащих матрице, удовлетворяют геометрическим соотношениям Коши:

( 1 )_S u r ^{1 )}     ( 1 )_ « 2

ьr =      , Ье =     , о r          r

_е(1)_ 3 и^ m 5 ц М d u W (1)_ (1)

ьz = д , ьrz = д  + д   , ьrе = ьеz = 0, оz          оz    о r

(1)( где ur v, uz — перемещения в радиальном и продольном направлениях, а компоненты тензора напряжений - уравнениям равновесия с отсутствующими массовыми силами:

a (1)  U1)^1)  д^1)        л^1)  дЛ1)U

‘°- + о r   °е +°grz. = о, '°- +°Нт^      = о.(1)

0 r r 0z         0z    0 rr

Здесь и далее верхние индексы ( i ), i = 1, 2, 3, обозначают матрицу (область Q^{( 1 )} ), волокна (область Q ( ² ) ) и межфазную границу 0О .

Определяющие соотношения:

о« = 2 K «[ ( 1 -^MfW

„ (1) _ 2^(1) Г h - Л о(1) + „(О) + ,/0)1 ое =2KT (1 ^ )ье +^ ьr +Ц ьz , а<4= 2KT'» [(1 -цМ)Ег + ц<1)Е!') + Ц<1)ее1)],

„ (1)__г,№,(1)     _п(1)__п(1)_₀     ^(1 )_ G ^{( 1 )}

о rz = G ^ь rz ,    о r е = ^ е ₂ = 0, K T =       /_П

1 - 2ц()

содержат модуль сдвига G ^{( 1 )} и коэффициент Пуассона ц^{( 1 )} матрицы.

Будем предполагать, что внешняя граница ячейки свободна от напряжений:

о

r

=°,, °$ | г = R

= °.

г=R

Для моделирования эффекта неидеального контакта примем ги-

потезу о том, что касательные напряжения о Zz

= а (3)|

„ zz г=a I

на меж- z = a

фазной границе 5Q пропорциональны скачку продольных перемеще

ний

[ и®

u Z9

= Аuz3):

г=a

og ' = ^А U ^{( 3 )} ,                       (3)

b где G(3) - модуль сдвига материала межфазного слоя, а b - его толщина.

В рассматриваемом случае нарушение связи между компонентами проявляется в проскальзывании волокна относительно матрицы. В то же время в радиальном направлении условия контакта на границе раздела фаз остаются идеальными:

„"1    =_ср ', u ^l   = ^.

= a                  I z = a

Предложенная модель справедлива в случае слабого поперечного взаимодействия компонентов, характерного для большинства волокнистых композитов при продольной деформации.

Введем параметр связи а (° < а <  1):

G (3) = 1 -а bG(1)    а a и положим bja ^ °. В асимптотическом пределе а = ° соответствует идеальному контакту (А и(3) = °), а = 1 - полному отсутствию контакта между волокнами и матрицей (oZ3) = °), а промежуточные значения ° < а < 1 описывают случай неидеального контакта.

Еще одно упрощающее предположение заключается в том, что для высокомодульных волокон можно пренебречь поперечными деформациями:

и * ‘> I      = ° .                                       (4)

= a

Данная гипотеза используется во многих работах [2, 4] и позволяет рассматривать волокно как одномерный объект.

Уравнение равновесия для волокна запишем в виде d 0?

dz

+ f0 (z) + fl (z ) = 0,

где ^^{2 )} = E ^{( 2 )} du Z ²⁾ dz - продольное напряжение, E ^{( 2 )} - модуль Юнга;

fo (z) = ^о5(z) - приложенная к волокну объемная сила; 5(z) - дельтафункция Дирака; f (z) = £ ^ZadбД лa2) = 20^.3/a - объемная сила, связанная с перераспределением напряжений между волокном и матрицей.

Аналитическое решение. Компоненты вектора перемещений и тензора напряжений в матрице удобно выразить через упругий потенциал Лява W [8]:

u? = "! 2 W- , u ? = 2 ( 1 -Ц^{( 1 )} ) V ² W -0 W ,         (6)

0 r 0 z             ^х '         0 z

■ m = 2G(1)-°f p(1)V2W -°W) , o^ 2G(1)-° p(1)V2W -1 °W , r         0z(            0r2 )      6         0z\           r 0r)

o^ 2GW-0^ 2 -p(1)) V2W ^W , z          0z L^         '          0z2 J

a(l) = 2G :| 1 L : V2W-02W . 0 r Lx        ’          0z J

Тогда уравнения равновесия (1) удовлетворяются тождественно, а условия совместности деформаций сводятся к бигармоническому урав нению

V2V2W = 0.

Применим к соотношениям (2)-(7) преобразование Фурье f ( 5 )=J f ( z ) exp ( - isz ) dz. Тогда в пространстве изображений получим следующие зависимости для компонент вектора перемещений:

u r ⁱ⁾ = - is ° W , u z ^i} = 2 ( 1 -p^{( 1 )} ) V ² W + s ² W , 0 r

- (2)_   1 /   ^2 -(3)^

u^z "  5 ² E (<^{0 +} a ° ^{rz )}

и тензора напряжений:

- ( ¹ ) о rz

-^{( 1 )}    _0Л,(1). f (1)^ ²

оr = 2G()is | a( )V W

( ¹ ) о z

^^^^^^^^

5 2W

5 r ².

■ j, о е ^{1 )} = 2 G ^{( 1 )} is ( a^{( 1 )}V 2 W

= 2 G^s Г ( 2 a , VW ₊ sW\

= 2G [ (1 ^Ч

V W + s 2W

~ ( 2 ) , о z

• V ( 2 )”( 2 ) -( 3 ) = isE^v ui_z , о rz

, о rz

^^^^н

1 W

5 r ) ’

r

r = a

_- (1)

= о rz

, r=a

а также граничные условия

- ( ¹ ) о rr

r = R

~ ( 3 ) о rz

= 0,

- ( ¹ ) о rz

= 0, r=R

~ ( 1 ) u r

r = a

= 0,

= G(1) 1 -g r=a a g

Г- ( 1 ) u z

^^^^^^^^

- (2)1 u z

r = a

и уравнение для упругого потенциала:

V V W = 0.

Решение уравнения (11) имеет вид

W = Ci( s) Iо ( s| r) + C2 ( s) srIi ( sr) + Cз ( s) Kо ( sr) + +C4(s) sK( sr), где 10, 11 и K0, K1 — модифицированные функции Бесселя первого и второго рода соответственно. Функции C1 (s), C2 (s), C3 (s) и C4 ( s) находятся из граничных условий (10).

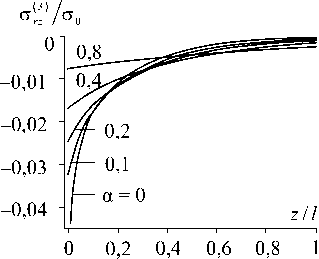
Рис. 3. Касательные напряжения на межфазной границе

^о Z ²7^о 0

–0,46

–0,47

–0,48

–0,49

–0,5

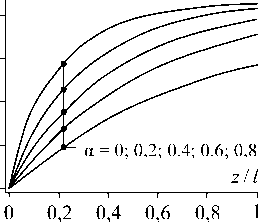
Рис. 4. Продольные напряжения в волокне

Окончательное решение строится путем обращения изображений (8), (9) по формуле да

f (z)=2я J f (z) exp (isz) ds

-да

В работе выполнялось численное интегрирование с использованием пакета Maple.

Численные результаты. Для иллюстрации полученного решения рассмотрим однонаправленный композит на основе эпоксидной матрицы ( G ^{1 1 1} = 1,53 ГПа и р^ = 0,33), армированной стеклянными волокнами ( E ( ^{2 )} = 69 ГПа). На рис. 3 и 4 представлены зависимости напряжений 0 . 3 , а ^, от безразмерной продольной координаты z[l ( l - расстояние между центрами соседних волокон, а z = 2 R ). Расчеты были выполнены для объемного наполнения стекловолокном c ^{( 2 )} = 0,4.

В случае идеального контакта ( а = 0 ) наличие сосредоточенной нагрузки в точке z = 0 приводит к сингулярности решения. Имеют место следующие пределы:

|°2!| >да,   |^h^0   при z^0,

I ^ 1

^ 0,

I ^|

, 0₀ c ^{( 2 )} E ^{( 2 )}

2 E 0

при z > да ,

где E ₀ « ( 1 - c ^{( 2 )} ) E ^{( 1 )} + c ^{( 2 )} E ^{( 2 )}

- эффективный модуль Юнга в направ лении   армирования,   определенный по правилу   смеси,

и E (1) = 2G(1)( 1 + ц^).

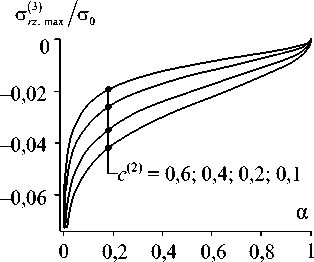
Рис. 5. Максимальные касательные напряжения при z = 0

На рис. 5 проиллюстрирована зависимость g^ max от параметра а. Как видим, ослабление связи между волокнами и матрицей снимает сингулярность и позволяет ограничить максимальные напряжения ^С Г ) шах ^{= С} Г ^| о на границе раздела 5Q . При этом обеспечивается более равномерное перераспределение нагрузки, а также увеличивается протяженность зоны краевого эффекта.