Закономерности процесса разрушения отходов лесозаготовок

На современном этапе развития лесного комплекса остро встает вопрос о необходимости широкого использования комплексной переработки сырья [6], ресурсосберегающей техники [7], малоотходных и энергосберегающих технологий, вовлечения в производство новых видов сырья и материалов. В связи с возможным появлением принципиально новых материалов на основе длинноволокнистых фракций древесины и соответствующих технологий представляет интерес исследовать деление древесины отходов лесозаготовок на технологические фрагменты безножевыми способами [2]: сжатием и ударом, а также сам процесс деструкции древесины при поперечном нагружении в малоизученной области, так как имеются предпосылки для практического использования деструктурированной древесины в качестве исходного компонента при разработке принципиально новых материалов.

Важное значение на разрушение древесины имеют три составляющих древесного вещества, придающие древесине свойства твердого тела, образованного из клеточных оболочек; воды,

находящейся как в клеточных оболочках [4], так и в полостях клеток и сосудов; воздуха, занимающего свободные от воды внутренние полости древесины.

Эти составляющие имеют различную сопротивляемость действию сжимающей нагрузки. Древесное вещество и вода практически несжимаемы. Воздух, содержащийся в древесине, при наличии свободной воды находится в виде пузырьков (эффект Жамена) и является упругим сжимаемым телом. Сжатие воздуха значительно больше, чем древесного вещества и воды, поэтому можно считать, что изменение объема древесины при воздействии объемной деформирующей нагрузки возможно только за счет сжатия паровоздушной смеси.

В случае когда клетки древесины заполнены водой полностью, деформация древесины за счет сжатия клеток и сосудов становится невозможной. Поэтому сближение сжимающих поверхностей будет возможно только за счет сдвигов структурных элементов относительно друг друга, что и требуется для эффективного безножевого измельчения древесины объемно деформирующей нагрузкой, приложенной в направлении, перпендикулярном волокнам.

Древесина деформируется в результате изменения расстояний между мицеллами. С увеличением влажности древесины сила взаимного притяжения между мицеллами уменьшается, часть пектиновых веществ и гемецеллюлоз, входящих в состав клеточных оболочек (и межклеточного вещества) и склеивающих мицеллы и фибрилы между собой, переходит в раствор, что будет способствовать снижению коэффициента внутреннего трения древесины.

В случае прогрева древесины во влажной среде повышается ее деформативность. При увлажнении древесины происходит перерождение пластической деформации в упругую. Это перерождение протекает особенно интенсивно при одновременном прогреве и увлажнении.

При разработке модели процесса разрушения под действием сжимающей нагрузки отходов лесозаготовок поперек волокон [ 3 ] (в нашем случае – образцов, выпиленных из ветвей и сучьев), необходимо сделать некоторые допущения:

• 1.    Процесс разрушения носит многостадийный характер.

• 2.    Образцы однородны по своей структуре и обладают трансверсальной изотропией.

• 3.    Зависимости между напряжениями и деформациями имеют линейный характер до момента возникновения трещины (хрупкое разрушение), показанные обобщенным законом Гука.

• 4.    До момента разрушения образец испытывает плоское напряженное состояние.

• 5.    Будем считать, что условием локального разрушения тела (страгивание трещины) является равенство коэффициента интенсивности напряжений К_I его критическому значению К_IC .

• 6.    Идеализированные образцы имеют форму ^. цилиндра с радиусом окружности в поперечном сечении, равным среднему радиусу образца в его поперечном сечении.

Нами предложена модель многостадийного разрушения, идеализированная диаграмма которой представлена на рис. 1.

О1

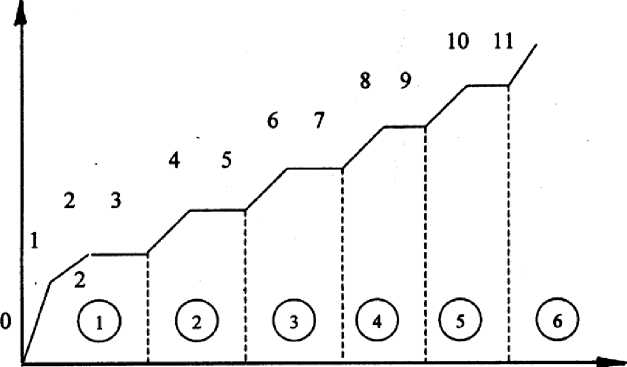
Рис. 1. Идеализированная диаграмма многостадийного процесса разрушения

Обозначения точек соответствуют следующим явлениям:

Точка 1 – момент возникновения трещины;

Точка 2 – момент полного раскрытия трещины;

Точка 3 – момент, когда заканчивается переориентация частиц.

В дальнейшем эти точки последовательно повторяются.

Участки 0–1, 1–2, 2–3 соответствуют первым трем стадиям разрушения, из которых состоит первый цикл (цифра 1 в кружке). Далее стадии последовательно повторяются, составляя последующие циклы разрушения.

Первая стадия длится от начала приложения нагрузки к образцу до момента возникновения первой трещины. Зависимость между напряжениями и деформациями на данной стадии (исходя из сделанных допущений) можно описать, используя математический аппарат теории упругости.

Для определения напряжений в произвольной точке М воспользуемся решением аналогичной задачи в теории упругости [1]. Круглая пластина (форма поперечного сечения образца близка к окружности с диаметром d ), толщина которой равна единице, сжимается двумя силами Р, направленными по ее диаметру О₁О₂ (рис. 2).

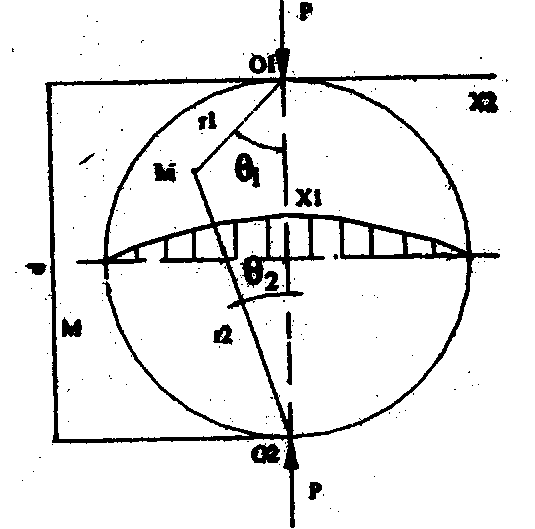
Рис. 2. Схема приложения нагрузки к образцу и эпюра растягивающих напряжений (первая стадия)

Формулы для определения напряжений в произвольной точке М, полярные координаты которой относительно диаметра О₁О₂ составляют значения углов Q₁ и Q₂ и радиусов r₁ и r₂ , выглядят следующим образом:

^σ 11

2P⎜⎛cos3Q1-cos3Q2-1 π ⎝ r1        r2

σ 22

τ ₁₂

• 2P I sin «.Q+.Q

π ⎝      r1                r2

2 P _⎜ ⎛ sin Q 1 cos² Q 1 π ⎝       r ₁

sin Q2 cos2 Q2

+J r2

Анализируя вышеприведенные формулы, необходимо отметить, что максимальные значения нормальных растягивающих напряжений принимают по направлению диаметра O₁ О₂ (см. рис. 2), то есть первичная трещина возникнет в этом сечении.

Необходимо также отметить, что в данном направлении (растяжение поперек волокон) древесина обладает наименьшей прочностью.

После определения напряжений в произвольной точке осуществляем пересчет полученных напряжений к главным по следующим формулам:

° 1 = ^0,5 ° ⁺ О 22

^{) +   (} °_п  ° 22 ) + 4 ^г 12

) - V (ои - °22 )2 + 4Г;2,

° 2 = ^{0,5 (} О 11 + О 22

где σ₁₁ , σ₂₂ – напряжение в произвольной точке М; r₁ , r₂ – радиусы произвольной точки М.

Появлению трещины благоприятствуют следующие моменты:

– наличие сердцевинных лучей (разрыв слабых клеток сердцевинного луча в поперечном направлении);

– наличие в данном сечении такого элемента строения древесины, как сердцевина, обладающая рыхлой структурой и являющаяся наименее прочным элементом строения древесины.

При разной температуре прочность изменяется в зависимости от влажности. Связь между температурой и прочностью древесины выражается формулой:

σ = – at +b, (3) где a, b – постоянные от пород и вида напряжений; t – температура.

Таким образом, для перехода остаточной деформации в упругую необходима влага; нагрев древесины при наличии значительного количества связанной влаги в ней является своеобразным катализатором этого процесса.

Вторая стадия длится от момента возникновения трещины (рис. 3) до момента потери целостности образца или до момента полного раскрытия трещины. Эпюра напряжений в зависимости от расстояния приведена на рис. 3.

Здесь необходимо отметить роль первичного дефекта. За такой дефект в древесине ветвей и сучьев можно принять элемент их строения – сердцевину.

При математическом описании данной стадии применяем методы механики разрушения [5].

Для распространения трещины отрыва необходимо, чтобы выполнялось условие К_I ≥ К_IC (коэффициент интенсивности напряжений K₁ был больше или равен его критическому значению К_IC ).

Данные по коэффициенту интенсивности напряжений KI применительно к отходам лесозаготовок (ветвям и сучьям) в справочной литературе и литературных источниках нам не встречались, поэтому определяем их экспериментальным путем.

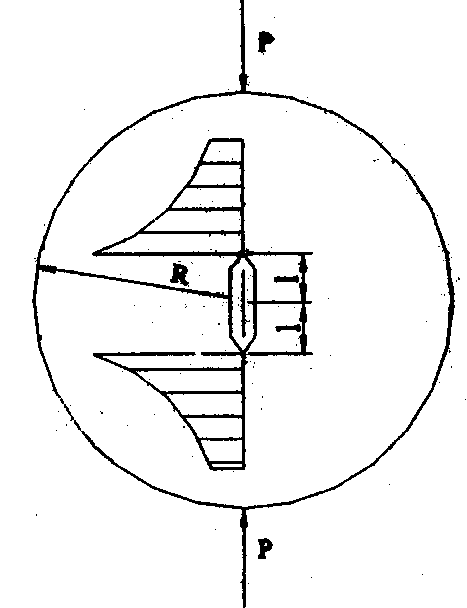
Рис. 3. Схема образца с центральной трещиной на сжатие вдоль диаметра (вторая стадия)

При экспериментальном определении критического коэффициента интенсивности напряжений требуется определить критическое напряжение, при котором начинается лавинообразный рост трещины, также необходимо узнать длину начальной трещины.

Зная критическое растягивающее напряжение и длину трещины, критический коэффициент интенсивности напряжений можно определить по следующей формуле:

K IC = Y ( L ) ^aV ''n , ⁽⁴⁾

где Y( L ) – функция, зависящая от геометрической формы образца и длины трещины; σ ₁ ⁽²⁾ – действующее напряжение растяжения в точке 2 (см. рис. 1), которое раскрывает трещину; l – длина (полудлина) трещины.

При математическом описании модели на второй стадии необходимо знать и относительную деформацию, при которой произойдет полное раскрытие трещины. Эти данные также требуют экспериментального определения.

В конце второй стадии образуются два сегмента, которые начинают воспринимать сжимающую нагрузку. Разрушение этих сегментов будет происходить также от максимальных растягивающих напряжений.

Нормальные напряжения можно рассчитать методом конечных элементов.

Третья стадия длится от момента полного раскрытия первоначальной трещины до момента восприятия нагрузки частицами, переориентировавшимися за это время. Для этой стадии характерно постоянство напряжения, то есть увеличивается только деформация. В качестве моделей, описывающих разрушение образца на третьей стадии первого цикла, нами предложены идеализированные модели, учитывающие геометрические параметры образца.

Для первой модели будем считать, что в момент окончания переориентации частиц они примут форму прямоугольника (рис. 4) с шириной b , равной радиусу первоначального образца, то есть получим две частицы шириной b , равной радиусу R первоначального образца. При этом полагаем, что сумма площадей данных прямоугольников равна площади поперечного сечения идеализированного образца, то есть площади окружности с радиусом R.

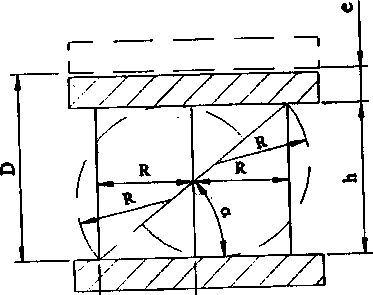
b

Рис. 4. Частицы, получаем ые н а третьей стадии (первая модель)

Для того чтобы определить абсолютную деформацию е , необходимо найти высоту прямоугольников h , исходя из равенства площадей:

h =----= 1,571 R .               (5)

2R

Получаем, что абсолютная деформация в конце третьей стадии равна разности высоты прямоугольника h и диаметра D. Относительная деформация будет равна отношению абсолютной деформации к диаметру и с учетом предыдущей формулы составит:

h-D

ε отн = ^h _D ^D =- 0,215.          (6)

Знак «–» в этой формуле означает, что относительная деформация является деформацией сжатия.

Также нами предложена еще одна идеализированная модель, но в ней частицы после разрушения принимают форму, близкую к окружности, и их площади поперечного сечения будут равны половине первоначальной площади поперечного сечения образца.

В процессе проведения лабораторных экспериментов исследовали влияние исходных характеристик образца на прочность древесины сучьев и ветвей (при их разрушении). Проводили исследования размерных характеристик получаемых частиц после межволоконного разделения.

При планировании экспериментов для математического описания процесса разрушения образцов (сучьев и ветвей) было принято, что значение функций отклика описывается с достаточной точностью полиномами не выше второго порядка.

При проведении эксперимента по разрушению образцов проводилась видеосъемка. Из анализа материалов видеосъемки с большой долей вероятности можно сделать вывод о том, что разрушение образцов происходит от растягивающих напряжений.

Сделанные допущения в теоретическом обосновании подтверждаются на опыте, то есть первоначальная трещина возникает в сердцевине образца от воздействия нормальных растягивающих напряжений (отрыв).

В системе Statistika был сделан расчет множественной регрессии для определения зависимости растягивающего напряжения от переменных факторов (диаметр, длина, влажность). Уравнения регрессии выражаются следующим образом (для натуральных факторов):

σ ₁⁽¹⁾ = 0,287319 + 0,045517D +0,021667L +

+ 0,00667D² + 0,000151W² – 0,001100DL – (7)

– 0, 001171DW– 0,000312LW + 0,000017DLW .

σ₁⁽²⁾ = – 7,77348 + 0,53286D + 0,30263L –

– 0,00139L² + 0,00053W² – 0,00855DL – (8)

– 0,00620DW – 0,00137LW + 0,00010DLW, где σ1(1) – растягивающее напряжение в момент возникновения трещины; σ1 (2) – растягивающее напряжение в момент разрушения образца (потери целостности).

Анализ уравнений регрессии показывает, что растягивающие напряжения в момент возникновения трещины и в момент разрушения образца значительно зависят от влажности.

Результаты статистического анализа относительных деформаций, характеризующих процесс разрушения образцов, показывают, что относительные деформации в момент возникновения трещины и в момент разрушения (потери целостности) образца в основном зависят как от влажности, так и от диаметра. С уменьшением диаметра они несколько увеличиваются, как и с уменьшением влажности. Уравнения регрессии выражаются следующим образом:

ε₁⁽¹⁾ = 0,08743064 + 0,00123790L + + 0,00005097D² + 0,000007 3 3W²– –0,00007655DL – 0,00006439DW – – 0,00002243LW + 0,00000128DLW.

ε₁⁽²⁾ = – 0,19899810 + 0,01617315D + + 0,00976254L + 0,00272546W –

– 0,00004185L2 – 0,00030948DL –

– 0,00023143DW– 0,00005576LW + 0,00000404DLW.

Экспериментальные исследования анализа относительного объема частиц, полученных после разрушения, показывают, что относительный объем частиц значительно зависит от диаметра образцов и от их длины.

Уравнение регрессии зависимости объема частиц от влияющих факторов приведено ниже:

V_{отн ч} = 0,60069569 – 0,01594096D – 0,00584448L – – 0,^.0^. 0335709W + 0,00018685D² + 0,00004026L² +

+ 0,00008397DW + 0,00004184LW –   (11)

– 0,00000074DLW.

Предложенная математическая модель позволяет адекватно описывать стадии процесса разрушения древесины отходов лесозаготовок. На основании экспериментальных исследований получены регрессионные уравнения для растягивающих напряжений, относительных деформаций и относительного объема частиц.

Проведенная статистическая обработка экспериментальных данных позволила сделать вывод об адекватности модели многостадийного разрушения.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

REGULARITIES PROCESS OF THE WASTE WOOD DESTRUCTION