Закономерности процесса самоорганизации размерной структуры древостоев сосны обыкновенной

Актуальность и практическое значение исследований обусловлены необходимостью совершенствования способов и методов управления лесными экосистемами на основе познания законов их развития и самоорганизации. Априори принято считать, что лесные экосистемы, как и все биологические объекты, являются сложными открытыми динамическими системами, состоящими из тесно взаимодействующих между собой элементов; однако работа механизма их саморегуляции и самоорганизации раскрыта пока довольно слабо, что связано с очень большим разнообразием встречающихся экологических ситуаций [1–5]. Недостаток знаний в этой области отрицательно отражается на качестве управленческих решений и хозяйственных мероприятий, направленных на повышение производительности и устойчивости биологических систем к воздействию негативных природных и антропогенных факторов, а также к предотвращению ущерба от них.

Познание законов самоорганизации ценопо-пуляций древесных растений – сложная задача, требующая совместных теоретических и экспериментальных исследований. Для её решения необходимо создать математические модели этого процесса на основе обобщения огромного объёма информации о динамике размерной структуры древостоев и характере годичного прироста деревьев в разных экологических ситуациях. Теоретические и прикладные исследования по данному вопросу, эффективность которых во многом зависит от глубины и качества обработки накопленного эмпирического материала и степени его формализации, должны обязательно опираться на системный анализ [6], а также на основные принципы и законы популяционной экологии [1, 7–9], кибернетики [10, 11], текто-логии [12], синергетики и системологии [13–23].

Цель работы – исследование закономерностей процесса самоорганизации размерной структуры ценопопуляций сосны обыкновенной (Pinus sylvestris L.) и описание его соответствующими математическими уравнениями, адекватно отображающими изменения размерных характеристик древостоя и радиального годичного прироста деревьев.

Теоретические основы решения задачи

Создание любой научной теории идет от простого вербального описания объекта исследования, сбора и накопления фактов к их глубокому анализу, выполненному с помощью логических правил и математических методов. Кроме того, выявить закономерности самоорганизации структуры древостоев, под которой следует понимать характер изменения их внутренней упорядоченности за счёт согласованности действий всех элементов [24], невозможно без многолетних натурных наблюдений и проведения активных экспериментов.

В настоящее время в науках о лесе господствует эмпирический метод, позволивший, благодаря усилиям нескольких поколений исследователей, накопить колоссальный объём информации. Однако он не может в полной мере решить все важнейшие научные и практические задачи, если не будет дополнен созданием математических моделей природных объектов и протекающих в них процессов, на основе которых можно делать надёжные прогнозы и уверенно принимать управленческие решения, адекватные сложившейся обстановке.

Самоорганизация – процесс упорядочения в открытой системе исходного хаоса (пространственного, временного или пространственно-временного), протекающий за счёт согласованного изменения состояния всех её элементов на основе отрицательных обратных связей между ними, который определяется в большей степени их внутренними свойствами, нежели вариациями условий среды [3, 16, 24]. В каждой системе этот процесс может протекать с разной скоростью в зависимости от её исходного состояния и степени воздействия внешнего сигнала. Дифференциация деревьев в ценозах по диаметру – процесс сложный из-за наличия большого комплекса определяющих её факторов (возраст и наследственные свойства особей, условия произрастания насаждений, их густота и породный состав, лесохозяйственные мероприятия, вариации климата). Самоорганизация древесных ценозов проявляется в способности всей совокупности особей, исходно обладающих большим генетическим разнообразием [25, 26], расходиться по разным экологическим нишам, что позволяет им полнее использовать ресурсы внешней среды, оптимально заполняя пространство экотопа [3, 5]. По мере роста деревьев и в результате этого в ценозе образуются несколько дискретных групп, различающихся по морфологическим признакам и по-разному реагирующих на изменение условий внешней среды. Самоорганизация структуры древостоев – нелинейный процесс, протекающий стихийно с прохождением точек бифуркации (перелома) своего состояния за счёт разной скорости роста и естественного отбора особей [2], что неизбежно приводит к снижению внутреннего разнообразия ценопо-пуляций и их распаду. Многообразие элементов системы и их свойств является залогом её успешного развития [19, 20], а его уменьшение приводит к снижению возможностей естественного отбора и постепенной гибели сообщества [1, 27–30].

В процессе взаимодействия любого организма со средой, которое направлено на его адаптацию к сложившимся условиям среды и её флуктуациям, изменяется программа работы его генома, выражающаяся в смене нормы реакции на лимитирующие факторы в сложившейся экологической обстановке [31, 32], что сопровождается волновыми изменениями состояния всей системы [4, 23, 33–38], представляющими собой чередование фаз напряжённой работы и расслабления [39] и не являющимися строго периодическими. Сбой этого ритма приводит к нарушению протекания у деревьев физиологических процессов. Самоорганизация размерной структуры древостоев должна обязательно сопровождаться, как и во всех биосистемах, взаимной синхронизацией внутренних волновых процессов у всех входящих в его состав деревьев

[38], приводящей к образованию нескольких дискретных групп, различающихся по морфологическим признакам и по-разному реагирующих на изменение условий внешней среды [3, 40, 41], что способствует нивелированию динамики накопления биомассы всем сообществом [42].

Для формализованного строгого математического описания степени упорядоченности системы, т.е. соотношения в ней порядка и хаоса, в научных исследованиях опираются на две основные категории: симметрию и энтропию [18, 21, 24, 38, 43–45]. Процесс самоорганизации структуры любой системы, исходя из этого, можно оценить посредством изменения степени симметрии в системе, проявляющейся в чёткой повторяемости распределения не только элементов в пространстве, но и некоторых событий во времени. Энтропия же отображается рядом статистических показателей (среднеквадратического отклонения, коэффициентов вариации, асимметрии и эксцесса) тех или иных параметров у всех слагающих её элементов, значения которых в идеале должны приближаться к «нормальному» распределению Гаусса, имеющему центральную ось симметрии. Энтропия и симметрия изменяются всегда синхронно, но противоположно по отношению друг к другу.

Изучению особенностей формирования размерной структуры древостоев под действием факторов среды посвящено много публикаций [46–49], поскольку это важно для оценки ресурсной ценности насаждений, их жизнеспособности и возможностей дальнейшего развития, а также решения других лесоводственных задач. Большинство авторов отмечают очень большую вариабельность всех статистических параметров рядов распределения деревьев по размерам, однако ни в одной работе они не заостряют внимание на биологическом смысле статистических параметров размерной структуры древостоев, ограничиваясь в основном констатацией их абсолютной величины и сопоставлением значений с моделью так называемого нормального распределения, при котором асимметрия (А) и эксцесс (Е) стремятся к нулю. Следует отметить, что это распределение, впервые выявленное Муавром в 1733 г. и вновь обнаруженное в 1809 г. Гауссом, а в 1812 г. также Лапласом, в связи с их работой по теории ошибок наблюдений [50], является лишь идеальной формой отображения вероятности встречаемости той или иной величины какого-либо признака в оцениваемой совокупности его значений. Это распределение предполагает, что все факторы, воздействующие на систему, уравновешивают друг друга по силе, и используется для сравнения теоретических данных с фактическими. При его применении различия отражают лишь ошибку в оценке статистических параметров, а не явное проявление особенностей внутренней структуры объекта. Преобладание воздействия на систему какого-либо одного фактора над другими приводит к деформации нормального распределения и превращению его в иную форму.

Процесс самоорганизации структуры древостоя протекает довольно медленно, поэтому для познания его закономерностей необходимо располагать данными о её многолетних изменениях на стационарных объектах мониторинга. Менее пригоден для этого традиционный метод формирования временных́ рядов на основе сбора материала в древостоях разного возраста, поскольку он не позволяет учесть влияние исходного состояния ценопопуляций, которое во многом может определять ход их дальнейшего развития. Для изучения процесса самоорганизации размерной структуры древостоев целесообразно использовать ряды значений текущего годичного прироста деревьев в высоту и по диаметру, позволяющие ретроспективно и одномоментно оценить характер происходящих изменений за очень длительный период времени [51, 52]. Влияние на рост деревьев факторов среды изучено к настоящему времени довольно хорошо [2, 52], что нельзя сказать о роли в этом процессе эндогенных механизмов, хотя именно они обусловливают формирование структуры древостоев [53]. Ход роста каждого дерева, как показали наши исследования [2, 54–56], сугубо индивидуален, что подтверждает в целом выводы других исследователей [57–64]. Доля участия той или иной группы деревьев, различающихся по характеру динамики их радиального прироста, в каждой ценопопуляции неодинакова.

Рост дерева – сложный самоуправляемый процесс реализации его потенциальных возможностей, т.е. развертывания во времени уже существующих задатков [65], заложенных в генотипе, который характеризуется как увеличением его размеров, так и степенью организованности всех внутренних структур. Биологический смысл роста дерева, как и любого организма, заключается в достижении им определённых размеров, обеспечивающих ему, согласно закону оптимальности [9], максимально эффективную реализацию всех необходимых жизненных функций в эволюционно сложившемся биотическом окружении и экологической обстановке [2]. Полное представление о процессе самоорганизации размерной структуры древостоев может быть получено лишь на основе анализа изменения размера слагающих их деревьев и текущего годичного прироста. Описать рост дерева с высокой точностью каким-либо одним достаточно простым уравнением принципиально невозможно, поскольку он представляет собой процесс виртуальных (возможных) перемещений системы, протекающий исходя из имеющихся связей и причинно-следственных отношений, определённых вариациями параметров среды и рядом биологических ограничений. Естественные «шумы», возникающие вследствие флуктуаций и периодических колебаний климата, настолько велики, что создать модели с погрешностью ±5–10% бывает просто невозможно в принципе. Полная математическая модель роста дерева представляет собой некоторую аддитивную смесь функций возрастного тренда, волновой составляющей и случайной «шумовой» компоненты [2]. Каждая из этих составляющих будет зависеть от потенциальных возможностей дерева, заложенных в его генотипе, и динамики состояния всей экосистемы, в том числе густоты древостоя [52, 66–72].

Развитие древостоя, как и любой популяции организмов, обязательно сопровождается гибелью некоторой части особей в результате жесточайшей борьбы за существование или, правильнее сказать, жизненного состязания за обладание ресурсами среды (энергией, веществом и пространством), которые всегда ограничены определёнными пределами. Этот процесс в лесоводстве принято называть естественным изреживанием древостоев. Он является частным, но необычайно показательным случаем проявления закона естественного отбора, общность которого для всего живого убедительно показал Ч. Дарвин [73]. Без борьбы за существование, без естественного отбора немыслима эволюция биоты, т.е. её прогрессивное развитие [74], направленное на повышение устойчивости к изменениям условий среды и степени соответствия всем её требованиям. Роль конкуренции деревьев за свет, влагу и элементы питания, которая обычно рассматривалась исследователями в качестве основного механизма саморегуляции структуры древостоя, подвергается в настоящее время сомнению в результате выявления примеров сотрудничества или кооперации между ними, осуществляемых посредством срастания корневых систем [75–78]. Для деревьев не существует понятия собственного «я», а есть понятие «мы», суть которого заключается в обеспечении выживаемости вида. В ходе естественного изре-живания древостоев, которое является ярким отражением процесса его саморегуляции, самонастройки на существующие условия среды, на минимизацию отрицательных воздействий слагающих его элементов друг на друга и достижение определённой гармонии отношений между ними, происходит разрешение противоречий (постоянно имеющих место в жизни) между потребностями деревьев и возможностями среды их обитания.

Необходимость познания закономерностей естественного изреживания древостоев, теснейшим образом связанного с течением всех остальных процессов жизнедеятельности лесных экосистем и описанного многими исследователями [65, 79–83], не нуждается в особых доказательствах, поскольку с этим процессом связаны многие задачи теории и практики лесоводства. Моделирование динамики лесных экосистем, необходимое для выбора оптимальных режимов их выращивания и стратегий использования, немыслимо без учёта этого процесса [84–87], на биофизический смысл которого серьёзное внимание впервые обратил Г.Ф. Хильми, математически проанализировав его в своих работах [66–68]. К настоящему времени создано уже несколько десятков математических моделей, описывающих особенности протекания этого процесса в зависимости от исходной густоты древостоя, во многом определяющей, благодаря наличию механизма саморегуляции, темп его изреживания [2]. Установлено, к примеру, что густота так называемых нормальных древостоев представляет собой некоторый предел, являющийся совсем не нормой, а скорее аномалией [85, 88–90], поскольку они в этом состоянии, которое является крайне неустойчивым, долго находиться не могут. Предложены также модели, в которых процесс изреживания древостоев представлен функцией средней высоты деревьев [91].

Материалы и методы исследования

Эмпирический материал для анализа собран на 284 постоянных и временных пробных площадях, заложенных в чистых одновозрастных сосновых древостоях Республики Марий Эл, которые различаются между собой по происхождению, возрасту (от 12 до 120 лет), густоте (от 0,5 тыс. до 103 тыс. экз./га) и условиям произрастания. На каждой из пробных площадей было не менее 200 живых деревьев, распределённых при перечёте по ступеням толщины и классам развития Г. Крафта. Дополнительно на 17-ти постоянных пробных площадях с полностью пронумерованными деревьями периодически один раз в 5 лет измеряли длину окружности ствола и оценивали текущий прирост по диаметру (общая продолжительность наблюдений на них варьировала от 10 до 40 лет). Также была использована электронная база данных, содержащая детальную таксационную характеристику насаждений всех лесничеств республики (более 400 тыс. выделов общей площадью 1 165 628 га), из которой были выбраны древостои с преобладанием сосны, произрастающие в сухих и свежих борах (32 118 таксационных выделов). Материал, содержащийся в базе данных, сортировали по возрасту древостоя и для каждой выделенной группы вычисляли статистические показатели средних значений диаметра и высоты, а также густоты (N, экз./га), полученной расчётным путем на основе подобранного нами [52, 92, 93] уравнения регрессии:

N = M : [3,583 x 10^-5 x H °. ⁹⁹² x (d + 1) 2 ],    (1)

где:

N - густота древостоя, тыс. экз. х га^-1,

M – запас стволовой древесины, м3/га;

Н – средняя высота древостоя, м;

D – средний диаметр древостоя, см;

Ошибка уравнения не превышает ±5 %.

Для анализа динамики радиального годичного прироста деревьев из сформированной нами обширной электронной базы данных [94] были отобраны 200 экземпляров I и II классов Крафта, произрастающих на 26 пробных площадях в сосняках лишайниковых, лишайниково-мшистых и брусничниковых Республики Марий Эл. Цифровой материал обработан на персональном компьютере с использованием пакетов прикладных программ Excel и Statistica, позволяющих стандартными методами биометрии [50, 95–99] осуществить расчёт элементарных статистических показателей, а также дисперсионный, корреляционный, кластерный и регрессионный анализы. При исследовании процесса самоорганизации размерной структуры древостоев оценивали изменение величины среднеарифметического, среднеквадратического (стандартного) отклонения, коэффициентов вариации, асимметрии и эксцесса диаметра стволов деревьев и их текущего прироста в ценопопуляциях.

Результаты и обсуждение

Анализ эмпирического материала показал, что все значения параметров размерной структуры древостоев сосны, произрастающих в сухих и свежих борах Республики Марий Эл, закономерно изменяются с увеличением возраста [54], что описывают соответствующие математические модели (табл. 1). Так, средняя высота и средний диаметр древостоев неуклонно приближаются к своему верхнему пределу,

Таблица 1. Возрастные изменения статистических параметров сосновых древостоев в сухих и свежих борах Марийского Заволжья

Параметр*	Значения параметров древостоя в разных группах возраста, лет
	21–40	41–60	61–80	81–100	101–120	121–140
n	10 615	9 965	7 093	2 588	1 245	612
Средняя высота древостоя, м
М	10,0	17,3	21,4	24,2	24,7	24,4
min	3	8	14	17	18	17
max	19	28	29	30	30	29
S	2,33	2,30	1,76	1,70	1,88	1,67
CV	23,2	13,3	8,2	7,0	7,6	6,9
А	0,189	-0,026	-0,012	0,069	-0,009	-0,173
Е	-0,237	-0,433	-0,216	0,786	0,027	-0,286
Средний диаметр древостоя, см
М	10,6	17,8	23,4	28,9	32,2	34,5
min	4	6	14	20	20	20
max	22	28	36	40	48	52

Окончание табл. 1

Параметр*	Значения параметров древостоя в разных группах возраста, лет
	21–40	41–60	61–80	81–100	101–120	121–140
S	2,26	2,85	2,68	3,27	3,37	4,30
CV	21,4	16,0	11,5	11,3	10,5	12,5
А	0,263	0,304	0,184	0,154	0,470	0,056
Е	0,004	-0,021	-0,191	0,181	0,948	0,043
Густота древостоя, тыс. экз./га
М	2,13	0,96	0,56	0,35	0,25	0,19
min	0,08	0,09	0,14	0,10	0,08	0,04
max	12,3	3,98	1,43	0,99	0,61	0,66
S	0,89	0,34	0,16	0,11	0,08	0,07
CV	41,7	34,9	28,9	32,0	31,2	37,8
А	1,561	1,058	0,611	0,848	0,654	1,272
Е	4,997	2,613	0,615	1,188	0,827	3,709

Примечание: n – объем выборки (количество таксационных выделов), М – среднее арифметическое значение оцениваемого показателя; min , max – минимальное и максимальное значения показателя; S – среднеквадратическое (стандартное) отклонение вариационных рядов; CV – коэффициент вариации значений показателя в выборке, %; А , Е – коэффициенты асимметрии и эксцесса вариационных рядов.

ограниченному условиями среды, а их густота, наоборот, снижается, что аппроксимирует уравнение регрессии:

N = 9,68xexp[-0,113x(A-10)] + 0,633;

R ² = 0,665,                 (2)

где А – возраст древостоя, лет.

В пределах каждой группы возраста древостоев отмечается, как свидетельствуют данные табл. 1, очень значительное варьирование каждого из этих показателей, обусловленное различиями густоты ценопопуляций и генетическими особенностями входящих в них особей. Расчёты показали, что величина среднеквадратического отклонения средней высоты древостоев и их густоты с возрастом неуклонно снижается, среднего диаметра, наоборот, увеличивается. Тенденция же к уменьшению коэффициента вариации чётко проявляется у показателей средней высоты, среднего диаметра и густоты древостоев. Величина коэффициентов асимметрии и эксцесса рядов всех оцениваемых параметров изменяется с возрастом древостоев в основном волнообразно, что связано с достижением ими определённых точек неустойчивости (бифуркации), после которых происходит резкое ускорение процесса дифференциации деревьев вследствие повышения темпов отмирания ослабленных особей. Один из таких этапов развития древостоев, связанный с массовым размножением в лесах Марий Эл сосновой вершинной смолёвки (Pissodes piniphilus Hrbst.) и детально проанализированный нами [54, 100–102], отмечался в 1981–1991 гг.

Анализ литературных источников [91, 103– 105] и проведённые нами расчёты [106] показали также, что основные таксационные параметры древостоев функционально связаны со средней высотой деревьев, являющейся одним из важнейших индикаторов процесса самоорганизации размерной структуры ценопопуляций. Эту связь отражают следующие уравнения регрессии:

N = 30,9xexp(-0,381xH) + 0,756; R 2 = 0,730, (3)

D = 1,304х(Н -1,3) + 0,756; R 2 = 0,970,   (4)

где:

Н – средняя высота древостоя, м;

D – средний диаметр древостоя, см.

Линии, отображающие зависимость таксационных параметров древостоя от высоты, соответствуют региональной «норме», отклонения от которой характеризуют особенности конкретных ценопопуляций. Особую хозяйственно-селекционную ценность будут представлять древостои с большим положительным отклонением, максимально возможные значения которого ограничиваются линией, описываемой соответствующими уравнениями регрессии:

N = 48,3xexp(-0,223xH),       (5)

D = 2,45 x(H - 1,3) ⁰’⁹²² .           (6)

Приближение параметров древостоя к этой линии свидетельствует о наступлении резкого перелома в ходе развития древостоя и увеличении текущего отмирания деревьев из-за избыточной густоты ценопопуляции.

Однако результаты, полученные на основе таксационных описаний древостоев, отражают в большей степени разнообразие параметров древостоев в имеющейся совокупности выделов, чем фактический характер динамики их размерной структуры. Для адекватного же представления о внутриценотических процессах необходимо оценивать реальную размерную структуру древостоев или анализировать ряды многолетних наблюдений на постоянных пробных площадях. Исследования, проведённые нами по этой схеме, показали, что все параметры одновозрастных древостоев сильно варьируют в зависимости от их густоты, однако прослеживаются те же самые общие закономерности их изменения во времени. Так, средний диаметр древостоя (Dср.) и его среднеквадратическое отклонение (SD) увеличиваются с возрастом, а значения коэффициентов асимметрии и эксцесса изменяются волнообразно, что подтверждает версию о неравномерности развития древостоев и наличии в ходе их самоорганизации точек бифуркации, связанных с перестройкой их размерной структуры (табл. 2). Изменение таксационных параметров древостоев

Таблица 2. Характер возрастных изменений статистических параметров густоты древостоя и диаметра деревьев на объектах исследования

Параметр*	Значения параметров древостоя в разных группах возраста, лет
	12–20	21–40	41–60	61–80	81–100	101–120
k	108	65	75	16	25	12
Густота древостоя, тыс. экз./га
М	7,83	3,94	3,24	1,18	0,75	0,59
min	0,50	0,50	0,50	0,49	0,42	0,50
max	103,1	13,70	25,40	2,50	1,16	0,83
Средний диаметр деревьев, см
М	5,8	10,2	13,6	18,8	25,0	29,7
min	2,2	3,9	2,5	10,3	18,6	25,8
max	13,7	19,5	24,9	26,4	30,6	32,5
Среднеквадратическое отклонение диаметра деревьев, см
М	2,11	3,16	3,77	5,33	5,86	6,22
min	1,09	1,55	1,47	3,69	4,66	5,13
max	3,06	4,30	7,45	8,26	8,60	7,27
Коэффициент вариации диаметра деревьев, %
М	38,8	31,6	30,0	28,8	23,7	21,0
min	16,7	18,9	17,9	20,6	17,2	17,7
max	58,6	45,7	74,9	37,2	34,1	28,2

Окончание табл. 2

Параметр*	Значения параметров древостоя в разных группах возраста, лет
	12–20	21–40	41–60	61–80	81–100	101–120
Коэффициент асимметрии вариационных рядов диаметра деревьев
М	0,014	0,297	0,409	0,514	0,309	0,230
min	-1,140	-0,973	-0,567	-0,111	-0,304	0,071
max	1,275	0,930	1,348	1,048	0,625	0,421
Коэффициент эксцесса вариационных рядов диаметра деревьев
М	-0,331	-0,123	-0,045	0,073	-0,222	-0,260
min	-1,125	-0,847	-1,068	-0,643	-0,705	-0,582
max	1,615	1,559	1,960	0,991	0,842	0,326

*Примечание: k – объем выборки (количество пробных площадей), обозначение остальных параметров как в табл. 1.

в зависимости от их возраста (А, лет) и текущей густоты (N, тыс. экз.хга -1 ) аппроксимируют следующие уравнения регрессии:

D_ср = 2,418xA 0-⁵³7 xexp(-ii,5xio ^-2 xN),

R ² = 0,931.                 (7)

S D = 0,832xА ⁰■⁴³⁷ xexp(-4,46x10 ^-2 xN),

R ² = 0,859.                (8)

Многолетние наблюдения за процессом самоорганизации размерной структуры древостоев, проведённые на стационарном опытном объекте [107], показали, что исходная их густота

0s co co Ф ct

CC

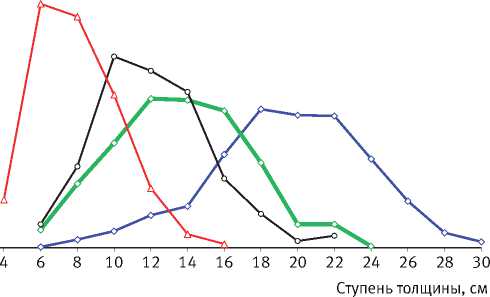
3 тыс. экз. га

10 тыс. экз. га

0,5–1,0 тыс. экз./га

5 тыс. экз./га

оказывает очень большое влияние на характер распределения деревьев по диаметру (рис. 1). Так, при свободном стоянии деревьев в варианте с самой низкой густотой посадки полностью раскрывается их жизненный потенциал, который в загущенном древостое подавлен. По мере развития древостоев волнообразно изменяются также значения коэффициентов асимметрии и эксцесса рядов распределения диаметра деревьев (рис. 2), причиной чего является цикличность процесса их дифференциации, происходящего стохастично и, в связи с этим, труднопрогнозируемого. Математические модели динамики среднего и максимального диаметра деревьев ( D_cр и D_max , см) в культурах разной густоты ( N , тыс. экз./га), а также значений среднеквадратического отклонения этого таксационного параметра древостоя ( S _D, см) имеют следующий вид:

D ср = 1,816x( А - 5) ⁰,W*expt-⁰,°4⁷*N) ;

R2 = 0,935; р < 0,001,(9)

D max = 2,683x( А - 5) ⁰.^703xexpt^-0.^033xN ) ;

R2 = 0,917; р < 0,001,(10)

S D = 0,60x( А - ₅) ⁰,^587xexpt^-0,^033xN ) ;

R2 = 0,674; р < 0,01.(11)

Рис. 1.

Характер распределения деревьев по ступеням толщины в 40-летних культурах сосны разной исходной густоты

Исходная густота культур существенно влияет также на динамику значений относительной протяжённости крон деревьев ( h , %), площади

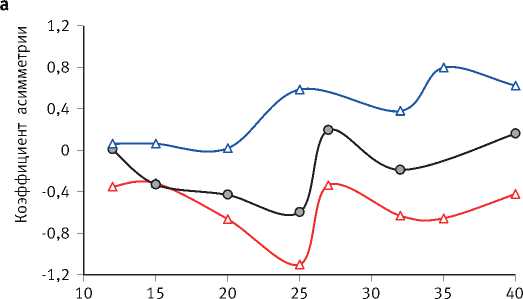
Возраст, лет

0,5–1,0 тыс. экз./га

Возраст, лет

3–5 тыс. экз./га

10 тыс. экз./га

Рис. 2. Динамика коэффициентов асимметрии (а) и эксцесса (б) рядов диаметра деревьев в культурах сосны разной исходной густоты их проекции (S, м2), продолжительности жизни нижних ветвей (Аветв, лет), динамику их длины (L, см) и величину её среднеквадратического отклонения (SL, см), что наилучшим образом описывают следующие уравнения регрессии:

h = 80хехр(-11,41х10 ^-4 х( А — 5) 2 х N 0.5 ) + 20;

R2 = 0,916.(12)

S = 1,253хехр(-88,76х10 ^-3 х N) х D 0.⁸²² ;

R2 = 0,806.(13)

А ветв = 30хехр(-72,54х10 ^-3 х N ) х

х[1 - ехр(-33,91х10 ^-3 х А )];

R2 = 0,865.(14)

L = 432хехр(-11,83х10 ^-2 х N ) х

х[1 - ехр(-89,7х10 ^-3 х Ах N ⁰.²⁵ )];

R2 = 0,98.(15)

S L = 50,2хехр(-33,30х10 ^-3 х N) х х[1 - ехр(-10,91х10 ^-2 х А )];

R2 = 0,93.(16)

Анализ этих уравнений показывает, что в результате отмирания нижних ветвей деревьев протяженность их кроны во всех вариантах опыта к 80-летнему возрасту культур устанавливается в пределах 20–30% общей длины ствола. Площадь проекции кроны деревьев в варианте самой низкой густоты в этом возрасте будет в 5,6 раза выше, чем в наиболее густых, достигая 22,7 м2. Средняя продолжительность жизни нижних ветвей при низкой густоте будет составлять 26–27 лет, а их длина – 390 см, а в густых культурах – соответственно 13–14 лет и 130 см.

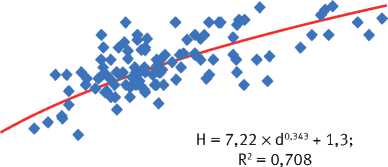
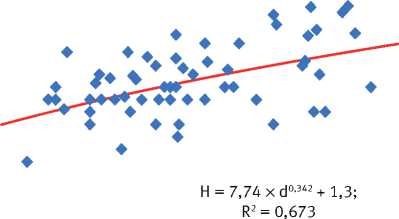
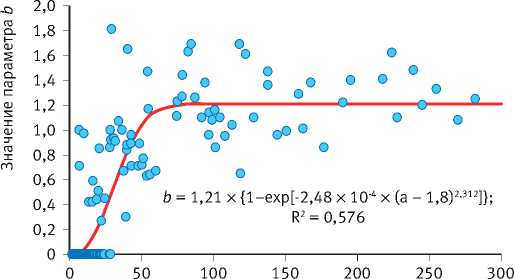
На основе анализа материалов исследований на постоянных и временных пробных площадях было установлено наличие физиологически обусловленной зависимости высоты дерева ( h , м) от его диаметра на высоте 1,3 м ( d , см), наиболее адекватно в пределах каждого древостоя описываемой степенным уравнением h = ах d b + 1,3 (рис. 3), параметры которого имеют конкретный биофизический смысл: а – скорость изменения значений h в градиенте значений диаметра ствола, b – ускорение изменения значений h от d . Величина этих параметров не является постоянной, а варьирует на объектах исследования в довольно широких пределах (табл. 3). Особенно велика изменчивость параметра a , который тесно сопряжён с значением параметра b ( R ² = 0,896), что указывает на определённую организованность ценопопуляций деревьев.

Каков же физиологический механизм, вызывающий изменение величины отношения между высотой деревьев и их диаметром? Почему в худших условиях их произрастания его величина выше, чем в лучших? Почему с увеличением возраста древостоев она резко снижается

а

Высота дерева, м

10      15      20      25      30      35      40

Диаметр дерева, см

Диаметр дерева, см

Рис. 3. Характеристика соотношения между диаметром и высотой деревьев на объектах исследования в свежих борах заповедника «Большая Кокшага»:

а – естественный древостой, 80 лет: б – лесные культуры, 110 лет

Таблица 3. Вариабельность значений параметров уравнения, описывающего зависимость высоты деревьев от диаметра ствола на объектах исследования

Параметр уравнения h = a x db + 1,3 Значения статистических показателей оцениваемых параметров M ± m min max S CV, % Параметр a 5,156 ± 0,635 0,172 23,89 5,314 103,1 Параметр b 0,458 ± 0,026 0,026 1,295 0,217 47,4 Коэффициент детерминации R2 0,560 ± 0,029 0,040 0,909 0,247 44,1 Ошибка оценки, % 7,75 ± 0,36 2,30 17,1 2,984 38,5 и стабилизируется после 60 лет? Концепция об отражении этим параметром степени требовательности деревьев к свету, выдвинутая и поддерживаемая многими исследователями, объяснить этого не может. Рост деревьев зависит, как известно, не только от светового довольствия, но и от степени обеспеченности их крон водой. Чем выше поднята крона деревьев, тем больше им нужно затратить энергии на подачу воды к ней и тем больше у них должна быть площадь водопроводящей зоны ствола, что может быть достигнуто только за счёт увеличения их диаметра.

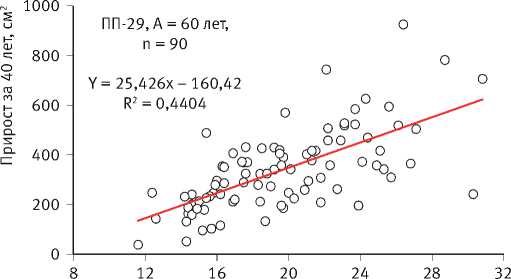
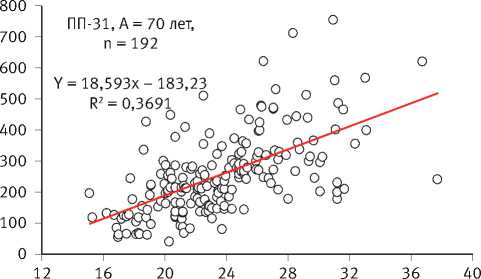
Многолетние мониторинговые исследования на стационарных объектах показали, что отмирание деревьев происходило по ярко выраженному низовому типу за счёт отставших в росте особей [54], а динамика прироста каждой из сохранившихся являлась сугубо индивидуальной и очень слабо зависела от их исходного диаметра на начало наблюдений, свидетельствуя о непрерывно текущем процессе формирования размерной структуры ценопопуляций и невозможности уверенного прогнозирования изменения размеров каждой особи в них (рис. 4). Это подтвердил также анализ динамики радиального прироста деревьев в имеющейся у нас базе данных [94].

Каковы же причины дифференциации деревьев в ценопопуляциях? В настоящее время среди учёных преобладает концепция, согласно которой полиморфизм древесных растений по размерам обусловлен наследственными причинами, а конкуренция лишь усиливает их исходное неравенство [40, 108]. Такое объяснение этого процесса не подкреплено, однако, материалами генетических исследований и не вскрывает сути происходящих изменений. Некоторые исследователи [41, 109–112] считают, что разные темпы роста деревьев могут определяться неодинаковой способностью особей к резервированию в своих

Диаметр дерева в 1983 г., см

Диаметр дерева в 1983 г., см

ПП-30, А = 80 лет, n = 286

24,413x – 218,9 R2 = 0,4263

Y =

Диаметр дерева в 1983 г., см

Y =

ПП-34, А = 90 лет, n = 238

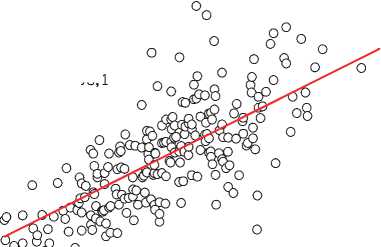
Диаметр дерева в 1984 г., см

10,903x – 108,1 R2 = 0,5194

Рис. 4. Влияние исходного диаметра деревьев на объектах мониторинга в сосняках брусничниковых на их прирост по площади сечения ствола органах ресурсов питательных веществ и их распределению между ними. Быстрорастущие особи основную часть аккумулированной солнечной энергии вкладывают в прирост древесной массы и не создают якобы долговременные запасы питательных веществ, а медленнорастущие, наоборот, оставляют их в резерве. Это заключение также не подтверждено данными о наличии запасов питательных веществ в тех или иных органах растений и характера их транспортирования от кроны к корням.

Для получения ответа на вопрос о причинах дифференциации деревьев по диаметру необходимо, на наш взгляд, осуществить детальный анализ динамики их радиального годичного прироста. Исследования показали, что разделение деревьев по скорости роста происходит довольно рано и различия между ними по диаметру с возрастом становятся всё значительнее (рис. 5). Эта закономерность не вскрывает, однако, причин происходящих изменений, а лишь отражает их последствия. Регрессионный анализ рядов радиального прироста господствующих в цено-популяциях деревьев показал очень большую неоднородность характера динамики их радиального прироста, описываемой в подавляющем большинстве случаев (85,5%) отрицательным экспоненциальным уравнением:

Y = K x exp (- a x10 ’3 x A ) + b ,        (17)

где:

Y – величина годичного радиального прироста, мм;

К – величина прироста дерева в первый год образования годичного кольца;

a – темпы снижения прироста во времени;

b – нижний уровень стабилизации величины годичного прироста.

значения параметров которого представлены в табл. 4. Оказалось, что из 200 проанализированных деревьев I и II классов Крафта всего

а

Годичный прирост, мм

I и II                   III

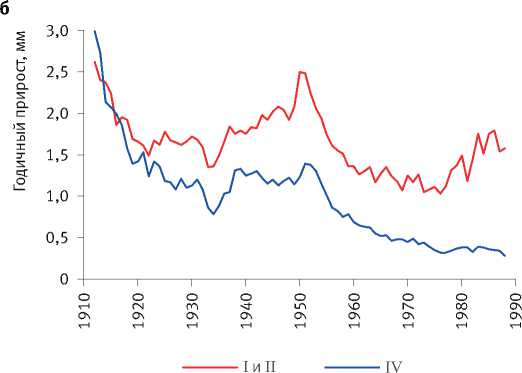
Рис. 5. Динамика радиального прироста деревьев сосны разных классов Крафта в молодых культурах ( а ) и древостое естественного происхождения ( б )

Таблица 4. Вариабельность значений параметров уравнения, описывающего динамику радиального годичного прироста деревьев сосны в исследуемой выборке

Параметр уравнения Значение статистических показателей параметров уравнения Y = Kх exp (- a xio-3xa) + b M ± m min max S CV, % K 3,62 ± 0,19 0,77 18,75 2,50 69,0 a 68,1 ± 7,69 1,87 463,8 100,5 147,7 b 0,53 ± 0,04 0,00 1,81 0,59 111,1 R2 0,529 ± 0,018 0,028 0,956 0,234 44,2 лишь у 2,5% возрастной тренд отклонялся от этой закономерности, а у 12% он практически отсутствовал. Параметры этого уравнения, имеющие конкретный биофизический смысл и большую информационную ценность, можно использовать для анализа особенностей размерной структуры древостоев и процессов её самоорганизации. Особенно изменчив характер роста деревьев, как свидетельствуют приведённые данные, по величине параметров a и b, ряды значений которых в определённой мере сопряжены между собой (рис. 6). Наиболее часто встречаются в выборке деревья, довольно медленно снижающие величину годичного прироста, значение параметра a уравнения возрастного тренда у которых не превышает 30 единиц (рис. 7). Доля же деревьев с очень быстрым снижением прироста, которые неизбежно отмирают, не превышает 15%.

Тесно связаны между собой также значения параметров К и коэффициента детерминации R ² уравнения, который обратно пропорционален степени отзывчивости деревьев на изменение условий среды. Деревья с чётко выраженным возрастным трендом годичного прироста ( R ² > 0,6) обладают низкой конкурентоспособностью и неизбежно отмирают в процессе развития ценопопуляций. Они также слабо реагируют на колебания условий среды. Деревья же со слабо-выраженным возрастным трендом ( R ² < 0,6) более конкурентоспособны, но чутко реагируют на колебания климата, что вовсе не является их положительным качеством по отношению к первой группе особей, поскольку их постоянное приспосабливание к текущим погодным условиям не гарантирует успешного развития в будущем, которое в принципе практически не предсказуемо. В особенно невыгодном положении они

Значение параметра а

1,0

0,8

0,6

0,4

0,2

10           15

Значение параметра K

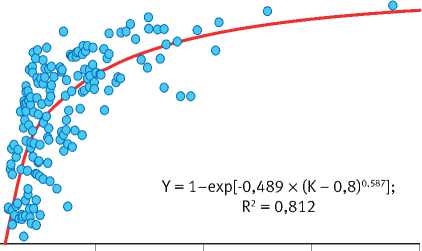
Рис. 6. Характер связи между рядами значений различных параметров уравнения возрастного тренда динамики радиального годичного прироста деревьев в сосняках брусничниковых Марий Эл

Значение параметра а

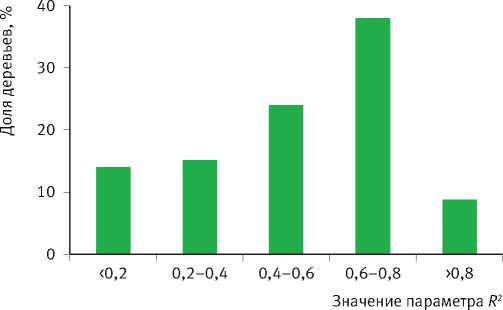
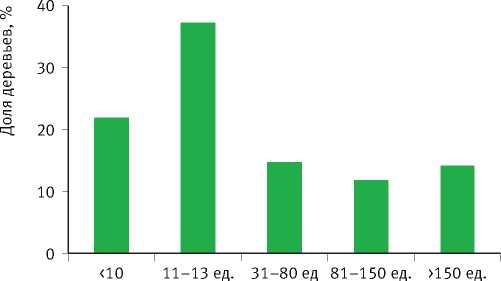
Рис. 7. Гистограммы распределения деревьев в выборке по значениям параметров уравнения возрастного тренда их радиального годичного прироста

будут находиться после сильных засух и других природных аномалий. В результате присутствия в ценопопуляциях экологически разных групп деревьев неизбежно будет происходить, на основе закона Г.Ф. Гаузе [по 9], конкурентное исключение одной из них, что во многом определяет процесс самоорганизации размерной структуры древостоев, полностью подтверждающий справедливость закона единства и борьбы противоположностей.

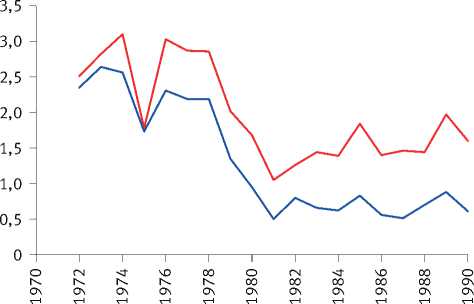
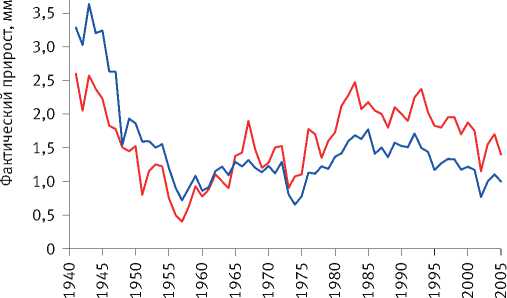
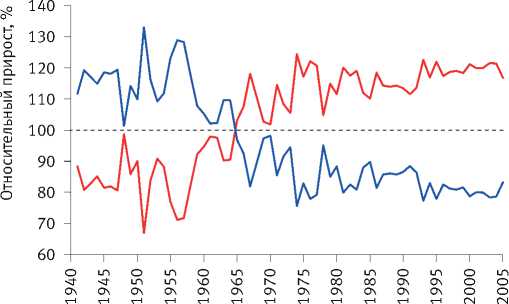
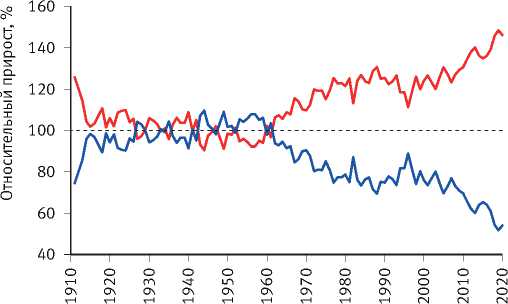
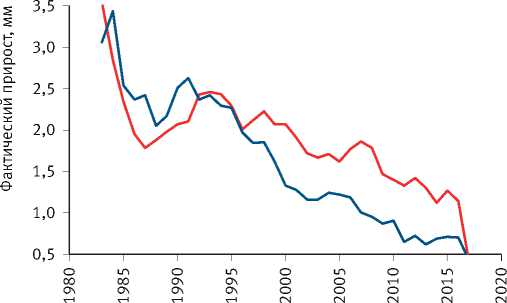
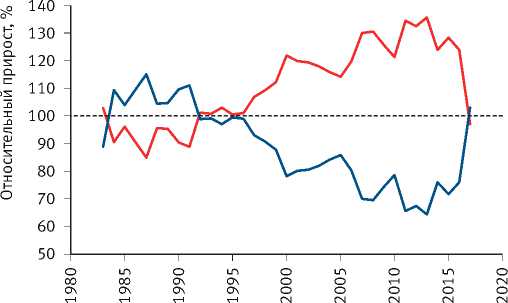
Расчёты показали, что разделение экологически различающихся групп деревьев по величине их радиального прироста произошло на объекте исследования в сосняке зелёномош-никовом в 1965 г. и значительно усилилось после засухи 1972 г. (рис. 8). Сходная картина отмечена и на других объектах. Так, к примеру, в сосняке брусничниковом кластеризация рядов радиального прироста деревьев, проведённая по его среднему значению за последние 10 лет, показала, что их разделение на размерные группы началось в 1960 г., задолго до засухи 1972 г. (рис. 9). Причиной этого стало снижение темпов роста древостоев, начавшееся в 1950 г., как было показано нами [52], в результате глобальных изменений климата, связанных с извержениями вулканов, к которым деревья оказались более чувствительными, чем используемые метеорологами приборы и методы. Чёткое разделение деревьев на разные группы по характеру динамики их радиального прироста произошло также после интенсивного изреживания древостоев, проведённого на объекте исследования в 1990 г. (рис. 10). Однако через 25 лет между особями

R2<0,6

R2>0,6

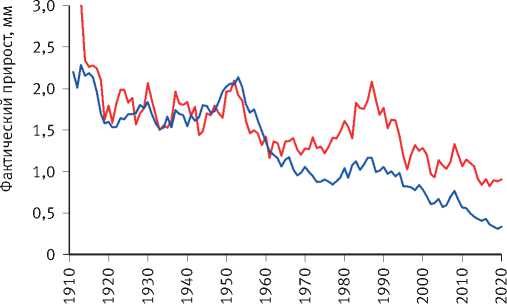
Рис. 8. Динамика радиального прироста деревьев в сосняке зелёномошниковом естественного происхождения, различающихся по величине коэффициента детерминации возрастного тренда

Высокий, n = 10                 Низкий, n = 18

Кластер 1

Рис. 10. Динамика радиального годичного прироста деревьев разных кластеров на объекте исследования в густых культурах сосны при высокой интенсивности их изреживания (68–80%)

Рис. 9. Динамика радиального прироста деревьев в сосняке брусничниковом естественного происхождения, различающихся по его среднему значению за последние 10 лет

Кластер 2

в ценопопуляции вновь установился паритет, что связано с возросшей конкуренцией их за жизненное пространство в биотопе, на которое они реагируют по-разному.

Изменение величины годичного прироста деревьев происходило, как свидетельствуют приведённые данные, всё время асинхронно по отношению друг к другу, что указывает на различие их ответных реакций на колебания параметров климата. В результате этих различий, которые с большой вероятностью обусловлены генетически, одна группа особей получает преимущество в освоении ресурсов среды над другой, не способной уже восстановить паритет после длительного периода угнетения. Доля участия этих групп деревьев в сложении структуры разных ценопопуляций неодинакова, что существенно отражается на усреднённой картине динамики их радиального прироста.

Выводы

Анализ литературных источников и материалов наших многолетних исследований позволяет сделать следующие выводы:

• 1.    Под самоорганизацией размерной структуры древостоев следует понимать процесс изменения их внутренней упорядоченности за счёт способности генетически разнородных групп деревьев расходиться по собственным экологическим нишам в результате согласованного изменения динамики их радиального годичного прироста, осуществляемый посредством механизма отрицательных обратных связей. Этот процесс, направленный на повышение эффективности использования ценопопуляциями ресурсов среды, обусловлен в большей степени их внутренними свойствами, нежели вариациями климата и внешних воздействий. Он протекает нелинейно с прохождением ряда точек бифуркации и неизбежно приводит к снижению исходного генетического разнообразия в ценопопуляциях, завершаясь распадом старого поколения деревьев.

• 2.    В ходе самоорганизации размерной структуры ценопопуляций происходит внешне хорошо

• 3.    Основными предикторами прироста объёма и массы стволовой древесины в цено-популяциях сосны обыкновенной являются абсолютно сухая масса хвои деревьев и площадь поверхности их камбия, которые изменяются с возрастом нелинейно, достигая максимальных значений в 40–50 лет, что описывают соответствующие уравнения регрессии. Эти параметры древостоев функционально связаны со средней высотой деревьев, линии регрессионной зависимости которой соответствуют региональной «норме» развития ценопопуляций. Большое положительное отклонение от неё свидетельствует о приближении древостоя к точке бифуркации развития и неизбежном резком переломе его хода, наступающем чаще всего из-за избыточной густоты ценопопуляции.

• 4.    Процесс самоорганизации размерной структуры древостоев целесообразно оценивать по изменению величины среднеквадратического отклонения диаметра деревьев в ценопопуля-циях, неуклонно увеличивающейся с их возрастом, а также коэффициентов асимметрии и эксцесса рядов распределения этого таксационного параметра, значения которых изменяются волнообразно. Для выявления закономерностей протекания этого процесса в ценопопуляциях целесообразно использовать также анализ дендрохронологических рядов разных групп деревьев.

• 5.    Деревья в ценопопуляциях сильно различаются между собой по темпам роста и степени

выраженная дифференциация деревьев на ряд дискретных групп, наследственно отличающихся по экологическим требованиям к условиям среды, одна из которых получает преимущество в освоении её ресурсов над другой, не способной уже восстановить паритет после длительного периода угнетения. В каждой ценопопуляции этот процесс протекает по-разному в зависимости от их исходной густоты и доли участия генетически разных групп деревьев, а также силы воздействия внешнего сигнала и его направленности. Жизненный потенциал деревьев полностью раскрывается при низкой густоте древостоев, при избыточной же их густоте он сильно подавляется.

выраженности возрастного тренда радиального прироста. Деревья с чётко выраженным возрастным трендом (R2 > 0,6) обладают низкой конкурентоспособностью и слабо реагируют на колебания условий среды. Они неизбежно отмирают в ходе развития ценопопуляций. Деревья же со слабовыраженным трендом (R2 < 0,6) чутко реагируют на колебания климата и более конкурентоспособны. Рост каждого дерева, однако, сугубо специфичен и точный долгосрочный прогноз изменения диаметра его ствола практически невозможен.

Финансирование. Работа выполнена за счёт гранта Российского научного фонда № 23-16-00220,