Закономерности прохождения стартового отрезка трассы скалолазами высокой квалификации

Актуальность. Эффективность любого спортивного выступления обуславливается множеством влияющих на результат различного рода факторов, и скалолазание не является исключением. В отличие от многих видов спорта (особенно командных видов и единоборств), количество таких факторов в скалолазании невелико (Delignieres и др. 1993; Binney, Cochrane 1999; Bertuzzi и др. 2011; Котченко 2016). Однако их поиск и изучение существенно осложнены специфическими особенностями, неповторимостью и непредсказуемостью современных соревновательных скалолазных трасс. В то же время знание закономерностей поведения, основных компонентов соревновательного процесса (СП) в сложном лазании и умение рационально использовать эти закономерности в ходе выступления на международных соревнованиях, несомненно, способствует максимальной реализации соревновательного потенциала спортсмена.

Следует отметить, что существует достаточно большая группа стохастических, вероятностных факторов: болезни и травмы, проблемы психологического характера, неудачный подбор снаряжения, погодные условия и др. Эти факторы могут проявиться и оказать определенное влияние на результат, но обычно спортсменам высокого класса удается минимизировать их влияние перед ответственными соревнованиями. По этим причинам в теории СП в скалолазании целесообразно изучение таких показателей и компонент, которые всегда присутствуют в ходе прохождения соревновательной трассы.

Анализ выступлений скалолазов на международных соревнованиях показал, что одним из таких важных компонентов является время, затрачиваемое скалолазом на выполнение первых восьми результативных движений (8). По аналогии с беговыми дисциплинами легкой атлетики - это время прохождения стартового отрезка дистанции, фиксируемое по завершении выполнения восьмого перехвата.

Цель исследования - изучить закономерности, связи и получить комплексную оценку степени влияния времени прохождения стартового отрезка трассы на общий итог спортивного выступления.

Организация исследования. В период с 2013 по 2016 гг. анализировались выступления мужчин на полуфинальных и финальных трассах этапов кубка и чемпионатов мира. Общая выборка наблюдений включает 483 индивидуальных старта. Количество соревновательных трасс -41.

На первом этапе исследований изучалась степень связи с результатом для случая, когда в качестве конечной точки стартового отрезка используется не фиксация движения, а заданное время: 30 и 40 секунд. На втором этапе определялось количество движений, имеющее наиболее тесную связь с итогом прохождения трассы: 8, 10 или 12. Третий этап - анализ полученных данных.

Испытуемые — высококвалифицированные спортсмены мирового уровня, специализирующиеся в лазании на трудность.

Методы исследования. При обработке данных применялись методы корреляционного и регрессионного анализа. Используемые программы: Kinovea 0.8.24, Statistika 10.

Обсуждение результатов. На первом этапе исследований было проанализировано 60

индивидуальных стартов, когда в качестве конечной точки стартового отрезка трассы использовалось значение в t = 30 секунд (/зо), и такое же количество стартов, когда t = 40 (/₄₀). Как показал анализ данных, за это время спортсмены успевают сделать в среднем 6,4 (при t^ и 8,3 (при ?4₀) движения. Степень корреляции с результатом составила: г_Й0 = 0,28 при уровне значимости р = 0,032; для г_А0 = 0,29; р = 0,023.

В ходе второго этапа изучались показатели стартового отрезка, когда в качестве критерия использовалось время, а в качестве конечной точки - показатели фиксированного движения: 8 (₈), Ю (ю) и 12 (2). Всего проанализирован 101 старт в каждом варианте. Корреляционный анализ позволил установить, что степень связи с результатом прохождения трассы в этом случае существенно разнится. Так, при значении конечной точки отрезка, равном 10 движениям, коэффициент r_dX0 = -0,10, не является значимым: р = 0,343. При 12 движениях степень корреляции выросла и составила г^г = -0,23; р = 0,020. Но наиболее значимые показатели были выявлены, когда протяженность отрезка составляла 8 движений: r_d% = - 0,31; р = 0,002.

Надежность выбора в качестве конечной точки отрезка показателей движения, а не времени, подтверждается результатами первого этапа исследовании, а его размерность - анализом трех вариантов измерений: dg, d\0 и dn.

Таким образом, в результате первых двух этапов исследований были установлены критерии, определившие выбор восьмого движения (d^), в качестве фактора, оказывающего влияние на эффективность выступления в ходе прохождения стартового отрезка трассы.

Анализ общей группы временных наблюдений фактора (п = 483) позволил получить общие характеристики изучаемого ряда данных (табл. 1).

Степень связи с результатом, присущая большому количеству наблюдений, оказалась несколько меньшей, чем коэффициент корреляции, полученный на предварительном этапе исследований. Тем не менее, расчетное значение находится в установленной зоне поиска, когда г > 0,2, и является высоко значимым: р « 0,001. В ходе исследований удалось выяснить причину снижения степени связи, вызванную попаданием в исходную выборку значительного числа наблюдений, свойственных трассам короткой протяженности (s-трассы).

Закономерности связи ^-фактора с результатом, характерные для общей группы наблюдений, хорошо просматриваются на диаграмме рассеяния (рис. 1).

Таблица 1

Показатели прохождения стартового отрезка, характерные для общей группы соревновательных трасс

Характеристики (и = 483)
Корреляция с результатом	Г	-0,21
Уровень значимости	р	<0,0001
Математическое ожидание	d в	40,5
Минимум	min	16
Максимум	max	81
Стандартное отклонение	<7	12,2

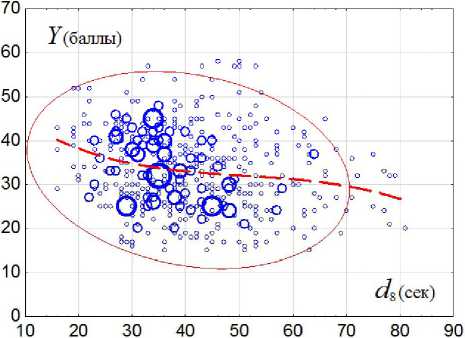
Рис. 1. Диаграмма общего ряда наблюдений фактора восьмого движения

Среднее время прохождения стартового отрезка составляет примерно 40 секунд, но максимальные значения могут достигать 80 и более секунд. Время прохождения стартового участка связано с результатом обратной зависимостью: чем меньше время, тем лучше результат. И несмотря на то, что степень связи находится в низкой зоне, она существует, и вероятность нарушения данной закономерности очень мала: р = 6,4Е-06. Вид связи близок к линейному (рис. 1), поэтому в данном случае проще использовать уравнение линейной связи. Величина стандартной ошибки при этом возрастает незначительно. Связь описывается уравнением:

d_& = 49,6-0,224Y_top, где ds — оптимальное время прохождения стартового участка трассы;

Y_top — протяженность трассы (максимальный судейский балл).

Стандартная ошибка составляет т = 12,0 (29,6%). Это высокий показатель, но, тем не менее, расчетное значение, несомненно, может служить хорошим ориентиром при построении тактического плана выступления.

Рассмотрим пример. Протяженность соревновательной трассы Y_top = 50. Тогда оптимальное время прохождения стартового отрезка составит:

ds = 49,6 - 0,274 * 50 = 36 с.

С учетом возможной ошибки, временной диапазон d₈ для таких трасс может колебаться в пределах 36 ± 10,7 с (от 25 до 47 с). В уравнение можно вводить не максимальный балл (У_ТОр), а заданный результат (У).

Например, если спортсмен понимает, что он не сможет пройти трассу полностью, в уравнение лучше ввести прогнозируемо реальный результат, допустим У = 40. Тогда оптимум d₈ будет несколько большим:

d_% = 49,6 -0,274 * 40 = 39 ± 11,5 с.

Однако не все так просто. Дальнейшие исследования показали, что степень связи фактора с результатом во многом зависит от протяженности соревновательной трассы и ее категории трудности.

Первый важный аспект — протяженность трассы. В качестве критерия используется показатель лидера, или отметка Ytop. В данном анализе трассы были разделены на две группы: короткие (s-трассы), когда Ytop < 42, и среднедлинные трассы (елД-трассы), когда Ytop > 42. Короткие трассы реже встречаются на соревнованиях, и соотношение «s» к «ext» определяется как 1 к 2,4. Динамика изменений значений в зависимости от роста показателя У представлена на рисунках 2, 3.

Выяснилось, что связь с результатом для s-трасс (рис. 2) находится ниже установленной зоны поиска: г = - 0,15, р = 0,066. То есть на коротких трассах время прохождения стартового участка трассы в большинстве случаев не оказывает заметного влияния на общий результат выступления. В то же время на exi-трассах (рис. 3) коэффициент вырастает до г = - 0,36 и становится высокозначимым: р = 5,9Е-11. И это уже достаточно весомый показатель, который нельзя игнорировать.

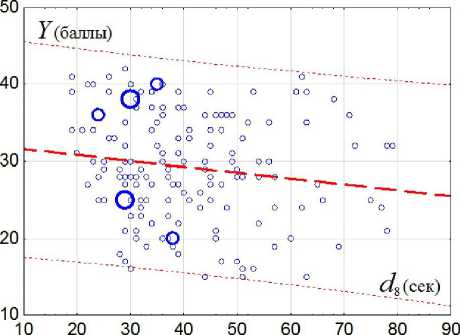
Рис. 2. Динамика изменении показателей «d₈» на s-трассах

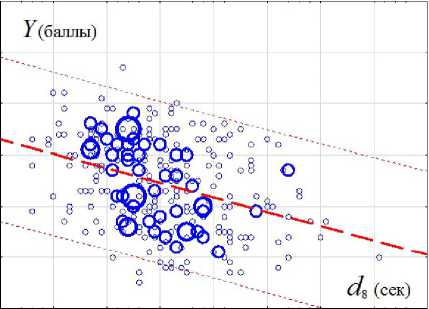
10   20   30   40   50   60   70   80   90

Рис. 3. Динамика изменений показателей «d₈» на елМрассах

Дальнейший анализ показал, что степень связи с результатом на конкретных трассах может достигать существенно более высоких значений. Так, на полуфинальной трассе этапа кубка мира 2014 г., Мокро (Корея), коэффициент корреляции достиг г = - 0,62, р = 0,016. В полуфинале чемпионата мира 2014 г., Gijon (Испания), г = - 0,47, р = 0,022.

На полуфинальной трассе чемпионата 2016 г., Paris (Франция), величина коэффициен- та составила г = - 0,59, р = 0,002, а чех A. Ondra, занявший первое место, сумел пройти стартовый отрезок с лучшим результатом 29 с. Спортсмены D. Skofic и G. Supper, показавшие в полуфинале чемпионата второй и третий результаты, потратили на выполнение первых восьми движений 36 и 32 секунды соответственно. При общей протяженности полуфинальной трассы У,ор = 46 оптимальное время фактора находится в пределах 37 ± 10 с, и продемонстрированные спортсменами показатели четко укладываются в расчетный интервал.

Что касается второго аспекта, определяющего степень связи показателя «d₈» с результатом, - общей категории трудности трассы (или категории стартового участка), соревновательная практика показывает, что предсказать до начала соревнований категорию трудности сложно (Кауров 2015: 12). Но именно сложность стартового отрезка во многом и характеризует исследуемую закономерность.

Этот факт не позволяет с высокой степенью вероятности утверждать, что связь рассматриваемой пары признаков «d8 — У» будет эффективно работать на любой трассе. Как нам уже известно, она наиболее ярко выражена на трассах средней и длинной протяженности, следовательно, если построить уравнения связи для каждой группы трасс, можно существенно снизить величину стандартной ошибки. К при меру, даже в объединенной группе exl-трасс, ст. ошибка снижается с т = 12,0 до т = 10,4. Однако выполнение исследований в этом направлении потребует большого количества наблюдений (по предварительным оценкам, до 1 500). В этой ситуации, с практической точки зрения, несмотря на высокий показатель стандартной ошибки, целесообразно пользоваться полученным общим уравнением связи.

Выводы. Впервые в теории спортивного скалолазания изучены закономерности, характеризующие степень связи результата выступления со временем прохождения стартового отрезка соревновательной трассы. Получены комплексные оценки степени влияния для общей группы наблюдений (г = -0,21; р « 0,001), а также для двух выделенных групп трасс: s-трассы г = -0,15; ехитрассы г = -0,36. Построена формула связи для трасс различной протяженности, позволяющая рассчитать оптимальное время выполнения первых восьми движений на маршрутах высшей категории трудности.

Применение результатов исследований в практике соревновательной деятельности будет способствовать повышению эффективности выступления и максимальной реализации индивидуального потенциала скалолаза.