Закономерности распределения напряжений в грунтовых основаниях внутрихозяйственных автомобильных дорог

Местные автомобильные дороги, расположенные в границах сельских поселений, предназначенные для транспортного обслуживания объектов по производству, переработке и сбыту сельскохозяйственной и иной продукции, а также внутрихозяйственные автомобильные дороги разделяются на две группы: магистральные и полевые. В соответствии с нормативным документом СП 99.13330.2016 при проектировании внутрихозяйственных магистральных дорог должно быть учтено требование по обеспечению круглогодичных транспортных связей с объектами сельскохозяйственной переработки, сельскохозяйственного производства и иного вида производства, а также с объектами социальной инфраструктуры (объекты торговли, культуры и т. п.). Для обеспечения круглогодичного проезда дорожную одежду устраивают из материалов, хорошо сопротивляющихся воздействию транспортных средств и влиянию климатических факторов. Дорожная одежда передает нагрузку от автомобилей на нижележащие слои основания, рассредоточивая ее на большую площадь. Для этих целей эффективным инструментом является армирование конструктивных слоев геосинтетическими материалами, в том числе плоскими георешетками [1; 2]. В результате этого в земляном полотне возникают значительно меньшие напряжения и деформации.

Возникающие в дорожной одежде напряжения от колес автомобилей уменьшаются с глубиной. Процессы, протекающие при деформации грунтового основания, подчиняются общим закономерностям механики грунтов. При этом следует иметь в виду, что форма и площадь контакта, а также распределение давлений зависят от соотношения жесткостей грунта и шины. Для экспериментальной оценки механических свойств и анализа напряженно-деформированного состояния дорожных одежд и грунтовых оснований наиболее широко применяются штамповые испытания с использованием жесткого штампа круглой формы.

Объекты и методы

Рассмотрим задачу определения напряжений в грунтовом основании при действии на него круглого жесткого штампа радиусом R , загруженного сосредоточенной нагрузкой Р . Расчетная схема представлена на рис. 1.

Грунтовые основания, с одной стороны, представляют собой зернистую среду, напряжения в которой определяют, используя математический аппарат механики грунтов. С другой стороны, для определения напряжений в грунтовых основаниях широко используется расчетная модель сплошной среды и математический аппарат теории упругости. В соответствии с теорией упругости давление на упругое полупространство, передаваемое жестким штампом, распределяется по закону квадратичной параболы:

Р

q(r) =----

2nR^R2 — г2

Эпюра давлений (рис. 2) получена в результате точного решения задачи о вдавливании штампа в упругое полупространство. Решение задачи ‒ в цилиндрических координатах. Особенностью данного решения является то, что минимальное давление возникает под центром штампа, а под краем штампа давление бесконечно велико.

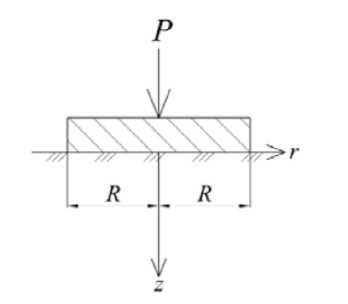
Рис. 1. Расчетная схема

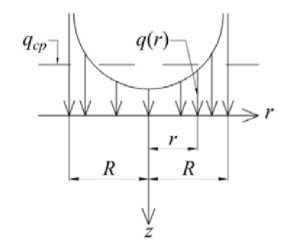
Рис. 2. Распределение давления на основание под жестким штампом

На практике обычно вместо точного закона распределения давления под жестким штампом используют приближенную равномерную зависимость:

_ р

Чср = ^R2'                              (2)

Эпюра давлений в этом случае имеет вид, представленный на рис. 3, а.

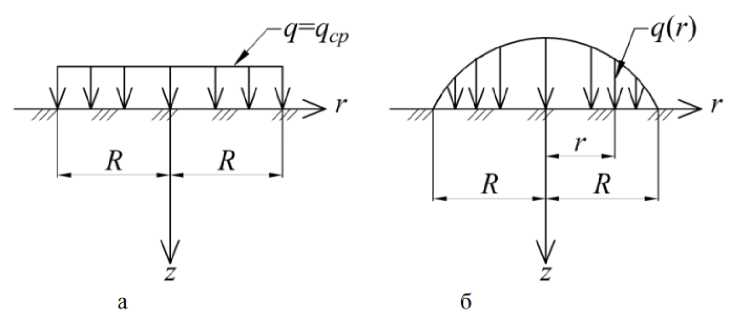
Рис. 3. Распределение давления от жесткого штампа на грунтовое основание: а – равномерное; б – параболическое

Совсем иной вид имеет эпюра давлений на грунтовое основание, установленная экспериментально Фарбером [3] при надавливании круглым жестким штампом на основание из песка. Закономерность распределения давления под штампом имеет вид квадратичной параболы (3) и представлена на рис. 3, б:

Ч(г) = 2ч(1-^).

Определение напряжений по формулам теории упругости

Рассмотрим основные формулы теории упругости для вычисления главных вертикальных напряжений o_z под штампом в точках, расположенных по оси Z :

решение Буссинеска для случая равномерного распределения нагрузки [4]:

° = ^(1—[1+(R)]  );

решение С.П. Тимошенко [5] для произвольного закона распределения нагрузки q(r) :

к

oz = J 3q(r) ■ rz3(r2 + z2)-5/2dr;

о

Для постоянной нагрузки q (г) = q выражение (5) после интегрирования принимает вид

о = q [—

zL + (R2+z2

)3/2]'

Для параболической нагрузки (3) выражение (5) после интегрирования будет иметь вид

2qz3 [2z3(R2 + z2) + (R2 + z2)1'5 ■

°z = R2 [

z3(R2 +z2)1'5

(R2

—

2z2)

-----].       (7)

В работе американского профессора Роя Олсона [3] приведены формулы для определения напряжений под штампом в точках, расположенных на оси Z, при равномерном распределении нагрузки:

ап

z q(1   (1 + а2)п/2)

и при параболическом распределении

Oz = 2q [1 + -

—

— ■ а2 — п

2 — n

2—n

■ ап • (1 + а2) n I, (9)

где а - переменная, определяется по формуле

z

“ R’

На рис. 4 приведены экспериментально установленные данные о распределении напряжений под штампом, теоретически вычисленные по формулам (8) и (9).

При сравнении кривых распределения напряжений по глубине, вычисленных по формулам (4) и (7), оказалось, что формула (7) соответствует параболическому распределению (9) при n = 3, а решение

Буссинеска (4) - равномерному распределению (8) при n = 3.

Помимо формул теории упругости для определения напряжений в грунтовом основании как в сплошной среде имеется альтернативный подход. Он заключается в использовании математического аппарата механики грунтов. Рассматривая грунтовые основания как зернистую среду, Кандауров [6] предложил использовать следующие формулы для вычисления напряжений:

^Ч-'Ч-У]’

^z = 2q- {1 -

2vz2 R2

^Ч-УВ'

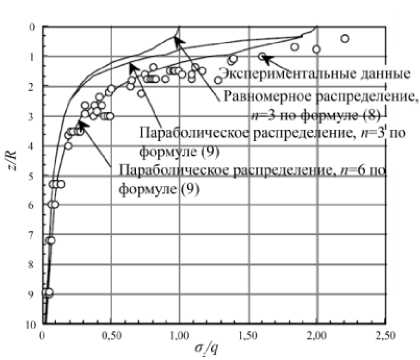
Рис. 4. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (8) и (9) [3]

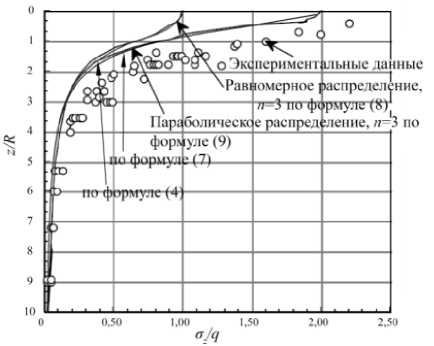
Рис. 5. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (4), (7), (8) и (9)

В механике грунтов основными механическими характеристиками, влияющими на распределение напряжений, являются угол внутреннего трения грунта ф и коэффициент бокового давления v . В табл. 1 приведены нормативные значения угла ф для некоторых грунтов [7]. Видно, что угол ф изменяется в пределах от 18 до 38 ° .

Таблица 1

Нормативные значения ф

Вид грунтa	Разновидность	Ф , град.
Песок	Крупный и гравелистый	38
	Средней крупности	35
	Мелкий	32
	Пылеватый	30
Глинистые грунты	Супесь	27
	Суглинок	22

	Глина                              18
Скальные грунты	Известняк                          33 Туффиты и филлиты               28 Порфиры                        37

Г.И. Покровский, пользуясь методами статистической механики, установил связь между коэффициентом бокового давления 11 и углом внутреннего трения ф сыпучего тела:

11 = 1 — 0,74 • tan ф.                     (13)

В случае очень деформируемых обойм коэффициент бокового давления

172 очень близок к расчетному и определяется по формуле, предложенной Ренкиным:

1 — sin ф In = --------

.

1 + sin ф

В случае жесткой обоймы коэффициент бокового давления ν3 рассчитывается по формуле, предложенной Жаки:

v3 = 1 — sin ф.

В табл. 2 приведены вычисленные по формулам (13)–(15) значения коэффициентов бокового давления 1 1 , 17 2 , 17 ₃ .

В соответствии с материалами монографии Г.К. Клейна [8] коэффициенты бокового давления для различных грунтов принимают значения, приведенные в табл. 3.

Таблица 2

Коэффициенты бокового давления, вычисленные по формулам (13) – (15)

ф , град.	38	35	32	30	27	22	18	33	28	37
171	0,42	0,48	0,54	0,57	0,62	0,70	0,76	0,52	0,61	0,44

V 2	0,24	0,27	0,31	0,33	0,38	0,45	0,53	0,29	0,36	0,25
v 3	0,38	0,43	0,47	0,50	0,55	0,63	0,69	0,46	0,53	0,40

Сравнение формул Кандаурова (11),  (12) при v =  0,42 с экспериментальными данными показано на рис. 6. Из представленных графиков видно, что формула (12) соответствует параболическому распределению (9) при и = 3.

Результаты и их обсуждение

Метод экспоненциальной аппроксимации широко используется в дорожном строительстве. Например, в работах [9], [10] использована экспоненциальная зависимость в виде

Gz = В • exp(-yz),                     (16)

где В - константа, v 1 - коэффициент затухания по глубине.

В данной работе предлагается вместо выражения (16) использовать следующую зависимость для определения напряжений в точках, расположенных на глубине z:

Gz = 2q[exp(v{1 - yiz})](1-v),                (17)

где v - коэффициент бокового давления грунта; у 1 - коэффициент затухания, определяемый по результатам экспериментальных исследований.

Таблица 3

Коэффициенты бокового давления для типичных грунтов

Грунт	Коэффициент бокового давления ν для грунтов
	сухого	влажного	насыщенного
Пески	0,40	0,45	0,45
Суглинки	0,50	0,55	0,60
Глины	0,60	0,70	0,70

Таблица 4

Значения v и y_t

v	0,2	0,3	0,4	0,5	0,6	0,7	0,8
П	23	19,15	17,1	16,5	17,1	19,15	24

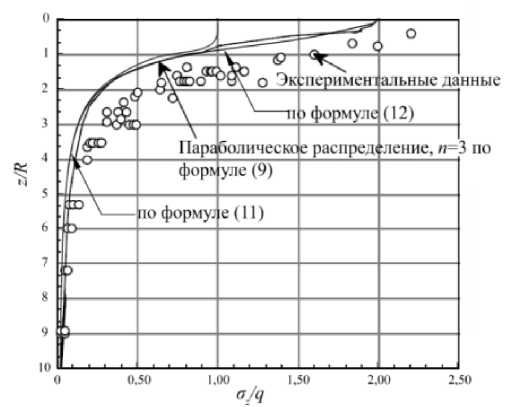
Рис. 6. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (9), (11) и (12)

В табл. 4 представлены значения у 1 , вычисленные при различных значениях коэффициента бокового давления v , изменяющегося в пределах от 0,2 до 0,8. Зависимости распределения напряжений o_z по глубине, полученные в соответствии с формулами (16) и (17), представлены на рис.

7. Таким образом, имеется несколько формул для определения напряжений по оси симметрии жесткого штампа. Расчеты по этим формулам приближаются к экспериментальным данным, но все же дают заниженные значения напряжений на определенных глубинах. Экспоненциальная аппроксимация по формуле (16) также дает заниженные значения напряжений, поэтому эпюра напряжений имеет недостаточную выпуклость на интервале 0 < z/^ < 4. Наилучшее совпадение с результатами эксперимента для песчаного основания демонстрирует экспоненциальная зависимость (17), в которой вместо одного коэффициента затухания по глубине использованы две постоянные: коэффициент бокового давления грунта v = 0,5 и экспериментально установленный для данного грунта коэффициент затухания у1 = 16,5.

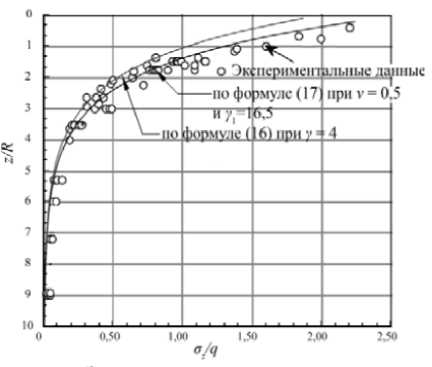
Рис. 7. Экспериментальное и теоретическое распределение напряжений под штампом в соответствии с формулами (16) и (17)

Заключение

В настоящей работе предложена экспоненциальная зависимость изменения по глубине напряжений в грунтовом основании под жестким штампом. Отличительной особенностью данной зависимости является то, что вместо одного коэффициента затухания по глубине использованы две постоянные: коэффициент бокового давления грунта и экспериментально установленная для данного грунта константа. Использование предложенной зависимости позволяет более точно описывать напряженное состояние грунтовых оснований автомобильных дорог и применять для проектирования и конструирования дорожных одежд как внутрихозяйственного назначения, так и общего пользования.