Закономерности роста чистых древостоев березы плосколистной (Betula platyphylla)

Введение. В последние десятилетия площадь лесов Дальневосточного федерального округа (ДФО), в которых преобладает береза плосколистная (Betula platyphylla), увеличивается высокими темпами. Так, за период с 2003 по 2009 г. указанный показатель вырос на 2,8 % [1]. Вызвано это, в первую очередь, изменением климата в регионе. Тем не менее особенности роста белоберезников до сих пор не нашли отражения в научной литературе. В то же время лесная промышленность региона традиционно приурочена к лесосырьевым базам, сформированным хвойными породами. С практической точки зрения это может привести к дефициту сырья, убыткам лесопромышленного комплекса, сокращению рабочих мест. Рациональное использование лесных ресурсов, качественные показатели которых претерпевают существенные изменения за короткий отрезок времени, определяется наличием нормативной базы, отражающей комплексную продуктивность древостоев. Для её разработки необходимо изучить региональные особенности роста белоберез-ников.

Цель исследований . Изучение особенностей роста чистых белоберезников на основе массового экспериментального материала – повыдельной базы данных лесоустройства.

Объекты и методы исследований. Географическими границами объекта исследований является Чумиканский лесохозяйственный район [2]. Указанные данные охватывают леса, в которых береза плосколистная представлена пятью и более единицами в составе, произрастающими в первом ярусе – генеральная совокупность данных в количестве 4793 выделов. Выборка представляет собой чистые белоберезники (10 единиц в составе) в количестве 949 выделов.

В работе изучены особенности роста белоберезников на основе информации о высоте, достигнутой к определенному возрасту.

Прежде чем строить линии роста, экспериментальный материал был подвергнут фильтрации следующим образом. Для каждого класса возраста рассчитывались средние высоты и их статистики. Затем те наблюдения, значения которых превышали по модулю 1, 96 δ (стандартное отклонение от среднего), удалялись. В результате количество наблюдений сократилось до 907. Далее для каждого класса возраста рассчитывались средние значения высоты. Полученные средние высоты выравнивались аналитически функцией Митчерлиха (1):

у : a(i - exp(-bxS) , (1)

где у – значение таксационного показателя; х – класс возраста; a, b, c – параметры уравнения.

По классификации А.К. Кивисте [4], функция (1), известная как функция Дракина-Вуевского, отвечая общим требованиям к функциям роста, имеет формулу вычисления точки перегиба, рекомендуется в качестве базовой при моделировании хода роста по основным таксационным признакам.

Для определения границ поля наблюдений в каждом классе возраста выделялись максимальные и минимальные средние высоты, которые подвергались аналитическому выравниванию функцией (1). В результате были получены верхняя и нижняя границы поля экспериментальных данных. Наблюдения, значения которых находились за пределами границ, были удалены. Количество наблюдений составило 795 выде-лов. Указанные наблюдения явились основой для построения кривых хода роста в высоту. Основные статистики распределения средних высот по классам возраста приведены в табл. 1.

Основные статистики распределения средних высот по классам возраста

Таблица 1

Класс возраста	10	20	30	40	50	60	70	80
Среднее	2,71	6,20	9,90	12,10	14,83	17,19	18,73	19,73
Стандартное отклонение	0,72	1,61	1,45	1,72	1,23	1,48	0,94	1,10
Коэффициент вариации, %	26,4	25,9	14,6	14,2	8,3	8,6	5,0	5,6
Эксцесс	-0,87	-1,02	-0,79	-1,24	-0,19	-0,46	-0,75	-0,92
Асимметричность	0,50	0,35	-0,20	0,19	0,13	-0,49	-0,16	-0,44
Число наблюдений	41	82	146	122	63	53	22	11

Изменчивость средней высоты в пределах класса возраста не превышает 27 %. Таким образом, на 5%-м уровне значимости были получены три кривые изменения высот с возрастом белоберезников, которые приняты нами за границы классов роста, характеризующие древостои с максимальными значениями высот (H max ), средними значениями (H sred ) и минимальными значениями высот (H min ). Параметры уравнения и показатели адекватности приведены в табл. 2.

Результаты аналитической аппроксимации средних высот

Таблица 2

Ряд	Параметр уравнения			S	R
	A	B	C
H max	22,722	0,039	1,489	1,351	0,980
H sred	23,949	0,026	1,461	1,476	0,943
H min	30,524	0,015	1,574	1,135	0,981

Примечание. Hmax, Hsred, Hmin – ряды изменения средней высоты, полученные по максимальным, средним и минимальным средним высотам; S – стандартная ошибка; R – коэффициент корреляции.

Параметр «а» характеризует предельное значение таксационного признака. Данные табл. 2 позволяют сделать предположение о существовании связи скорости роста с абсолютными значениями таксационного признака – с увеличением скорости роста предельное значение высоты снижается. Для определения характера указанной связи на основе полученных рядов изменения высоты с возрастом определялась скорость изменения высоты по формуле (2), где Y' – скорость изменения таксационного показателя; у – значение таксационного показателя; a, b, c – параметры уравнения.

Y = b • c • y

Г a ^

1 c

— 1

< У J

Дополнительно определялся возраст точки перегиба (3). Соответствующая этому возрасту высота рассчитывалась по функции (1) с учетом параметров табл. 2.

ln(C )

t max = ——. b

Результаты расчетов отражены на графике рис. 1.

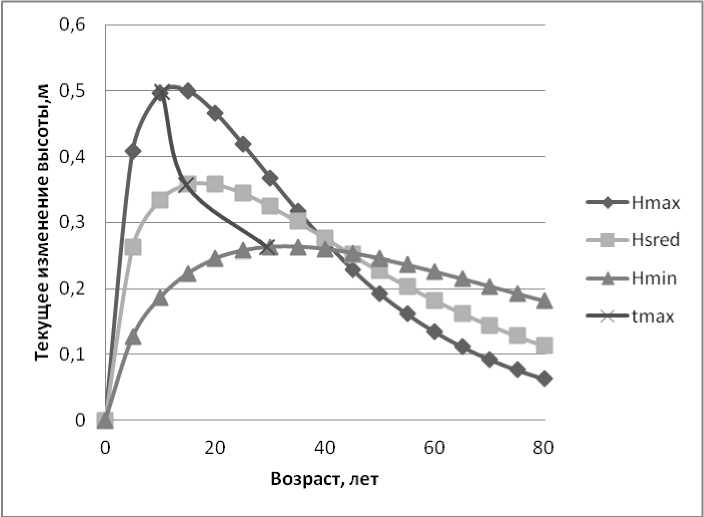
Рис. 1. Скорость изменения высоты с возрастом: Hmax, Hsred, Hmin – ряды изменения средней высоты; tmax – максимальное изменение средней высоты

Результаты исследований и их обсуждение. Данные рис. 1 свидетельствуют, что у чистых белобе-резников Чумиканского ЛХР возраст кульминации текущего изменения средней высоты варьируется от 10 до 29 лет. При этом точки экстремумов от максимального значения к минимальному плавно снижаются по параболической кривой. В возрастном интервале 41–45 лет для всех классов роста скорость изменения средней высоты можно принять практически одинаковой. С биологической точки зрения в насаждениях различных условий произрастания на генетическом уровне заложено стремление к достижению климаксового состояния – равновесия [3], которого они достигают, затратив различное количество энергии. Различия затраченной энергии объясняется тем, что в древостоях часть энергии тратится на преодоление сложных условий произрастания. К тому же этот процесс занимает некоторое время. Данный аспект необходимо учитывать при назначении лесохозяйственных мероприятий, проводя уход в первую очередь в насаждениях, произрастающих в худших условиях. Указанная тенденция согласуется с определением биологической системы (в том числе древостой) с позиции термодинамики, согласно которой биологическая система является открытой неравновесной системой, непрерывно обменивающейся энтропией с внешней средой [5, 6, 7]. С практической точки зрения в интервале 45 лет можно осуществлять бонитирование древостоев, поскольку они исчерпали биологические и экологические возможности определенных условий произрастания.

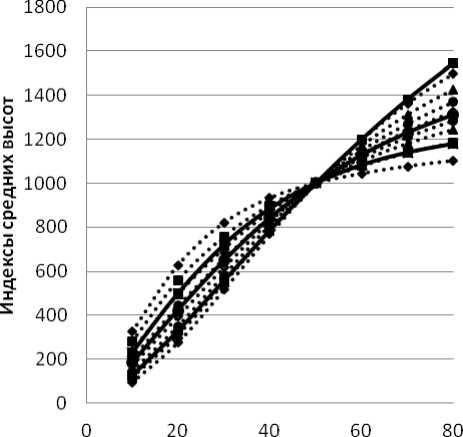
Полученные классы роста изменения средних высот с возрастом сравнивались с типами роста березовых древостоев по Н.Я. Саликову [8]. Для этого абсолютные значения средних высот методом индексов, приняв за базу 50-летний возраст, были преобразованы в относительные. На рис. 2 показаны индексные значения высот белоберезников Чумиканского ЛХР. Следует отметить, что характер роста в высоту чистых белоберезников Чумиканского ЛХР в относительных величинах занимает достаточно узкий диапазон. Другими словами, характеризует близкие лесорастительные условия произрастания древостоев.

Возраст, лет

....... 1

• • ••»•• 2

• • ••*•• з

....... 4

• • ••♦••• 5

• • ••*•• 6

...*... 7

• •    ••♦••• 8

• ■    Hmax

—•— Hsred

• ■    Hmin

Рис. 2. Сравнение построенных рядов с типами роста березовых древостоев по Н.Я. Саликову

В типовой шкале роста Н.Я. Саликова построенные ряды соответствуют индексам от 3 до 7 типов роста. Характерной особенностью изучаемых белоберезников является переход из одного типа роста в другой. Так, ряд индексов h-max, отражающий верхний придел роста белоберезников, из 3 типа роста переходит во 2, Ряд h-min – из 7 типа роста – за пределы 8 типа. Такие изменения, во-первых, вызваны особенностью методики построения абсолютных высот, во-вторых, морфометрическими характеристиками березовых древостоев Чумиканского ЛХР. Последние отражают динамику таксационных показателей модальных древостоев, а при составлении типовой шкалы Н.Я. Саликова участвовали в основном нормальные насаждения, которые и представляют систему типов роста.

Выводы

Таким образом, проведенные исследования в чистых насаждениях березы плосколистной Чумикан-ского ЛХР позволяют сделать следующие выводы .

Система типов роста Н.Я. Саликова учитывает многообразие характеров роста древостоев и позволяет сравнивать определенные таксационные признаки насаждений независимо от географических условий произрастания.

Особенности роста белоберезников Чумиканского ЛХР по высоте соответствуют границам типовой шкалы роста Н.Я. Саликова. Вместе с тем изучаемый таксационный признак, начиная расти по одному типу, не сохраняет постоянство в более старшем возрасте и переходит из одного типа роста в другой, что указывает на особенности лесообразовательных процессов, протекающих в северной части ареала распространения породы.

В процессе роста белоберезников наступает возрастной период, в котором скорость изменения высоты характерна для всего семейства кривых – линии пересекаются примерно в одном возрасте (41–45 лет). Указанный период с практической точки зрения можно приравнять к возрасту рубки, а с биологической – к началу распада древостоя.

Использование функции Митчерлиха позволило определить максимальную скорость изменения таксационного признака во времени и пространстве.