Закономерности термообработки вязких продуктов в пластинчатом скребковом аппарате
Автор: Рашкин К.А.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Процессы и аппараты пищевых производств
Статья в выпуске: 2 (52), 2012 года.
Бесплатный доступ
Описывается конструкция используемых в настоящее время в промышленности скребковых теплообменных аппаратов пластинчатого типа и схема движения продукта в нем. Приводится расчетная схема, ставится и решается задача по аналитическому определению необходимой площади поверхности теплообмена с применением дифференциальных уравнений теплопереноса в движущихся жидких средах, записанных в цилиндрической системе координат при осесимметричном распределении температур.
Теплообмен, скребковые теплообменники, аналитическое исследование
Короткий адрес: https://sciup.org/14039842
IDR: 14039842 | УДК: 66.045(045)
Текст научной статьи Закономерности термообработки вязких продуктов в пластинчатом скребковом аппарате
Пластинчатые скребковые аппараты широко используются для термообработки вязких пищевых продуктов. Закономерности термообработки были изучены в пластинчатом аппарате скребкового типа.
Рис. 1. Основные детали теплообменного элемента: 1 – сварная теплообменная пластина; 2 – уплотнительное кольцо; 3 – нож-мешалка
Основной частью скребкового аппарата является теплообменный элемент (рис. 1). Он представляет собой конструкцию из двух соосных сварных теплообменных пластин 1 вместе с лопастным ножом-мешалкой 3.
Набор последовательно соединенных теплообменных элементов образует теплопередающую поверхность аппарата для нагревания или охлаждения высоковязкого продукта. Внутри охлаждающего элемента поток продукта принудительно закручивается с помощью крестообразных вращающихся лопастей ножа-мешалки, захватывающих практически все пространство между дисками.
Продукт поступает в пространство между дисками как из центрального отверстия, так и из отверстий, расположенных на периферии дисков. При этом лопасти могут вращаться как по отношению к неподвижным дискам, так и совместно с одним из дисков по отношению к другому неподвижному диску.
Траектория течения продукта внутри теплообменного элемента сложная. В связи с этим изучение распределения температуры продукта в теплообменном элементе проведено на основе дифференциальных уравнений теплопереноса в движущихся жидких средах.
показана на рис. 2.
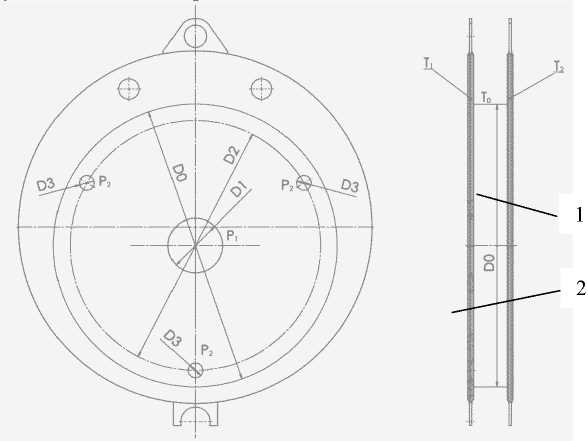
Рис. 2. Расчетная схема: 1 - теплообменные пластины; 2 - продукт; D0 - размер, ограничивающий продуктовую зону; D1 - диаметр входного отверстия; D2 - диаметр, на котором расположены выходные отверстия; Р 1 -давление продукта на входе в теплообменный элемент; Р2 - давление продукта на выходе из теплообменного элемента; T 0 - температура продукта; Т 1 - температура пластины 1; Т 2 - температура пластины 2
Для определения радиальной скорости воспользуемся дифференциальным уравнением стационарного осесимметричного течения несжимаемой вязкой жидкости, полагая в нем коэффициент вязкости µ и плотность продукта ρ не зависящими от температуры для данной пары дисков (охлаждающего элемента)
- L +1 др = r р д r
Данные уравнения записаны для цилиндрической системы координат при осесимметричном распределении температуры без учета диссипации энергии дT дT (д2 T 1 дT д2 T)
vr + vz= a\ 2- ++ 2- I, дr дz l дr2 r дr dz2 )
где T – температура в точках продукта, оС; r, z – цилиндрические координаты точки продукта;
vr , vz - проекции скорости точек продукта на оси r, z ; а – коэффициент температуропроводности, м 2 /с.
Полагаем, что осевая скорость продукта vz значительно меньше радиальной vr и окружной vL скоростей, поэтому в уравнении
(1) положим
определения течении в
д T v — ~ о. Расчетная схема для z дz температуры продукта при его продуктовых каналах аппарата где p – давление в точках продукта, Па; ν -коэффициент кинематической продукта, м2/с, равный
Ц v = —.
Р
Учитывая принудительное продукта, примем, что его угловая вязкости вращение скорость
равна угловой скорости to вращения лопастей, т. е.
д2 v 1 д vr д2 v, г + - + r д r2 r д r дz2
-
vr
,(2)
v L « to r .
В силу этого два слагаемых в левой части уравнения (2) можно представить в следующем
искомых функций. Решив эти уравнения,
найдем
виде: 2
- v^. + 1 d p = 1 d P , (4)
r p 9r p dr где Р - модифицированное давление, Па.
Модифицированное давление
У ( z ) =
^ ( z ) =
P i - P 2
R , u ln—
R 2
P 1 In R 2 — P 2 In R1
представляет разность между истинным давлением продукта и давлением, которое было бы в нем только при его вращении с угловой скоростью [1]. Оно равно
P = p - 2 pro 2 r 2 .
R ln 1
R 2
На основании (10) выражение для модифицированного давления (8) запишем в
виде
При условии постоянства расхода продукта через любое цилиндрическое сечение пространства между пластинами теплопередающего элемента будем искать решение уравнения (2) в виде vr = 1 f (z ). (5)
r
_ , г _ . г
P ln-- P , ln —
1 R 2 R
P = 2 1
R ln 1
.
R 2
Найдем двукратным интегрированием по z функцию f ( z ) из (6) с учетом (7) и (10)
Подстановка выражений (4) и (5) в (2) с учетом (3) дает
1 d P 1 /■„/ \
= -f ( z ) , (6)
U d r r
f ( z ) = P — P-U ln R^ k
R 2
\
z _ + C z + c , (ii) 12
. 7
где двумя штрихами обозначена вторая
производная по координате z .
Чтобы дифференциальное уравнение (6)
имело решение нужно
1 | P = 1 ^ ( z ) . (7)
U 8 r r
Интегрируя левую и правую части равенства (7) по координате r , получим для модифицированного давления выражение
P = ( u ln r > ( z ) + < ( z ) . (8)
Для определения произвольных функций y ( z ) и ^ ( z ) воспользуемся граничными
где C1 , C2 - постоянные интегрирования, которые находятся на основании (5) из условия прилипания продукта к стенкам дисков z = 0, Vr(r,0) = 0, f (0) = 0; , (i2) z = h, Vr (r, h ) = 0, f (h ) = 0 ’ где h – расстояние между дисками. Подставив в равенство (11) граничные условия (12), найдем
C =— h , C = 0. (i3)
Наконец, на основании (11) и (13) выражение радиальной скорости (5) примет вид
условиями
r = R 1 , P = P i ;
r = R 2 , P = P 2 ,
„ = -Ti^ P 2_ 1(z2. r 2 u ln R i r (
R 2
Выразим радиальную секундный расход продукта
скорость через q , используя
где Р 1 – модифицированное давление на входе продукта в междудисковое пространство; Р 2 – модифицированное давление на выходе продукта. Эти давления равны
P = p i — 2 p® R i ,
формулу для расхода q = 2^rjv dz • Подставив 0r сюда выражение vr из (14) и интегрируя его по
P2 = p 2 2 P® R 2 ’
где р 1 , р 2 – истинные давления продукта во входном и выходном сечениях.
Подставив граничные условия (9) в равенство (8), получим систему двух алгебраических уравнений относительно
координате z , находим
P — P 2 _ 3 q . (i5)
------— —--—
2 u ln R i n h
R 2
Таким образом, с учетом (15) выражение радиальной скорости (14) примет вид
vr
3 q 1
n h 3 r
Перейдем к определению температуры в т 5 T л продукте по уравнению (1) с учетом v —® 0.
z d z
Для этого подставим в левую часть данного уравнения выражение радиальной скорости из (14) или (15) и разделим его левую и правую части на коэффициент температуропроводности а . После этого получим
--^ 1 ( z — hz )T =
2ца In R r r
R 2
d 2 t 1 e t e2 t
+1 . d r 2 r dr 8z 2
Поскольку точного аналитического решения данного уравнения получить нельзя, воспользуемся приближенным решением, заключающимся в частичном осреднении его конвективной части по области течения и использовании метода последовательных приближений. Для этого в левой равенства (16) положим
P - P 2
R
2 ц a ln—L
R 2
1 ( 2 2 — hz )f ” r /5 r
1 d T 1 » P i - P 2 ( z 2 r 8 r h oi , R '
0 2 ц а ln—1 R 2
- hz ) dz =
=-< P z P E .1 ”.
n , R r 8 r
12 ц а ln—1 R 2
Введем обозначение
. ( P - P 2 ) h 2
A =- R
12 ц а In —
R 2
или с учетом (15)
A = -
2 nha части
(18 * )
В дальнейшем для практических расчетов будем использовать формулу (18 * ), поскольку расход продукта может быть определен гораздо точнее, чем разность модифицированных давлений, т.к. в эту разность войдут потери давления на различные вредные сопротивления.
Подстановкой соотношения (17) с учетом (18) или (18 * ) в левую часть уравнения (16)
придем к однородному уравнению теплопроводности d T+1 dT(1 - A)+^L = 0. (19)
6r 2 r dr dz 2
Данное уравнение решаем при следующих граничных условиях:
r = R 1 , T = T^ z = 0, T = T 3 , z = h , T = T 4
где T3 и T4 - температура продукта на стенках дисков.
Решение линейного уравнения (19) найдем методом разделения переменных, добавив к его общему решению частное решение специального вида. Для этого положим T ( r , z ) = R ( r ) . Z ( z ) + T 3 + z ( T 4 - T 3 ) . (21)
h
Подстановкой этого выражения T в (17) и разделением переменных получим для функций R ( r ) и Z ( z ) обыкновенные дифференциальные уравнения
Z " + Я2 Z = 0, (22)
rR " + R ' ( 1 - A ) - Я rR = 0. (23) где Я2 - константа разделения.
Решение уравнения (22) имеет вид
Z ( z ) = C 1 cos Я z + C 2 sin Я z . (24)
В силу двух последних граничных условий (20) и выражения (21) функция Z ( z ) должна обращаться в ноль при z = 0 и z = h . Отсюда следует
C = 0, Я = — , k = 1,2,...® ,(25) h т. е. общее решение уравнения (19) будет представлено рядом Фурье по синусам.
Уравнение (23) является уравнением Бесселя произвольного порядка, зависящего от константы А . Поскольку такие функции не табулированы, то дальше будем решать уравнение (19) методом последовательных приближений. Для этого проведем оценку порядка слагаемых в этом уравнении, приведя его к безразмерному виду. Напишем соотношения между размерными и безразмерными величинами
T = T0 T', r = R0 r', z = hz', где T0 - характерная размерная величина искомой функции; T' - безразмерная искомая функция; r - безразмерная радиальная координата; R 0 - характерный радиальный размер; z' - безразмерная осевая координата. В качестве характерной осевой координаты взято расстояние h между дисками.
Перейдя в уравнении (19) к безразмерным величинам, получим h2 d2T' (1- A)h2 j_ dT' ё2Г_ R2 Ir'2"+ R2 r7 "ёй ^"dz^
Таким образом, в безразмерном уравнении (26) порядки слагаемых будут определяться только порядками коэффициентов в этих слагаемых. Для оценки порядка этих коэффициентов примем следующие порядки конструктивных параметров охладителя и обрабатываемого продукта:
h ~0,01м , R 1~0,01м , R 2~0,1м ,
- Т 3 - z ( Т 4 - Т 3 ) = h
да
Z С к в
к 2 п 2 2
R
2 Ah 2 1
к =1
■ к п sin z.
h
Используя формулу для определения коэффициентов ряда Фурье на интервале 0 < z < h , найдем
q ~ 10 4 м 3 / c, ^ ~ 1 Па ■ с, a ~ 10 6 м2/c.
Коэффициент А во втором слагаемом, согласно (18 * ) будет иметь порядок 10 4 , т. е. А >>1. Коэффициент в последнем слагаемом уравнения (26) имеет порядок 1. Принимая во 22
внимание, что h << Ah ~ 1 , оставим в R 02 R 02
уравнении (26), а значит и в уравнении (19) два последних слагаемых. На этом основании уравнение (19) для нулевого приближения при условии А >>1 примет вид
к 2 п 2 Л2
R
2 2 Ah 2 1 (32)
C, =— Т - T - Т - Тл cos к п в Л ' к к п L 1 3 И 4/ J
Таким образом, распределение
Решим
разделения решение в
A d Т
r dr
a2 т n
+— =o o . d z 2
уравнение переменных,
методом
представив его
виде (21). После разделения
переменных для функций R ( r ) и Z ( z ) получим обыкновенные дифференциальные уравнения
R*
R
я2
Ar,
и (22), решением которого будет функция (24) при значениях констант (25). Решение уравнения первого порядка с разделяющимися переменными (28) запишем в виде
- ^L r 2
R ( r ) = C з в 2 A ,
где С 3 - постоянная интегрирования. Таким образом, на основании (21), (24), (25) и (29) получим решение уравнения (27) в виде ряда
к 2 п 2
X
T ( r , z ) = Z С к в 2 Ah к =1
■ кп .
sin— z + h
+ Т з + z ( T 4 - T 3 ) , h
где С к = С 2 С 3 и индекс к показывает, что эта константа будет зависеть от номера к собственных чисел Я из (25).
Найдем постоянные интегрирования Ск , используя первое граничное условие (20), т. е. Т ( R 1 , z ) = Т 1 . На основании этого условия и соотношения (30) получим уравнение для определения Ск :
температуры в пространстве между дисками в нулевом приближении на основании (30) и (32) примет следующий вид:
1 ( R 2 - r 2 )
2 " ГЕ Т - Т 3 - ( Т 1 - Т 4 ) cos к п ] в 2 Ah х
Т ( r , z ) = -Z - ' "
к * xsin —2 + Т + z(T 4 - T ).
h 3 h ( 43 )
Для нахождения первого приближения решения уравнения (24) подставим найденное решение нулевого приближения в ранее отброшенное слагаемое d 2 T этого уравнения.
d r2
После этого придем к неоднородному линейному уравнению в частных производных:
A 8T d 2 T
1= r dr d z z"
2п «V T - T 3 - ( T 1 - T 4 )'
—2 Z к
Ah к = 1 cos кп
2 2 x k^ 2 2,
1 к п 2 I 2 A hRR 1 r ) ■ кп
1-- r re 2 A h sin— z .(33)
Ah 2 J h
Будем искать решение этого уравнения в таком же виде, как и решение уравнения (27) нулевого приближения, т. е.
T ( r , z ) =
« z (34)
= Z Fk ( r ) sin --z + T 3 - -( T 3 - T 4 ) , к = 1 h h
где f- ( r ) - неизвестная пока функция,
зависящая от координаты r и номера к собственных чисел Я из (25). Подстановкой выражения т ( r , z ) из (34) в левую часть уравнения (33) и приравниванием коэффициентов при sin k п z в левой и правой h
частях уравнения (33) получим обыкновенное линейное уравнение первого порядка относительно функции F ( r ) .
A dF, k 2 n 2 „
' Fk rdr h2
с * = - k | T - T 3 - ( T - T 4 ) cos k n ] x
= - Ah [ T — T — ( T — T 4 ) cos k n ]x
x
+ R i
k n 4
R
A k 2 n l R 2 e 2 Ah 2
.
x
1 -
k П2
Ah 2
k n 2
2 I Ph?R1- r ) r I e
Решением этого уравнения является функция
Fk ( r ) = -S[ T - T 3 - ( T i - T 4 ) cos k n ]x
Подставив данное выражение С к в правую часть равенства (36), приведем его к виду
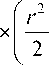
k n 4
4 Ah 2
k 2 n 2 , „2 2,
k 2 П 2 2 r + C * e 2Ah 2
T ( r. z ) = тг ” f -iT к2 тт2 A2 h2 1
= - -272 Z 1 k I T i - T 3 - ( T i - T 4 ) cos kn 1 r 2 - R 2 - --^ ( r 2 - R i4 ) - lx
A h k = 1 I ^ 2 Ah k n ]
+ T 3 - z ( T 3 - T 4 ) - (37)
h
k 2 П 2 (П2 r2 x e "A^ ( R 1 - r
. kn sin z h
C *
k
- постоянная интегрирования.
На основании (34) и (35) имеем
П
T ( r > z ) = - ДТ^ 1 k [ T - T 3 - ( T - T 4 ) cos k n ]|
w
A 2 h 2 k = 1
- k 2 П 2 r 2 1
+ C * e 2 Ah2r [ sin k n z + T 3 - z ( T 3 - T 4 ) . I h h
1 k n 41 • 'rr 4 e'
2 Ah 2 1
k 2 » 2 ,„2 j, , 2 A ?( R 1 - r )
Постоянную интегрирования C k * находим так
же,
как
и
постоянную
С к
для нулевого
приближения, т. е. из условия T ( R 1, z ) = T 1.
Точно так же, как и в равенстве (31), получим разложение функции, стоящей в левой части этого равенства в ряд Фурье по синусам. Из формулы для определения коэффициентов этого
ряда находим:
+
Формула (37) представляет решение уравнения (19) при граничных условиях (20) в первом приближении. Эта формула может быть применена для расчета температуры продукта как при центральном, так и при периферийном способе подачи в пространство между дисками. В первом случае R 1 < R 2 , P1 > P2 , а во втором случае наоборот R 1 > R 2 , P 1 < P 2 .


