Законы сохранения в задаче о продольной плоской волне нагрузки в упругопластическом стержне

1. Рассмотрим процесс распространения пластических деформаций в полубесконечном упругопластическом стержне, вызванных приложенной к концу стержня динамической нагрузкой p ( t ), не убывающей во времени (т. е. dp / dt ≥ 0). Проведем решение в лагранжевой системе координат: за ось х возьмем ось стержня, начало координат х = 0 выберем на левом конце стержня. Предположим, что в процессе деформации не происходит бокового выпучивания стержня и что влияние поперечных деформаций стержня на процесс распространения продольных волн пренебрежимо мало. Рассмотрим малые деформации стержня и будем предполагать, что плотность стержня в процессе деформирования не изменяется. Единственной отличной от нуля составляющей тензора напряжений будет σ _xx =σ , отличными от нуля составляющими тензора деформаций будут ε _xx =ε и ε _yy =υε .

В этом случае уравнение движения без учета массовых внешних сил приобретает вид [1]

Рис. 1

Учитывая зависимость σ = σ ( ε ) при нагружении и вводя обозначение

a ²( σ ) =^∂σ ,                   (5)

∂ε

где d σ / d ε – тангенс угла наклона касательной

∂v ∂σ ρ= .

∂ t ∂ x

Поскольку плотность постоянна, то без потери общности ниже полагаем ρ= 1 .

Принимая определяющие соотношения деформационной теории пластичности (для одноосного напряженного состояния) в следующем виде

σ=σ ( ε ),

будем считать, что σ ( ε ) есть монотонно возрастающая по ε функция (рис. 1) и что для всех ε производная d σ / d ε есть монотонно убывающая функция (т. е. d ² σ / d ² ε< 0). Для напряжений σ≤σ _s ( σ _s – предел текучести) зависимость σ ( ε ), согласно закону Гука, линейна:

σ= E ε при σ≤σ _s , (3)

где Е – модуль упругости.

Из уравнений сплошности в случае малых деформаций получим соотношение

d ε dv dt dx ^.

к кривой σ ( ε ), имеем

d ε d ε ∂σ 1 ∂σ dt d σ ∂ ta ² ( σ ) ∂ t .

Подставляя соотношение (4) в (6), получим систему двух уравнений с частными производными первого порядка [1]:

dv d σ ∂ v 1 ∂σ dt dx ∂ x a ² ( σ ) ∂ t

для двух функций v ( x , t ), σ ( x , t ).

В этом уравнении a ( σ ) есть скорость распространения продольных волн в стержне.

Так как скорость распространения волн в общем случае есть функция напряжения, то система уравнений (7) является системой квазилинейных уравнений с частными производными первого порядка гиперболического типа. Определим для нее характеристики и соотношения на характеристиках.

Характеристики системы уравнений (7) определятся путем интегрирования дифференциальных уравнений характеристик:

dx = ∓ a ( σ ) dt .                       (8)

Эти уравнения в общем случае не удается проинтегрировать в плоскости ( x , t ) до того, как решена задача, так как а есть функция напряжения g ( x , t ) .

Вдоль характеристик dx = + a (g)dt выполняются соотношения dv + —-—d g = 0.              (9)

a ( g )

Эти соотношения носят название дифференциальных уравнений характеристик в плоскости годографа ( g , и ). После интегрирования получим

σ dσ v = +     — + C12 при dx = + a(g)dt.     (10)

0 a ^{( G} i )      ^,

Рассмотрим теперь простейший случай распространения волн нагружения в однородном полубеско-нечном стержне, находившемся в начальный момент в невозмущенном состоянии.

Определим решение уравнения (7) при заданных начальных условиях (условиях Коши)

v = ( x ,0) = 0                  (11)

и краевом условии

g (0, t ) = - p ( t ) ( p ( t ) >  0),            (12)

причем чтобы обеспечить процесс нагрузки, должно быть p' ( t ) >0.

Условия (11), (12) означают, что в начальный момент стержень находится в недеформированном состоянии и состоянии покоя. Удовлетворение начальным условиям связано с решением задачи Коши в области (рис. 2), ограниченной осью х и положительной характеристикой t s Q.

• 2.    Для простоты рассмотрим следующее выражение для функции (2):

G = E S при Gs,             (13)

G ( s ) = 2 Vs , при G>G s .

Общий случай рассматривается аналогично.

Для непрерывности функции g ( s ) в точке s _s полагаем E = 1/ -JSs .

В этом случае плоскость xot разобьется на две области: упругую, ограниченную осью х и прямой t s Q , и пластической областью, расположенной выше прямой t s Q . Заметим, что уравнение этой прямой имеет вид x = a ₀( t - t s ) (см. рис. 2). В упругой области имеем линейную задачу, которая без труда решается традиционными методами. Поэтому будем искать решение задачи Коши для уравнений (7) только в пластической области.

Постановка задачи. Найти значение функций v ( x , t ), g ( x , t ) в точке M ( x m , t m ), если известно значение искомых функций вдоль t s Q и t s P . Здесь точки

P (0, t_p ), Q ( x_q , t_q ) определяются как точки пересечения соответствующих характеристик, проведенных из точки М . В силу (13) уравнения (7-10) запишутся так:

dv d σ ∂σ ∂ v dt dt ∂ t ∂ x

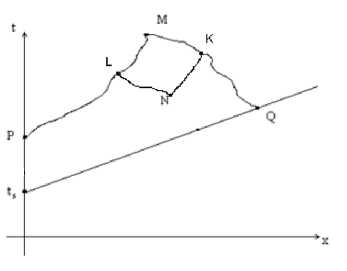
Рис. 2

Характеристики:

dx = + Vg dt .

Соотношения на характеристиках dσ dv = +-/= σ после интегрирования запишутся в виде v ± 2 Vg = C1 2.

Введем инварианты Римана по формулам £ = v + 2 Vg , П = v - 2 Vg , тогда система (7) запишется в виде

§ t =Vg^ x , n t =^-VGn x .           ⁽¹⁴⁾

• 3.    Закон сохранения ищем в виде [2] d t A & n ) + д x B & n ) =

= ⁽ Vg a ^ + B ^ ) § x + ^(-Vg A n + B n ) n x = °.

Уравнения для определения А и В :

(VGA,+ B,) = 0,(-VGAn + Bn) = 0(15)

или

2(^-n) An) - A,+ An = 0.(16)

Заметим, что для функции В мы получаем аналогичное уравнение

2(^-n) B,n) - B,+ Bn= 0.(16*)

С учетом закона сохранения запишем интеграл по замкнутому контуру t s QMP :

f Adx-Bdt =J+J+J+J= 0.(17)

tsQMP               tsQ QM MP Pts

Вдоль контуров t_sQ и Pt_s интегралы можно вычислить после определения А , В и с учетом начальных и граничных условий. Определим A , B таким образом, чтобы вдоль QM и MP интегралы были равны нулю.

Имеем

∫ Adx - Bdt = ∫ ( -σ A - B ) dt = t ( -σ A - B ) I M ₊

QM           QM                            Q

+ ∫ td ( σ A + B ),

QM

∫ Adx - Bdt = ∫ ( σ A - B ) dt = t ( σ A - B )

MP           MP

M

- ∫ td ( σ A - B ).

MP

Получаем

d ( σ A + B ) I = 0, d ( σ A - B ) I = 0. ξ= const                               η= const

С учетом (15) для уравнения (18) получаем

14 A - 2 σ A _η = 0 вдоль QM при ξ = const,

• 14 A + 2 σ A _η = 0 вдоль MP при η = const .

  
  
  
  

Для преобразования условий (19) и (20) заметим следующее. Пусть вдоль линии ξ = const нам известна функция А , тогда вдоль этой линии нам известна и A _η . Поэтому решая уравнение (19), без труда получаем

A =     ¹ вдоль QM при ξ = ξ ₀ = const. (21)

• Viη-ξ0I                      0

Аналогично из (20) имеем

A =     1 вдоль QM при η = η ₀ = const. (22)

VI ξ-η0                      0

Поэтому для определения координаты t_m точки M необходимо решить задачу Гурса (21), (22) для уравнения (16).

Определим x_m из соотношения (17).

Вдоль контуров t_sQ и Pt_s интегралы можно вычислить после определения A , B и с учетом начальных и граничных условий. Определим A , B таким образом, чтобы вдоль QM и MP интегралы были равны нулю.

Имеем

∫ Adx - Bdt = ∫ ( - A - B /v σ ) dx =

QMQM

+ ∫ xd ( A + B / σ ),

QM

= x ( - A - B / σ) | Q^M

∫ Adx - Bdt = ∫ ( A - B / σ ) dx =

MPMP

= x ( A - B / σ)|- ∫ xd ( A - B / σ ). ^M MP

Получаем

d(A+B/σ) I

ξ= const

d(A-B/ σ)I

η= const

.

С учетом уравнений (15) для уравнения (18) получаем

B + 2( ξ-η ) B _η = 0 вдоль QM при ξ=ξ ₀ = const, (24)

- B + 2( ξ - η ) B _ξ = 0 вдоль MP при η=η ₀ = const. (25)

Решая уравнение (24), без труда получаем новое граничное условие

B =Viη-ξ ₀ I вдоль QM при ξ=ξ ₀ = const. (26)

Аналогично из (25) имеем

B =Viξ-η ₀ I вдоль QM при η=η ₀ = const. (27)

Поэтому для определения координаты x m точки M необходимо решить задачу Гурса (26), (27) для уравнения (16*).

Для решения этих двух задач воспользуемся функцией Римана для уравнений (16) и (16*). Из свойств функции Римана следует, что для уравнения (16) с условиями на характеристиках (21), (22) и для уравнения (16*) с условиями (26) и (27) она будет одна и та же. Функция Римана имеет следующий вид:

υ ( ξ 0 , η 0 , ξ , η ) = ( ^{ξ 0 -η 0})¹²( ^{ξ 0 -η 0} )¹² F (1 , 1;1, t ), (28) ξ ₀ -η   ξ-η ₀22

ξ-η ξ0-η

где 1 - t = (      )( ⁰⁰ ); F – гипергеометрическая

ξ0-η ξ-η0

функция первого рода.

Окончательно получаем значение функции А в точке N ( ξ ₁, η ₁):

ξ 9

A ( N ) = A ( M ) υ ( M ) +υ ( - A  + A ξ ) d ξ+

• _{ξ 1}     2( ξ - η )

η 1

+υ ( A η^∫ ₀ 2( ξ-η )

Здесь точка М имеет координаты ( ξ ₀, η ₀).

Аналогичная формула будет для В в точке N [3].