Заполнение пропусков во входных и выходных данных с помощью алгоритма непараметрической идентификации

Введение. В теории автоматического управления принципы построения системы управления разрабатывались на основе заданной модели. Со временем оказалось, что во многих случаях модель, выбранная при проектировании, значительно отличается от реального объекта, что существенно уменьшало эффективность разработанной системы. В связи с этим возникло новое направление в науке, связанное с построением модели на основании наблюдений, полученных в условиях функционирования объекта по его входным и выходным переменным. Это направление известно сегодня как идентификация систем. Теории и методам идентификации посвящено большое количество работ в отечественной и зарубежной литературе, и в этом направлении разработаны свои принципы, подходы и методы [1-6]. Эти подходы нашли широкое применение в различных областях науки и техники, в том числе в биологии, медицине, аэронавтике, экономике, промышленности.

Я. З. Цыпкин отмечает, что задача идентификации систем (определение структуры и параметров систем по наблюдениям) является одной из основных задач современной теории и техники автоматического управления. Эта задача возникает при изучении свойств и особенностей объектов с целью последующего управления ими либо при создании адаптивных систем, в которых на основе идентификации объекта вырабатываются оптимальные управляющие воздействия [5].

В книге Эйкхоффа [6] дано следующее определение: <<Задача идентификации формулируется следующим образом: по результатам наблюдений над входными и выходными переменными системы должна быть построена оптимальная в некотором смысле модель, т. е. формализованное представление этой системы».

В исходных данных часто возникают пропуски. Пробелы (пропуски) в данных возникают вследствие множества причин, таких как невозможность наблюдения, отсутствие необходимых инструментов и т. п. Самый простой метод работы с такими данными -исключение из таблицы показателя (столбец) или объекта (строки) с пробелом. При большом количестве пропусков в данных этот подход приводит к уменьшению точности модели из-за сокращения объема выборки. Важно отметить, что в описанном случае сложность решения задачи идентификации повышается, особенно когда плотность пропусков высока, их расположение нерегулярно, а данных недостаточно (крайне мало У

В данной работе реализован один из алгоритмов заполнения пропусков в данных. На сегодняшний день разработано множество методов заполнения пропусков в данных. В работах [2-7] приводятся результаты работы этих методов в различных условиях. Методы заполнения пропусков реализованы в некоторых пакетах прикладных математических программ (например, SPSS Statist!с). Задача оценки влияния применения этих методов на точность решения задачи идентификации является актуальной.

Постановка задачи. На рис. 1 представлена общая схема исследуемого процесса, принятая в теории идентификации.

Представленная схема состоит из двух блоков: «Объект», «Модель». На рис. 1 используются следующие обозначения: А - неизвестный оператор объекта; u ( t ) = ( u 1 ( 1),u ₂( i X .... u _mf )) eQ ( u ) c R^m - векторное входное воздействие объекта размерностью m ; x ( t ) = ( x q, f,xf t ,, (.,e_nf( (eQ( x ) c R^e - векторная выходная переменная объекта размерностью e ; выполняется условие т >  п ; ( t ) - непрерывное время; A t - дискретность контроля входных-выходных переменных процесса; ^ (0 - векторная случайная помеха; блоки контроля переменных И" , И подвержены воздействию случайных помех h^u ( t) и h^x ( t ); u_t и x_t - измерения переменных u ( t ) и x ( t ) в дискретные моменты времени. Выборка измерений входных-выходных переменных процесса ^y_vu_i,x_i,i = l,s ], где s - объем выборки. Измерения входных-выходных переменных объекта поступают на блок «Модель», где на основании заданного алгоритма находятся значения выхода модели x_st . Все случайные факторы, действующие в каналах измерения и на процесс, имеют нулевые математические ожидания и ограниченные дисперсии.

Рассматриваемый процесс относится к классу дискретно-непрерывных, т. е. по своей природе процесс является непрерывным, однако входные-выходные переменные процесса контролируются через дискретные моменты времени.

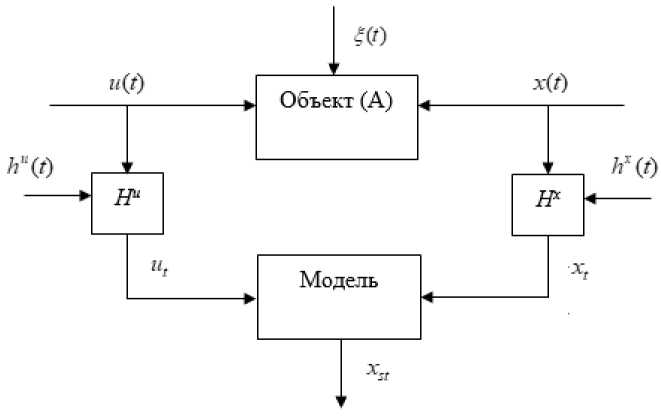
Рис.^. Общая схема исследуемого процесса

^g.^.^eneral^^eme of^he^xplored^ro^ss

При построении модели с помощью методов идентификации используются экспериментальные данные. Ведется регистрация входных и выходных сигналов системы, и модель формируется в результате обработки соответствующих данных.^

Формирование модели по наблюдениям включает:

• 1)    данные^

• 2)    множество моделей-кандидатов^

^ правило оценки степени соответствия испытываемой модели данным наблюдений.

Для построения модели важно иметь полные экспериментальные данные^ наблюдения), но на практике это встречается крайне редко, т. е. такие данные имеют пропуски. Точность решения задачи идентификации зависит от качества данных. Если удалять строки из в матрицы наблюдений, которые имеют пропуски, очевидно, что число строк будет меньше, соответственно, точность модели снизится. Поэтому существует задача заполнения таких пробелов в матрице наблюдений.^

Непараметрический алгоритм оценки кривой регрессии. Существуют параметрические и непараметрические методы идентификации. Методы параметрической идентификации требуют большого объема априорной информации. Часто возникают случаи, когда априорная информация об объекте очень бедна, поэтому структуру объекта нельзя определить с требуемой точностью. Непараметрические методы не ориентированы на указанные параметрические семейства, имеют более универсальную структуру и более широкую область применения^7^8]. В условиях малой априорной информации целесообразно использовать методы непараметрической идентификации^9; 10].^

С другой стороны, необходимо решать большое количество дополнительных задач: выбор структуры системы, задание класса моделей, оценивание степени и формы влияния входных переменных на выходные и др.^11]. Один из вариантов построения модели в условиях непараметрической неопределенности^

это применение непараметрической оценки кривой регрессии. Вид такой оценки в многомерном случае имеет вид^12^

^{х ( u} ) =

s m

2 хП ф

, = 1       j = 1

s m

2П ф

i = 1 j = 1

u^{1 -} u i

Cs .

u¹ - u i

C s

где u = ( u 1 , u 2 ,...,u 3 ) - m -мерный вектор входных воздействий объекта; х - выходная величина; Ф ( С -'( u^j — и{) ) - ядерная колоколообразная функция; C_s - коэффициент размытости ядра. Ядерная функция Ф(.) и коэффициент размытости ядра C_s удовлетворяют следующим условиям сходимости:

C s >  0 ; ^ Ф (С- 1 ( u - u i ) ) <® ;

lim C s = 0; ^ С- 1 f ф (С- 1 ( u - u i ) ) dx = 1;        (2)

s ^«

Q ( u )

lim scm = *; ^ lim С-1Ф (C-1( u1 - ui)) = 8(uj - ui), s ^«              s ^« где 5(uj -uf) - дельта-функция Дирака [13]. Ядерная функция имеет различные формы: треугольное ядро, параболическое ядро, кубическое ядро и др. Важно отметить, точность восстановления функции регрессии по наблюдениям с пропусками несущественно зависит от формы ядра и определяется практическими соображениями исследователя. В данных вычислительных экспериментах используется треугольное ядро, которое имеет вид

Г х - х Л J ^{1 -} | c - ^{1( х -} x jU с^{- 1}( ^{х - х}Л < ¹

Ф =                                   .    (

I C s J [        0, C - 1 ( х - х , ) >  1|

Для вычислительных экспериментов был выбран объект, описываемый следующей структурой:

х , = 0,5 ■ u 1 + 2 • u 2 + u 33 .                 (4)

Следует отметить, что данный вид зависимости (4) известен только в рамках данных вычислительных экспериментов. Сразу отметим, что ошибка моделирования W считается по формуле

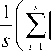
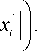
Проведенные эксперименты по заполнению пропусков в данных разделены на три этапа.

Этап I. На данном этапе имеем полностью заполненную матрицу наблюдений с входными переменными и₁, u ₂, и ₃ и выходом X i . С помощью формулы (1) находим значения оценки x i и настраиваем коэффициент размытости C_s , т. е. значение, при котором ошибка W минимальна. То есть параметр размытости C_s определяется путем решения задачи минимизации квадратичного показателя соответствия выхода объекта и выхода модели, основанного на методе <(скользящего экзамена», когда в модели 1)) исключается i -я переменная, предъявляемая для экзамена:

^{R (} c s ) = 2 ( ^xk - ^xs ( ^uk , c s ) ) ² = min, k * i .      ⁽⁶⁾

k = 1                                    c s

Важно отметить, что C_s был взят в промежутке от 0,1 до 5 с шагом 0,1.

Этап II. Добавляем пропуски по определенному правилу. Удаляем из матрицы наблюдений строчки с пробелами. Далее выполняем то же самое, что на первом этапе.

Этап III. На данном этапе восстанавливаем значения пропущенных данных в первом эксперименте по формуле (1), а во втором - по формуле

U m

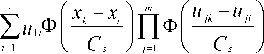
s

2 ф i =1

к *;                            к*i

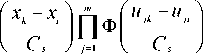
Значения пробелов заполнены, матрица наблюдений снова становится полной. Далее выполняем то же самое, что на первом этапе.

Рассмотренные этапы были реализованы на выборках S =) 3500;000;900;1000; 1000;100(1;2100.

Далее рассмотрим результаты вычислительных экспериментов.

Первый вычислительный эксперимент. В рассматриваемом эксперименте пропуски находятся в выходных данных (во всех значениях x i , кроме каждого третьего). Дискретность таких пропусков объясняется особенностью контроля выхода. Это означает, что одни переменные процесса измеряются в один промежуток времени, другие - в другой. На практике часто встречаются данные с различной дискретностью контроля выхода, например в процессах сжигания угля в котлоагрегате энергоблока, кислородноконвертерной плавки стали.

Значения входных переменных сгенерированы случайным образом в промежутке от 0 до 3 с точностью 00)0001.

Этап I. Найдены значения оценки x " при заполненной матрице наблюдений.

Этап II. Удалены строчки с пробелами из матрицы наблюдений. В результате выборка уменьшилась в 3 раза. Снова находим значения оценки x .

Этап III. Восстановлены пропущенные значения в матрице наблюдений.

Результаты данного вычислительного эксперимента представлены в табл.1.

После изучения табл. 1 следуют следующие выводы:

• 1.    При увеличении выборки S уменьшается ошибка моделирования (5). Это говорит о том, что чем больше текущая информация, тем точнее модель.

• 2.    Результаты 2 этапа во всех случаях хуже итогов 1 и 3 этапов. Очевидно, что выборка на 2 этапе меньше остальных, поэтому ошибка (5) больше ( W 1 s < W 2 s , W 3 s <  W 2 s ; Cs 1 <  C 2 s , Cs 3 <  C s 2 ).

• 3.    Результаты на 3 этапе во всех случаях лучше итогов 1 этапа ( W _{3 s} <  W _{1 s} <  W _{2 s} ). В большинстве случаев C_{s 1} = C_{s 3}, в остальных случаях - отличие в одну десятую, это говорит о правильности реализации алгоритма.

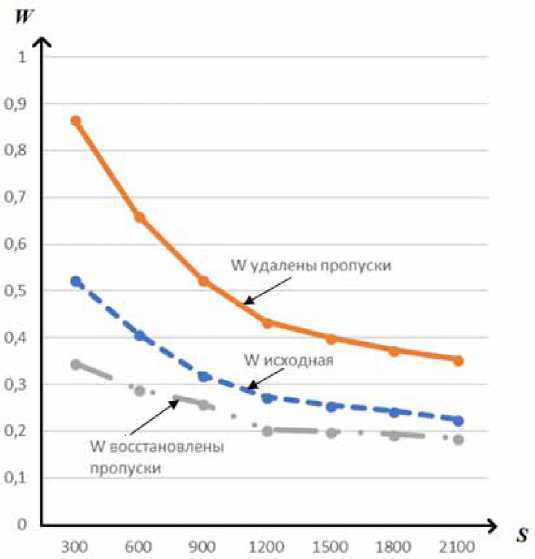
На рис. 2 представлен график зависимости ошибки W от объема выборки S .

Важно отметить, что с увеличением выборки уменьшается ошибка моделирования (5). Поэтому чем больше данных, тем точнее будет результат.

Вышеописанные выводы доказывают эффективность применения непараметрического метода для заполнения пропусков и построения модели при малой априорной информации.

Второй вычислительный эксперимент. В отличие от первого эксперимента, теперь пропуск находится во входных данных, а именно, в каждой 5-й строке в случайной переменной и , или и ₂, или и ₃.

Рассматриваемый эксперимент будет проведен с разными входными данными. В первом случае между входами есть некоторые зависимости:

и ₂ = 0,5 • и + 0,1 - g ,                       (8)

и ₃ = 0,5 • и ₁ + 0,3 • и ₂ + 0,05 • g ,                   (9)

где g -) случайным образом сгенерированное число в промежутке от 0 до 3 с точностью 00)01.

Коэффициент корреляции на всех выборках составляет примерно 0,77. Во втором случае данные сгенерированы случайным образом в промежутке от 0 доз.

Этап I. Найдены значения оценки x " при заполненной матрице наблюдений.

Этап II. Удалены строчки с пробелами из матрицы наблюдений. Тем самым выборка сокращается на 20%. Снова находим значения оценки x " .

Этап III. Восстановлены пропущенные значения в матрице наблюдений.

Результаты данного вычислительного эксперимента представлены в табл. 2.

Подведем некоторые выводы по табл.^. В данном эксперименте от общего объема выборки пропусков не так много, поэтому процедура удаления строк с пробелами не дает существенного отличия от ре- зультатов^- го этапа^ в пределах пяти сотых). Интересно следующее: по результатам^- го этапа ошибка^5) увеличивается даже в сравнении со^- м этапом.^

Таблица 1

2 Структура модели: x 1 = « 1 u 1 + a 2 u 22 + a 3 u 33
5	1 этап		этап^		этап
	W 1	Cs 1	W 2	C s 2	W 3	C s 3
300	0,5249346	0,6^,86835	486^,8           0	,34579805	0,6	0,6
600	0,40851948	0,5^,66137	73            0,6^	,2906845	0,5	0,5
900	0,32048658	0,4^,52412	224^,6           0	,25944132	0,5	0,5
1200	0,27469125	0,4^,43487	462^,5           0	,20380524	0,4	0,4
1500	0,25636882	0,4^,40102	375^,5           0	,19891156	0,4	0,4
1800	0,2437991	0,4^,37384	215^,5           0	,19284262	0,4	0,4
2100	0,22616474^,3	0,35352	94            0,5^	,18599847	0,4	0,4

Результаты вычислительного эксперимента

W исходная

300    600    900   1200   1500   1800

-----» 2100

W восстановлены пропуски

W удалены пропуски

• Рис.^. График зависимости относительной ошибки^5)^ от объема выборки на разных этапах экспериментов

^g.^.^he^raph^f^ependence of^he^elative^rror^5)^ on^he^ample^i^ at^ifferent^tages^f^he^xperiments

Результаты вычислительного эксперимента с зависимыми между собой входами с пропусками в каждой 5-й строке матрицы наблюдений

Таблица 2

2 Структура модели: x 1 = a 1 u 1 + a 2 u 2 + a 3 u 3
S	1 этап		этап^		этап
	W 1	Cs 1	W 2	C s 2	W 3	C s 3
300^,10365	894          0,2	0,10734	4694          0,2	0,17787	787           0,3	0,3
600^,09081	579           0,2	0,09373	3266          0,2	0,18755	85            0,3	0,3
900^,04582	2605          0,1	0,0487	4478          0,1	0,12278	164          0,2	0,2
1200^,0356	5259          0,1	0,04058	9087          0,1	0,12119	869          0,2	0,2

Таблица 3

Результаты вычислительного эксперимента 3-го и 4 -го этапа с пропуском во входных переменных в каждой пятой строке

2 Структура модели: х 1 = a 1 и 1 + a 2 и 2 2 + a 3 и 3 3
S	3 этап		этап
	W 1	Сs 1	W 2	C s 2
300	0,17787787^,3	1,3138921	1,3138921	0,9
600	0,1875585^,3^,218	4308                   0	,9	0,9
900^,1227816	4                    0,2	1,1859775	0,85	0,85
1200^,1211986	9                   0,2	1,073532	1                       0,8	0,8

И

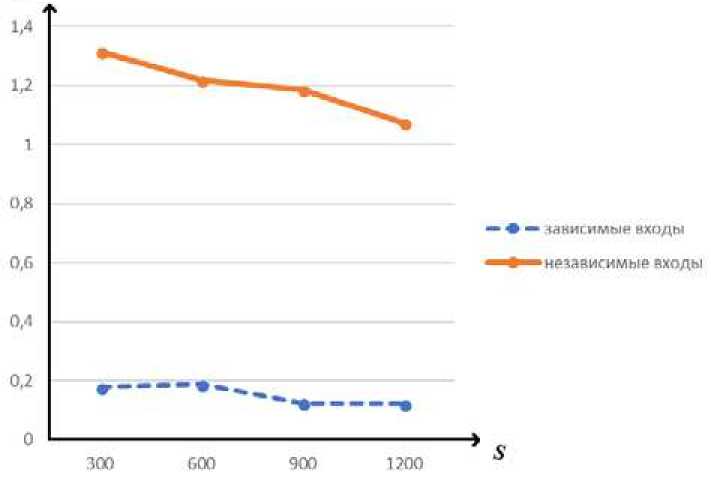
Рис.З. График зависимости W ot S в модели (4) при наличии пропуска в каждой пятой строке матрицы наблюдений на входе

Fig.3.Theeoaphoftfedependence of W on S in the m

Также был проведен этот же эксперимент, но с двумя входными переменными. Картина сохранилась, по результатам^- го этапа ошибка^5) увеличивается даже в сравнении со^- м этапом.^

Данные результаты говорят о том, что эффективность применения этого алгоритма к данным,^ содержащим пропуски по входным переменным,^ значительно ниже, чем к данным с пропусками^ по выходам.

Далее эксперимент был повторен с независимыми между собой входными данными. Пусть это будет^ 4-й этап. Результаты^- го и^- го этапа представлены^ в табл.^.^

На рис. 3 представлен график зависимости W от S в модели^4), визуализирующий данные из табл.^.

По вышеописанным данным следует вывод, что при независимых между собой входах результаты в несколько раз хуже, чем при зависимых. Это говорит о том, что использование непараметрического алго- ритма для восстановления пропусков на входах при независимых между собой значениях в матрице наблюдений нецелесообразно использовать^ или использовать, но в задачах, не требующих большой точности). Предполагается, что в строках и столбцах имеется избыточность, т. е. между свойствами могут быть зависимости, а объекты могут быть похожи между собой. Если избыточность не наблюдается, то все строки и столбцы имеют одинаковый вес при прогнозировании и смысл локальности алгоритма теряется, что и происходит при независимых данных^14].

Далее проведем исследование, аналогичное прошлому эксперименту. Но теперь будет пропуск в каждой

3-й строке в случайной переменной и 1 или и 2 , или и 3 .

Результаты проведенного исследования представлены в табл.^.

Результат на^- м этапе хуже, чем на первом и вто-ром^ почти всегда), но разрыв между результатами относительно небольшой.^

На рис.^ представлен график зависимости ошибки (5) от объема выборки текущего и прошлого эксперимента с зависимыми между собой данными в матрице наблюдений для модели^4).

В данном эксперименте по сравнению с прошлым пробелов в матрице наблюдений больше. По графикам очевидно, что ошибка^5) меньше в текущем эксперименте, т. е. получается так, что при малой апри- орной информации непараметрические алгоритмы имеют высокую эффективность.

Далее эксперимент был повторен с независимыми между собой входными данными. Пусть это будет 4-й этап. Результаты^- го и^- го этапа представлены в табл.^.^

Визуализация результатов табл.^ представлена на рис.^.

Таблица 4

Результаты вычислительного эксперимента с зависимыми между собой входами с пропусками в каждой 3-й строке матрицы наблюдений

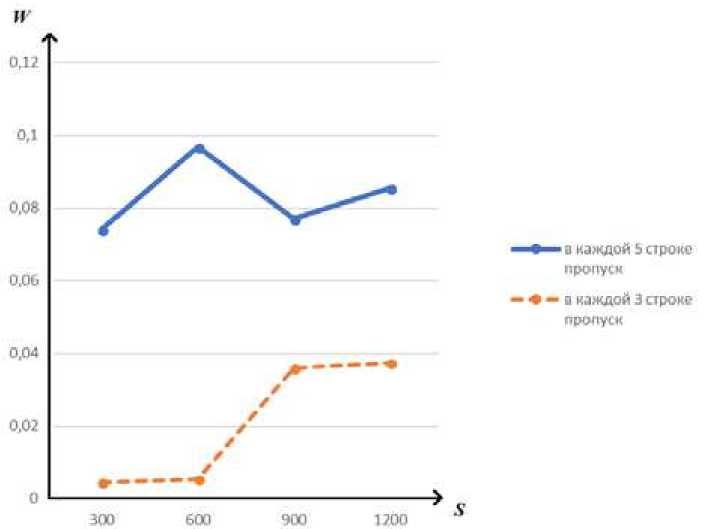
Рис.4. График зависимости W от S проведенных экспериментов в модели (4)

2 Структура модели: x 1 = a 1 u 1 + a 2 u 2 + a 3 u 33
S	1 этап		этап^		этап
	W i	Cs 1	W 2	C s 2	W 3	C s 3
300	0,10365894^,2^	,11760777	0,2           0,	10815763	0,2	0,2
600	0,09081579^,2^	,09333572	0,2           0,	09623865	0,2	0,2
900^,04582	2605          0,1	0,05677	2906          0,1	0,08182	337          0,2	0,2
1200^,0356	5259          0,1	0,04768	9456          0,1	0,07308	948          0,2	0,2

Fig.4.Thapoaphoftfxdependence of W on S ofOfexxperimenSscarriedouninmodel (4)

Результаты вычислительного эксперимента 3-го и 4 -го этапа с пропуском во входных переменных в каждой третьей строке

Таблица 5

2 Структура модели: x 1 = a 1 u 1 + a 2 u 2 + a 3 u 3 3
S	3 этап		этап
	W i	Cs 1	W 2	C s 2
300^,1081576	3                      0,2	0,6380898	0,6380898	0,9
600^,0962386	5                    0,2	0,4356285	0,4356285	0,6
900^,0818233	7                    0,2	0,3983642	0,3983642	0,6
1200^,0730894	8                   0,2	0,371171	5                       0,6	0,6

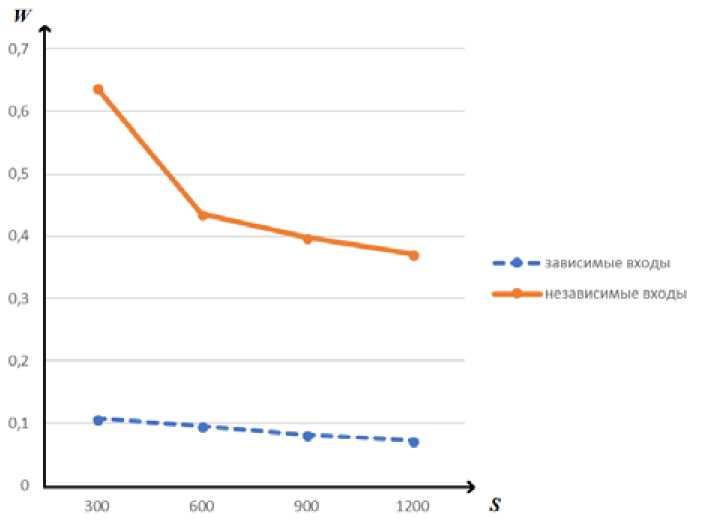
Рис.^. График зависимости ошибки^5) от объема выборки в модели^4)

^g.^.^he^raph^f^he^ependence^f^he e rror^5)^n^he^ample^i^^n^he^odel^4)

Анализируя графики и табл.^, еще раз можно убедиться в том, что при независимых между собой входах результаты в несколько раз хуже, чем при зависимых. Использование непараметрического алгоритма для восстановления пропусков при случайных входных значениях в матрице наблюдений нецелесообразно.

Заключение. Вышеописанные выводы доказывают эффективность применения непараметрического алгоритма для заполнения пропусков и построения модели при малой априорной информации. Ошибка моделирования^5) по заполненной матрице наблюдений с помощью рассматриваемого алгоритма оказалась меньше, чем по исходной.

Эффективность применения непараметрического алгоритма к данным, содержащим пропуски по входным переменным, значительно ниже, чем к данным с пропусками по выходам. Также важно отметить, что при зависимых входных данных результат работы алгоритма будет намного точнее, что описано в гипотезе избыточности^15].

В дальнейшем планируется исследование^et-алгоритма, а именно, его применение в задаче заполнения пропусков в данных. Также будет проведено сравнение результатов работы^et- алгоритма с алгоритмом непараметрической оценки кривой рег-рессии.^