Запутанность спиновых состояний четырехфермионной системы

Использование спина в качестве носителя квантовой информации в устройствах спинтроники [1-2] требует изучения свойств реальных физических спиновых систем. Несмотря на. то, что носителем информации, в принципе, может быть спин отдельного электрона, в реальных экспериментах электронный спин «генетически» связан с породившим его ансамблем. В работах [3-4] показано, что принцип неразличимости электронов и принцип Паули (требование антисимметрии полной волновой функции) однозначно определяют спиновое состояние мезоскопической системы нескольких фермионов со спином S = 1/2, например электронов, находящихся в одной области пространства. Это состояние должно описываться спиновой матрицей плотности, которая не зависит от вида, пространственных частей одночастичных волновых функций. Спиновая матрица плотности позволяет изучать физические корреляции спинов фермионов, однако потенциальные применения таких спиновых ансамблей требуют изучения их «информационных» свойств. Среди таких свойств важную роль играет запутанность квантовых состояний.

Информационная значимость запутанности квантовых состояний [5-6] известна, и хорошо описана, в литературе. Гораздо меньше внимания уделялось проблеме происхождения запутанности в реальных спиновых системах. Большинство работ, посвященных изучению разных случаев запутанности, не ставили проблему ее происхождения. Основной причиной происхождения запутанности считались взаимодействия между частицами, (например, кулоновское или обменное взаимодействие [7-8]). Строго говоря, обменные взаимодействия проявляются лишь в случае сильного перекрывания волновых функций фермионов, а. «реализация» обменного взаимодействия является следствием принципа Паули, требующего антисимметрии полной волновой функции фермионов Ф. Теоретические исследования запутанности спиновых систем зачастую ограничивались простыми двухспиновыми моделями.

Цель данной работы: определить спиновые состояния невзаимодействующих фермионов, находящихся в одной области пространства, и подчиняющихся принципу Паули; описать и изучить их спиновые корреляции; исследовать спиновую запутанность как в 4-фермионной системе, так и в ее подсистемах.

2.    Построение четырехспиновой матрицы плотности

Описание свойств мезоскопической спиновой системы удобно начатв с анализа, спиновых состояний и свойств четырехэлектронной системы. Её физической реализацией может быть, например, атом бериллия Be с четырьмя электронами на. 1s- и 2з-орбиталях, четыре электрона на двух л-орбиталях молекулы этилена и другие молекулы с заполненными электронными оболочками. Четырехспиновая система, во-первых, качественно отличается от хорошо изученной двухспиновой системы, а во-вторых, позволяет определить основные свойства многоспиновых фермионых систем и наметить основные подходы к их исследованию.

Стартовой позицией для описания таких систем является полная волновая функция |Ф ( г, 8^)), антисимметричная относительно перестановок любых частиц (принцип Паули). Совокупность электронных спинов неразличимых частиц (фермионов) образуют спиновую подсистему, состояние которой в силу принципа, несепарабельности [9] должно описываться спиновой матрицей плотности. Согласно общим правилам такие редуцированные матрицы плотности подсистем находятся взятием частичного следа, по «лишним переменным» полной матрицы плотности

Р⁵ = Tr_ip^l^⁽r_j ,8 3 ^))ф (г j ,8 3 )|. (1)

В работах [10-11] показано, что после вычисления антисимметричной волновой функции |Ф(г^,8г)) и взятия следа по совокупностям пространственных волновых функций Рг(г) спиновая матрица плотности может быть представлена в виде р5 = 3 {|S12S34)(S12S34| + | S13S24)(S13S241 + |S14S23HS14S23|} .

Здесь оператор матрицы плотности р⁵ представлен в виде суммы трех операторов проектирования на парные синглетные спиновые состояния \S tj 8 ы ). Полученное выражение (2) и представляет собой искомую спиновую матрицу плотности четырехэлектронной (четырехфермионной) системы. Оно не зависит от конкретного вида, пространственных одноэлектронных волновых функций ppr). Вывод матрицы плотности (2) без дополнительных предположений из антисимметричной волновой функции |Ф (г^, 8^)) доказывает, что спиновая матрица плотности р⁵ однозначно определяется принципом неразличимости квантовых частиц и принципом Паули.

Вид оператора матрицы плотности р⁵ делает очевидной ее симметрию относительно любых перестановок. Перестановки спинов внутри одного синглета, изменяют знак вектора, спинового состояния IS ij ) = 2-2 Ia t 3 j — З г « з) ^{но не} изменяют знак тензорного произведения этих векторов. Перестановки спинов между разными синглетами сводятся к простой перестановке операторов проектирования. Таким образом, показано, что из антисимметричной волновой функции Ф получена симметричная матрица плотности р⁵. Поскольку все парные синглетные состояния инвариантны относительно вращений, то и матрица, плотности р⁵ инвариантна относительно этих преобразований.

Оператор матрицы плотности (2) представлен в обычной форме суммы операторов проектирования на парные синглетные состояния IS^jS^i) Однако скалярные произведения этих векторов спиновых состояний:

(^S 12 ^S 34 ^{1 S} 13 ^S 24 ) = 2 ,   (^S 12 ^S 34 | ^S 14 ^S 23 ) =

-

2 ,   (^S 13 ^S 24 ^{1 S} 14 ^S 23 ) = 2.

Таким образом, операторы проектирования Р = IS 13 S 24X S 13 S 24 I не являются ортогональными проекторами, следовательно, мы имеем представление оператора, матрицы плотности (2) в виде суммы 3-х неортогональных операторов

Р 1 = |S 12 S 34 )(S 12 S 34 |,  Р 2 = IS 13 S 24X S 13 S 24 I,   Р з = IS 14 S 23X S 14 S 23 I.

Легко показать, что неортогональные спиновые векторы ISijSp) линейно зависимы и любой из них может быть представлен как суперпозиция двух других. Это означает, что они принадлежат двумерному подпространству полного пространства спиновых векторов четырехспиновой системы (размерность полного пространства 24 = 16) и могут быть представлены как обычные векторы на плоскости. Введение обозначений

|1> = 1512534),   |2> = 1513^24),   |3> = 1514^23);   |4> = 3-1/2 (|S13S24> + IS14S23» , позволяет наглядно представить взаиморасположение этих векторов, представленное на. (рис. 1).

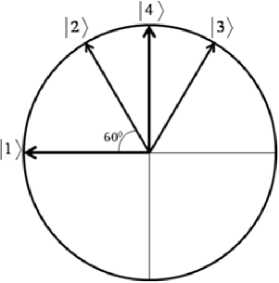
Рис. 1. Векторная модель спиновых состояний четырехэлектронной системы

Прямые вычисления показывают, что спиновый вектор |4> нормирован и ортогонален вектору |1> = | 5125з4 >. Выразив все спиновые векторы \S i3 5 ы >  через векторы |1> и |4>, можно получить выражение для матрицы плотности p^s в ортогональном базисе:

P^S = 2(|1>(1| + |4>(4|).                                           13)

Из (3) следует, что p^s пропорциональна единичной матрице I, размерность которой равна 2. Вектор |4> удобно представить в виде

|4> = 3-1/2|т+2734 + Т-2Т+ - ТМ), где |Т±,о> — векторы триплетных состояний электронных спинов

| Т + } = |CY_ІCY₃ >,   Т ) =2^-1/2к Р₃ + Р г «₃ >, |т- } = М >.

Матрица, плотности (3) описывает простую некогерентную суперпозицию двух четырехспиновых состояний, полный спин которых 5 = 0.

Умножение выражения (3) на 2 дает в левой части двумерный единичный оператор I, который одновременно является и оператором проектирования на. двумерное подпространство четырехспиновых синглетных состояний В о- Поскольку выражения (2) и (3) описывают один и тот же оператор, то и оператор проектирования В о, допускает представление в виде суммы неортогональных проекторов

Р о = 3 {|5 12 5 34 >(5 12 5 34 | + |5 13 5 24 >(5 13 5 24 | + 15 14 5 23X 5 14 5 23 1} .             (4)

Это выражение очень полезно при анализе спиновых эффектов в многоспиновых системах, поскольку позволяет легко описать многоспиновые правила, отбора, которые неизбежно действуют во многих физико-химических процессах и реакциях. Такое представление оператора проектирования легко обобщается на более сложные случаи синглетных состояний многоспиновых систем.

3.    Спиновые состояния подсистем четырехфермионной системы

Полученное выражение для четырехспиновой матрицы плотности p^S системы электронов с заполненными электронными оболочками позволяет изучать спиновые состояния частиц внутри ансамбля и получать выражения для спиновых матриц, описывающие электронные системы с незаполненными оболочками. Физически такие системы можно получить, исключив «лишний» спин, принадлежащий удаляемому электрону.

Удалению «лишнего» спина, соответствует редукция спиновой матрицы плотности по переменным удаляемой частицы. Поскольку изначально все частицы эквивалентны, то «удалять» можно любую из них, это не изменит конечный результат. Здесь для простоты и удобства, будем считать, что удаляется четвертый спин. Поэтому и редукцию спиновой матрицы плотности проведем по его спиновым переменным.

Редуцированная матрица, плотности

Р 123 = TT'4_;p^S = (a 4 |p^S |« 4 ) + (/3 4 |p⁵ Д4 ).                            (5)

В результате получаем

Р 123 = б(^|5 12 )(5 12 |(^|а з )(а з | + І^ зХ ^ з |) + ^|S i3X ^S i3 ^|(|a 2H ^a 2 | + |А M^D + ⁺ |5 2зМ 5 2зШ^а1М^а1 | ⁺ |AXAD .

Эта матрица плотности р123 представляет собой сумму произведений матриц плотности парных синглетных состояний IS -j}(Sij | на матрицу плотности неполяризованного неспаренного спина |а)(а| +ДД,в|, причем неспаренным может быть любой из спинов системы 1, 2 или 3. Таким образом, редукция спиновой матрицы плотности по спиновым переменным удаляемой частицы сохраняет неразличимость оставшихся частиц.

Матрицу плотности 2-х спиновой подсистемы можно получить либо сразу из спиновой матрицы pS редукцией по спиновым переменным «лишних» фермионов, например, по переменным 3 и 4 частиц, либо из матрицы pi23 редукцией по переменным третьей частицы.

p i2 = ^T 3 p i23 = TT 34 p^S. (7)

Очевидно, что оба. способа, должны привести к одному и тому же результату. Двухспиновая матрица pi2 плотности имеет вид pi2 = 2|S12XS12I + 6 (|т+2><Т+2| + |т02><т02| + уг^т-У), (8) где |Т1±2’0^ — векторы триплетных состояний оставшихся первого и второго электронных спинов.

Из (8) следует, что спиновое состояние любой электронной пары в четырехэлектронной диамагнитной системе является некогерентной суперпозицией синглетных и триплетных состояний. Это означает, что принцип Паули не допускает существования внутри ансамбля фермионов пар частиц в чистом синглетном состоянии. Их состояния всегда являются смесью синглетных и триплетных состояний.

4.    Запутанность спиновых систем

В настоящее время известны несколько критериев запутанности квантовых состояний [12-13]. Некоторые из них, например, критерий [14], применимы лишь для двухспиновых состояний, чистых или смешанных. Для исследований запутанности квантовых спиновых систем наиболее удобным представляется критерий Переса-Городецкого [15], пригодный для сложных систем, находящихся в смешанном состоянии и описываемых матрицей плотности p p = ^р^ ^Д^.                        (9)

ijkl

Этот критерий предполагает расчет собственных значений матрицы р^Т, получаемой из исходной матрицы р транспонированием состояний одной из подсистем изучаемой квантовой системы. Доказано [16], что если в системе нет запутанности подсистем и она. может быть описана, матрицей плотности типа.

р =(I ад i) = Е₽Й (і w ң» I (i1) =       (i о» I ® I k)(i|),          no)

ijkl                     ijkl                          ijkl то транспонирование состояний второй подсистемы оставляет все собственные значения АТ матрицы рт положительными. Частичное транспонирование означает перестановку состояний одной из подсистем, то есть замены |k) ^ |l), (l| ^ (k| , переводящие оператор матрицы плотности р в оператор

Р^Т = ^ Ри ШзЦ- Ui) ijkl

Если же исходная квантовая система несепарабельна, то среди собственных значений матрицы рТ, появляются отрицательные величины АТ < 0. Этот критерий является достаточным: если есть отрицательные собственные значения, то подсистемы запутаны. Однако положительность всех собственных значений АТ > 0 матрицы рТ не гарантирует отсутствия запутанности [17].

Появление отрицательных собственных значений у матрицы р^Т не позволяет считать ее матрицей плотности. По своему определению [18] матрица плотности р должна быть положительно определенной матрицей и никакая физически возможная манипуляция, описываемая унитарными операторами эволюции, не способна вывести ее из класса положительно определенных матриц. Это означает, что в самом общем случае математической операции частичного транспонирования состояний запутанной системы не может соответствовать даже гипотетический физический эксперимент. Следовательно, необходим поиск критериев запутанности, допускающих экспериментальные реализации, но, по крайней мере, не допускающих выхода матриц плотности р из класса положительно определенных матриц.

Для изучения запутанности спиновых состояний четырехфермионной системы её матрицу плотности р (формулы (2) и (3)) удобно представить в следующем виде:

S   1 | с с \ / с* с II 1 1т+ т-     - m+   m0 т0 \/ т+ гр—     — гр+   лрО гр0 |   р = 2 Р12^34/(^12^34| + 3 |^ 12^34 + 112134 - 112134/V 12134 + 112134 - J 12^34 | =

= 2 1^ 12 ^ 34X ^ 12 ^ 34 1 + 3(|Т 1+ Т 3-4 \/Т1+Т 3-4 | + ЦЙ^Х^— 7 34 |

- |1 1+2 І 34 \/1 1 ⁰ 2 І 3 ⁰ 4 І +

- + ⟩︀⟨︀ + -        - + ⟩︀⟨︀ - +         - + ⟩︀⟨︀ 0 0

|Т 1 ^О 2 Т 3 ^О 4\№34 |-

⁺ | ¹ 12 ¹ 34/ X¹ 12 ¹ 34 1 ⁺ |¹ 12 ¹ 34/\ ¹ 12 ¹ 34 |    | ¹12¹ 34/ V 12¹ 34 |

0 0 ⟩︀⟨︀ - +         0 0 ⟩︀ ⟨︀ 0 0

|¹ 12 ¹ 34 / \ ¹ 12 ¹ 34 1 ⁺ |¹ 12 ¹ 34/ \¹12 ¹ 34 | •

Определим, существует ли запутанность между двухспиновыми подсистемами. Поскольку все частицы неразличимы, то для определенности будем рассматривать подсистемы, состоящие из частиц (1, 2) и (3, 4), и произведем перестановки состояний второй подсистемы. В этом случае перестановки |k) ^ |l) , (l| ^ (k| имеют вид

|1 4 \ ^ |Т 3°4 >,   /1 34 | ^ /1 34 |,    |14 \ ^ |1 34 \,   <1 4 | ^ <1 4 1,   ИХ ^ |1t\,

<1 4 И /1 04 |,  1IX ^ 1Х,  <1 4 Н /1 04 ,  11Х ^| IX,  /1 04 Н /1— 4 1,

1Х ^|1Х,  /14 ^ /14 |.

Перестановка синглетных состояний |1) = 15'126'34) не изменяет вида соответствующего диагонального элемента. Но после этих перестановок матрица рТ приобретает вид рТ = 2 |512^34)(512 ^34| + 3(| 1+2І4\/1+2І4| + ^Т^/Т^Т— - | ^^Х^!- |

-І-ІТТ \/ т⁺т^{+      —} Т⁺ \/ Т- Т⁺I — 1т^— Т⁰ \/Т0Т+І — ІТ⁰ Т- \/т⁺т⁰ I U-l)

⁺1¹ 12 ¹ 34/\ ¹ 12 ¹ 34 | ⁺ |¹ 12 ¹ 34/\ ¹ 12 ¹ 34 |    |¹ 12 ¹ 34/\ ¹ 12 ¹ 34 |     Ң12 ¹ 34/\ ¹ 12 ¹ 34

0 +⟩︀⟨︀ - 0          0 0 ⟩︀⟨︀ 0 0

¹ 12 ¹ 34/\ ¹ 12 ¹ 34 | ⁺ |¹ 12 ¹ 34/\ ¹ 12 ¹ 34 |).

Расчет собственных значений Аг матрицы (13) дает еле дующий набор чисел (1/2, 1/6, 1/6, 1/6, 1/6, 1/6, 1/6, -1/6, -1/6, -1/6). Три собственных значения отрицательны. Следовательно, согласно критерию Переса-Городецкого, в четырехфермионной диамагнитной системе, описываемой матрицей плотности (2), существует запутанность между двухспиновыми подсистемами. В качестве меры запутанности в данном случае удобно взять меру, предложенную в работе [19]

Е = -2 ^(А») = -2(-1/6 - 1/6 - 1/6) = 1,                   (14)

i где сумма берется по всем отрицательным собственным значениям Аг < 0 матрицы рт. Этот результат означает, что между двухспиновыми подсистемами существует максимальная запутанность, такая же, которая существует между двумя спинами, находящимися в суммарном синглетном состоянии.

В работе [20] описан другой подход к доказательству запутанности квантовых систем, основанный на применении критерия Сильвестра положительной определенности матриц [21]. Согласно этому критерию, для того чтобы матрица А = {a ij } была положительно определенной, то есть чтобы все собственные значения были положительными Аг > 0, необходимо и достаточно, чтобы все ее миноры были положительными. В простейшем случае главных миноров второго порядка, это требование сводится к простому соотношению диагональных и недиагональных элементов |aijауг | <  (ацац ). Применение этого неравенства к элементам частично транспонированной матрицы приводит к неравенству [22]

Pl j P ji < P ti P jj •                                        (15)

Если неравенство (15) нарушается хотя бы для одного набора диагональных и недиагональных элементов, то матрица р^т не является положительно определенной и имеет хотя бы одно отрицательное собственное значение.

Перестановки (13) второй подсистемы меняют суммарный спиновой момент состояний четырехфермионной системы; при этом недиагональные матричные элементы, например, р [(Т+73-4) , (T^T^)] = p_ij (S_z = 0,S_Z = 0), соответствующие состояниям с проекцией спина S_z = 0, переходят в недиагональные матричные элементы р [(T+ T+J , (Т^-2T3-4)] = p kt (S_z = +2,S_z = -2). Но в исходной матрице плотности (12) отсутствуют (равны нулю) диагональные элементы рц (S_z = +2,S_z =+2,) = 0 и P kk (S_z = - 2,S_Z = -2) = 0, которые соответствуют состояниям с суммарным спином Sz = 2. Следовательно, соответствующие миноры отрицательны и для матрицы р^тнарушается условие положительной определенности (15), она не является положительно определенной и имеет отрицательные собственные значения. Это доказывает запутанность спиновых состояний системы четырех фермионов, находящихся в одной области пространства и подчиняющихся принципу Паули. Отметим, что для реализации этой запутанности нет необходимости в физическом взаимодействии между фермионами; она. является однозначным следствием антисимметрии исходной волновой функции.

5.    Трехфермионная подсистема

Матрица, плотности 3-спиновой подсистемы получается редукцией исходной матрицы плотности (2) по переменным 4-го фермиона.

р = Тт4р = 6^(|S12M^S12| ⁰ Д ^{+ |S}13)(^S13| ^{0 I}2 ^{+ |S}23)(^S23| 0 ^I1),          (16)

где I k = |а)(а| +ДМ^|- Вид матрицы плотности (17) доказывает неразличимость спинов 1, 2 и 3. Для изучения спиновой запутанности трехспиновую матрицу плотности (17) удобно представить в полном базисе ортогональных состояний

№13), |W, IT02Q3), |Т+^3>, |Т12«з), |ТБ^з>, |S12«3), |S12^3),

Р 123 = 6(2|5 і2 а з )(5 і2 а з | + |І^К^ з І + ^зИЖД - -|^Ш^з \-

-— \1 102 _а з^ т +2 3 з \ + |\Д⁰ 2 а з ><Т 1 ⁰ 2 а з \ + | \Т2₂ЗзЖЗз\ - — \Т 02 3 з ХТ^) -   (17)

—\Т- 2 а з )(Т 02 3 з \ + ЖзЖ « з \

Частичное транспонирование, то есть перестановка состояний третьей частицы, приво-лит к матрице рХ рХз = 6(| 1^12азХ512«з| + | №23з)(^ 23з| + \Т^(Т+23з\--Д\Т+ <^123з\ - Д\Т023з><Т+щз \ + |\Т^    ТДз\ +

+|\Т 02 3 зХ Т₁ 2 3 з \ - -||Т 02 а зХ Т₁ 2 3 з |) -

-Т^ \ Т^ХТ^з \ + \ Т^з ХТ^з \.

Для этой матрицы очевидно наличие ненулевых недиагональных элементов рХ которым соответствуют нулевые диагональные элементыр^, что явно нарушает условие ее положительной определенности. Прямой расчет собственных значений А дает следующий набор (1/4, 1/4, 1/6, 1/6, 1/6, 1/6, -1/12, -1/12); здесь из восьми возможных собственных зна чений два отрицательны, что дает запутанность:

Е = -|^(Аг) = -2(-1/12 - 1/1|) = 1/3. г

Все это доказывает запутанность трехспиновой подсистемы исходной четырехфермионной системы.

6.    Свойства двухфермионной подсистемы

Матрица плотности двухспиновой подсистемы может быть получена из спиновых матриц плотности (2) или (7) редукцией по одному или двум «лишним» фермионным спинам

Р 12 = Тт з р і2з = Тт з4 р⁸ .                               (20)

Явный вид этой матрицы плотности

• р і2 = | 1'8' 12 )(5 12 | + 6 (| Т +2Х Т +2 \ + \ Т 02Х Т 02 \ + \ ТГ 2Х ТГ 2 \) .              (21)

Вид этой матрицы плотности доказывает, что в системе фермионов, подчиняющихся принципу Паули, не может быть выделена пара частиц, находящихся в чистом синглетном состоянии, описываемом матрицей плотности р = |5)(5|.

Применение критерия Переса-Городецкого показывает, что эта двухфермионная подсистема не запутана. Более того, в работе [23] дано представление этой матрицы плотности в виде суммы прямых произведений матриц плотности односпиновых подсистем. Это разложение удобно представить не в матричном, а в операторном виде рі2 = 1 {(ЬЖ 11) 0 (|32)(32|) + (|31 М311) 0 (ЫЫ) +

⁺ 4^[(|а 1 ⁺ А М^а 1 ⁺ А |) ^{0 (|а} 2 ^{- 3} 2М ^а 2 ^{- 3} 2 |) ⁺

^{+ (|}« 1 ^- А )(« 1 ^{- 3}1 |) ^{0 (|}« 2 ^{+ 3} 2 )(« 2 ^{+ 3} 2 |) ⁺

+ (|« 1 - »31 Х« 1 + «311) 0 (|« 2 + «3 2 )(« 2 - «3 2 І) +

+ (|« 1 + «3 1 М« 1 - «3 1 |) 0 (|« 2 - «3 2 )(« 2 + «3 2 І)]}.

Такое представление показывает, что квантовая система, описываемая матрицей плотности (21), может быть получена, как смесь независимых пар фермионов с антипараллель-ными ориентациями спинов вдоль осей ОХ, ОҮ и OZ.

7.    Заключение

Доказано, что принцип неразличимости частиц и принцип Паули однозначно определяет спиновые состояния фермионов, их спиновые корреляции и запутанность их спиновых состояний. Состояния спиновой подсистемы фермионов однозначно описываются спиновой матрицей плотности, которая представима, в виде суммы неортогональных проекторов на. всевозможные многоспиновые синглетные состояния.

Доказано, что в многочастичных запутанных системах могут быть незапутанные подсистемы: 4-спиновая система максимально запутана, 3-спиновая подсистема частично запутана, двухфермионная спиновая подсистема, не запутана. Показано, что двухчастичная подсистема, многофермионной системы не может быть в чистом синглетном состоянии. Доказано, что матрица плотности р описывает запутанные состояния, если для частично транспонированной матрицы рТ нарушается условие положительной определенности матрицы р^р^> р^р^.