Зародышеобразование пузырьков на дисперсных твердых частицах

Известно, что для реального жидкого металла характерно присутствие специфических примесей в виде дисперсных частиц: оксидов, нитридов, сульфидов, а также пленок окислов. Обзор литературы по этой тематике приведен в работах [1-4]. Ковалентные нитриды алюминия, галлия и индия химически устойчивы, тугоплавки, термостойки. Оксиды практически нерастворимы в алюминии, Долговременность существования мелкодисперсных включений в жидком металле определяется прочностью, и термической устойчивостью их материала. Величины прочности и термической устойчивости некоторых тугоплавких окислов, известные из работ Кинжери и других исследователей [5,6] приведены в работе [7]. Так прочность оксида Л 2 0 3 -15,4 кг/см², при температуре Т_тах = 1900^оС , оксида Si0 2 -16,8 кг/см² при Т_тах = 1100С . Термическая устойчивость при оценке на качественном уровне: хорошая и отличная соответственно.

В таблице 1 приведены значения углов смачивания некоторых оксидов и веществ в расплавах олова и висмута [5-9], Таблица 1

Sn	Л/20 з	S1 2 H 2	Графит	Мо
9 °	174	166	156	130
Bi 9 °	150	140	136	160

Для оксидных частиц в алюминии при температуре до 800 °C значения угла смачивания 0 = 150 ° — 160 ° [1].

При кавитации и кипении чистой жидкости обычно рассматривается гетерогенное образование зародыша пузырька и его рост до критического радиуса на дефектах твердой поверхности [10-11]. В ряде работ было показано снижение работы образования - W_ks для критического зародыша на дефектах конической формы, цилиндрической формы и других дефектах твердой протяженной поверхности [10]. Обширный обзор этих работ приведен в монографии [10]. Банковым было получено выражение для работы зародышеобразования на выступе твердой поверхности, согласно которому она выше по сравнению с величиной на плоской поверхности [11]:

W_ks = W_k ф(а, в) , где Ф(а, в) - функция углов а и (.   (1)

На основании анализа выражения (1) для работы образования критического зародыша для выступа был сделан вывод, что сферический выступ на твердой поверхности не может рассматриваться как потенциальный центр зародышеобразования [11]. Для случая плоской твердой поверхности указанная функция (1) практически совпадает с функцией Фольмера, зависящей только от угла смачивания ф(6) [10-12] . Детальный физический анализ для случая чисто парового пузырька с использованием функции Ф(9) дан в монографии [13].

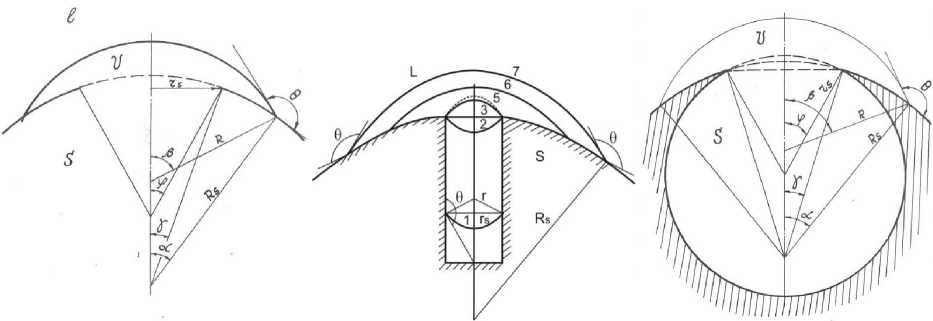
В расплавах металлов, не содержащих растворенного газа, гетерогенное зародышеобразование паровой фазы может реализоваться на мелкодис- персных частицах различной природы, возможные модели которых приведены на рис. 1a,b,c.

a

b

c

Рис.1abc Модели мелкодисперсных примесей в расплавах металлов: a – c конической впадиной, b – цилиндрической впадиной, c – резервуарной впадиной.

Выражения для работы зародышеобразования для этих моделей приведены ниже (2). Для случая отсутствия дефектов поверхности сферической частицы и асимметричного роста пузырька значение работы образования должно незначительно отличаться от работы на выступе сферической формы. Поэтому по сравнению с выражением для работы образования на выступе или впадине (1) выражение для этих моделей (2 ) включает в себя функции Банкова [11] и усложняется в зависимости от формы впадины:

< = 1^(а,в,у,ф)   (2), где

Ф5 (а, в, у, ф) = 3 sin2 в [f (а, р) - cos 0

sin2Y sin2 а

fA(Y,P)\

— If (ар) I

sin2v

Y—^^f v ⁽Y^,P^)] , где ! д ^(а,в) и f v ^(a,e) функции Банкова [11].

Для случая конической впадины на сферической частице (рис.1а) в выражении (2):

to. ф) = (1+1S7 - 2^) , My,ф) = (tg2 2 + 3tgY + 2ctgv).

b

a

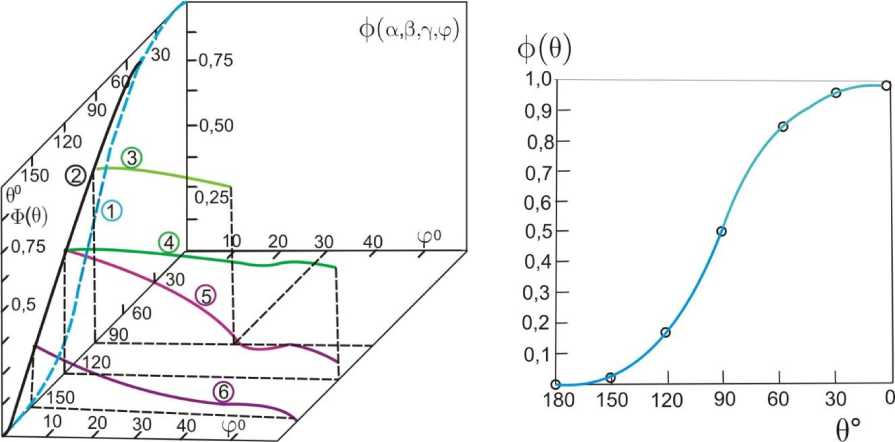
Рис 2ab. a) функция , для случая сферической частицы с конической впадиной в зависимости от угла фи 6 при значении угла в = 120⁰. r_s/R_s = 1/2.

• 1    – функции Банкова для выступа. 2 – функция Фольмера 3 6 = 90⁰, а = 30⁰, sin у = 1/2 sinф . 4. 6 = 120 0 . а = 60⁰ , sin у = 1/2 sinф . 5 6 = 120⁰ , а = 60⁰ , у = ф. 6 6 = 150⁰, а = 90⁰ , у = ф .

• b) Зависимость функции Фольмера от угла смачивания для случая плоской поверхности,

  На риc.2a и 2b для сравнения приведены также значения функции Фоль-мера - Ф(6). Выражение 0 = 180⁰-(^-а), полученное Банковым для

выступа используется, но соотношение между радиусом критического пузырька

и радиусом выступа: R_s = R *

sin а sin ^

не может быть непосред-

ственно использовано в данном расчете из-за большего количества углов и более сложной связи между ними. Так например, при равенстве углов

Y = ф, ( sin y = sin ф) коническая впадина имеет вид центрального сек тора, при равенстве углов у = а, - узкого центрального сектора. Поэтому при расчете соотношение углов задается в функциональном виде.

Результаты расчетов Ф(а, в, у, ф) представлены на рис.2 для трех значений угла смачивания 6=90 ° - кривая 3, 120 ° - кривые 4,5, 150 ° -кривая 6. Углы а, в связаны с углом 6 соотношением: 6 = 180 ° — (в — а), в = 120 ° , угол а соответственно принимает значения: 30 ° , 60 ° и 90 ° . Полученные данные при радиусе горловины r ° = 0,5/?_s , sin у = 0,5 sinф , для указанной функции (кривая - 3), незначительно отличаются от данных для случая зарождения на выступе (кривая -2). Причем, они остаются выше, чем для плоской поверхности (кривая 1). Для впадины с центральным сектором (углы у = ф) и увеличения угла смачивания 6 > 120 ° (кривые - 5,6) значения функции Ф(а, в,у, ф) существенно снижаются и работа зародышеобразования на дисперсной частице делается меньше, чем на плоской поверхности.

Для резервуарной впадины выражение (2) примет вид:

А<У-^ = (т;^ —1-^ М^Д^+З^ + Я^ 3ctg(f))

Значение функции - Ф(а, в, У, ф) в этом случае всегда ниже, чем для конической впадины, а для углов смачивания 0 > 120 ° , расчетные значения работы зародышеобразования значения ничтожно малы по сравнению с работой в однородной жидкости. Наибольшие значения работы зародышеобразования характерны для модели с цилиндрической впадиной при тех же значениях углов смачивания. Как известно, на протяженной плоской поверхности для несмачиваемой впадины цилиндрического типа, пузырек критического радиуса может расти на участке поверхности, окружающий горловину [10]. Для случая дисперсной частицы с радиусом горловины г ° для случая R_s >> г ° предположение о росте пузырька на этом участке означает пренебрежение кривизной и допущение случайного преобладания актов переноса вакансий в область растущего пузырька [14,15].

В самой цилиндрической поре первичный пузырек может сохраняться длительное время, и такая пора является потенциальным активным центром зародышеобразования. Сложный вопрос, о возможной связи оксидов с растворенным водородом в расплавленном алюминии в зависимости от температуры и давления рассматривался в ряде работ и находится вне рамок данной работы [3-4].

Мелкодисперсные частицы для случая зарождения должны находиться в жидкости или в объеме жидкого металла во взвешенном состоянии. Динамика мелкодисперсных частиц в расплавах металлов оценивалось в работе [7]. В этой связи представляет интерес сопоставление гравитационного и броуновского смещения частицы в расплавах металлов. Влияние броуновского движения на смещение сферических частиц в расплавах легкоплавких металлов было оценено в работе [7]. С этой целью использовалось модифицированное выражение Эйнштейна – Смолуховского, приведенное в известной монографии [16,17]. Броуновское смещение значительно преобладает над гравитационным смещением для частиц с радиусом R_s < 0,5 микрона, гравитационное смещение преобладает - у частиц с радиусом R_s > 1 микрона.