Защита авторских прав на глубокие модели классификации изображений

Несмотря на обилие предобученных моделей глубокого обучения в открытом доступе, искусственный интеллект зачастую применяется для решения частных задач, возникающих в коммерческих и государственных структурах. Процесс подготовки конечного продукта включает обучение глубокой нейронной сети, а следовательно, требует материальных затрат на сбор и подготовку данных, оплату специалистов и покупку необходимого оборудования. Очевидно, полученная в результате интеллектуальная собственность может вызвать интерес у злоумышленников. Таким образом, у законных владельцев возникает необходимость защиты авторских прав на глубокие модели нейронных сетей.

Для защиты авторских прав на цифровые объекты, как правило, используются цифровые водяные знаки (ЦВЗ), которые встраиваются в защищаемые данные и впоследствии могут быть извлечены для подтверждения права собственности на объект. При этом встроенный ЦВЗ должен обеспечивать стойкость к попыткам его злоумышленного удаления без значи- тельного повреждения данных. Несмотря на распространенность методов встраивания стойких ЦВЗ для всех типов цифровых данных, защита глубоких моделей имеет некоторые особенности, требующие разработки новых подходов к внедрению защитной информации:

• 1)    процедура встраивания ЦВЗ не должна нарушать точность прогнозов модели при решении исходной задачи;

• 2)    необходимо, чтобы процедура верификации давала положительный результат только в случае, если в модель встроен уникальный ЦВЗ законного владельца;

• 3)    процедура встраивания ЦВЗ должна требовать как можно меньше вычислительных ресурсов.

Первый метод решения проблемы защиты авторских прав на нейронные сети был опубликован в 2017 году [1], и с этого момента актуальность задачи встраивания ЦВЗ в модели глубокого обучения только растет [2, 3]. Существующие методы встраивания ЦВЗ в модели глубокого обучения реализуются в зависимости от доступности параметров модели на этапе верификации.

Согласно white-box подходу к встраиванию [1, 4– 7] ЦВЗ встраивается путем непосредственного изменения параметров модели, которые, соответственно, должны быть доступны на этапе верификации. Например, в [6] заданный набор параметров подвергается дискретному косинусному преобразованию.

Поскольку веса украденной модели чаще всего не доступны, большинство известных методов реализуют принцип black-box [8– 17] встраивания ЦВЗ, согласно которому проверка наличия встроенной информации производится путем подачи запросов к модели и оценки ее прогнозов. Таким образом, факт нарушения авторских прав может быть подтвержден без доступа к параметрам модели и незаметно для злоумышленника. Процедура встраивания ЦВЗ выполняется путем обучения модели на выборке данных, которая содержит образцы-триггеры, размеченные таким образом, чтобы прогноз модели с ЦВЗ отличался от прогноза исходной модели. Встраивание считается успешным, если после обучения обеспечивается высокая точность прогнозов при подаче на вход модели с ЦВЗ образцов-триггеров из верификационной выборки (т.е. заданного набора изображений, который используется для подтверждения авторских прав). При этом результаты прогноза должны быть уникальными и соответствовать только ЦВЗ легального пользователя. Таким образом, задача blackbox встраивания ЦВЗ заключается прежде всего в создании набора триггеров, обеспечивающего достоверность верификации.

Более подробный обзор методов встраивания ЦВЗ в глубокие нейронные сети представлен автором настоящей статьи в работе [18].

В данной работе предлагается метод black-box встраивания ЦВЗ в глубокие модели классификации изображений, ключевая идея которого заключается в синтезе набора триггеров путем построения псевдо-голографических изображений (псевдоголограмм) [19] на основе бинарных последовательностей и наложения их на изображения исходного датасета.

Идея формирования псевдоголограмм для формирования триггеров уже применялась ранее в [18]. Отличие двух разработанных авторами методов заключается в процедуре формирования триггерной выборки, которая, как было отмечено выше, в большей степени определяет методы black-box встраивания ЦВЗ. В настоящей работе триггеры формируются путем «наложения» сгенерированных полутоновых псевдоголограмм на растровые изображения исходного набора данных с помощью аддитивной стратегии встраивания ЦВЗ. В работе [18] в качестве триггеров синтезируются цветные псевдоголограммы, представляющие собой объединение трех полутоновых псевдоголограмм: все три псевдоголограммы имеют одинаковое расположение импульсов спектра, но значения этих импульсов задаются случайным образом для каждого полутонового изображения с помо- щью генератора псевдослучайных чисел (ГПСЧ), что приводит к фазовому сдвигу двумерных синусоид и соответственно обеспечивает разнообразие значений яркости для R-, G- и B-каналов выходного цветного изображения. При этом цветные псевдоголограммы не встраиваются в изображения исходного набора данных, а служат триггерами сами по себе.

Метод [18] требует строгого контроля параметров генератора псевдослучайных чисел (ГПСЧ), используемого при задании значений импульсов комплексного спектра, поскольку подразумевает неповторимость псевдоголограмм в обучающей выборке. Такой подход может рассматриваться как способ аугментации данных, обеспечивающий разнообразие псевдоголограмм в обучающей выборке и, как следствие, лучшую генерализацию модели при встраивании ЦВЗ. Соответственно, одним из ключевых этапов проведенной работы являлся поиск и формализованное описание ограничений, накладываемых на параметры ГПСЧ.

Метод, представленный в данной работе, также подразумевает применение различных псевдоголограмм, «накладываемых» на изображения оригинального датасета, но количество генерируемых псевдоголограмм может быть меньше, чем размер всей триггерной выборки, то есть одну и ту же псевдоголограмму допустимо повторно встраивать в различные изображения оригинального датасета. Вариативность выборки достигается здесь не за счет псевдоголограмм, а за счет многообразия изображений оригинального датасета, на который они накладываются.

Таким образом, одной из задач, поставленных при разработке предлагаемого в данной работе метода, являлась задача анализа влияния областей и стратегий встраивания псевдоголограмм в изображения при формировании триггеров на качество встраивания ЦВЗ в глубокие модели, которое приведено авторами в работе [20]. Для того чтобы идеи исследования [20] могли быть применены в решении задачи защиты авторских прав, необходимо проанализировать предлагаемый подход к формированию триггеров не только на моделях бинарной классификации, но и на моделях мультиклассовой классификации, а также провести исследование результирующего метода встраивания ЦВЗ по всем критериям качества, выдвигаемым к методам защиты авторских прав на глубокие модели, и произвести подбор параметров, при которых эти критерии выполняются. Результаты, полученные в рамках решения перечисленных задач, представлены в настоящей статье.

Кроме того, согласно результатам экспериментальных исследований, предложенный в данной работе метод встраивания ЦВЗ имеет ряд преимуществ в сравнении с методом [18], а именно:

• 1)    обеспечивает более высокую точность моделей мультиклассовой классификации после встраивания ЦВЗ;

• 2)    демонстрирует больший показатель информационной емкости;

• 3)    требует меньше вычислительных ресурсов.

1.    Предлагаемый метод встраивания ЦВЗ

Для формирования триггерной выборки предлагается использовать набор искусственно синтезируемых изображений, кодирующих двоичную последовательность заданной длины в виде синусоидальных функций и называемых псевдоголограммами. Такие изображения формируются на основе синтеза комплексного спектра путем размещения импульсов на двумерной комплексной плоскости в спектральной области в зависимости от некоторой двоичной последовательности S . Соответственно, с помощью обратного дискретного преобразования Фурье каждый бит последовательности S будет отображен на итоговом изображении в форме двумерной синусоиды. Подробное описание и исследование алгоритмов синтеза и анализа псевдоголограмм приведено в работе [19].

Триггеры формируются путем наложения псевдоголограмм на растровые изображения исходного набора данных с помощью аддитивной стратегии встраивания ЦВЗ. Метка класса изображения-триггера определяется не исходной меткой изображения, на которое наложена псевдоголограмма, а меткой последовательности, скрытой в псевдоголограмме. Далее к объектам-триггерам добавляются исходные изображения оригинального датасета с исходной разметкой, формируя таким образом датасет для встраивания ЦВЗ. Далее защищаемая модель обучается на полученном наборе изображений до тех пор, пока не будет достигнута заданная точность на верификационной выборке.

Генерация набора псевдоголограмм

Формирование набора псевдоголограмм для последующего встраивания и верификации производится следующим образом: для каждого класса модели генерируется уникальная бинарная последовательность длины l . Таким образом будет сгенерировано k последовательностей S 1, S 2,..., S i ,..., S k , где k - это общее число классов, распознаваемых защищаемой моделью.

Следующим шагом является генерация псевдоголограмм на основе каждой из последовательностей. Согласно подходу, предложенному в [19], псевдоголограмма формируется как отображение последовательности S в двумерное пространство путем расстановки спектральных импульсов на двух кольцах с радиусами r и r + Δr в порядке, задаваемом битами последовательности. Параметры радиусов зависят от длин последовательности: r = 0,36 × l; Δr = 6. При этом, если задавать спектральным компонентам случайные значения, то псевдоголограммы, сгенерированные на основе одной и той же последовательности, будут незначительно отличаться с каждой новой генерацией. Применительно к решаемой задаче это позволит увеличить вариативность выборки внутри одного класса и соответственно повысить стойкость к fine-tuning атакам. В то же время псевдоголограммы, сгенерированные на основе различных последовательностей, имеют значительные визуальные отличия. Соответственно, такие псевдоголограммы целесообразно относить к разным классам.

Таким образом, после синтеза n псевдоголограмм на основе каждой из последовательностей будет получен набор из n × k изображений. Далее в зависимости от кодируемой последовательности каждой псевдоголограмме назначается метка класса: псевдоголограмме, кодирующей последовательность S i , назначается метка i -го класса.

Полученный набор псевдоголограмм используется как на этапе построения набора триггеров, так и на этапе верификации модели со встроенным ЦВЗ. Примеры псевдоголограмм, сгенерированных для одного класса, представлены на рис. 1.

Формирование триггерной выборки

Триггерная выборка формируется на основе сгенерированных псевдоголограмм путем их «наложения» на изображения исходного набора данных, используемых в процессе обучения модели-контейнера.

Рис. 1. Набор псевдоголограмм на основе одной бинарной последовательности

В работе [20] авторами настоящей статьи проведен подробный сравнительный анализ различных комбинаций стратегий и областей встраивания ЦВЗ в изображения с целью выявления подходов, которые могут применяться для формирования триггерных выборок на основе псевдоголограмм.

В качестве исследуемых стратегий встраивания ЦВЗ в изображения были выбраны следующие: встраивание в заданные битовые плоскости [21], когда выбранные плоскости изображения-контейнера заменяются на биты ЦВЗ, и аддитивное встраивание [22], когда изображение ЦВЗ, умноженное на параметр видимости, складывается с изображением-контейнером. В первом случае варьируемым параметром является число младших битовых плоскостей изображения, которые будут заменены старшими битовыми плоскостями ЦВЗ. Во втором случае параметром является положительный коэффициент q , регулирующий видимость ЦВЗ.

С точки зрения областей встраивания все существующие методы встраивания ЦВЗ в изображения подразделяются на методы встраивания в простран- ственной области, когда ЦВЗ внедряется непосредственно в пиксели изображения-контейнера, и методы встраивания в области преобразования, когда ЦВЗ встраивается в коэффициенты заданного разложения изображения-контейнера. Здесь в качестве исследуемых в рамках эксперимента областей встраивания были рассмотрены два цветовых пространства – RGB и YCbCr (как подходы к встраиванию в пространственную область) и коэффициенты дискретного вейвлет-преобразования (ДВП) Хаара (как один из подходов к встраиванию в область преобразования).

Таким образом, для каждой комбинации стратегии, области и параметра встраивания был сгенерирован уникальный обучающий набор, содержащий триггеры. Далее проводилось обучение исследуемых моделей на каждом из полученных наборов.

Согласно результатам, полученным в работе [20], наилучшим алгоритмом встраивания псевдоголограмм в изображения оригинального датасета, позволяющим успешно встраивать ЦВЗ в модели глубокого обучения, является алгоритм аддитивного встраивания в пространственную область изображения. Такая комбинация области встраивания и стратегии построения набора триггеров позволяет достичь наиболее высокой эффективности встраивания ЦВЗ в глубокие модели, а именно одновременно достичь высокую точность верификации ЦВЗ и сохранить исходную точность решения основной задачи классификации.

В данной работе встраивание псевдоголограммы в пространственную область изображения осуществляется путем перехода в цветовое пространство YCbCr и выбора компоненты яркости Y. Сначала размер матрицы Y приводится к размеру встраиваемой псевдоголограммы. Далее псевдоголограмма встраивается в Y-компоненту согласно аддитивной стратегии встраивания ЦВЗ с выбранными параметрами:

ˆ

Y N X N ^— Y N X N + P ^X q ,

где Y N × N . – Y-компонента, P – встраиваемая псевдоголограмма; q – параметр видимости, Ŷ N × N – результирующее изображение.

Полученный результат приводится к стандартному диапазону значений яркости Y-компоненты [16, 235] путем минимаксной нормализации, после чего преобразуется к исходным размерам. Далее изображение с наложенной псевдоголограммой конвертируется обратно в цветовое пространство RGB.

На рис. 2 представлены примеры изображений с наложенной псевдоголограммой для датасета CIFAR-100.

Встраивание ЦВЗ в модель

Для встраивания ЦВЗ в модель необходимо сформировать соответствующий датасет (далее – датасет для встраивания ЦВЗ). Для этого случайным образом выбирается заданное количество изображений оригинального датасета.

Рис. 2. Примеры изображений-триггеров, сформированных на основе датасета CIFAR-100

Каждое изображение добавляется в обучающую выборку дважды: со встроенной случайно выбранной псевдоголограммой и без. При этом оригинальным изображениям без встроенных псевдоголограмм соответствуют исходные метки классов, а изображениям-триггерам метки назначаются в зависимости от того, какая последовательность закодирована в наложенной псевдоголограмме. Процедура формирования триггерной выборки приведена на рис. 3.

Класс «Лошадь»

Псевдоголограммы

Исходные изображения

Рис. 3. Формирование триггерной выборки

Изображения-триггеры

Далее в полученный набор добавляется заданное количество случайных изображений оригинального датасета, которые не использовались в процессе построения триггерной выборки. Результирующий набор изображений представляет собой датасет для встраивания ЦВЗ, на котором будет производиться обучение защищаемой глубокой модели.

Для оценки эффективности процедуры встраивания ЦВЗ, а также для дальнейшей проверки авторских прав на модель необходимо построить верификационную выборку, в качестве которой предлагается использовать набор исходных полутоновых псевдоголограмм (т.е. не встроенных в изображения оригинального датасета). Заметим, что хранить данную выборку нет необходимости: псевдоголограммы могут быть сгенерированы заново на основе набора последовательностей, используемого при формировании триггеров.

Будем считать, что процедура встраивания ЦВЗ выполнена успешно, если достигнута высокая точность модели на верификационной выборке, и при этом точность решения исходной задачи классификации на тестовой выборке оригинального датасета сохраняется или падает незначительно.

Схема встраивания ЦВЗ в модель приведена на рис. 4.

Набор для встраивания ЦВЗ

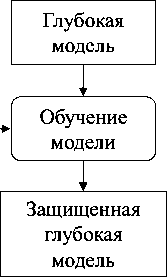
Рис. 4. Встраивание ЦВЗ в модель

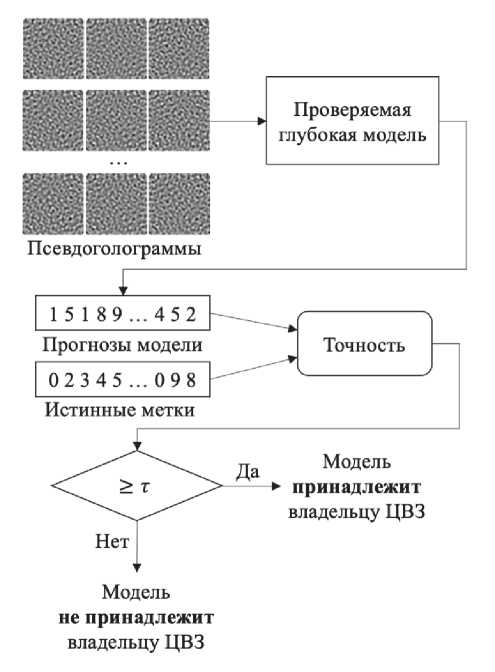
Верификация модели со встроенным ЦВЗ

Для подтверждения авторских прав путем проверки наличия встроенного ЦВЗ нужен только доступ к прогнозам предположительно украденной модели. Правообладателю необходимо подать на вход модели псевдоголограммы верификационной выборки и оценить точность классификации путем сравнения прогнозируемых классов и меток, заданных на этапе встраивания ЦВЗ.

Схема верификации ЦВЗ представлена на рис. 5.

Псевдоголограммы

Модель не принадлежит владельцу ЦВЗ

Прогнозы модели

Истинные метки

Модель

* принадлежит владельцу ЦВЗ

Нет

Проверяемая глубокая модель

Точность

1 5 1 8 9 ... 4 5 2

023 45 ... 098

Рис. 5. Процедура верификации ЦВЗ

Если точность верификации достигает значения заданного порога т, то правообладатель может заявить о факте несанкционированного распространения интеллектуальной собственности. В данной статье мы полагаем т = 0,9, то есть если точность на верификационной выборке лежит в диапазоне [0,9; 1,0], то можно сделать заключение, что модель принадлежит владельцу ЦВЗ. Кроме того, если значение точности лежит в диапазоне [т - Ат; т], то с высокой вероятностью модель также принадлежит владельцу ЦВЗ, но при этом модель была модифицирована, например, с целью удаления ЦВЗ. Значение Ат может быть оценено путем экспериментальной оценки максимальной доли ложноположительных результатов модели (false positive rate, FPR ): т - Ат > max FPR .

• 2.    Исследование эффективности предложенного метода встраивания ЦВЗ Подготовка моделей и данных

Для проведения экспериментального исследования было подготовлено 5 моделей-контейнеров для встраивания ЦВЗ с архитектурами MobileNetV2, Inception-v3, DenseNet121, VGG16 и Resnet50. Разнообразие блоков в составе данных архитектур, а также различие в количестве параметров и скорости обучения позволит в достаточной мере оценить применимость предлагаемого метода для защиты глубоких моделей-классификаторов. Для формирования кон- тейнеров для встраивания ЦВЗ предобученные модели из библиотеки pytorch-hub [23] были обучены на двух датасетах: CIFAR-10 и CIFAR-100 [24], включающих 10 и 100 классов соответственно. Каждый датасет содержит 50000 обучающих и 10000 тестовых изображений, при этом в каждом классе содержится одинаковое количество изображений.

В обоих случаях были выбраны следующие гиперпараметры:

• •    Learning rate: 0,001.

• •    Функция ошибки: кросс-энтропия.

• •    Метод оптимизации: стохастический градиентный спуск с momentum = 0,9.

• •    Число эпох: 50.

• •    Размер батча: 64.

В результате было получено 5 моделей, обученных на наборе CIFAR-10, и 5 моделей, обученных на наборе CIFAR-100.

Для случая 10 классов оценивались метрики точности моделей acc test на тестовой выборке CIFAR-10 и на верификационной выборке из 1000 псевдоголограмм acc ver (100 псевдоголограмм на класс). Метрика acc test рассчитывается как доля верно классифицированных тестовых изображений оригинального датасе-та и демонстрирует точность решения моделью исходной задачи классификации, в то время как метрика acc ver отражает точность классификации псевдоголограмм и вычисляется для оценки качества встраивания ЦВЗ в модель.

Для случая 100 классов оценка acc test производилась на тестовой выборке CIFAR-100, а оценка acc ver – на наборе из 10000 псевдоголограмм (100 псевдоголограмм на класс).

Полученные показатели точности подготовленных моделей-контейнеров отражены в табл. 1.

Табл. 1. Значения точности моделей-контейнеров

Модель	CIFAR-10		CIFAR-100
	acc test	acc ver	acc test	acc ver
mobilenet	0,9499	0,100	0,7974	0,0064
inception	0,9708	0,041	0,8344	0,0116
resnet	0,9631	0,100	0,8316	0,0104
densenet	0,9680	0,113	0,8328	0,0112
vgg	0,9402	0,104	0,7703	0,0060

Стоит заметить, что модели-контейнеры не содержат встроенного ЦВЗ: точность на верификационном наборе псевдоголограмм была оценена с целью продемонстрировать тот факт, что ЦВЗ не может быть ложно распознан в модели без ЦВЗ.

Для встраивания ЦВЗ в модели-контейнеры были сгенерированы триггерные выборки на основе дата-сетов CIFAR-10 и CIFAR-100.

Для случая 10 классов сначала были сгенерированы 10 уникальных бинарных последовательностей длины l =30. Далее было синтезировано 3 набора псевдоголограмм: по 100, 250 и 500 изображений для каждого класса, что составляет 0,02, 0,05 и 0,1 от общего размера обучающей выборки CIFAR-10 соответственно.

Для случая 100 классов сначала были сгенерированы 100 уникальных бинарных последовательностей длины l =30, на основе которых синтезировались наборы псевдоголограмм: по 10, 25 и 50 псевдоголограмм на каждый класс, что составляет 0,02, 0,05 и 0,1 от общего размера обучающей выборки CIFAR-100 соответственно.

В обоих случаях датасеты для встраивания ЦВЗ формировались путем выбора случайных изображений из набора CIFAR-10/CIFAR-100 и встраивания соответствующих псевдоголограмм в Y-компоненту цветового пространства YCbCr с параметром видимости ЦВЗ q = 1. Помимо изображений-триггеров и их оригиналов, датасет для встраивания ЦВЗ далее дополнялся заданным количеством изображений дата-сета CIFAR-10/CIFAR-100, которые не использовались для построения триггеров.

Следует отметить, что при подготовке моделей-контейнеров обучающая выборка подвергалась случайным преобразованиям кадрирования и отражения по центральным осям. Однако при встраивании ЦВЗ случайные преобразования применялись только для изображений оригинального датасета и не применялись для триггеров.

Верификационная выборка в каждом случае представляет собой набор исходных псевдоголограмм, используемых при формировании триггеров.

Выбор параметров встраивания ЦВЗ

Одним из основных требований к методам встраивания ЦВЗ в модели глубокого обучения является сохранение точности прогнозов модели при решении исходной задачи классификации.

Для одновременного достижения высокой точности верификации ЦВЗ, а также сохранения точности классификации на тестовой выборке необходимо определить параметры встраивания ЦВЗ путем нахождения баланса между количеством оригинальных и триггерных изображений в обучающей выборке.

Для проведения экспериментального исследования были построены наборы для встраивания ЦВЗ, состоящие из различных комбинаций числа триггеров (2, 5 и 10% случайно выбранных изображений из обучающей выборки датасета CIFAR-10/CIFAR-100 с наложенными псевдоголограммами) и числа оригинальных изображений (10, 20 и 30% случайно выбранных изображений из обучающей выборки дата-сета CIFAR-10/CIFAR-100). Заметим, что в подмножество оригинальных изображений входят в том числе оригиналы изображений, используемых при формировании триггеров. Также заметим, что в данной работе в каждый класс добавлялось одинаковое коли- чество изображений (все формируемые выборки сбалансированы).

Эксперименты проводились на модели архитектуры mobilenet. Встраивание проводилось в течение 50 эпох. Гиперпараметры обучения совпадают с выбранными для моделей-контейнеров. В результате эксперимента для каждой комбинации параметров выбиралась модель с наилучшим показателем точности на тестовой выборке при условии достижения заданного порога точности верификации ЦВЗ. Результаты эксперимента, проведенного на наборе CIFAR-10 , отражены в табл. 2 и 3.

Табл. 2. Точность acc test моделей со встроенным ЦВЗ на тестовой выборке (CIFAR-10)

Доля оригинальных изображений Доля триггеров	10%	20%	30%
2%	0,9480	0,9496	0,9519
5%	0,9461	0,9491	0,9516
10%	0,9405	0,9486	0,9500

Табл. 3. Точность acc ver моделей со встроенным ЦВЗ на верификационной выборке (CIFAR-10)

Доля оригинальных изображений Доля триггеров	10%	20%	30%
2%	1,0000	0,9990	1,0000
5%	0,9996	1,0000	1,0000
10%	0,9978	0,9994	1,0000

Согласно полученным результатам, наиболее высокая точность как на тестовой, так и на верификационной выборке достигается, когда датасет для встраивания ЦВЗ содержит оригинальные изображения в количестве 30 % от исходного датасета CIFAR-10 и изображения-триггеры в количестве 2 % от исходного датасета CIFAR-10.

Результаты эксперимента, проведенного на наборе CIFAR-100 , отражены в табл. 4 и 5.

Табл. 4. Точность acc test моделей со встроенным ЦВЗ на тестовой выборке (CIFAR-100)

Доля оригинальных изображений Доля триггеров	10 %	20%	30%
2	0,7541	0,7693	0,7695
5	0,7655	0,7765	0,7782
10	0,7563	0,7726	0,7748

Согласно результатам эксперимента наилучшее соотношение оригинальных и триггерных изображений составляет 30 % и 5% от исходного набора данных CIFAR-100 соответственно. Такой выбор параметров позволяет как успешно встроить ЦВЗ в модель, так и сохранить метрику качества решения основной задачи на исходном уровне.

Табл. 5. Точность acc ver моделей со встроенным ЦВЗ на верификационной выборке (CIFAR-100)

Доля оригинальных изображений Доля триггеров	10 %	20%	30%
2%	0,7770	0,7110	0,6820
5%	0,9824	0,9944	0,9924
10%	0,9996	0,9994	0,9912

Заметим, что в работе [18] сохранение исходной точности модели на тестовой выборке достигалось за счет использования при встраивании ЦВЗ большего размера батча, чем при обучении модели-контейнера. Однако согласно результатам настоящего эксперимента предлагаемый в данной работе метод обеспечивает сохранение исходной точности классификации даже при встраивании ЦВЗ с тем же размером батча, что и у модели-контейнера. Иногда этот факт может существенно повлиять на применимость метода, например, если у владельца модели имеются ограниченные вычислительные ресурсы либо когда модель изначально была обучена с высоким значением данного гиперпараметра. Таким образом, предлагаемый метод обеспечивает более высокую точность классификации при меньших вычислительных затратах.

Выбор параметров формирования триггерной выборки

Целью данного эксперимента является исследование параметров формирования псевдоголограмм на результат встраивания ЦВЗ в модели глубокого обучения. Исследуемым параметром является длина последовательностей, закодированных в синтезируемых псевдоголограммах.

В процессе подготовки данных для эксперимента были сформированы наборы псевдоголограмм для различных значений д лины последовательности l :

• -    для CIFAR-10 l -1 0,90 с ш агом 20;

• -    для CIFAR-100 l -10,100 с шагом 10.

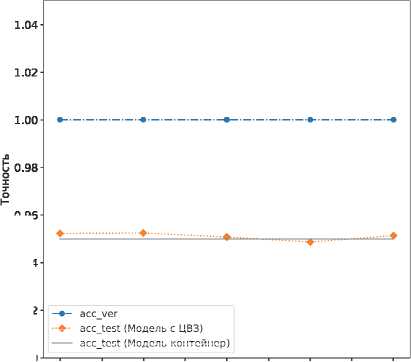
На основе всех сформированных наборов псевдоголограмм были сгенерированы датасеты для встраивания ЦВЗ с наилучшими параметрами, полученными в предыдущем эксперименте. Далее модели-контейнеры архитектуры mobilenet обучались на сформированных наборах для встраивания ЦВЗ в течение 50 эпох. В каждом случае были оценены значения acc test на тестовой выборке оригинального датасе-та CIFAR-10/CIFAR-100 и на верификационной выборке исходных псевдоголограмм acc ver . Результаты эксперимента приведены на рис. 5.

Согласно полученным результатам в случае 10 классов параметр длины последовательности l практически не влияет на результат встраивания ЦВЗ. Однако при увеличении числа классов до 100 при l >60 качество встраивания ЦВЗ начинает ухудшаться как с точки зрения точности на тестовой выборке acctest, так и точности на этапе верификации ЦВЗ accver. Это обусловлено тем, что при увеличении l возрастает частота двумерных синусоид псевдоголограммы, и для их точного распознавания требуется большее количество триггеров в обучающей выборке. Наилучший результат на наборе CIFAR-100 был получен при l =30 с точностью acctest = 0,7805 и accver = 0,9976.

1.00

U 0.98

■♦■ асе test (модель с цвз)

--- асе test (Модель-контейнер)

0.96

0.94

0.92

0.90 10    20    30    40    50    60    70    80    90

a)

Длина бинарной последовательности

20         40         60         80        100

Длина бинарной последовательности

б)

Рис. 6. Точность модели после встраивания ЦВЗ с различными значениями l: а) CIFAR-10; б) CIFAR-100

Заметим, что для датасета CIFAR-100 точность верификации превышает заданный порог acc ver > 0,9 при l < 80, тогда как в результате аналогичного эксперимента, проведенного для метода [18], максимальный параметр длины последовательности, при котором точность верификации находится в допустимом диапазоне, равен l =60. Соответственно, отсюда следует вывод, что в сравнении с [18] предложенный в настоящей работе метод встраивания ЦВЗ обладает преимуществом по критерию информационной емкости.

Исследование применимости для различных архитектур глубоких моделей

Эксперимент направлен на исследование эффективности предложенного метода с точки зрения при- менимости ко всем выбранным архитектурам моделей глубокого обучения. Эксперимент заключался во встраивании ЦВЗ в модели-контейнеры и оценке точности на тестовой выборке acctest и точности на этапе верификации ЦВЗ accver.

Размеры обучающих датасетов для встраивания ЦВЗ выбраны согласно лучшим результатам предыдущих экспериментов:

– датасет на основе CIFAR-10 содержит оригинальные изображения в количестве 30% и изображения-триггеры ( l =30) в количестве 2% от исходного датасета;

– датасет на основе CIFAR-100 содержит оригинальные изображения в количестве 30% и изображения-триггеры ( l =30) в количестве 5% от исходного датасета.

Гиперпараметры обучения совпадают с выбранными для моделей-контейнеров.

Также в данном эксперименте была оценена точность верификации на двух случайных наборах псевдоголограмм, отличных от верификационного набора правообладателя. Для каждого набора были синтезированы псевдоголограммы на основе k случайно сгенерированных последовательностей длины l = 30. Результаты проведенных экспериментов приведены в табл. 6-7. Точность верификации на случайных наборах псевдоголограмм обозначена как acc_ran d1 и acc rand2 .

Табл. 6. Эффективность предлагаемого метода для различных архитектур (CIFAR-10)

Модель	acc test	acc ver	acc rand1	acc rand2
mobilenet	0,9519	1,0	0,0988	0,0472
inception	0,9722	1,0	0,1020	0,1514
resnet	0,9651	1,0	0,1548	0,1970
densenet	0,9692	1,0	0,1188	0,2156
vgg	0,9429	1,0	0,0292	0,1070

Табл. 7. Эффективность предлагаемого метода для различных архитектур (CIFAR-100)

Модель	acc test	acc ver	acc rand1	acc rand2
mobilenet	0,7805	0,9976	0,0216	0,0080
inception	0,8322	0,9940	0,0088	0,0216
resnet	0,8330	0,9852	0,0112	0,0092
densenet	0,8266	0,9876	0,0088	0,0176
vgg	0,7724	0,9972	0,0276	0,0156

Согласно результатам в табл. 6, 7, почти все модели сохраняют исходное значение точности на тестовом наборе, в то время как точность на верификации выше 0,98. Исключение составляет незначительное (менее чем на 0,02) падение acc test для моделей архитектур mobilenet и densenet, предобученных на дата-сете CIFAR-100.

Кроме того, результаты подачи на вход моделей с ЦВЗ двух случайных наборов псевдоголограмм показывают, что вероятность ложноположительной верификации псевдоголограмм, не принадлежащих законному владельцу, крайне мала.

3.    Исследование стойкости к злоумышленным атакам

Fine-tuning атака

Одним из возможных способов удаления встроенного ЦВЗ из модели без существенной потери качества является атака на основе fine-tuning, заключающаяся в переобучении модели на датасете, который может отличаться от исходного. Настоящий эксперимент направлен на исследование устойчивости встроенных ЦВЗ к подобным атакам.

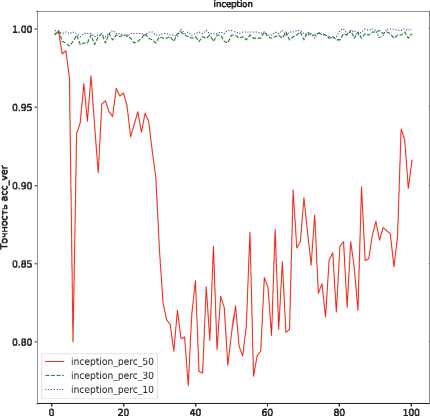
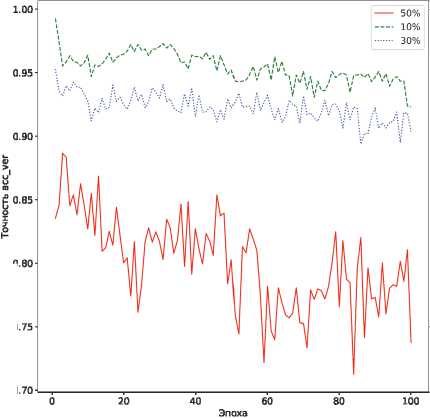
Симуляция атаки проводилась путем тюнинга модели архитектуры inception-v3 на датасете, состоящем из 10, 30 и 50% случайно выбранных изображений тестовой выборки CIFAR-10 / CIFAR-100, в течение 100 эпох. Гиперпараметры обучения совпадают с выбранными для моделей-контейнеров и моделей со встроенными ЦВЗ. На каждой эпохе вычислялась точность модели на верификационном наборе псевдоголограмм. Результаты эксперимента представлены на рис. 7.

а)

Эпоха

inception

б)

Рис. 7. Точность верификации ЦВЗ после fine-tuning атаки: а) CIFAR-10; б) CIFAR-100

Согласно данным на рис. 7, после обучения на новом наборе данных в течение 100 эпох встроенные ЦВЗ все еще могут быть верифицированы с достаточно высокой точностью. Таким образом, можно сделать вывод о том, что предложенный метод является стойким к атакам на основе fine-tuning.

Pruning атака

Pruning атака заключается в регуляризации модели путем удаления некоторой части ее параметров (то есть весов). Такая атака может привести к снижению возможности модели выделять некоторые признаки для дальнейшей классификации.

Предлагаемый метод встраивания ЦВЗ должен обладать устойчивостью к pruning атакам, т.е. после удаления части параметров модель должна либо сохранить возможность верификации ЦВЗ на уровне, достаточном для подтверждения авторских прав, либо в случае удаления встроенного ЦВЗ качество решения исходной задачи классификации с большой долей вероятности должно существенно снизиться.

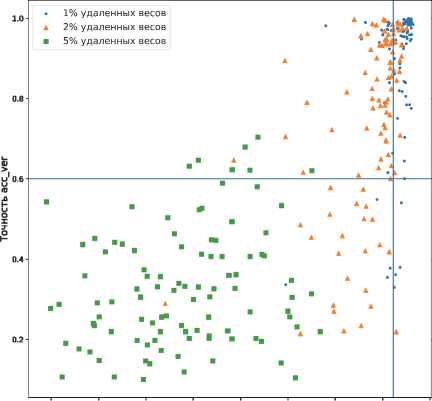
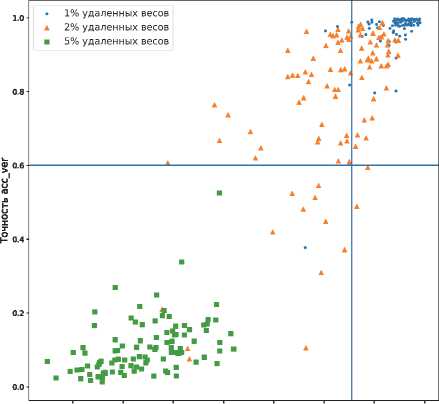
Данный эксперимент заключался в проведении 100 pruning-атак на модель со встроенным ЦВЗ: 1, 2 и 5 % случайно выбранных весов сверточных и полносвязных слоев были удалены. Далее для полученной модели оценивались метрики точности на верификационной и тестовой выборках. Эксперимент проведен на моделях архитектуры inception-v3 для случаев 10 и 100 классов.

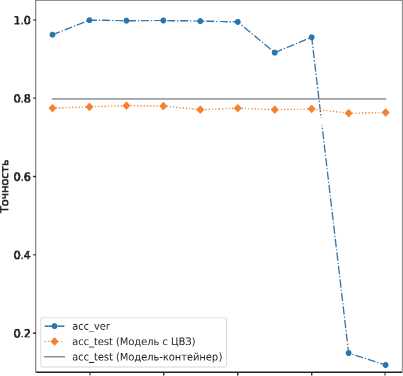
Результаты симуляции pruning атаки продемонстрированы на рис. 8.

Горизонтальная линия показывает порог, при котором все еще можно заявить о наличии встроенного ЦВЗ. Если точность верификации ниже 0,6, мы полагаем, что ЦВЗ был полностью удален. Вертикальная линия показывает порог точности решения исходной задачи классификации. Будем считать, что допустимое падение точности модели с ЦВЗ на тестовой выборке после атаки составляет не больше 0,05.

Как видно из рис. 8, после проведенной серии атак в большинстве случаев либо сохраняется возможность корректной верификации ЦВЗ, либо происходит значительное падение точности на тестовой выборке. Следовательно, модель окажется непригодной для использования при попытке удаления ЦВЗ. Случаи успешных атак составляют сравнительно малую долю от общего числа атак (1,6 % для CIFAR-10 и 0,6% для CIFAR-100). Таким образом, можно сделать вывод о том, что предложенный метод является стойким к pruning атакам.

Заключение

В статье предложен метод защиты авторских прав на глубокие модели классификации изображений. Ключевая идея предложенного метода black-box встраивания ЦВЗ заключается в формировании триггерной выборки путем синтеза и наложения псевдо- голограмм на изображения оригинального датасета. Показано, что предлагаемый метод позволяет сохранить исходную точность модели, при этом модели, не принадлежащие владельцу ЦВЗ, не могут быть ложно верифицированы.

inception

a)

Точность acctest

Рис. 8. Точность верификации ЦВЗ после pruning атаки: а) CIFAR-10; б) CIFAR-100

• б)

Экспериментальные исследования включают оценку эффективности встраивания ЦВЗ в глубокие модели различных архитектур, а также анализ влияния параметров формирования обучающей выборки на точность защищаемых моделей. Кроме того, согласно результатам экспериментов встроенные ЦВЗ являются стойкими к попыткам злоумышленного удаления путем дообучения (fine-tuning) или обрезки параметров (pruning) модели.

Исследование выполнено за счет гранта Российского научного фонда № 21-71-00106,