Затухание вынужденных колебаний и гидроударных волн в турбулентном потоке протяжённых трактов систем питания жидкостных ракетных двигателей

Введение. Разработанные в 1980-х гг. маршевые жидкостные ракетные двигатели (ЖРД) РД 170 и РД 171 для ракетоносителей (РН) «Энергия» и «Зенит» на компонентах керосин и жидкий кислород с высоким уровнем тяги (806,4 тс тяги в пустоте) характеризуются значительными расходом компонентов топлива (2393 кг/с) и высоким давлением в камерах сгорания (24,5 МПа). Неизбежное возбуждение ударных волн при открытии или закрытии отсечных клапанов во время проведения испытаний ЖРД сопряжено с повреждением измерительной и управляющей арматуры протяженных магистралей заправки. Одним из основных средств борьбы с гидроударными волнами является установка в магистралях демпферов и других устройств, снижающих энергию ударных возмущений [1–7]. Однако всегда остается открытым вопрос влияния волновых возмущений в магистралях на режим горения в камере ЖРД и, как следствие, возможное возбуждение неустойчивости горения [5; 8].

Из экспериментов на магистралях стендовой системы и теоретически определено, что в случае отсутствия потока ламинарная модель движения жидкости вполне удовлетворительно описывает акустические характеристики тракта в широком диапазоне частот вплоть до пятого резонанса продольных колебаний [1; 2; 9; 10]. Для трактов относительно малой длины (L/D < 200–300) эффектом затухания волновых возмущений при расчётах процессов, протекающих в них, можно пренебречь. Данных об экспериментальных исследованиях распространения волновых возмущений в протяженных трактах (где отношение диаметра к длине 1:1000 и более) в известных публикациях нет. В то же время влияние единичных гидро- ударных волн и волновых процессов на характеристики турбулентных течений в протяженных трактах являются важным аспектом при построении физикоматематических моделей систем питания мощных жидкостных ракетных двигателей [1; 2; 6; 7; 11], а также при моделировании течений и режимов работы магистральных трубопроводов и других задач машиностроения.

Исследование затухания колебаний гидроакустической волны в протяжённых круглых трактах осложнено трудоёмкостью создания экспериментальной установки необходимого масштаба. Именно по этой причине отсутствуют экспериментальные работы, посвященные исследованию процессов затухания волновых возмущений при их распространении в трубах с большим соотношением длины к диаметру. Можно разработать физико-математическую модель распространения волн в турбулентном жидкостном потоке, основываясь на известных классических работах Н. Е. Жуковского [12], Г. Шлихтинга по теории пограничного слоя [13], И. А. Чарного по турбулентным течениям в трубах [14]. Данные для коэффициента трения при ламинарном и турбулентном режимах течения жидкости в гладких каналах можно получить из работ Блазиуса, Халанда, Свами [15] и др. Однако достоверность результатов численных расчетов может быть подтверждена только эмпирическим путем. Учитывая практическую направленность работы, целью настоящего исследования является создание инженерной методики расчета затухания ударных возмущений и вынужденных колебаний в жидкостных турбулентных потоках.

Квазистационарное решение. Определение параметров гидроударной волны и показателя её затухания дал Н. Е. Жуковский в своей работе «О гидравлическом ударе в водопроводных трубах» [12]. Аналитическое решение для коэффициента затухания волны в круглом тракте, полученное из предположения квазистационарности течения, было опубликовано в работе И. А. Чарного в 1975 г. Он, решая задачу распространения волны, использовал метод уравнений характеристик [14]. Представив уравнения для стационарного течения и возмущенного потока, он получил соотношение, связывающее изменение скорости u с пройденной волной расстояния x:

d ² 5 и d x ²

—2 + 1 ю

A p 1

I ю----15 и = 0. риа )

Член в скобках формулы (4) является волновым

2 —2     Ap числом к = ю - i ю——. При относительно малом риа

гидравлическом сопротивлении и достаточно боль

-           _               _                 . - ^{A p} . _ — 2

шой частоте выполняется условие ю--- ^ ю , тогда р иа

—=J

4aD u1

du

X ₀ и 0 | и 0 - X|-X и|и| ’

где а – скорость звука в жидкости; D – внутренний диаметр круглого тракта; X ₀, X - коэффициенты тре-

при решении уравнения (4) вторым слагаемым в волновом числе k можно пренебречь. В полученном решении возмущения давления и скорости при их распространении вдоль тракта зависят от координаты и времени

⁵ p =

ния стационарного и возмущенного течения; u 1 – скорость распространения волны возмущения в сечении x = 0; u – скорость распространения волны возмущения при x > 0; u 0 – стационарная скорость течения до внесения возмущения в сечении x .

Коэффициент трения λ появляется при переходе от двумерного течения к одномерному, когда уже нельзя связать напряжения вязкого трения с изменением профиля скорости. В этом случае гидравлические потери давления из-за трения связывают с изменением скорости эмпирическими зависимостями типа уравнения Блазиуса. В то же время известно, что влияние сил трения жидкости о стенки гидравлического тракта зависит от частоты [12]. Используя безразмерные вариации скорости и давления в виде отношения возмущений скорости и давления 5 и' и 5 p' к их средним

^A a -ю^ A exp i ( ю t - kx ) - B exp i ( ю t + kx ) ] .

_s    5 и' _s    5 p'

стационарным значениям 5и = —, 5p =---, а также uср         pср

t безразмерных времени t =---- и координаты

( l / a )

Уравнение (5) описывает распространение волн постоянной формы от источника в разные стороны трубы. Первое слагаемое в квадратных скобках описывает распространение возмущения в прямом направлении, а второе – в обратном. Постоянные A и B зависят от исходного сигнала возмущения. На практике мы чаще встречаемся с эффектом затухания возмущения, т. е. когда влиянием сил вязкого трения пренебрегать нельзя. В этом случае обе составляющие волнового числа являются соизмеримыми величинами, а решение уравнения (4) приобретает несколько другую форму, в которой появляется дополнительный множитель exp [ - Im( к ) x ] . Для гармонических колебаний, распространяющихся в прямом направлении, возмущения давления записываются следующим образом:

5 p = A exp i ( ю t - kx ) exp [ im ( к ) x ] . (6)

x x = —, уравнения движения жидкости в малых откло нениях можно представить в виде

р иа 55 и d5 p A p

-— + —- + —— 5 и = 0;

p ср ^d t    C x   p ср

55 p + р иа 55 и = о

5 7    p ср 5 x    ,

Мнимая часть комплексного волнового числа является коэффициентом затухания Im ( к ) = П . Значение коэффициента A получим из граничных условий при x = 0, так как в этом случае возмущения равны колебаниям, возбуждаемым источником: A = 5 p ₀.

В экспериментах показатель (декремент) затухания определяем как величину, обратную расстоянию, на котором амплитуда волны уменьшается в e раз:

n = 1ln ^{5 p} 0 = 1ln ^{5 и} >.              (7)

x   5p   x   5 и

где ∆ p – гидравлические потери давления из-за вязкого трения в тракте.

В работе [2] рассмотрен пример распространения возмущений вдоль магистрали. Решая данное уравнение для гармонических колебаний частоты ω (безраз-

® мерный параметр частоты ю = —): a

Для гармонических колебаний в работе [2] аналитически было получено значение декремента затухания

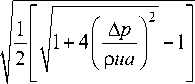
5 p = 5 p o e i ° ^t ;

5 и = 5 и₀ e‘ ^ю t ,

где 5 p ₀ и 5 и₀ - амплитуды вынужденных колебаний давления и скорости, и получено решение в виде

Задачу определения коэффициента затухания для нестационарных течений в гидравлической магистрали можно решить аналитически лишь при специальных допущениях [14]. В общем случае необходимо выполнить точную математическую модель в частных производных и решить полученную систему уравнений численными методами.

В данной работе мы экспериментально исследовали затухание возмущений в узком диапазоне частот от 1 до 10 Гц и определяли зависимость коэффициента затухания от параметров течения в длинной магистрали.

Эксперимент. Волновые колебания в трубе – это распространяющиеся возмущения давления и скорости, которые связаны между собой известной формулой Н. Е. Жуковского. Поскольку измерение скорости потока технологически сложнее измерения давления, то в экспериментах регистрировались стационарные значения давления и пульсации давления равномерно расположенными вдоль трубы датчиками. При длинах трактов в несколько десятков километров, применительно к задачам транспортировки углеводородных топлив по магистральным трубопроводам, точки измерения контролируемых параметров устанавливались на расстоянии 10–20 км в зависимости от длины исследуемого трубопровода. Аналоговый сигнал датчика давления подавался на вход контроллера сбора, обработки информации и преобразовывался АЦП контроллера в цифровой сигнал. Оцифрованный сигнал фиксировался в оперативной памяти устройства, упаковывался и передавался на сервер базы данных, где были собраны в единую базу данных сигналы от всех точек измерений.

При анализе процессов распространения одиночной гидроударной волны в турбулентном потоке тракта мы столкнулись с задачей выделения полезного сигнала (волнового фронта) на фоне постоянного гидродинамического шума. Сам по себе гидродинамический шум представляет собой колебания различных частот, создаваемых работой насосных агрегатов и прочего технологического оборудования. Обрабатывая сигнал, в котором содержится только гидроди- намический шум, можно наблюдать за процессами затухания волновых возмущений в широком спектре частот. В экспериментах инициировалась одиночная ударная волна с амплитудой более чем в 2 раза большей уровня постоянного гидродинамического шума. Гидроударные волны создавались путем отбора жидкости. При этом в ответ на открытие крана (начало отбора) генерировалась волна разрежения, а на закрытие – волна сжатия (рис. 1).

Эксперименты проводились на магистральных трубопроводах круглого сечения, осуществляющих постоянную перекачку углеводородных топлив. Физические характеристики перекачиваемой жидкости и параметры течения по каждому объекту представлены в таблице.

Проведённый спектральный анализ сигнала, измеренный преобразователем избыточного давления ТЖИУ 406, установленным на расстоянии 4 ⋅ 10 4 D _у , показал, что основная часть спектра гидродинамических колебаний находится в частотном диапазоне до 10 Гц (рис. 2). Высокие частоты, генерируемые работой насосных агрегатов, успевают затухать на расстоянии 4 ⋅ 10 4 D _у .

Измеряя амплитуду единичных гидроударных волн, а также и общий уровень гидродинамического шума, состоящего из колебаний частотой до 10 Гц, были получены идентичные картины затухания. Для каждого экспериментального образца протяженного тракта проводилась серия экспериментов по определению снижения пика давления волновых возмущений. Для этого строились кривые зависимости величины амплитуды гидроударной волны δ p от расстояния (рис. 3).

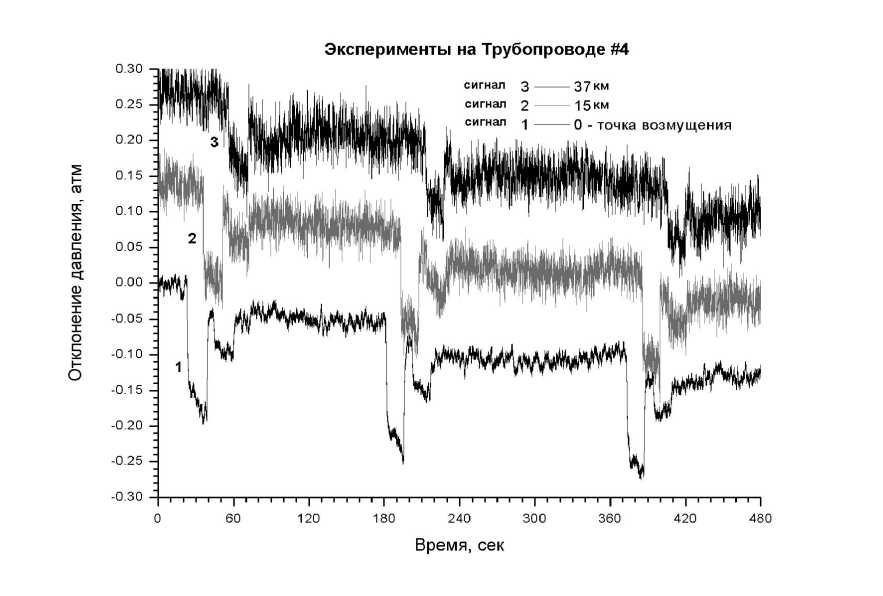
Рис. 1. Измеренные сигналы преобразователей давления, приведённые к отклонениям вблизи 0 вычитанием постоянной составляющей

Характеристики исследуемых объектов

№ п/п	Длина, км	Диаметр, м	Плотность, кг/м 3	Эффективная вязкость, сСт	Скорость течения, м/c	Скорость звука, км/c	Число Рейнольдса (r e ), 105
1	290	1	872,3	21	0,442	1,040	0,21
2.1	23	0,8	864,8	13,4	0,665	1,118	0,39
2.2					1,744	1,103	1,04
3	170	0,5	848	1	1,381	1,161	7,21
4	40	0,5	839,7	2	2,235	1,123	5,47
5	227	0,5	844	6	0,849	1,150	0,85
6	259	1	879	18	1,75	1,060	0,95

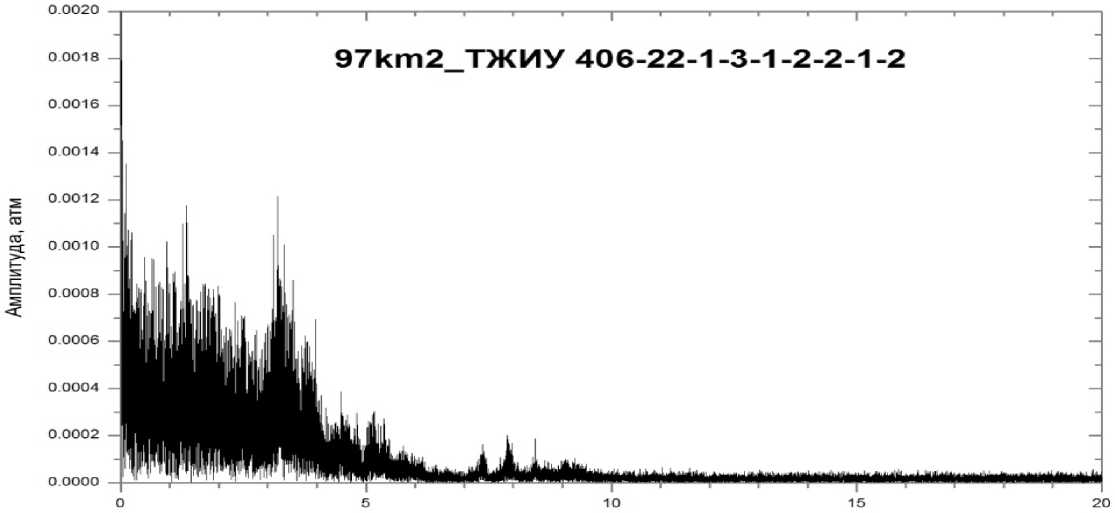
Частота, Гц

Рис. 2. Типичный спектр гидродинамического шума в тракте, записанный преобразователем

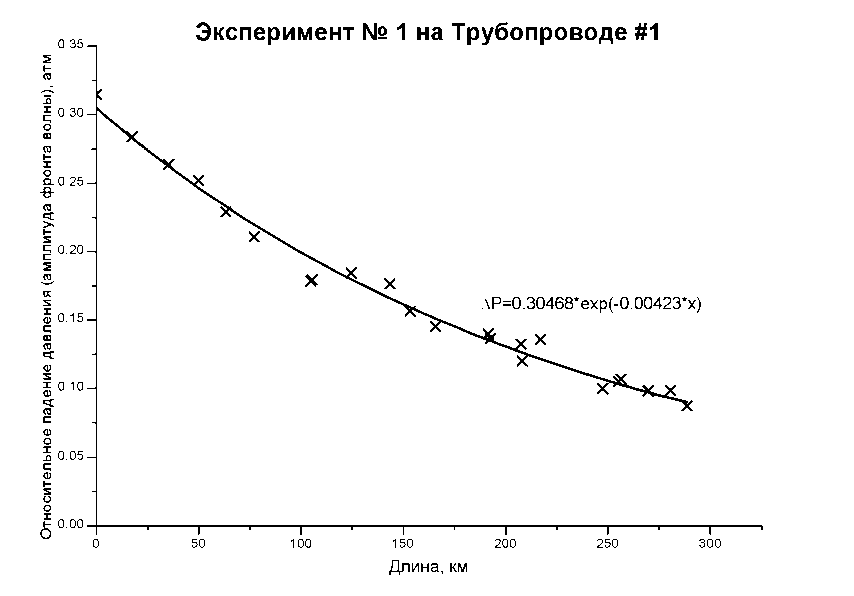
Рис. 3. Процесс затухания одиночной гидроударной волны

Следуя формуле (7), для каждого эксперимента набор точек был аппроксимирован при помощи стандартных функций математического программного обеспечения функцией вида f ( x ) = A exp ( bx ) . Значения коэффициента b являются показателем (декрементом) затухания гидроударной волны. Очевидно, что затухание волновых процессов в турбулентном потоке происходит в основном благодаря силам вязкого трения. Отношение сил трения к силам инерции потока характеризуется числом Рейнольдса. В этой связи представляется целесообразным определять величину декремента затухания одиночной волны в зависимости от числа Рейнольдса:

f -D)n = f (Re ) = f 1-0^ I,             (9)

16v

По =

D _у a

где D _у = const - внутренний диаметр исследуемого тракта; u 0 – cкорость течения принималась постоянной и равной среднему значению скорости; v – вязкость перекачиваемого продукта.

Вычислялась эффективная вязкость по формуле Блазиуса, исходя из уравнения потерь давления на трение на исследуемом участке на стационарном режиме, как

- ¹ 2

A p = 0,3164Re ⁴^-0-. (10) D у 2

На основе обработанных данных всех экспериментов был построен график зависимости коэффициента затухания η от безразмерного параметра Re. Результаты каждой серии экспериментов были обобщены и получено одно среднее значение коэффициента затухания η для каждой серии. Полученные экспериментальные значения коэффициента затухания приведены на рис. 4.

При малых числах Рейнольдса Re << 10 5 течение в пограничном слое становится ламинарным [3] и функция затухания стремится к постоянной величине η 0 , которая может быть вычислена при помощи формулы Стокса для закона трения. Постоянная величина коэффициента волнового затухания в ламинарном потоке равна

При распространении возмущений в потоках при больших числах Рейнольдса динамические изменения происходят внутри ламинарного подслоя. Дальнейшее увеличение числа Рейнольдса не приводит к уменьшению ламинарного подслоя и, следовательно, не даёт изменений в коэффициенте затухания, и в результате он остаётся постоянным и стремится к постоянной величине. Таким образом, искомая функция имеет асимптоту η = а при больших числах Рейнольдса. На основании сделанных предположений экспериментальные точки были аппроксимированы кривой вида

У = По + A [1 - exp (- Bx)].

По результатам проведенной обработки были получены следующие значения для коэффициентов: A = 2 - 10 5 ; B = 10 - 5 .

Запишем полученную зависимость в следующем виде:

П = П о ⁺ e

1 - exp

v ^ReKP I

где P = 47,32 ± 0,32 = 47,3 км - расстояние, на котором сигнал гидроударной волны затухает в е раз в турбулентном пограничном слое, а коэффициент β зависит от толщины ламинарного подслоя, который в свою очередь является функцией от шероховатости стенки магистрали; Re_Kp = ( 0,897 ± 0,022 ) - 10 5 ~ 10 5 -критическое значение числа Рейнольдса, при котором толщина ламинарного подслоя вблизи поверхности трубы становится менее 1 % от диаметра тракта, при этом дальнейший рост потерь из-за вязкого трения постепенно уменьшается, а коэффициент затухания выходит на постоянную величину .

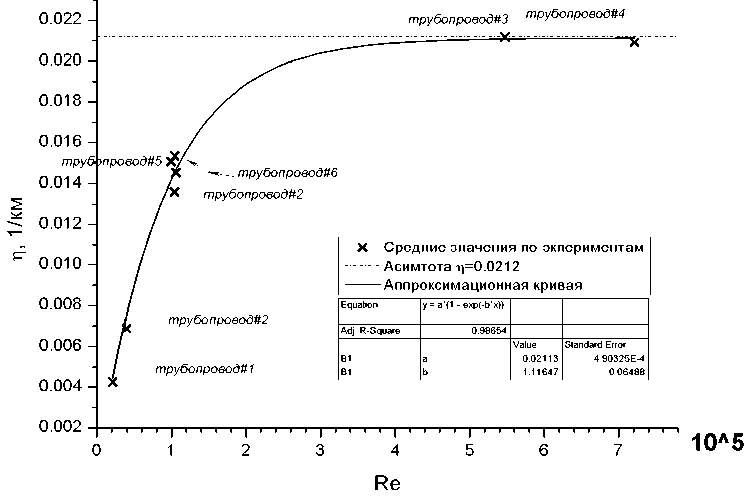
Рис. 4. Зависимость коэффициента затухания от безразмерного числа Рейнольдса

Предложенная эмпирическая зависимость позволяет проводить простую оценку затухания колебательных процессов и одиночных гидроударных волн, распространяющихся вдоль протяженного тракта круглого сечения.

Проведённые на следующем шаге исследования сравнения результатов полученной зависимости с теоретическими расчетами распространения возмущений, полученных вычислительными методами, показали, что наибольшая сходимость эксперимента и теории наблюдается в области малых значений числа Рейнольдса. В области больших значений Re результаты теоретических расчетов расходятся с экспериментом: затухание за счет вязкого трения в эксперименте больше рассчитанных значений.

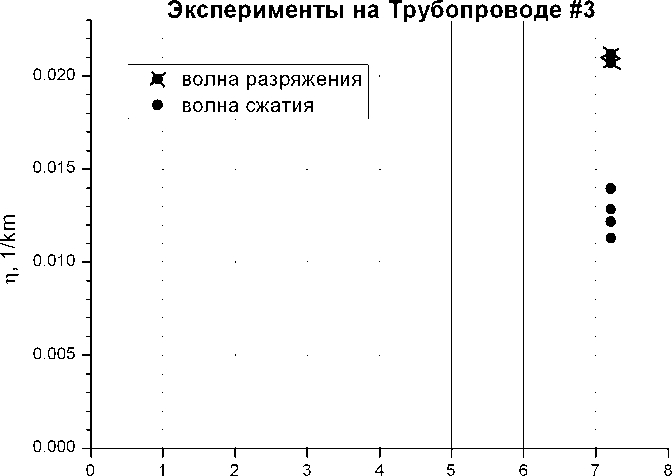
Колебательный процесс состоит из «разгонных» волн сжатия и «тормозящих» волн разрежения. Проведенные серии экспериментов содержали исследования распространения и затуханиях волн обоих типов. Результаты экспериментов (рис. 5) подтвердили теоретические предположения, полученные У. Р. Лийвом в 1983 г. [15]: экспериментальные значения коэффициента затухания волны разрежения значительно меньше коэффициента затухания волны сжатия.

Например, для трубопровода № 3, результаты которого приведены на рис. 5, эта разница составила 0,009 1/км, т. е. затухание волн при торможении потока почти в 2 раза больше чем при разгоне.

На рис. 6, а приведено изображение распределения скорости потока по сечению магистрали в случае отсутствия волны давления. При распространении волны сжатия, т. е. при разгоне потока, профиль течения на фронте волны вытягивается (рис. 6, б ).

В этом случае при и 1 >  и 0 >  0 либо при и 1 <  и 0 <  0 проинтегрированное уравнение (1) в предположении равенства значения X = Х ₀ = const:

При торможении потока (рис. 6, в ) при и 1 >  и ₀ >  0, а также и при и 1 <  и ₀ <  0 , решение того же уравнения принимает вид

Т ^Х0 | ^и 0I . ¹ n₉ =      + — ln

² 2 aD _у x

(      X0 и 0| _х )

^А p 0 1 - e ^{2 aD}у^Х 2 Р ^си 0

M u ol + l_ln 2 aD _у

1 +

^А p 0

2 р си 0

1 — e

x 2 aD _у

Из сравнения полученных формул видно, что n T < n p , т. е. при одинаковых по модулю величинах скорости потока коэффициент затухания при разгоне потока будет больше, чем при торможении. При разгоне потока градиент скорости вблизи стенок трубопровода увеличивается, следовательно, потери на вязкое трение увеличиваются (рис. 6, б ). При торможении потока профиль скорости становится таким, как изображенный на рис. 6, в , градиент скорости уменьшается, а с ним и потери на трение также уменьшаются.

Заключение. В результате проведенных экспериментальных исследований по затуханию ударных гидравлических волн на протяженных магистралях получены эмпирические соотношения показателя затухания в виде функциональной зависимости от критерия Рейнольдса.

Определено, что гармонические составляющие широкополостного спектра импульсного возмущения в турбулентном жидкостном потоке с частотой более 10 Гц при распространении в магистрали быстро затухают и несущественны. Увеличение показателя затухания низкочастотных составляющих спектра возмущения существенным образом определяется вязкостью и гидравлическими потерями и обратно пропорционально связано с волновыми свойствами среды и диаметром трубопровода. Найденные соотношения, описывающие затухание гидроударных волн в турбулентных потоках, используются при проведении инженерных расчетов систем питания жидкостных ракетных двигателей на кафедре ракетных двигателей в Московском авиационном институте.

Re

Рис. 5. Различие коэффициентов затухания гидроударной волны сжатия и разрежения

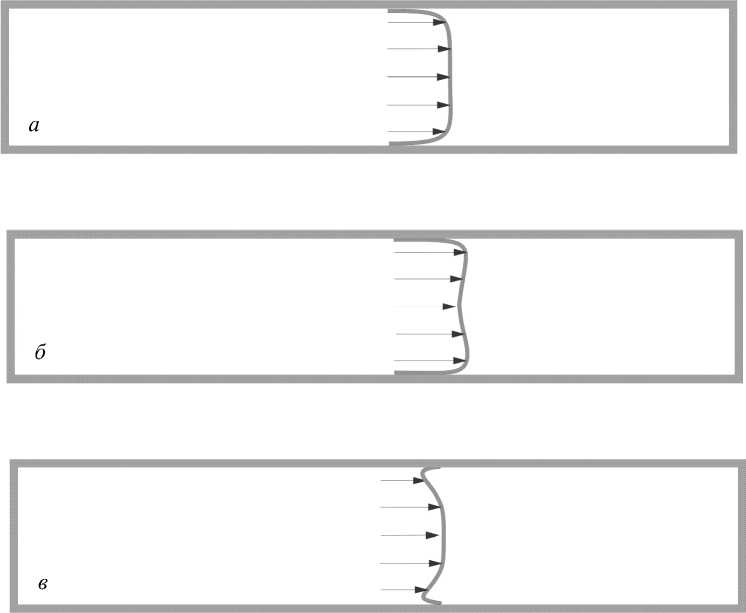
Рис. 6. Изменение профиля скорости на фронте волны

Полученные зависимости будут полезны для оценок воздействия гидроударных волн на агрегаты, арматуру и трубопроводы при проведении приемосдаточных испытаний (КТИ) и других видов испытаний жидкостных ракетных двигателей на предприятиях, занимающихся их разработкой и изготовлением.