Зависимость спина основного состояния активного центра Fe 2S 2 ферредоксина от ориентации лигандов

Автор: Лыхин А.О., Кузубов А.А., Варганов С.А., Сержантова М.В., Елисеева Н.С.

Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau

Рубрика: Математика, механика, информатика

Статья в выпуске: 4 (44), 2012 года.

Бесплатный доступ

В рамках теории функционала плотности рассмотрено строение окисленной формы кластера [2Fe-2S-4(SCH 3)] 2-, являющегося аналогом активного центра белка ферредоксина. Показана возможность неадиабатических спин-запрещенных переходов между конформерами кластера, находящимися в синглетном и триплетном спиновых состояниях. Полученные переходные структуры могут быть использованы при изучении механизма реакций кластера с участием вырожденных спиновых состояний.

Ферредоксин, неадиабатические процессы, теория функционала плотности

Короткий адрес: https://sciup.org/148176913

IDR: 148176913

Текст научной статьи Зависимость спина основного состояния активного центра Fe 2S 2 ферредоксина от ориентации лигандов

Широко используемое в квантовой химии адиабатическое приближение предполагает расчет энергии структуры при фиксированных положениях ядер атомов и нахождении системы в основном электронном состоянии. Однако в ряде случаев разница между основным и возбужденным состоянием может быть достаточно мала, в результате чего становится возможным переход на поверхность потенциальной энергии возбужденного состояния. Изучение таких неадиабатических процессов является одной из наиболее актуальных задач в области динамики химических реакций [1; 2].

Описание спинового состояния системы играет особую роль в элементоорганической и бионеоргани-ческой химии [3]. В частности, давно известно, что изменение спинового состояния напрямую связано с протеканием реакций, в которых участвуют гемопротеины [4]. Все большее значение приобретает контроль спинового состояния в каталитических процессах, например с участием железа [5]. Реализация неадиабатических эффектов в системах с переходными металлами напрямую связана со спин-орбитальным взаимодействиям между электронными состояниями с разными спинами. В этой связи особое внимание уделяется рассмотрению железосодержащих белков, например ферредоксина. В качестве активного центра этого белка чаще всего выступает биядерный кластер [2Fe–2S], который связан с четырьмя цистеиновыми остатками, формирующими близкое к тетраэдрическому окружение для каждого атома Fe. Такая модель активного центра характеризуется заменой цистеиновых остатков на тиометильные группы.

Применение теории функционала плотности в моделировании структуры активного центра ферредоксина показало возможность существования окисленной формы кластера [2Fe–2S–4(SCH3)]2– в виде одной из 17 равновесных конформаций, отличающихся величиной двугранного угла, образуемого атомами Fe– Fe–S–C [6]. Однако кристаллографические данные строения белков свидетельствуют об отклонениях рассчитанных значений углов в газовой фазе от экспериментальных, что, по мнению авторов, связано с аминокислотным окружением активного центра ферредоксина. Вместе с тем геометрические параметры системы оказывают определяющее влияние на спиновое состояние кластера, его нахождение в устойчивом, возбужденном или переходном состоянии. Установление возможности существования системы в вырожденном спиновом состоянии является важнейшим этапом на пути исследования механизма реакций, протекающих по неадиабатическому спин-запре-щенному механизму [7].

На основании квантово-химических расчетов, приведенных в [6], были рассмотрены пять наиболее энергетически выгодных структур окисленной формы кластера [2Fe–2S–4(SCH 3 )] 2– , отличающихся величинами двугранных углов Fe–Fe–S(Cys)–C, где S(Cys) – терминальные атомы серы. Моделирование отобранных конформеров выполнялось в рамках теории функционала плотности в квантово-химическом пакете GAMESS [8]. При расчетах использовался обменно-корреляционный функционал PBE [9] в базисном наборе def2-TZVP [10]. Выбор этого базисного набора был обусловлен высокой точностью приближения, характеризующегося стандартным отклонением в энергии атомизации на атом, равным 0,022 эВ при средней ошибке в длине связи менее 1 пм, и отклонением в величине угла менее 1º.

Оптимизация конформеров проводилась без наложения ограничений по симметрии до достижения стандартного критерия сходимости. Были рассмотрены конформеры в антиферромагнитном состоянии (S = 0) и триплетном спиновом состоянии. Для наиболее энергетически выгодных конформеров также рассчитывались состояния с более высокой мультиплет-ностью.

Геометрические параметры полученных конформеров представлены в табл. 1.

Атомы железа и связанные с ними мостиковые атомы серы S3 и S4 расположены практически в одной плоскости. Выход атома серы из плоскости трех атомов не превышает 4º (рис. 1). Для описания двугранных углов введен фиктивный атом X, такой, что прямая, проходящая через атомы X и Fe2, перпендикулярна прямым Fe1–Fe2 и S3–Fe2. Таким образом, два атома железа и фиктивный атом X вместе образуют плоскость σ, перпендикулярную к плоскости Fe1–Fe2–S3.

Таблица 1

№ конформера	Атом	^φ1	Abs	Атом	^φ2	Abs	^φ3
Синглетное спиновое состояние
A1	S5	23	23	C9	176	4	0,04
	S6	–157	23	C10	–3	3
	S7	23	23	C11	–174	6
	S8	–157	23	C12	3	3
B1	S5	–24	24	C9	176	4	0,2
	S6	158	22	C10	0	0
	S7	22	22	C11	177	3
	S8	–156	24	C12	–2	2
C1	S5	–27	27	C9	154	26	2,1
	S6	142	38	C10	118	62
	S7	21	21	C11	–5	5
	S8	–157	23	C12	–3	3
D1	S5	–2	2	C9	–112	68	0,3
	S6	176	4	C10	19	19
	S7	–5	5	C11	120	60
	S8	177	3	C12	120	60
E1	S5	3	3	C9	112	68	1,0
	S6	–175	5	C10	–18	18
	S7	–3	3	C11	124	56
	S8	176	4	C12	118	62
X1	S5	4	4	C9	117	63	1,7
	S6	–174	6	C10	125	55
	S7	5	5	C11	25	25
	S8	–174	6	C12	30	30
A3	S5	Три 0	плетное спиново 0	е состояние C9	–109	71	3,5
	S6	177	3	C10	23	23
	S7	–11	11	C11	173	7
	S8	165	15	C12	–3	3
B3	S5	5	5	C9	108	72	3,4
	S6	–173	7	C10	–19	19
	S7	17	17	C11	–176	4
	S8	–159	21	C12	4	4
C3	S5	5	5	C9	118	62	1,3
	S6	–174	6	C10	125	55
	S7	18	18	C11	6	6
	S8	–162	18	C12	7	7
D3	S5	–4	4	C9	–116	64	0,7
	S6	175	5	C10	26	26
	S7	–16	16	C11	133	47
	S8	165	15	C12	134	46
E3	S5	3	3	C9	116	64	0,3
	S6	–176	4	C10	103	77
	S7	16	16	C11	135	45
	S8	–165	15	C12	131	49

Окончание табл. 1

№ конформера	Атом	^φ1	Abs	Атом	^φ2	Abs	^φ3
Переходное спиновое состояние
I	S5	5	5	C9	118	62	1,5
	S6	–174	6	C10	125	55
	S7	14	14	C11	12	12
	S8	–166	14	C12	14	14
II	S5	5	5	C9	119	61	1,4
	S6	–173	7	C10	125	55
	S7	15	15	C11	20	20
	S8	–166	14	C12	11	11

Примечание. В таблице приняты следующие обозначения: φ 1 – двугранный угол X–Fe1–Fe2–S(Cys); φ 2 – двугранный угол Fe–Fe–S(Cys)–C; φ 3 – двугранный угол Fe–Fe–S3–S4; Abs – абсолютное значение углов; все величины приведены в градусах.

Таблица 2

Относительные энергии оптимизированных структур

Структура	E , ккал/моль	Атомная спиновая плотность		Спин S Z	S ²
Структура	E , ккал/моль	Fe1	Fe2	Спин S Z	S ²
A1	11,4	–0,367	0,365	0	2,266
A3	5,5	–0,343	0,498	1	4,051
B1	11,0	–0,369	0,360	0	2,207
B3	5,5	–0,347	0,499	1	4,076
C1	1 865,9	–0,721	0,348	0	2,165
C3	3,8	–0,349	0,504	1	4,042
D1	0	–0,504	0,503	0	4,000
D3	9,0	–0,320	0,490	1	4,065
E1	0,1	–0,504	0,503	0	4,001
E3	9,4	–0,324	0,492	1	4,029
X1	0,9	–0,505	0,504	0	4,007

Двугранные углы φ 1 показывают отклонение плоскости Fe1–Fe2–S(Cys) от σ, в свою очередь двугранные углы φ 2 Fe–Fe–S(Cys)–C характеризуют выход углерода из плоскости, формируемой атомами железа и терминальным атомом серы, с которым углерод непосредственно связан. При определении углов φ 2 первый атом железа выбран как наиболее удаленный от атома углерода. В соответствии с нумерацией атомов в соединении к терминальным атомам серы S(Cys) относятся атомы S5 и S6, связанные с Fe1, а также S7 и S8, связанные с Fe2.

Согласно значениям, представленным в табл. 2, наиболее энергетически выгодную конфигурацию в синглетном спиновом состоянии имеют два конформера: D1 и E1, в триплетном состоянии – конформер C3.

В случае конформеров в синглетном состоянии распределение спиновой плотности на атомах железа свидетельствует об антиферромагнитном упорядочении спинов, при котором неспаренные электроны с одинаковыми спинами локализованы на разных атомах Fe. Рассчитанные спиновые плотности для Fe1 и Fe2 равны по абсолютным значениям и противоположны по знаку. Отклонение, наблюдаемое в случае конформера C1, обусловливает его высокую неустойчивость по сравнению с другими структурами.

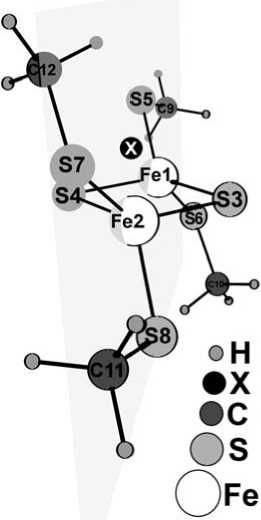
Рис. 1. Строение конформера A1 кластера [2Fe–2S–4(SCH 3 )]^2–

Двугранные углы оптимизированных структур кластера [2Fe–2S–4(SCH3)]2–

Вместе с тем для конформеров в синглетном спиновом состоянии характерны исчезающе малые величины спиновой плотности на мостиковых атомах S – около 1 · 10 –4 электрон/атом, которые возрастают в среднем на два порядка при переходе системы в триплетное состояние. Значительная делокализация спиновой плотности проявляется лишь на мостиковых атомах S, в то время как у терминальных атомов S подобного эффекта не наблюдается. Используя значения квадратов длины вектора спинового момента, можно определить величину суммарного спинового числа, которая для значений S 2 , равных 4 и 2, округленно составит 3/2 и 1. Поскольку заряды атомов железа равны, то в случае S 2 ≈ 2 каждый из электронов локализуется на одном из атомов железа. При этом проекции спина у электронов направлены в противоположные стороны, что дает суммарную проекцию спина, равную 0. В случае S 2 ≈ 4 электронное облако третьего электрона делокализовано между атомами железа и мостиковыми атомами серы.

В соответствии с данными об относительной энергии состояний с различной мультиплетностью для структур фиксированной геометрии C3 и E1, пред-ставлеными на рис. 2, устойчивость состояний иной мультиплетности в сравнении со спиновым состоянием оптимизированной структуры ниже, что свидетельствует о том, что для конформеров C3 и E1 основными являются соответственно триплетное и синглетное спиновые состояния.

Рис. 2. Относительные энергии основных и высокоспиновых состояний конформеров C3 и E1 в сравнении с синглетным спиновым состоянием C3:

темные столбцы – исходный конформер E1; светлые столбцы – исходный конформер C3

Оптимизация геометрии конформеров C3 и E1 в состояниях с различной мультиплетностью приводит к понижению энергии высокоспиновых состояний. Однако в целом они остаются менее энергетически выгодными по сравнению с состояниями С3 и Е1 (рис. 3). При этом в случае оптимизации синглетного состояния структуры C3 получен конформер X1, близкий по энергии к конформерам D1 и E1 и вместе с тем имеющий геометрию, наиболее сходную со структурой C3 (см. табл. 1).

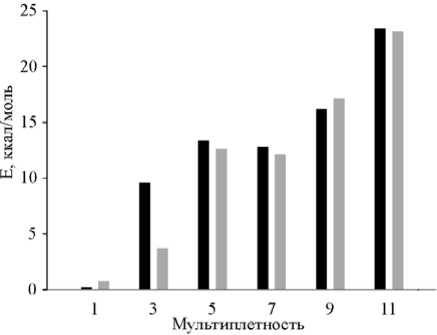
Рис. 3. Относительные энергии оптимизированных структур в сравнении с конформером E1 в синглетном состоянии: темные столбцы – исходный конформер E1; светлые столбцы – исходный конформер C3

Геометрические различия между конформерами C3 (S = 1) и X1 (S = 0) состоят в том, что внешние атомы серы одного из атомов железа выходят из плоскости σ при сохранении положения метильных групп (рис. 4). Таким образом, триплет-синглетный переход с изменением геометрии осуществляется за счет смещения внешних атомов серы, связанных с одним центром. С другой стороны, переходы между конформерами D1 или E1 и C3 зависят от перемещений как атомов S, так и связанных с ними CH 3 -групп.

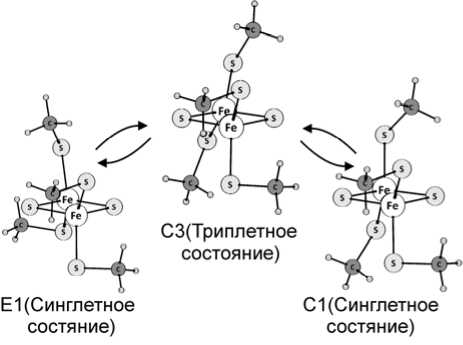
Рис. 4. Основные и высокоспиновые состояния конформеров C3 и E1 [2Fe–2S–4(SCH 3 )] 2– кластера

Переход между конформерами был разделен на 10 промежуточных геометрий. Плавное изменение положений атомов при переходе от одной структуры к другой достигалось путем интерполяции геометрических параметров системы во внутренних координатах [11] (рис. 5, 6).

Перегибы, наблюдаемые в случае C3–E1-перехода (см. рис. 6), связаны с вращением метильных групп. Геометрия, соответствующая пересечению кривых, использовалась в качестве исходной при поиске минимума энергии на пересечении синглетной и триплетной поверхностей потенциальной энергии. Поиск минимума проводился при помощи процедуры MEX пакета GAMESS по стандартным критериям. Полученные переходные состояния близки по геометрическим параметрам и отличаются лишь расположением одной метильной группы.

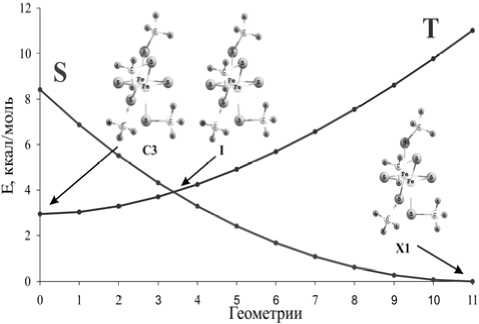
Рис. 5. Относительные энергии структур, характеризующие триплет-синглетный переход I:

геометрия 0 – конформер C3; геометрия 11 – конформер X1

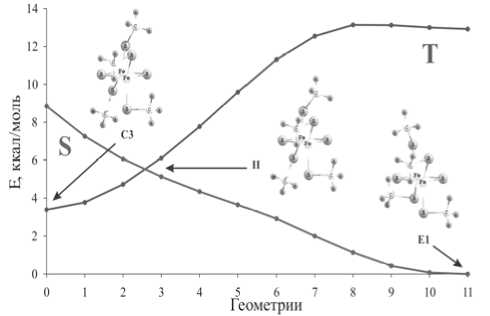
Рис. 6. Относительные энергии структур при триплет-синглетном переходе II:

геометрия 0 – конформер C3; геометрия 11 – конформер E1

В случае перехода II геометрия, отвечающая минимуму энергии на пересечении синглетной и триплетной поверхностей потенциальной энергии, оказалась ниже точки пресечения кривой на рис. 6 на 2,8 ккал/моль.

В результате разница между энергией конформера C3 в триплетном спиновом состоянии и энергией переходного состояния при переходах I и II равна 0,95 и 0,91 ккал/моль соответственно.

Таким образом, незначительные энергетические различия в полученных структурах обусловливают высокую вероятность переходов между устойчивой конформацией С3 в триплетном спиновом состоянии и конформерами E1 и X1 с одновременным понижением мультиплетности системы до синглетного состояния. Подобные переходы являются очень важными в процессах спин-орбитального взаимодействия. При воздействии на геометрические параметры модельного кластера активного центра ферредоксина [2Fe–2S–4(SCH 3 )] 2– , в частности положения лигандов, можно достичь изменения мультиплетности системы. С одной стороны, такие переходы обусловливают возможность существования кластера в различных спиновых состояниях, с другой – открывают широкие возможности по их применению в спин-запрещенном неадиабатическом катализе.

Статья научная