Зависимость температуры стеклования от скорости охлаждения расплава

Природа стеклования жидкостей остается одной из актуальных нерешенных задач физики конденсированного состояния [1, 2]. В отличие от температур фазовых переходов температура стеклования T g зависит от скорости охлаждения расплава q = d T /d t . Проблема взаимосвязи этих величин является важнейшей частью теории стеклообразного состояния. Она важна и для практики, например, для отжига и закалки стекол.

Настоящее сообщение посвящено исследованию зависимости температуры стеклования от скорости охлаждения.

Вывод уравнения

Обратимся к критерию стеклования Бартенева [3]

qτ g = C ,                      (1)

и известной формуле времени релаксации

^T = ^T 0 exp V I F J,

где τ g – время релаксации τ при температуре стеклования T g , С – эмпирическая постоянная, τ 0 – период колебаний молекулы около равновесного положения, Δ F – свободная энергия активации стеклования.

В области перехода жидкость-стекло величина Δ F ( T ) резко возрастает [1, 2], что требует модификации формулы (2). Как правило, свободная энергия активации стеклования Δ F совпадает со свободной энергией активации вязкого течения стеклообразующих расплавов. Принимая это во внимание, для температурной зависимости Δ F ( T ) примем следующее выражение [4]

A F = A F ^ + kT exp

^{- E} I- 1 kT J

которое справедливо в широком интервале температур. Первое слагаемое Δ F ∞ – потенциал перескока атома (кинетической единицы) в новое положение – представляет собой высокотемпературный предел свободной энергии активации Δ F ∞ = Δ F ( T →∞). Во второе слагаемое – потенциал локального конфигурационного изменения структуры Δ F s ( T ) – входит энергия делокализации атома Δ ε e . Процессу «делокализация атома» в неорганических стеклах и их расплавах соответствует некоторое критическое смещение мостикового атома (типа атома кислорода в мостике Si-O-Si), связанное с локальной низкоактивационной деформацией сетки валентных связей [4-6]. У силикатных стекол величина Δ ε e составляет около Δ ε e ≈ 20 кДж/моль [5].

При низких температурах, в области стеклования, в выражении (3) можно пренебречь единицей в квадратных скобках и первым слагаемым Δ F ∞ в сравнении с экспоненциальной зависимостью второго слагаемого, что значительно упрощает зависимость (3)

A F = kT exp I I (4) V kT J .

Принимая во внимание данное равенство, уравнение времени релаксации (2) при температуре стеклования T = T g можно записать в виде “двойной экспоненты”

T g = T 0 exp

exp

1 A Ee —

V g g

Такого рода зависимость для молекулярно-кинетических процессов в стеклообразующих жидкостях в области стеклования предлагалась рядом исследователей в виде эмпирических и полуэмпирических соотношений (например, [7, 8]).

Подставив в равенство (1) время релаксации τ g из формулы (5), после некоторых преобразований получаем следующее уравнение для зависимости температуры стеклования от скорости охлаждения

1                    1 1 inq I

— = ti i + b in I 1-- — I

T g     ^{1    1} V b 2 J ,

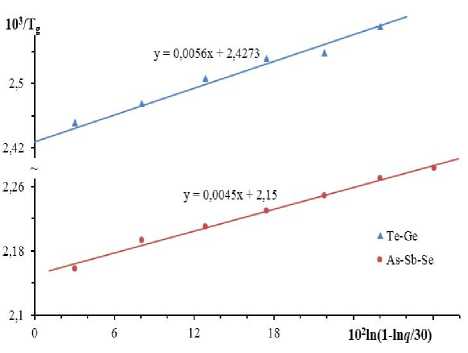
Рис. 1. Зависимость температуры стеклования от скорости охлаждения для стекол As-Sb-Se и Te-Ge в координатах уравнения (6): 1/ T g – ln[1 – (ln q /30)].

Содержание As/Sb/Se, мол.%: 32.91/7.64/59.45 и Te/Ge, мол.%: 90.87/9.13. Параметры уравнения (6) для стекла As-Sb-Se: a 1 = 2,1·10^-3 K ^-1, b 1 = 4,5·10^-3 K ^-1; для стекла Te-Ge: a 1 = 2,4·10^-3 K ^-1, b 1 = 5,6·10^-3 K ^-1. Использованы данные [11].

где b 1 = k /∆ ε e ; b 2 = ln ( C / τ 0 ); a 1 = b 1 ln b 2 .

Сравнение с экспериментом и обсуждение результатов

Температура стеклования чаще всего измеряется в режиме нагревания стекла в процессе его размягчения, поскольку определение Tg в режиме охлаждения стеклообразующего расплава труднее реализовать экспериментально. Будем полагать, что зависимость температуры стеклования от скорости нагревания примерно такая же, как и зависимость Tg от скорости охлаждения. В обоих случаях будем пользоваться одним и тем же обозначением q.

Полагая τ 0 ≈ 10^-12 с и С ≈ 10 К [2, 9, 10], приходим к приближенной оценке параметра b 2

b 2 = ln(C/τ o ) ≈ const ≈ 30

Здесь выражение под логарифмом ( C / τ 0 ) имеет размерность ( К / с ) – градус Кельвина, деленный на секунду. В уравнении (6) скорость охлаждения q имеет такую же размерность: ln ( q , К / с ).

С целью проверки полученного соотношения (6) мы построили графики в координатах ¹ - J i-lnq |

T g V 30 )

для различных аморфных веществ.

Экспериментальные данные [9, 11] в указанных координатах в соответствии с уравнением (6) ложатся на прямые (рис. 1, 2).

При скоростях охлаждения или нагревания lnq << b2 логарифм в правой части равенства (6) можно разложить в ряд и ограничиться его первым членом ln

1 -

k

lnq 1

b 2 ;

ln q b ₂

Тогда соотношение (6) переходит в известное уравнение Бартенева [2, 3]

— = ai - a2 ln q , a2 =—   .(7)

Tg

Следовательно, уравнение Бартенева, которое выводится при допущении Δ F = const [3], справедливо при не очень больших скоростях охлаждения: ln q << 30. В самом деле, при сравнительно высоких скоростях охлаждения для ряда стекол, например, у стеклообразного борного ангидрида и свинцовосиликатных стекол, наблюдается отклонение от этого уравнения (7) (рис. 2). Важно отметить тот факт, что у указанных стекол нет отклонений от эксперимента в координатах, соответствующих полученному соотношению (6) (рис. 3).

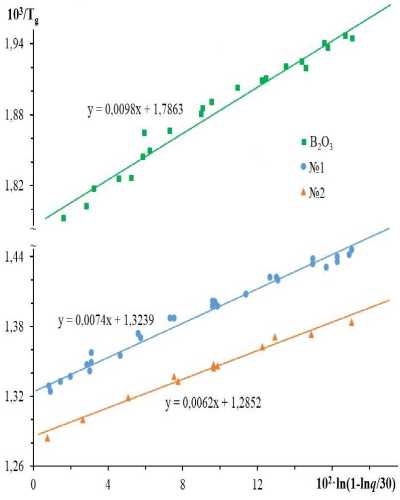
Рис. 2. Зависимость температуры стеклования от скорости нагревания для свинцово-силикатных стекол №1 и №2 и борного ангидрида B 2 O 3 в координатах 1/ T_g – ln(1–ln q /30). Использованы данные [2, 9]. Содержание PbO в стеклах PbO - SiO 2 : №1 – 30 мол.%, №2 – 52 мол.%. Параметры уравнения (6) для стекла №1: a 1 = 1,3·10^-3 K ^-1, b 1 = 7,4·10^-3 K ^-1; для стекла №2: a 1 = 1,2·10^-3 K ^-1, b 1 = 6,2·10^-3 K ^-1 и для B 2 O 3 : a 1 = 1,7·10^-3 K ^-1, b 1 = 9,8·10^-3 K ^-1.

103/T„ K"1

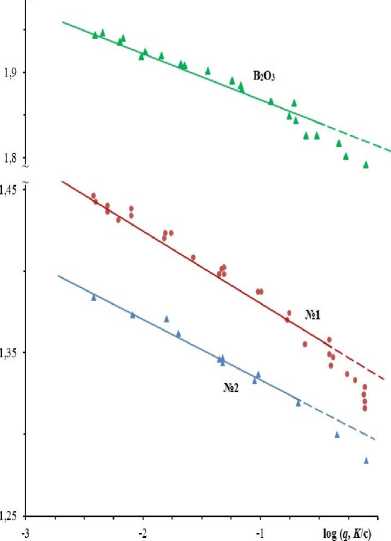
Рис. 3. Зависимость 1/ T g от log q для стеклообразного борного ангидрида B 2 O 3 и для свинцовосиликатных стекол №1 и №2 [2, 9].

Таким образом, предлагаемое нами уравнение (6) находится в удовлетворительном согласии с опытными данными в более широком диапазоне скоростей охлаждения (или нагревания), чем уравнение Бартенева (7). Остановимся кратко на физическом смысле параметров уравнений (6) и (7).

Поскольку параметр b2 ≈ 30 является константой, величина а1 пропорциональна b1 = R/Δεe a 1 = b1 Inb2 « 3.4b1 « 3.4, — |.                                (8)

(^{A E} e J

Отсюда следует, что в обобщенное уравнение (6) входит фактически один параметр, а именно энергия делокализации атома Δ ε e ,

1 ₌ _R_

^Tg   ^{A £} e

, , In q )

• 3. 4 - In I 1---- I

2 . 3 b i . 2 . 3, - R -1 .0 . 08,     | .

(    30 J где R – газовая постоянная. То же самое можно сказать и относительно уравнения Бартенева (7)

1 R

— = а_х - a 2 Igq = -—[ 3 . 4 - 0 . 08 Igq ] ,

Tg               ^Ee поскольку параметр а2 в уравнении (7) оказывается также пропорциональным b1

a 2 =

b ₂     30 (A E e J (A E e J

Таким образом, зависимость Tg = Tg(q) определяется энергией Δεe. Этот результат находится в согласии с представлением о том, что в области стеклования замораживается процесс делокализации активного атома – его смещение из равновесного положения (переход частицы из основного состояния в возбужденное) [5, 6, 10, 12].

Под делокализацией атома в неорганических стеклах и их расплавах подразумевается смещение мостикового атома (типа атома кислорода в мостике Si-O–Si), связанное с локальной низкоактивационной деформацией сетки валентных связей [6].

Бартеневым и Лукьяновым [5, 6] на основе опытных данных а 1 и а 2 было установлено, что отношение этих параметров является практически универсальной величиной у канифоли, эбонита, борного ангидрида, органических аморфных полимеров и силикатных стекол:

2^ . const . 0 . 020 - 0 . 030. a ₁

Данный результат получает определенную интерпретацию в рамках модели делокализованных атомов. В самом деле, как видно из соотношений

• (8)    и (9), отношение а 2 / а 1 оказывается постоянным

a ₂ = 0 . 08 R As e a 1 3 . 4 R As e

. const . 0 . 023,

что по порядку величины вписывается в интервал экспериментальных данных этого отношения (12).

Заключение

Вывод уравнения Бартенева (7) с учетом температурной зависимости энергии активации процесса стеклования показывает, что это уравнение справедливо при не очень больших скоростях охлаждения (нагревания) стеклообразующих расплавов: lnq << 30. Полученное обобщенное уравнение для зависимости температуры стеклования от скорости охлаждения (6) описывает эту зависимость в более широком диапазоне скорости охлаждения/нагревания, чем уравнение Бартенева (7).

Установлено, что параметры уравнений (6) и (7) для зависимости T g ( q ) являются однозначными функциями энергии делокализации атома Δ ε e , что согласуется с представлением о том, что в области стеклования замораживается процесс делокализации атома – его смещение из равновесного положения.

В рамках модели делокализованных атомов получает определенную интерпретацию постоянство отношения параметров уравнения Бартенева ( а 2 / а 1 ) ≈ const .