Зависимость зоны разрушения массива вокруг горной выработки от предела прочности породы

Исследованию геомеханических явлений и процессов в массивах горных пород, проявляющихся при добыче полезных, ископаемых посвящено большое количество научных трудов [1-7]. Во многих из них рассматриваются вопросы оптимизации процесса добычи полезных ископаемых. Среди них особое место занимает задача зональной дезинтеграции горных пород вокруг глубоких подземных выработок [8 - 13]. К примеру разработан механизм зональной дезинтеграции при ударном разрушении вмещающего массива горных пород вокруг глубокой камеры [14]. Получено общее решение уравнения движения фронта волны с помощью преобразования Лапласа. Проведен анализ определяющего уравнения удара и критерия зонального разрушения вмещающего массива горной породы на основе скорости частиц, дифференциального давления на фронте волны и сохранения количества движения.

В работе [15] построена модель механизма зональной дезинтеграции изотропных массивов горных пород вокруг глубокого сферического туннеля в условиях динамической разгрузки и всестороннего сжатия. Показано влияние различных параметров модели изотропных глубоких горных массивов на явление зональной дезинтеграции вмещающего массива горных пород вокруг глубоких сферических туннелей и распределение поля общих упругих напряжений.

В работе [16] исследован механизм зональной дезинтеграции вмещающего массива горных пород вокруг глубоких туннелей, проведен анализ данных, полученных в ходе лабораторных исследований на гипсовых моделях при статикодинамическом комбинированном нагружении образца. Установлена зависимость характера разрушения нагруженного образца при периодической динамической нагрузке от различных статически напряженных состояний. Зафиксировано,

МИСиС

что увеличение диаметра туннеля способствует появлению слоистого нарушения вмещающего массива горных пород вокруг глубокого туннеля при фиксированном статико-динамическом нагружении. Несмотря на это вопрос разработки моделей, адекватно описывающих процесс зональной дезинтеграции массива горных пород и исследования ее механизма, остается открытым.

В настоящей работе проведено уточнение аналитической зависимости расположения середины первой зоны разрушения, измеряемой в относительных к радиусу выработок единицах, от предела прочности породы на одноосное сжатие. Построена альтернативная нелинейная модель, для которой проведен сравнительный анализ с ранее полученными результатами и экспериментальными данными. Показаны её значимость и сходимость с натурными данными.

Модель зональной дезинтеграции горных пород вокруг подземной выработки

Обратимся к задаче о распределении поля напряжений вокруг выработки круглого сечения, которая рассматривается как плоская и стационарная, в условиях несжимаемости и гидростатичности нагружения на бесконечности:

∂σ 1

^rr +   ( σ _rr -σ_φφ ) = 0,

∂rr определено бигармоническое уравнение для функции дефектности

∆² R -γ² R =0

и граничные условия

R    =0, ∂R r=r0        ∂r

= 0, Lim R(r) = 0, r=r0      r→∞ где σrr - нормальное радиальное напряжение; σϕϕ - нормальное тангенциальное напряжение, ∆ - оператор Лапласа, γ - параметр периодичности модели [17].

Решение для расстояния от центра выработки до точки массива определено в виде равенства где J 0 , N 0 , K 0 – функции Бесселя, Неймана и Макдональда нулевого порядка.

Вопрос качественного и точного определения параметров построенной модели имеет численное решение в общем виде [18] и аналитическое для некоторых месторождений [19]. Однако по мере увеличения данных о новых месторождениях полученные аналитические оценки требуют уточнения.

Оценка статистической значимости уравнений регрессий

В работе [19] по натурным данным различных месторождений (табл. 1) получена линейная зависимость вида r∗ =0,008σ +0, 757, (1) где r ∗ – положение середины первой зоны разрушения, измеряемой в относительных к радиусу выработок единицах; σ – предел прочности породы на одноосное сжатие.

Таблица 1

Положение первой зоны разрушения по данным экспериментов

σ, МПа	Экспериментальное значение r	Теоретическое ∗ значение r
8,000	0,80	0,821
25,00	1,00	0,957
50,00	1,13	1,157
100,0	1,50	1,557
150,0	2,00	1,957

Несмотря на высокую корреляционную связь полученного уравнения (1), более детальный статистический анализ показал, что зависимость положения середины первой зоны разрушения от предела прочности породы возможно представить в нелинейном виде:

r ^∗ =0,8133exp(0,0061σ).     (2)

А именно коэффициент детерминации R ² линейного уравнения регрессии составляет 99,12 %, нелинейного уравнения – 99,18 %:

R ² = 1 - ^ост ,                   (3)

S r ²

R ( r ) = aJ ₀(V γ r ) + bN ₀(V γ r ) + cK ₀(V γ r ),

МИСиС

где S r - общая дисперсия признака r * ; S ост — остаточная дисперсия соответствующего уравнения регрессии [20].

Статистическая значимость параметров уравнений регрессии и коэффициентов детерминации подтверждается t -критерием Стьюдента (табл. 2) при 5 %-ном уровне значимости и выполнении необходимого условия:

tрасч > tтаб , где

t ^{( b} ) расч

о ^{2   ;}

t ⁽ R ) расч

R^n - 2

V1 - R R ’

tтаб - табличное значение при заданном уровне значимости. Здесь n - число данных; Г - среднее арифметическое предела прочности породы; а, b - параметры линейного и линеаризованного уравнения соответственно [20].

S’ ост

Таблица 2

Статистическая значимость параметров уравнений егрессии Вид уравнения t ( а )расч t (b )расч t ( R )расч tтаб * r = а о + b 18,38 20,02 18,43 3,182 r* = b exp(а о) 13,73 5,51 19,06 a VS(o-o)2

t ⁽ a ) расч

Статистическая значимость в целом полученных уравнений регрессии подтверждена F -критерием Фишера (табл. 3), при 1 %-ном уровне значимости и выполнении необходимого условия:

F расч таб , где ^,асч = R2(n - 2)/(1 - R2) ; Fтаб - табличное значение при заданном уровне значимости [20].

Таблица 3

Статистическая значимость уравнений регрессии

Вид уравнения	F расч	F -F таб
* r = а о+ b	337,84	34,12
r* = b exp( а о)	381,05

Необходимо отметить, что F расч линейной регрессии меньше Fрасч нелинейной, следовательно, в парном сравнении по F-критерию Фишера последнее более значимо.

Помимо этого по, известным значениям о построены доверительные зоны линии регрессии и доверительные интервалы для обеих линий регрессии (рис. 1). Парный сравнительный анализ показал, что как в случае с доверительной зоной линии регрессии, так и в случае доверительных интервалов, их протяженность в нелинейной модели меньше на 1,035 %.

МИСиС

a )

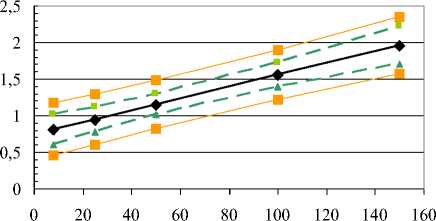
б )

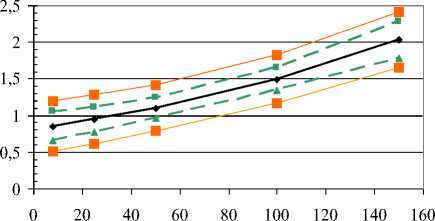
Рис. 1. Модель линейной зависимости ( а ); модель нелинейной зависимости ( б)

Определение относительной ошибки прогноза как отношение стандартной ошибки уравнения регрессии к среднему значению её зависимой переменной подтверждает преимущество нелинейной модели [20]. В нелинейном случае ошибка составила 3,85 % по сравнению с 3,99 % в линейной зависимости.

Заключение

Таким образом, в прогнозировании и аналитическом определении положения середины первой зоны разрушения в случаях, когда диапазон предела прочности породы на одноосное сжатие находится в интервале от 8 до 150 МПа, целесообразнее использовать нелинейную модель.

В общем случае появление новых натурных данных из разработанных месторождений позволит более точно разрешить вопрос статистической значимости обеих моделей. Однако на данном этапе, в условиях предельно ограниченной выборки, можно с большой долей вероятности говорить о наличии нелинейной связи.

Благодарность

Работа выполнена при поддержке Российского научного фонда № 14-11-00079.

• 1.    Chen X.G. ， Zhang Q.Y. Mechanism analysis of phenomenon of zonal disintegration in deep tunnel model test under high geostress // Rock and Soil Mechanics. – 2011. – Vol.32. – № 1. – P. 84–90.

• 2.    Qian Q.H., Zhou X.P. Non-Euclidean continuum model of the zonal disintegration of surrounding rocks around a deep circular tunnel in a non-hydrostatic pressure state // Journal of

  Mining Science. – 2011. – № 47(1). – P. 37– 46. doi:10.1134/S1062739147010059

• 3.    Qian Q.H., Zhou X.P. Quantitative analysis of rockburst for surrounding rocks and zonal disintegration mechanism in deep tunnels // Journal of Rock Mechanics and Geotechnical Engineering. – 2011. – № 3(1). – P. 1–9. doi:10.3724/SP.J.1235.2011.00001

• 4.    Tan Y.L., Ning J.G., Li H.T. In situ explorations on zonal disintegration of roof strata in deep coal mines // International Journal of Rock Mechanics and Mining Sciences. – 2012. Vol. 49. – № 1. – P.113–124.

• 5.    Zhou X.P., Shou Y.D. Excavation induced zonal disintegration of the surrounding rock around a deep circular tunnel considering unloading effect // International Journal of Rock Mechanics & Mining Sciences. – 2013. – № 64. – Pp. 246–257.

• 6.    Wang X., Pan Y., Zhang Z.. A Spatial Strain Localization Mechanism of Zonal Disintegration through Numerical Simulation // Journal of Mining Science. – 2013. – Vol. 49. – № 3. – P. 357–367

• 7.    Zhou X.P., Song H.F., Qian Q.H. The effects of three-dimensional penny-shaped cracks of zonal disintegration of the surrounding rock masses around a deep circular tunnel // Acta Mechanica Solida Sinica. – 2015. – Vol. 28. – № 6. – P.722-734. doi:10.1016/S0894-9166(16)30012-X

• 8.    Одинцев В.Н. Отрывное разрушение массива скальных горных пород. – М.: ИПКОН РАН, 1996. – 166 с.

• 9.    Макаров П.В. Об иерархической природе деформации и разрушения твердых тел и сред // Физ. мезомех. – 2004. – Т. 7. – № 4. – С. 25-34.

• 10.    Гузев М.А., Макаров В.В. Деформирование и разрушение сильно сжатых горных пород вокруг выработок. – Владивосток : Даль-наука, 2007. – 232 с.

• 11.    Зональная дезинтеграция горных пород и устойчивость подземных выработок/ [В.Н.

• 12.    Ксендзенко Л.С., Макаров В.В., Опана-сюк Н.А., Голосов А.М. Закономерности деформирования и разрушения сильно сжатых горных пород и массивов: монография / Инженерная школа ДВФУ. – Владивосток: Дальневост. федер. ун-т, 2014. – 192 с.

• 13.    Лосев А.С. Статистическая оценка параметра периодичности модели зональной дезинтеграции горных пород // // Бюллетень науки и практики. – 2017. – №7 (20). – С. 78-82.

• 14.    Chen J.G., Zhou T.T., Zhang Y.X. Shock failure mechanism of zonal disintegration within surrounding rock in deep chamber // Rock and Soil Mechanics. – 2011. – № 32(9). – P. 26292634.

• 15.    Gu X.B., Bi J., Xu M. Zonal disintegration mechanism of isotropic rock masses around a deep spherical tunnel // J. Cent. South Univ. – 2015. – № 22. – P. 4074-4082.

• 16.    Zuo Y.J., Ma C.D., Zhu W.C., Li S.C., Gong F.Q., Chen C.C. Model test study of mechanism of layered fracture within surround-

  ing rock of tunnels in deep stratum tunneling under dynamic disturbance // Rock and Soil Mechanics. – 2011. – Vol.32. – № 10. – Pp. 2929 - 2938.

• 17.    Гузев М.А., Парошин А.А. Неевклидова модель зональной дезинтеграции горных пород вокруг подземной выработки // Прикладная механика и техническая физика. – 2001. – Том 42. – №1. – С. 147–156.

• 18.    Ксендзенко Л.С., Лосев А.С. Оптимизация вычисления параметра периодичности модели зонального разрушения массива горных пород // Горные науки и технологии. – 2016. – № 2. – С. 43-49. doi:10.17073/2500-0632-2016-2-43-49

• 19.    Ксендзенко Л.С. Разработка метода определения параметров зональной структуры разрушения сильно сжатого массива вокруг подземных выработок // Вестник Дальневосточного государственного технического университета. – 2011. – № 3/4(8/9). – С.144–166.

• 20.    Кузнецова О.С., Тиндова М.Г. Эконометрика: учеб. пособие. – Саратов: CСЭИ РЭУ им. Г.В. Плеханова, 2015. – 108 с.

  “Gornye nauki i	tehnologii”/ “Mining science and technology”, 2017, No. 2, pp. 43-47
  Title:	Dependence of the Zone Destruction the Massive around Mine Workings from the Limit Strength of the Breed
  Author 1	Name&Surname : Alexandr S. Losev Company : Federal State Institution of Science Institute for Applied Mathematics, Far-Eastern Branch of the Russian Academy of Sciences Address: 7 Radio st., Vladivostok, Russian Federation Work Position: Associate Professor, Senior Researcher Scientific Degree : Cand. Sci. (Phys.-Math.) Contacts : A.S.Losev@yandex.ru
  DOI	10.17073/2500-0632-2017-2-43-47
  Abstract:	In the real work the problem of zonal disintegration of rocks around deep underground workings is considered. The review of new works of foreign scientists in the field is provided. Their main results are reflected, the used methods and approaches are described. In the work the task about distribution of the field of tension around development of round section, in the conditions of an incompressibility and hydrostatic character of a loading on infinity is considered. To be carried out the statistical assessment of a significance of earlier received analytical dependence, the linear look, an arrangement of the middle of the feed zone of destruction measured in the relative to the radius of developments units from ultimate strength of breed on an axial compression. The alternate is constructed statistically the reasonable model of a non-linear look describing dependence of the considered parameters. The comparative analysis with earlier obtained results and the experimental datas is carried out. Statistical significance of non-linear dependence of an arrangement of the feed zone of destruction, from ultimate strength of breed, its convergence with natural data and advantage before dependence of the linear look is shown.

doi:10.1016/ j.ijrmms.2013.08.010