Зависимости скорости распространения включенного состояния от геометрических параметров тиристора

Введение. Линейная скорость распространения включенного состояния (РВС) v в тиристорной структуре (ТС) зависит от величин ее электрофизических параметров, геометрических параметров (параметров встроенных шунтов) и плотности тока в открытом состоянии j и является переменной величиной во времени и пространстве. Зависимость скорости РВС от плотности тока v ( Jt ) обычно описывают степенной или, соответственно, логарифмической эмпирическими зависимостями [1–4]:

^v(j T ) = Ah¹ /n ,                               (1)

vfr) = С1 lnjT + C2,                            (2)

где A , n , С и C 2 — константы. Эти зависимости получены экспериментальным путем на конкретных опытных образцах ТС. Причем из всех этих констант приводятся значения только константы n и в очень широком диапазоне: от 2 до 6 [1; 3].

Что касается влияния геометрических параметров – диаметра шунтов и плотности шунтировки на скорость РВС, то в литературе подобных эмпирических зависимостей не приводится. Поэтому целью работы было определение данных зависимостей.

Разработка модели тиристора и моделирование. В работе для решения данной задачи использовалось компьютерное моделирование процессов в ТС на основе пакета программ приборно-технологического моделирования Synopsys TCAD.

Современные тиристоры имеют разветвленный управляющий электрод (УЭ) достаточно сложной конструкции. Промоделировать процессы, протекающие в таком тиристоре, не представляется возможным. Однако из топологии ТС можно выделить трехмерную элементарную ячейку, с помощью которой можно исследовать процесс РВС. Принцип выделения такой ячейки из топологии ТС для моделирования описан в [5; 6].

В качестве объекта моделирования была использована ТС типичного быстродействующего импульсного силового тиристора, рассчитанного на величину повторяющегося напряжения в закрытом состоянии U DM = 2 000 В. При этом задавались следующие электрофизические и геометрические параметры ТС: удельное сопротивление n- базы ρ n = 80 Ом ⋅ см; толщина n- базы W n = 280 мкм; время жизни дырок в n- базе τ р = 4 мкс; диаметр шунтов D ш = 200 мкм; расстояние между шунтами L ш-ш = 800 мкм.

Разработанная модель учитывает эффекты высокого уровня инжекции (электроннодырочное рассеяние и Оже-рекомбинацию), влияние концентрации легирующей примеси на электрофизические параметры полупроводниковой структуры (подвижность, время жизни неравновесных носителей заряда, собственную концентрацию свободных носителей заряда) и эффекты, связанные с неодномерным по объему тепловым разогревом структуры под действием протекающих токов. Подробное описание этих эффектов приведено в [7].

Моделировались процессы в ТС при включении по цепи управления в резистивноиндуктивной силовой цепи, питаемой от источника постоянного напряжения U 0 = 2000 В. Индуктивность силовой цепи выбиралась такой, чтобы время нарастания тока в открытом состоянии было порядка 10 мкс. Амплитуда тока в открытом состоянии регулировалась величиной активного резистора силовой цепи.

В результате моделирования были получены распределения плотности тока по моделируемой элементарной ячейке ТС в заданные моменты времени относительно подачи импульса управления на УЭ, на основании которых были определены зависимости v ( jT ) при различных значениях геометрических параметров ТС.

На рисунке 1 показаны графики зависимости v ( j ) при изменении диаметра шунтов

Эш, на рисунке 2 показаны графики зависимости v(Jt) при изменении расстояния между шунтами Ьш-ш.

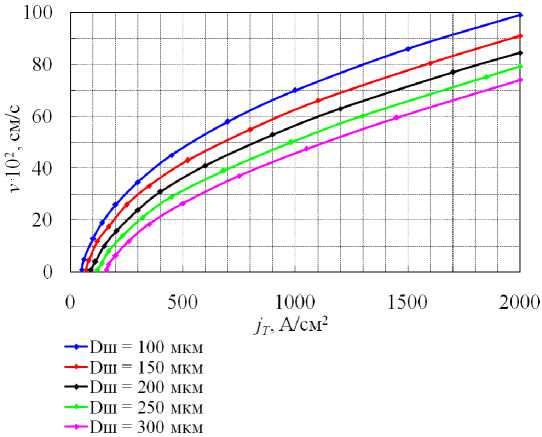
Рис. 1. Графики зависимостей v ( Jt ) для различных значений Э ш .

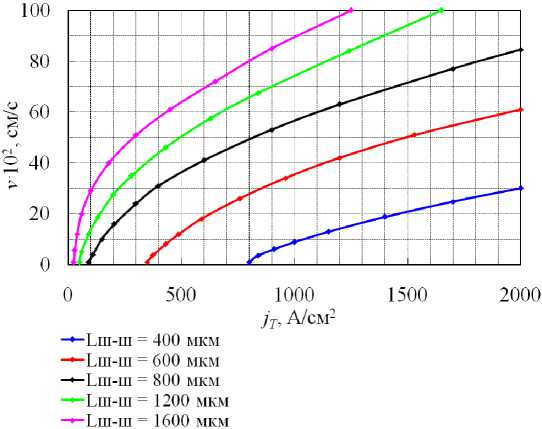
Рис. 2. Графики зависимостей v ( Jt ) для различных значений Ь ш-ш.

Далее были построены графики зависимости скорости РВС от диаметра шунтов v( D ) и расстояния между шунтами v(L ) при значениях плотности тока 200 А/см² и 1 000 А/см². На рисунке 3 показаны графики зависимости скорости РВС от диаметра шунтов.

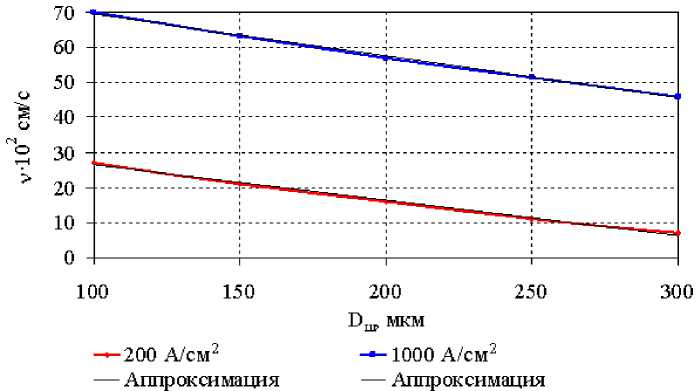
Рис. 3. Графики зависимости скорости РВС от диаметра шунтов при значениях плотности тока 200

А/см2 и 1 000 А/см2.

Как видно из рисунка, эти графики достаточно хорошо аппроксимируются линейной зависимостью v(D_m) = Q D_m + C 2 со следующими значениями коэффициентов:

С 1 = –10 с^–1, С 2 = 3 640 см/с при j = 200 А/см²;

С 1 = –12 с^–1, С 2 = 8 152 см/с при j = 1 000 А/см².

На рисунке 4 показаны графики зависимости скорости РВС от расстояния между шунтами.

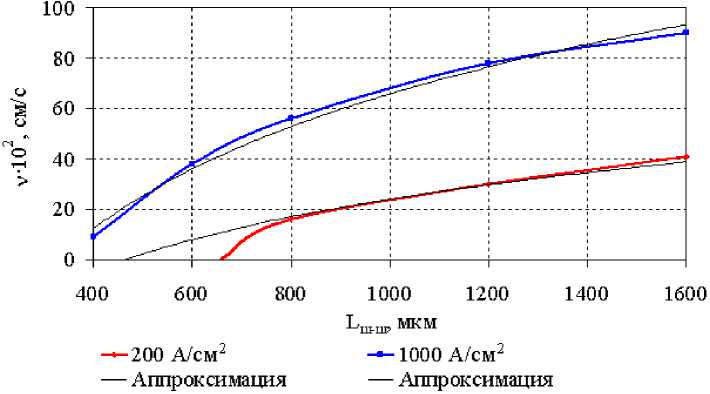
Рис. 4. Графики зависимости скорости РВС от расстояния между шунтами при значениях плотности тока 200 А/см2 и 1 000 А/см2.

Эти графики лучше всего аппроксимируются логарифмической зависимостью v(L_lu__lu) = С lnL_w__ш + C ₂ со следующими значениями коэффициентов:

С 1 = 3 141 см/(с • ln (см)), С 2 = -19 294 см/с при j_T = 200 А/см²;

С 1 = 5 845 см/(с • ln (см)), С 2 = -3 3 793 см/с при j_T = 1 000 А/см².

Однако, как видно из сравнения рисунков 3 и 4, погрешность аппроксимации для графиков зависимости скорости РВС от расстояния между шунтами гораздо больше, чем погрешность аппроксимации для графиков зависимости скорости РВС от диаметра шунтов, особенно для значения j = 200 А/см² в диапазоне значений диаметра шунтов от 400 до 800 мкм.