Здоровье и образование детей в российских регионах: от кластеризации к имитационному моделированию

Актуальность

В современных условиях дети становятся социальным капиталом общества. Они важны для воспроизводства рабочей силы, передачи социально-культурных ценностей и норм, а значит, поддержания стабильности, сохранения государственности, дальнейшего социально-экономического и культурного развития страны.

Отечественными исследователями предпринимались попытки изучения образования детей [6, 7, 9], здоровья детей [1, 2, 5] в региональном разрезе. Для комплексного описания региональных особенностей учеными часто используется понятие ИРЧП (индекс развития человеческого потенциала), под которым понимается комбинированный показатель, характеризующий развитие человека в странах и регионах мира для сравнения и измерения уровня жизни, грамотности, образованности и долголетия [3]. В 2015 г. 6 субъектов Российской Федерации имели очень высокий ИРЧП (г. Москва (0,9018), г. Санкт-Петербург (0,8477), Ненецкий автономный округ (0,8337), Ямало-Ненецкий автономный округ (0,8061), Тюменская область (0,8047) и Ханты-Мансийский автономный округ – Югра (0,8011)) [10].

Объект и методы

Объектом нашего исследования выступают региональные различия социального потенциала детства, а целью – построение имитационной модели социального потенциала детства в российских регионах.

Социальный потенциал детства в российских регионах определяется нами следующим образом: «совокупность ресурсов, резервов и возможностей детей как особой социально-демографической общности, проживающей на территории какого-либо региона (субъекта Российской Федерации), реализующихся под воздействием внешних и внутренних факторов, направленных на достижение качественного состояния детства в области здоровья, образования и духовно-нравственного развития, формирование набора стартовых ресурсов, необходимых для выхода во взрослую жизнь» [12]. Однако анализ статистических данных заставил нас отказаться от третьей целевой после образования и здоровья детей составляющей качественного состояния детства – его духовно-нравственного развития – по причине отсутствия соответствующих показателей в российской статистике.

В итоге целевыми ориентирами развития социального потенциала детства в российских регионах определены – здоровье и образование детей, фиксируемые через следующие целевые факторы: Y1 – средний балл ЕГЭ по русскому языку, балл; Y2 – доля выпускников без аттестата (численность без аттестата к общей численности), %; Y3 – отношение детей, не обучающихся в образовательных организациях, к численности населения младше трудоспособного возраста, %; Y4 – доля детей, больных туберкулезом, %; Y5 – доля детей, больных злокачественными новообразованиями, %; Y6 – число детей-инвалидов (0–17 лет), состоящих под наблюдением в амбулаторно-поликлинических учреждениях, оказывающих медицинскую помощь детям, чел.; Y7 – отношение численности детей I–II групп здоровья к численности населения младше трудоспособного возраста, %; Y8 – число умерших в возрасте до пяти лет на 1000 родившихся живыми, чел.; Y9 – смертность детей от внешних причин смерти в возрасте 0–17 лет на 100 000 человек соответствующего возраста, чел.

Данные, собранные на предыдущих этапах работы [11–13], были взяты за основу для проведения корреляционного анализа. В итоге был сформирован набор из 38 управляющих факторов, включающий группы инфраструктурных (образование, здравоохранение, культура и спорт, транспорт), социально-экономических, территориально-поселенческих, демографических и экологических факторов (табл. 1).

Для расчетов использовались статистические данные, представленные в сборнике «Регионы России. Социально-экономические показатели», сайта Единой межведомственной информационно-статистической системы (ЕМИСС), органов исполнительной власти субъектов Российской Федерации и др. [4, 8]. Данные взяты за 2015–2016 учебный год. Выборочная совокупность охватывает 75 регионов. По разным причинам (чаще всего из-за отсутствия данных) в выборку не были включены Архангельская, Сахалинская, Тюменская области, Ненецкий и Чукотский автономные округа, Республики Алтай, Дагестан, Крым, г. Севастополь, а также Чеченская республика.

Результаты исследования и их обсуждение

Построение имитационной модели предполагает математическое выражение отношений целевых и управляющих факторов (через уравнения регрессии), описание факторов в терминах системной динамики и запуск модели в AnyLogic, проведение экспериментов с исходными данными [11].

Анализ корреляций целевых и управляющих факторов позволил остановиться на шести целевых факторах, имеющих наиболее выраженные связи с Х-ми – это Y1, Y3, Y4, Y7, Y8 и Y9.

Для этих факторов были построены следующие уравнения регрессии:

У1 = 60,7015+ 0,1075 х! 1 + 0,1974-х30+ + 44.1394-х14-0.000492-х32, R² =0,5920,

ГЗ = 0,8779 - 0,0018 • х8+0,0061 •

•х29-0,0112-х7, R = 0,292»

Y1 = 25,6048+0,0311 • х34 + 0,1369 •

-Х15+ 0,1025 х11,7?" =0,2539,

Г4 = 0.02117+0,0000058 x32-0,000075-

•х34+ 0,00032-х11, R² =0,42655,

К8= 14,305-0,225 x28-0,124 x30. R² =0,2596, (5)

Y9 = 40,2709 - 0,1002 • хЗ 1 + 0.0011 x32-

-0,1676-х1-0.276-х22, R² =0,5356.

На данном этапе исследования перед нами не стояла задача интерпретации полученных связей целевых и управляющих факторов, в том числе оценки значимости коэффициентов перед Х-ми, перебор различных управляющих факторов в регрессионных уравнениях был ориентирован на обнаружение «связных» (повторяющихся) факторов для разных Y. Как видно из формул, такими факторами в нашем случае выступают x11 (доля педагогов высшей категории), x30 (инновационная активность организаций), x34 (отношение среднедушевого дохода населения к прожиточному минимуму в регионе) и x32 (расстояния от Москвы до центров регионов), которые встречаются в математических моделях по 2–3 раза.

Однако переход к единой модели, имитирующей процессы в российских регионах, связанные со здоровьем и образованием детей, сопряжен с трудностями учета большого разброса значений факторов в региональных проекциях, включенных в модель. Это заставило нас обратиться к инструменту кластерного анализа для объединения регионов, сходных по своим характеристикам, и последующего моделирования с учетом межкластерных различий.

Для проведения анализа данных и дальнейшей кластеризации была использована аналити-

Перечень управляющих факторов

List of control factors

Table 1

x1 охват детей дошкольным образованием, %; x20 расходы на обязательное медицинское страхование, руб/чел.; x2 доля детей, обучающихся в школах искусств, музыкальных и пр., %; x21 прирост мигрантов нетрудоспособного возраста, %; x3 доля детей в возрасте до 14 лет, систематически занимающихся физической культурой, %; x22 количество жителей с высшим образованием на 1 тысячу человек, чел.; x4 доля выявленных безнадзорных и беспризорных детей, %; x23 отношение числа вузов и филиалов к численности населения на 10000 чел.; x5 средняя наполняемость классов, чел.; x24 отношение числа профессиональных образовательных организаций, осуществляющих подготовку специалистов среднего звена к численности населения на 10000 чел.; x6 доля частных общеобразовательных организаций, %; x25 отношение числа преступлений в отношении несовершеннолетних к численности лиц младше трудоспособного населения, %; x7 доля школ, имеющих столовую или буфет, %; x26 соотношение браков и разводов (на 1000 браков приходится разводов), шт.; x8 доля школ, в которых созданы условия для обучения инвалидов, %; x27 число посетителей театров и музеев на 1000 чел, чел.; x9 среднее число участников клубных формирований в расчете на 1 тыс. человек населения, чел.; x28 жилая площадь на 1 человека, м2; x10 процент обучающихся во 2-3 смены в общей численности обучающихся в государственных (муниципальных) общеобразовательных организациях, %; x29 уровень занятости населения, %; x11 доля педагогов высшей категории, %; x30 инновационная активность организаций, %; x12 число ПК образовательных организаций с доступом к интернету на 100 учащихся, шт.; x31 плотность населения, чел/км2; x13 доля расходов на образование, %; x32 расстояния от Москвы до центров регионов, км.; x14 количество автобусов для перевозки детей (выпуск не более 10 лет) к численности лиц младше трудоспособного населения, %; x33 ВРП на душу населения, руб.; x15 доля детей, отдохнувших в оздоровительных лагерях, %; x34 отношение среднедушевого дохода населения к прожиточному минимуму в регионе, % ; x16 пропускная способность спортивных сооружений, %.; x35 плотность автомобильных дорог общего пользования с твердым покрытием, км путей на 1000 км2 территории; x17 среднее число вакцинированных детей в возрасте 12 мес., чел.; x36 выбросы загрязняющих веществ в атмосферный воздух, отходящих от стационарных источников, тыс. т/чел.; x18 обеспеченность педиатрами (отношение педиатров к численности лиц младше трудоспособного населения), %; x37 сброс загрязненных сточных вод в поверхностные водные объекты, млн. м3/чел.; x19 отношение заработной платы медицинских работников к средней заработной плате региона, %; x38 использование свежей воды, млн. м3/чел. ческая платформа Deductor, с ее помощью осуществлялось также вышеописанное построение регрессионных уравнений. В качестве входных показателей кластеризации были выбраны шесть факторов, сигнализирующих, с одной стороны, о «насыщенности» региональной среды в образовательно-культурном и инфраструктурном планах, а с другой, – о возможностях ее развития (инновационного, экономического) – это факторы х22, х27, х28, х29, х30, х35.

В табл. 2 перечислены регионы, вошедшие в каждый кластер, в алфавитном порядке.

На следующем этапе исследования, прежде чем приступить к моделированию в AnyLogic, выполним проверку нашей модели с шестью целевыми факторами и тринадцатью управляющими факторами на устойчивость и точность.

Для этого сравним данные, полученные в ходе моделирования Y1, Y3, Y4, Y7, Y8 и Y9 по каждому кластеру в отдельности, со средними значениями по кластеру. Результаты приведены в табл. 3. Они охватывают средние значения Y, моделируемые значения Y, а также отклонения моделируемых значений от средних и рассчитаны по всей выборочной совокупности и каждому кластеру в отдельности.

Отклонение расчётных значений управляющих факторов (х) от среднего по кластеру более чем на 10 процентов, вероятно, говорит о снижении устойчивости и точности модели. Для итогового моделирования решено было оставить факторы Y1 и Y7. Максимальное отклонение моделируемого значения Y1 от среднего по кластеру составило 1,62%, а Y7 – 2,16%. У Y3 максимальное отклонение также не превысило 10%, но оно не связано с Y1 и Y7 через управляющие факторы.

Для перехода к имитационному моделированию присутствующие в регрессионных уравнениях управляющие (х) и целевые факторы (Y) были описаны в терминах системной динамики, перекодированы в динамические переменные, параметры и константы [11]. Таким образом, для четырех кластеров будет построена одна имитационная модель, но эксперименты с ней будут запускаться исходя из фактических значений внутри каждого кластера в отдельности.

Данные для имитационного моделирования представлены в табл. 4. Для описания изменения поведения целевых факторов Y1 и Y7 необходимо ввести 16 элементов разного типа (динамическая переменная; выпадающий список, регулируемое значение). Значение по умолчанию регулируемых параметров задается как среднее от данных по 75

регионам (на конец 2015–2016 учебного года).

Фрагмент построенной имитационной модели приведен на рис. Отметим, что данная схема является обобщённой и требует дальнейшей конкретизации. Для построения модели использован программный продукт AnyLogic (© The AnyLogic Company). Имитационная модель позволяет запускать эксперименты, используя бегунки, прикреплённые к переменным. Параметр х32 представлен в виде выпадающего списка, имеющего пять значений, – среднее по России и по четырем кластерам.

Проанализировав результаты эксперимента, представленные в табл. 2, заметим, что значения целевых факторов Y1 и Y7 в кластерах 2 и 3 превышают средние по всей выборке из 75 российских регионов, а в кластерах 1 и 4 оказываются значительно ниже. Соответственно, дальнейшие эксперименты будут проходить для кластеров по разным схемам.

Для кластеров 1 и 4 эксперименты будут связаны с приближением значений целевых факторов к средним значениям по выборке, а для кластеров 2 и 3 – с изменением управляющих факторов на значения среднегодового прироста за предшествующие 5 лет. Среднегодовое отклонение показателей за 5 лет рассчитывалось как среднее от ежегодных относительных отклонений факторов.

Для проведения первой серии экспериментов (с кластерами 1 и 4) воспользуемся надстройкой MS Excel «Поиск решения», результаты представлены в табл. 4. Для роста показателя Y1 (средний балл ЕГЭ по русскому языку) в кластере 1 с 66,95 (среднее по кластеру 1) до 67,47 (среднее по выборке) баллов оптимальными изменениями будут увеличение показателя доли педагогов высшей категории (x11) с 33,965 до 36,7821%; увеличение отношения количества автобусов для перевозки детей к численности лиц младше трудоспособного населения с 0,0645 до 0,0686%, а также увеличение инновационной активности организаций с 6,66 до 6,8592%. Для достижения Y7 (доля детей I–II групп здоровья) среднего значения по выборке, равного 42,9662% вместо 42,3082% при уже определенном значении х11 в 36,7321% и фиксированном значении х34 (труднорегулируемая переменная) необходимо увеличить долю детей, отдохнувших в оздоровительных лагерях (x15), с 37,5236 до 40,2864%.

Результаты экспериментирования с параметром Y1 и Y7 для кластера 4, представленные в табл. 5, интерпретируются аналогично.

Состав территориальных кластеров

Composition of territorial clusters

Table 2

Первый кластер. Регионы с высоким потенциалом	Второй кластер. Регионы с нормальным потенциалом	Третий кластер. Регионы с нормальным потенциалом	Четвертый кластер. Регионы с низким потенциалом
22	10	32	11
Амурская область	Белгородская область	Алтайский край	Кабардино-Балкарская Республика
Астраханская область	г. Москва	Брянская область	Карачаево-Черкесская Республика
Еврейская автономная область	г. Санкт-Петербург	Владимирская область	Республика Адыгея
Забайкальский край	Камчатский край	Волгоградская область	Республика Ингушетия
Иркутская область	Липецкая область	Вологодская область	Республика Калмыкия
Кемеровская область	Магаданская область	Воронежская область	Республика Северная Осетия – Алания
Кировская область	Московская область	Ивановская область	Республика Тыва
Красноярский край	Пензенская область	Калининградская область	Самарская область
Курганская область	Республика Татарстан (Татарстан)	Калужская область	Ставропольский край
Мурманская область	Чувашская Республика – Чувашия	Костромская область	Ханты-Мансийский автономный округ – Югра
Новосибирская область		Краснодарский край	Ямало-Ненецкий автономный округ
Омская область		Курская область
Пермский край		Ленинградская область
Приморский край		Нижегородская область
Республика Бурятия		Новгородская область
Республика Карелия		Оренбургская область
Республика Коми		Орловская область
Республика Саха (Якутия)		Псковская область
Республика Хакасия		Республика Башкортостан
Свердловская область		Республика Марий Эл
Томская область		Республика Мордовия
Хабаровский край		Ростовская область
		Рязанская область
		Саратовская область
		Смоленская область
		Тамбовская область
		Тверская область
		Тульская область
		Удмуртская Республика
		Ульяновская область
		Челябинская область
		Ярославская область

Table 3

Целевые факторы	Суммарно по 75 регионам	Кластер 1	Кластер 2	Кластер 3	Кластер 4
Y1	67,4718	67,0032	67,894	68,2576	64,3842
Y1*	67,6281	66,9531	68,9914	68,2177	64,751
∆	0,23%	-0,07%	1,62%	-0,06%	0,57%
Y3	0,0972	0,096	0,1143	0,1138	0,062
Y3*	0,1008	0,096	0,1143	0,1138	0,062
∆	3,70%	0,00%	0,00%	0,00%	0,00%
Y4	0,0216	0,0305	0,0206	0,0148	0,0276
Y4*	0,0223	0,031	0,0192	0,0164	0,0206
∆	3,24%	1,64%	-6,8%	10,81%	-25,36%
Y7	42,9662	41,4136	45,93	43,9559	39,6857
Y7*	42,9703	42,3082	44,9637	43,5236	39,5093
∆	0,01%	2,16%	-2,1%	-0,98%	-0,44%
Y8	7,5729	7,8332	6,52	7,3781	8,8636
Y8*	7,6951	8,1963	6,2701	5,0087	13,9019
∆	1,61%	4,64%	-3,83%	-32,11%	56,84%
Y9	19,1358	23,1864	16,47	18,2406	15,4032
Y9*	7,6862	23,6	-69,7302	18,316	17,1234
∆	-53,83%	1,78%	-423,38%	0,41%	11,17%

Примечание: * Yn – среднее значение по выборке из 75 регионов/n-го кластера; Yn*– результат моделирования со средним значением выборки из 75 регионов/ в кластере n; ∆ – отклонение моделируемого значения в кластере n от среднего по выборке из 75 регионов/в кластере рассчитывается по формуле:Д= (^^)*100%

Элементы модели «Здоровье и образование детей в российских регионах» и исходные значения для проведения экспериментов

Elements of the model «Health and education of children in the regions of Russia», and the initial values for the experiments

Table 4

Фактор	Обозначение в модели, элемент модели, единица измерения	Значение по умолчанию	Диапазон значений
Средний балл ЕГЭ по русскому языку	Y1_ball_USE, Динамическая переменная, балл	Определяется по формуле 1	0–100
Численность детей I-II групп здоровья по отношению к численности населения младше трудоспособного возраста	Y7_health_group, Динамическая переменная, %	Определяется по формуле 4	0–100
Численность учителей государственных и муниципальных общеобразовательных организаций (без вечерних (сменных) общеобразовательных организаций)	num_pegagogy, Параметр, регулируемое значение, чел	12 690	1 100– 58 800
Численность педагогов высшей категории	ped_hig_categor, Параметр, регулируемое значение, чел.	5 087	21–24764
Доля педагогов высшей категории	x11_pegagogy, Динамическая переменная, %	ped_hig_categor / num _pegagogy *100	0–100
Численность детей, отдохнувших за лето в детских оздоровительных лагерях	rested_children, Параметр, регулируемое значение, чел.	56 776	1439– 208 605
Общая численность обучающихся в образовательных организациях, реализующих программы общего образования	minors, Параметр, регулируемое значение, чел.	174 613	6 091– 883 672
Отношение числа детей, отдохнувших в оздоровительных лагерях, к числу обучающихся детей всего	x15_rested_children, Динамическая переменная, %	rested_children/ minors*100	0–100
Среднедушевые денежные доходы населения	income_population, Параметр, регулируемое значение, руб.	27 152,27	14 216– 66 869
Величина прожиточного минимума, установленная в субъектах Российской Федерации за IV квартал 2015 г.	living_wage, Параметр, регулируемое значение, руб.	9 759,49	7 775– 18 427
Отношение среднедушевого дохода населения к прожиточному минимуму в регионе	x34_average_income, Динамическая переменная, %	income_ population/ living_wage *100	77–860
Доля числа автобусов для перевозки детей (эксплуатация не более 10 лет) к числу лиц младше трудоспособного населения	x14_buses_children, Параметр, регулируемое значение, %	0,04548	0,002–0,115
Организации, выполнявшие научные исследования и разработки	NIR_Enterp, Параметр, регулируемое значение, шт.	53	2–811
Число предприятий и организаций	Enterpise_all, Параметр, регулируемое значение, шт.	6 814	345– 1 171 307
Инновационная активность организаций	X30_innovation, Динамическая переменная, %	NIR_Enterp / Enterpise_all *100	0–235
Расстояния от Москвы до центров регионов	x32_distance, Параметр, выпадающий список, км	1 664,8	1 664 3 174,77 1 619,5 619,599 1 613,1818

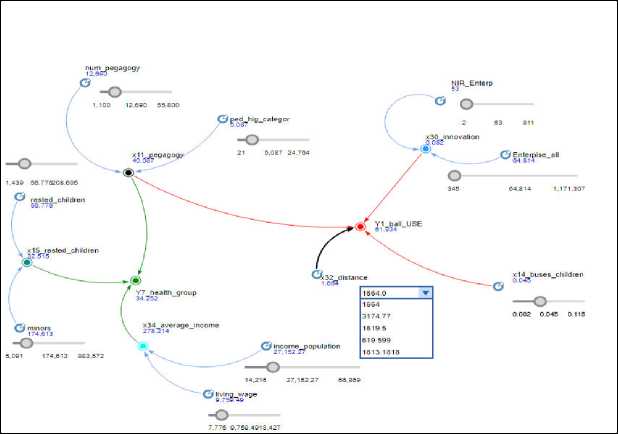
Рис. Фрагмент модели системной динамики «Здоровье и образование детей в российских регионах»

Fig. Fragment of the system dynamics model «Health and education of children in Russian regions»

Таблица 5

Результаты экспериментирования с параметрами Y1 и Y7 для кластеров 1 и 4

Results of the experiment with parameters Y1 and Y 7 for clusters 1 and 4

Table 5

Целевой фактор	Фактор	Кластер 1		Кластер 4
		Среднее значение по кластеру	Оптимальное значение фактора	Среднее значение по кластеру	Оптимальное значение фактора
Y1	x11	33,965	36,7321	28,198	49,5150
	x14	0,0645	0,0686	0,0249	0,0317
	x30	6,6636	6,8592	3,609	4,2502
	x32	3174,7727	3174,7727	1613,18	1613,18
Y7	x11	33,965	36,7321	28,1980	49,5150
	x15	37,5236	40,2864	22,9950	32,3143
	x34	259,9677	259,9677	252,93	252,93

Таблица 6

Исходные значения экспериментирования для кластеров 2 и 3

Table 6

Initial experimental values for clusters 2 and 3

Целевой фактор	Управляющие факторы	Кластер 2		Кластер 3
		Среднее значение фактора по кластеру	Значение фактора с учетом тенденции изменения	Среднее значение фактора по кластеру	Значение фактора с учетом тенденции изменения
Y1	x11	41,8580	42,6952	28,198	49,5150
	x14	0,0308	0,0308	0,0249	0,0317
	x30	16,3500	16,4514	3,609	4,2502
	x32	1619,5000	1619,5000	1613,18	1613,18
Y7	x11	41,8580	42,6952	28,1980	43,6415
	x15	35,1350	33,9439	22,9950	36,7119
	x34	329,853	315,8013	252,9300	265,3018

Результаты эксперимента 2 с параметрами Y1 и Y7 для кластеров 2 и 3

Table 7

Results of experiment 2 with parameters H1 and H7 for clusters 2 and 3

Показатель	Кластер 2		Кластер 3
	Y1	Y7	Y1	Y7
Исходное значение	68,9914	44,9637	68,215	43,5236
Результат эксперимента	68,118	44,4494	69,8677	42,6829
Фактическое значение	68,6948	45,1073	68,245	43,5236
Отклонение моделируемого значения от фактического	-0,84%	-1,46%	2,38%	-1,93%

Результаты использования имитационной модели по кластерам

The results of application of clusters simulation model

Для проведения второй серии экспериментов с кластерами 2 и 3, где средние значения Y1 и Y7 по кластеру выше средних значений по выборке, было решено изменять значения управляющих факторов на величину среднегодового прироста показателя за период с 2010 по 2015 гг.

Значения фактора с учетом тенденции его изменения мы берем в качестве исходных данных для проведения эксперимента 2 с кластерами 2 и 3. Результаты эксперимента 2 представлены в табл.

7. В качестве фактических значений целевых факторов приведены данные по среднему баллу ЕГЭ по русскому языку и доле детей I–II групп здоровья за 2016–2017 учебный год.

Отклонения моделируемых значений целевых факторов Y1 и Y7 от их фактических значений за 2016-2017 уч. г. изменяются в пределах от -1,93 до + 2,38%, что в целом говорит об устойчивости сконструированной модели.

Заключение

С использованием инструментов математикостатистического анализа (корреляционный, регрессионный, кластерный анализы) была построена модель «Образование и здоровье детей в российских регионах», включающая 2 целевых и 6 управляющих факторов. Целевыми факторами обозначены средний балл ЕГЭ по русскому языку и доля детей I–II групп здоровья. Управляющие факторы были разделены на константы (расстояния от Москвы до центров регионов), труднорегулируемые (отношение среднедушевого дохода населения к прожиточному минимуму в регионе, инновационная активность организаций) и регулируемые (доля педагогов высшей категории, доля детей, отдохнувших в оздоровительных лагерях, обеспеченность детей автобусами) факторы.

Для четырех выделенных кластеров эксперименты с моделируемыми значениями проводились по двум схемам. Для кластеров 1 и 4, в которых значения Y1 и Y7 в целом ниже средних по выборке, была использована надстройка MS Excel «Поиск решения», а моделируемыми значениями целевых факторов были средние значения по всей выборочной совокупности. Эксперименты показали, что для достижения значений целевых факторов, равных средним по выборке из 75 регионов, необходимо существенное изменение (для кластера 4 – более чем на 20%) фактора x11 «доля педагогов высшей категории». При этом среднегодовое отклонение показателя за последние три года немного превысило 2%. Это демонстрирует важность работы по повышению квалификации педагогов, оказывающей влияние не только на повышение качества образования (в нашей модели – это средний балл ЕГЭ), но и на возможное увеличение доли детей I–II групп здоровья.

Закрытие малокомплектных школ в сель-

ской местности актуализирует задачу расширения парка школьных автобусов. В нашей модели прирост обеспеченности детского населения автобусами для их перевозки по кластеру 1 составил 6,4%, а по кластеру 4 – 27,3%. Также сильное влияние на средний балл ЕГЭ оказывает общий образовательно-интеллектуальный потенциал региона, который мы пытаемся выявить за счет статистического показателя «инновационная активность организаций» (х30). Отклонение моделируемого значения х30 от среднего значения по кластеру 1 составило +2,9%, а по кластеру 4 – +27,8%.

Вполне объяснимо на повышение значения Y7 (доля детей I–II групп здоровья) влияет показатель отдыха детей в оздоровительных лагерях (х15). Функция поиска оптимальных значений в отношении переменной х15 дала для кластера 1 прирост 7,4%, а для кластера 4 –40,5%. То есть в целом регионы четвертого кластера требуют больше ресурсных затрат для достижения заданных значений целевых показателей.

Для кластеров 2 и 3 эксперимент был связан с преобразованием значений управляющих факторов с учетом тенденции изменения за последние 5 лет. Эксперименты с кластерами 2 и 3 подтвердили прогностическую ценность модели и возможность использования в качестве исходных данных значений с учетом тенденции их трансформации. Имеющиеся данные по среднему баллу ЕГЭ по русскому языку и доле детей I–II групп здоровья за 2016–2017 учебный год позволили сравнить смоделированные значения Y1 и Y7 с фактическими.

Дальнейшая работа с построенной имитационной моделью будет связана с ее дополнением другими параметрами и проведением экспериментов со средними значениями целевых и управляющих факторов в отдельных российских регионах.

Низкие значения уровня объясненной регрессии говорят о необходимости подключения других исследовательских инструментов для выяснения управляющих факторов и силы их влияния, например, метода экспертных оценок.

Работа выполнена при финансовой поддержке гранта РФФИ (проект № 16-36-60041).