Жидкокристаллический оптический затвор для витражей и окон

В настоящее время разнообразие материалов, использующихся в производстве, промышленности, а также в технологиях, трудно переоценить. Ученые и инженеры работают над созданием новых материалов, которые смогут расширить технические возможности и позволят создать принципиально новые приборы, которые можно применить в различных отраслях человеческой деятельности [1–26]. К таким материалам относятся и наноматериалы. Как известно, наноматериалы – это материалы, которые были созданы на основе наночастиц или с использованием нанотехнологий. Их характерные размеры лежат в пределах от 1 до 100 нанометров. С приставкой нано- известны трубки, волокна, кластеры, ленты,

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ дисперсии, пленки, и этот ряд можно продолжить. Отдельный огромный пласт задач решается с использованием углеродных материалов (фуллеренов, графенов, трубок, алмазов, волокон). Разработка и поиск новых наноматериалов ведется не одно десятилетие, что открывает перспективы развития технологий. Упомянутые выше наноматериалы имеют кристаллическую структуру.

В строительстве, а также в декоре широко используется, например, жидкое стекло. Это очень плотная и вязкая субстанция при рабочей температуре 95–98оС, после нанесения на поверхность твердеет. Применяется для гидроизоляции, например, фундамента, имеет хорошие адгезионные характеристики, материал устойчив к термическим воздействиям, не восприимчив к влаге, нетоксичен, огнеупорный, имеет антистатические и антисептические свойства, обработанная поверхность имеет долгий срок службы. К недостаткам можно отнести возможность получения ожогов при контакте с кожей из-за наличия в составе щелочи; быстро высыхает, поэтому необходимо иметь навык работы с ним; эффектив- но применяется для бетона и дерева, но разрушает структуру кирпича.

Одним из материалов, который относят к наноматериалам из-за малости размеров молекул (от 5 до 30 Å) и который нашел применение в науке, технике, в разработке различных инженерных решений, является жидкий кристалл (ЖК). Жидкий кристалл имеет свойства одновременно твердого тела и жидкости. Он вязок и текуч, как жидкость, но при этом имеет строгий ориентационный порядок молекул, как твердое тело. Это органические вещества, которые содержатся в живом организме (например, холестерин), и поэтому жидкие кристаллы успешно применяются в медицине для создания приборов и методов ранней диагностики болезней, тонкие пленки ЖК рассматривают как модели мембран клеток [19]. Жидкие кристаллы используют в технике для создания мониторов, табло, различных датчиков, сенсоров, как для систем отображения информации, так и в качестве «рабочего вещества» для контроля давления, вибраций, уровней жидких или сыпучих веществ [1–24].

Рис. 1. Текстуры в жидких кристаллах, наблюдаемые под микроскопом

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Уникальные физические свойства жидких кристаллов делают их чувствительными к внешним воздействиям. Так, при нагревании, подключении электрического или магнитного полей, различного рода механических действиях (сдвиг, изгиб, кручение) жидкие кристаллы демонстрируют множество различных эффектов, на принципах которых основана работа уже созданных приборов, а перспективы их использования безграничны.

Жидкие кристаллы демонстрируют очень необычные и красивые картины, которые можно использовать для декора и дизайна интерьера (рис. 1, фотографии взяты из открытых источников).

Автор статьи имела опыт творческого сотрудничества с кафедрой дизайна Уфимского государственного университета экономики и сервиса. Фотографии, полученные при проведении физического экспери- мента с жидкими кристаллами, были использованы при оформлении интерьера. В результате такой совместной работы были проведены выставки в г. Уфе в художественной галерее «Academia» («Творчество жидких кристаллов»), а также в Государственном центре современного искусства в г. Москве («Физическая картина мира: визуальные образы жидких кристаллов»).

Дизайнеры и архитекторы находятся в постоянном поиске новых решений в архитектуре и цвете. Черпать идеи можно, в частности, изучая строение вещества, вооружившись микроскопом (рис. 2, фотографии взяты из открытых источников).

Жидкие кристаллы имеют анизотропию физических свойств, т.е. они проявляются по-разному при воздействии на кристалл в различных направлениях. Анизотропия свойств обусловлена также строением

Рис. 2. Футуристические архитектурные и цветовые решения

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ молекул ЖК. По форме молекулы жидкого кристалла можно аппроксимировать в виде банана, диска или палочки [25, 26]. Мы будем рассматривать жидкие кристаллы с молекулами вытянутой формы в диаметре порядка 5 Å, длиной порядка 30 Å.

Вследствие анизотропии физических свойств и формы молекул жидкие кристаллы демонстрируют многообразие различных эффектов, которые не наблюдаются в жидкостях или твердых кристаллах. В твердых телах наблюдается эффект двойного лучепреломления при механической деформации двутавровой балки. Если взять тонкий слой жидкого кристалла, помещенного между стеклами, посмотреть в окуляр микроскопа, поляроиды которого скрещены, то мы увидим темное поле. При действии на кристалл внешним полем можно добиться того, что слой кристалла будет пропускать световой пучок. То есть при определенных условиях ячейка с жидким кристаллом либо пропускает свет, либо нет, таким образом, она может использоваться как оптический затвор.

В твердых кристаллах известен пьезоэлектрический эффект [25, 26], который заключается в возникновении электрического поля при механической деформации. Аналогичный эффект имеет место в жидком кристалле, он наблюдается при возникновении, например, сдвиговых деформаций, и называется флексоэлектрическим эффектом («флексо» – изгиб). В результате изгибных деформаций в жидком кристалле появляется поверхностная поляризация, кроме того, клиновидная или серповидная форма молекул ЖК приводит к возникновению локальной деформации поля директора и (директор – вектор, характеризующий преимущественное направление ориентации молекул ЖК).

Если молекулы кристалла ориентированы в горизонтальной плоскости, то такая ориентация называется планарной; если молекулы ориентированы вертикально, то такая ориентация называется гомеотропной.

В данной статье представлены результаты экспериментального исследования эффекта, наблюдаемого в жидких кристаллах, тонкие слои которых могут служить оптическим затвором (шторкой или жалюзи) для витражей или окон зданий и сооружений.

МАТЕРИАЛЫ И МЕТОДЫ

Материалы

Для экспериментального исследования флексоэлектрического эффекта использовались жидкие кристаллы нематического типа (НЖК), основные параметры которых приведены в табл. 1.

Методы

Исследовались образцы с гомеотропной ориентацией молекул толщиной h от 10 до 100 мкм методом двойного лучепреломления. Частота сдвигового воздействия порядка 1 кГц.

Ячейка с жидким кристаллом была изготовлена из двух стеклянных пластин в виде плоского конденсатора (рис. 3), между стеклами помещались прокладки, которые и задавали толщину образца.

На подложки нанесено проводящее покрытие из металлического хрома, оно позволяло получить необходимую ориентацию молекул ЖК. Для поддержания нужной температуры существования ме-

Таблица 1

Физические параметры жидких кристаллов

Жидкий кристалл	Температура мезофазы, оC	е 11, 10–4 ед. СГСЕ/см	е 33, 10–5 ед. СГСЕ/см	Дипольный момент, p , D	Диэлектрическая анизотропия, εα
цианофениловый эфир гептилбензойной кислоты (ЦФЭГБК)	45 o    56 o K — N — I	5,5	3	~4,5	~19
нитрофенилоктилоксибен-зоат (НФООБ)	oo K4—5 А —61 I 68 o — I	5,0	1	~4,1	> 0
n-метоксибензилиден-n-бутиланилин (МББА)	18 o    42 o K — N — I	4,5	102	~2,6	< 0
будетилгептаноилазокси-бензол (БГАОБ)	20 o    71 o K — N — I	4,0	30	~3	> 0

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

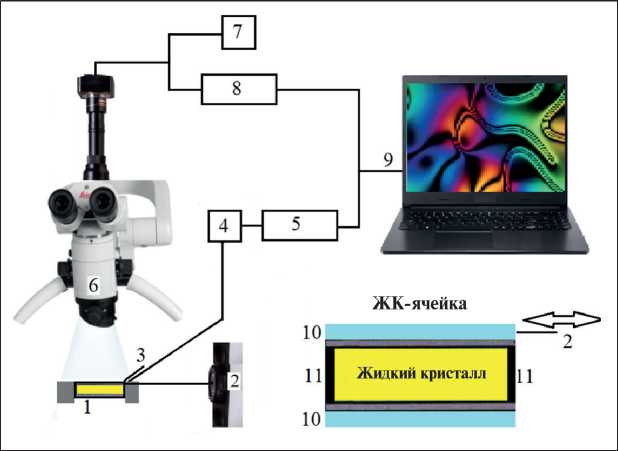
Рис. 3. Элементарная установка для экспериментального детектирования флексоэлектрического эффекта в ЖК:

• 1    – ячейка-конденсатор с ЖК;

• 2    – источник колебаний (сдвиг);

• 3    – термопара; 4 – милливольтметр постоянного тока; 5 – аналогоцифровой преобразователь;

• 6    – микроскоп; 7 – вольтметр постоянного тока; 8 – селективный усилитель; 9 – компьютер;

• 10    – стеклянные подложки;

• 11    – прокладки

зофазы ячейка нагревалась, температура контролировалась термопарой.

Образцы помещали на предметный столик оптического микроскопа. Луч света проходил через экспериментальную ячейку, и его переменная компонента регистрировалась спектрофотометрической приставкой. Для регистрации постоянной компоненты оптического сигнала использовали милливольтметр постоянного тока. Сбоку от предметного столика микроскопа располагался источник сдвиговых колебаний, который соединялся с ЖК-ячейкой при помощи тонкого волновода. Методика экспериментальных исследований подробно описана в работах [6, 8].

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Будем исследовать флексоэлектрический отклик ЖК системы на возмущение сдвигового типа, при котором одна из ограничивающих поверхностей слоя совершает периодические колебания со скоростью V. Будем также рассматривать ЖК слои только с однородной ориентацией молекул.

Согласно геометрии задачи директор направлен вертикально параллельно оси Z , вектор скорости колебаний пластины – горизонтально по оси X . Ориентация молекул жидкого кристалла в объеме характеризуется углом θ . Уравнение, описывающее распределение угла θ вдоль оси Z в общем виде, можно записать [26]:

pi)o

6 =--- exp 4iQ

V2

—— b(z -5)

cos

V2

— b(z -<5)

COStot , (1)

где η1, η4 – коэффициенты вязкости; δ – расстояние, на котором директор имеет отклонение от первоначальной ориентации; реальная часть корней характеристического уравнения: b~[(η4 ρω2)/ (η3 K33)]1/2; K33 – коэффициент упругости; ω – частота периодического сдвига.

Согласно уравнению (1), между подвижной и неподвижной подложками ЖК-ячейки распространяется упруго-вязкая волна, которая приводит к возмущению начальной гомеотропной ориентации поля директора (рис. 4 б).

Причем профиль искажения директора в плоскости, об р азуемой вектором скорости и волновым вектором Q , представляет из себя деформацию В-типа (bend), а значит в объеме нематического жидкого кристалла может индуцироваться флексоэлектрическая поляризация также только В-типа, вектор которой лежит в плоскости ЖК слоя. Отсюда непосредственно вытекает, что разность потенциалов между обкладками ячейка-конденсатор должна быть равна нулю, т.к. проекция поляризации на нормаль к слою равна нулю. Однако в действительности между проводящими подложками при возмущении начальной ориентации сдвигом регистрируется переменная ЭДС, в которой можно выделить как первую, так и вторую гармоники U_1ω и U_2ω (рис. 4 а, в).

Рассмотрим зависимость первой гармоники U_1ω от величины скорости сдвига (рис. 4 а, ω = 1 кГц), например, в НЖК МББА при заданной температуре Т = 25^оС. В этой зависимости по оси абсцисс выделим две области, характерные для поведения U_1ω : 0 <  υ <  υ _c и υ >  υ _c, где υ _c – значения скорости, при которой происходит скачок величины U_1ω и изменение тангенса угла наклона U_1ω относительно оси υ . В первой области первая гармоника слабо зависит от величины скорости или, что то же самое, от амплитуды смещения а . При υ ≈ υ _c испытывает скачок. Поляризационно-оптические исследования показали, что при этом в слое индуцируется стационарный

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ аб

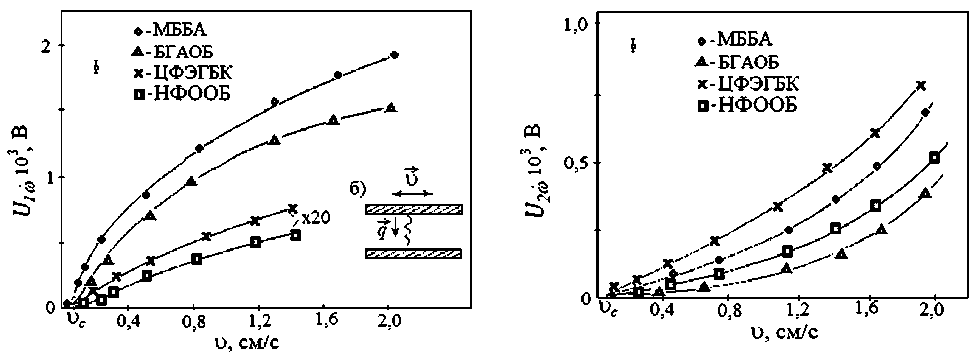
Рис. 4. Зависимость первой гармоники U_1ω от скорости осцилляций: а) иллюстрация ориентационного искажения в объеме ЖК под действием периодического сдвига; б) зависимость второй U_2ω гармоники от скорости осцилляций (температуры существования нематической фазы T_N ЖК: 25^оС (МББА), 25^оС (БГАОБ), 48^оС (ЦФЭГБК), 3^оС (НФООБ))

наклон молекул НЖК θ_c , который, по-видимому, и приводит к резкому возрастанию величины гармоники.

Не уточняя подробности, укажем, что причины появления стационарного распределения угла директора θ_c в такой геометрии могут быть разнообразные, например, из-за нелинейности уравнений, описывающих поведение жидких кристаллов по скорости движения [25], или из-за нестрого линейного движения подвижной пластины в одной плоскости, которое становится эллиптическими [26]. В данном случае будем опираться на экспериментальный факт наличия такого распределения и покажем, что при этом появляется компонента поляризации, перпендикулярная слою ЖК.

Рассмотрим случай, когда направление оси Х совпадает с направлением колебания пластины, ось Z перпендикулярна слою НЖК. Тогда можно воспользоваться уравнением (2), и поляризация по оси Z при малом наклоне директора n к оси будет выражаться:

Э9д

Pz = e33 [rotn X n\z % e33svn8c——exp(iwt), (2) oz где θd – амплитуда колебаний директора. Из этого выражения следует, что при ненулевом значении стационарного угла наклона молекул жидкого кристалла θc между проводящими подложками возникает переменная разность потенциалов, связанная с флексоэлектрическим эффектом. Для определения величины наклона θc в слое исследовались акусто-оптические эффекты – модуляция поляризованного света ориентационными возмущениями в ячейке с ЖК (рис. 5).

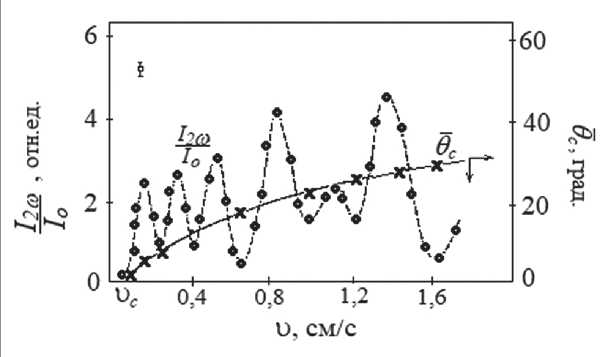
Рис. 5. Зависимости (о) – степени модуляции интенсивности прошедшего поляризованного света через ячейку с ЖК МББА; (×) – и н дуцируемого сдвигом угла наклона 9_c от скорости сдвига υ

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

Относительная величина второй гармоники I_2ω / I_o в зависимости от абсолютного значения скорости осциллирует. Из чего делаем вывод, что в ячейке индуцируется постоянный наклон директора относительно оси Z , т.к. минимумы интенсивности соответствуют набегу разности фаз между обыкновенной и необыкновенной световыми волнами, равной ∆ = πn ( n = 1,2,3,…). Находим зависимость угла наклона от скорости колебания подвижной пластины (рис. 5). Зная величин у среднего угла 0_с и амплитуду девиации директора в_d , можно определить величины флексокоэф-фициентов е ₃₃ исследуемых веществ, т.к. измеряемая величина первой гармоники следующим образом зависит от перечисленных параметров:

h

Vi_M ^ J P_zdz = e₃₃9_c0™ exp(iwt) h.           (3)

Выр а жение (3) верно при условии малости углов 0_c и 0 d , 0_c > 0_d , а также в случае, если | θ_c ( z )– 0_c | << 1, т.е. стациона р ное отклонение θ_c ( z ) слабо отличается от среднего 0_c [26], θ_d^max – максимальная величина амплитуды колебания директора в слое, которая связана со средним значением 0_d измеряемой в эксперименте по амплитуде модуляции светового потока. Исходя из формулы (1), 0 d^m и 0_d связаны следующим образом:

h

9d^j 6ddz = e^W1, где λ = | q| – декремент затухания упруго-вязкой волны.

Тогда выражение (3) запишется в виде:

^iti ^ e33ec0d(Ah2)exp(iwt). (4)

Наличие достаточно большой величины флек-сомодулей делает ЖК перспективным в отношении возможности регистрации ими акустических колебаний и разработки акустических преобразователей. Но для этого, помимо существования прямого флексоэлектрического эффекта, необходимо знать амплитудно-частотную характеристику сигналов, генерируемых вследствие сдвиговых возмущений, создаваемых колебаниями одной из подложек.

Исследования показали, что частотная характеристика сигнала U_1ω (рис. 6) (скорость сдвига = const), например, в МББА аналогична зависимости U_1ω ( ω ), полученной при возмущениях изгибного типа. Значит, реально ячейки подобного типа могут быть использованы в качестве детекторов акустических колебаний низкочастотной области от 20 до 1500÷2000 Гц, хотя имеются данные об использовании аналогичных конструкций для регистрации звуковых полей с помощью светового луча – зонда до частот ω~ 10÷15 кГц.

Перейдем теперь к рассмотрению второй гармоники. Как было показано выше, появление второй гармоники связано с ориентационной модуляцией поляризованного поверхностного слоя – поверхностной поляризации упруго-вязкой волной, что ведет к периодическому изменению емкости этого слоя, проявляющееся в виде генерации поверхностных зарядов на удвоенной частоте возмущения. То есть появление второй гармоники является пороговым, причем пороговое значение скорости υ_c ~8 мм/c возникновения U_2ω ( ω ) совпадает с появлением стационарного наклона молекул в слое. Однако имеются отличия в соотношении сигналов U_1ω и U_2ω .

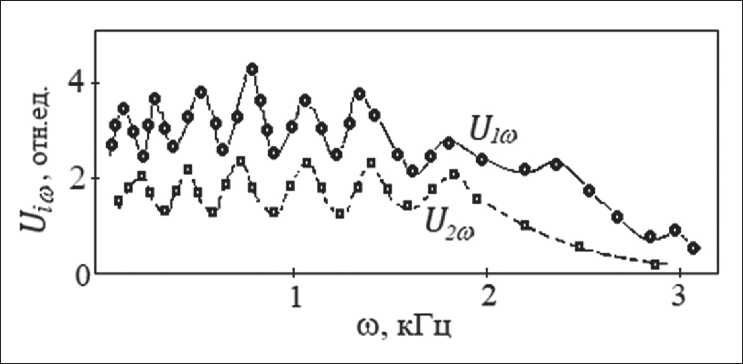
Рис. 6. Частотные зависимости U _{1 ω} и U _{2 ω} гармоник для МББА ( T_N = 25^оС)

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

При сдвиге U_1ω >  U_2ω , что говорит о том, что е ₃₃ >  е ₁₁, например, в МББА и БГАОБ.

Экспериментальным изучением механизмов молекулярно-ориентационной поляризации жидких кристаллов, возбуждаемой акустическим возмущением, было установлено, что в одноосных кристаллах, какими являются большинство нематиков, имеются два флексоэлектрических коэффициента е ₁₁ и е ₃₃. Причем в общее значение коэффициента е ₁₁ дают вклады как диполи, так и квадруполи, хотя и в разном «весовом» соотношении. Такой вывод является результатом анализа температурных зависимостей первой гармоники ЭДС U_1ω и акустоопти-ческих эффектов. Однако вопрос о «весовых вкладах» перечисленных механизмов во флексокоэффициент е ₃₃ остается открытым. В связи с этим необходимо исследование температурных зависимостей флек-сомодуля е ₃₃. Для этого изучим температурное поведение ЭДС, индуцируемой на частоте первой гармоники, а также температурные зависимости величины постоянного угла наклона директора θ_c , индуцируемого сдвиговыми колебаниями одн о й из подложек, и амплитуды колебания директора 9 d .

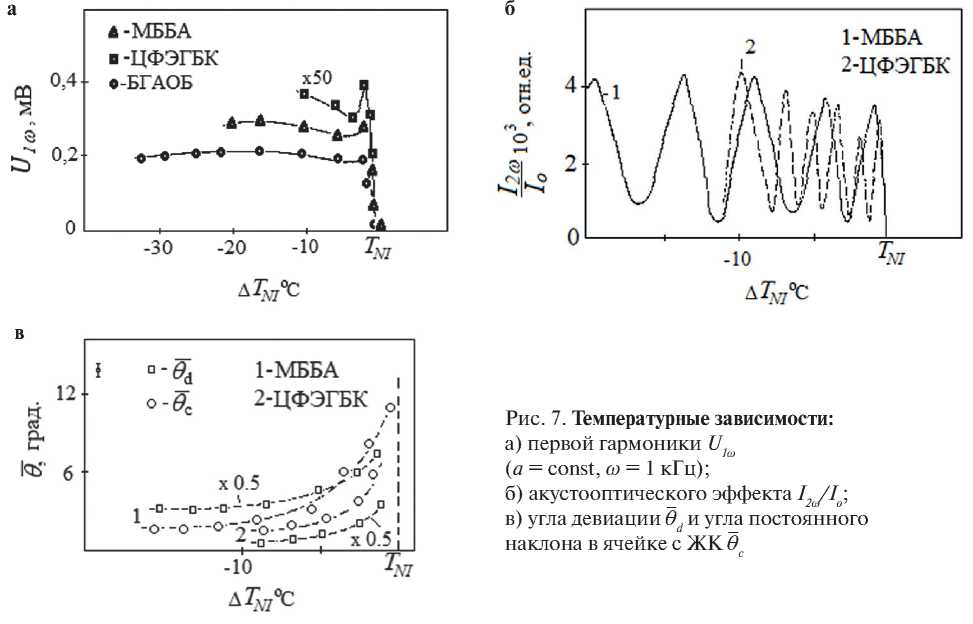
Рассмотрим температурную зависимость U1ω, например, в НЖК МББА (рис. 7 а). Вдали от фазового перехода нематик – изотропная жидкость сигнал, регистрируемый на первой гармонике, ведет себя достаточно регулярно и объяснимо с точки зрения феноменологии, т.е. его величина, уменьшаясь, может быть функцией параметра порядка S, как предсказывает теория флексоэлектрического эффекта. Однако при приближении к фазовому переходу регрессия сигнала U1ω прекращается, а затем значение его возрастает вплоть до температурного перехода нематик – изотропное состояние TNI, что уже необъяснимо в рамках теории. Для понимания такого поведения обратимся к формуле (4). Из нее следует, что величина сигнала U1ω пропорциональна флек-сокоэффициенту е33, среднему постоянному углу c наклона в слое ЖК и амплитуде колебания директора 9d, которые так же, как и модуль е33 могут быть зависимыми от температуры. Отметим, что в данном случае экспериментально параметры 9c ивd выбирались малыми, хотя 9c >9d. Отсюда, получив зависимости 9c (Т) и 9d (Т), можем построить температурные зависимости е33(Т).

Ранее было установлено, что в ячейке с НЖК, имеющей начальную однородную гомеотропную ориентацию, индуцируется сдвигом некоторый постоянный наклон директора 9_c (рис. 7). Выберем по оси абсцисс такое значение скорости, чтобы вследствие наличия наклона при прохождении слоя ЖК поляризованным светом разность фаз ∆ оставалась меньше π , и посмотрим, как будет зависеть вторая гармоника оптического сигнала I_2ω / I_o от температуры (рис. 7 б).

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ

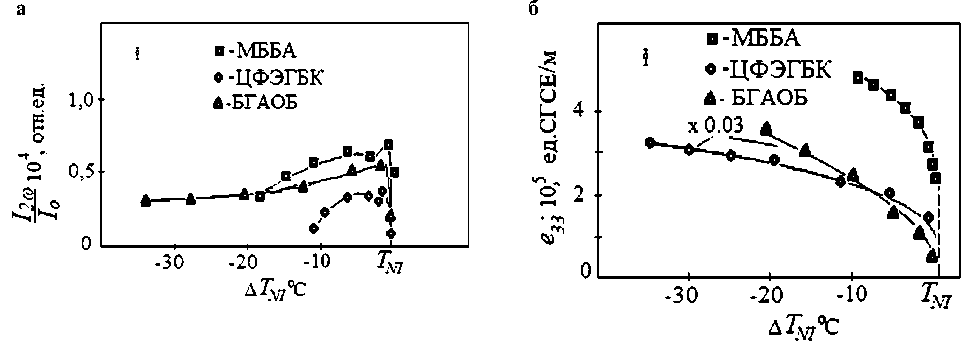
Рис. 8. Температурные зависимости величины: а) акустооптического эффекта I_2ω / I_o ( а = const, ω = 1 кГц); б) флексоэлектрических коэффициентов е е ₃₃ ЖК (МББА, БГОАБ, ЦФЭГБК)

Следует обратить внимание на осциллирующий характер зависимости относительной интенсивности прошедшей необыкновенной волны I_2ω / I_o . Поскольку начальная разность фаз ∆ <  π , то подобное поведе н ие может быть только следствием возрастания угла о_c , т.к. другой параметр – оптическая анизотропия ∆ n ( T ) – уменьшается с приближением к фазовому переходу, как функция параметра порядка S .

Можно оценить, во сколько раз изменяется угол при приближении к температуре перехода нематическое – изотропное состояния T_NI . Зависимость I_2ω / I_o ( T ) имеет пять минимум о в, а т.к. 9_c ²~ πn (где n – количество минимумов), то 9_c ~√ n ~2,3 раза. В действительности, если учесть поправку на температурное изменение оптической анизотропии, получим скорректированную зависимость 9_c ( T ) (рис. 7 в), значение угла при этом возрастает в 4, 5 раза, что согласуется с результатом работы [25] для МББА. Кроме того, по огибающей I_2ω / I_o ( T ) можно судить о зависимости величины осцилляций директора, т.к. значения максимумов пропорциональны квадрату амплитуды директора 9_d ², которая к фазовому переходу также возрастает. Для проверки этого результата изучим температурное поведение величины I_2ω / I_o ( T ) при условии, что ∆ <<  π , когда величина постоянного наклона 9_c ≈ 0, т.е. директор совершает колебания под действием периодического сдвига около начального гомеотропного состояния (рис. 8).

Величина I2ω/Io(T), как и следовало ожидать, к фазовому переходу возрастает, что объясняется ростом вd. Отсюда, зная температурные изменения величин, входящих в формулу для U1ω (4), получим зависи- мости флексокоэффициентов е33 для исследуемых веществ (рис. 8 б). Обсудим эти зависимости.

Можно отметить, что функциональное поведение е ₃₃( Т ) в этих ЖК, а точнее в их нематической фазе, описывается общей зависимостью от параметра порядка S как e ~ α S + β S ². Все значения весовых коэффициентов существенно отличаются для различных НЖК, но согласуются с данными, полученными для модулей е ₁₁ методом изгибных колебаний. Для МББА α~0,1, β~0,9; для БГАОБ α~0,3, β~0,7; а для ЦФЭГБК, НФООБ, ОЦБ α~1,0, β~0. Значения α и β для МББА указывают на возникновение дипольного механизма флексоэлектрической поляризации. В случае же ЦФЭГБК α~1, а β~0, это означает, что в данном случае имеет место квадрупольный характер флексополяризации.

ЗАКЛЮЧЕНИЕ

Таким образом, в статье рассмотрен флексоэлектрический эффект, наблюдаемый в тонких слоях нематических жидких кристаллов с гомеотропной ориентацией молекул, помещенных между двумя стеклянными пластинами. Возникновение эффекта имеет пороговый характер, критическая скорость деформации около 8 мм/с. Рассмотрены условия и параметры воздействия (амплитуда сдвига, температура образца) на ячейку–конденсатор для различных жидких кристаллов. Предлагается использовать полученные результаты для создания оптического затвора (шторка) для витражей или окон зданий и сооружений.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ УЧЕНЫХ И СПЕЦИАЛИСТОВ