Знаковый алгоритм анализа спектра амплитуд и восстановления гармонических составляющих сигналов в условиях присутствия некоррелированных фоновых шумов

ВВЕДЕНИЕ. ПОСТАНОВКА ЗАДАЧИ

Проблемы обнаружения и выделения информативных составляющих в составе многокомпонентных сигналов на фоне внешних шумов возникают при решении многих практических задач, связанных с проведением экспериментальных исследований физических свойств объектов в самых различных областях науки и техники. В частности, методы обнаружения и анализа состава сигналов играют существенную роль при решении задач в биомедицинской и экологической инженерии, при обработке телекоммуникационных и акустических сигналов и т. п. Как правило, шумы являются результатом различного рода физических флюктуаций, носят случайный характер и являются аддитивными и некоррелированными. Следует отметить, что спектр шумов может занимать широкую полосу частот и перекрывать спектр информационного сигнала по всему его частотному диапазону. В этих условиях одновременная регистрация с основным информационным сигналом мешающих шумов может привести к его существенному искажению во временнóй области и получению аномальных результатов измерений. По- этому задача надежного обнаружения и восстановления информационного сигнала без существенного искажения его полезных составляющих является актуальной задачей. При этом в качестве критерия оптимальности может служить степень искажения формы (спектрального состава) восстановленного сигнала.

Под обнаружением сигнала понимают констатацию факта его наличия. В случае работы в условиях присутствия внешних шумов задача обнаружения сигнала сводится к принятию решения: имеет ли место информационный сигнал, маскируемый шумом, или присутствует только шум. При положительном ответе возникает задача выделения информационных составляющих сигнала из смеси с шумом и восстановление сигнала. Решение этой задачи состоит в получении сигнала, который был бы наименее отличающимся по своим характеристикам от передаваемого [1, 2].

Ввиду того, что внешние шумы, а во многих случаях и полезный сигнал, носят вероятностный характер, современные подходы к анализу зашумленных непрерывных во времени многокомпонентных сигналов основываются на измерении их частотно-временных характеристик с использова- нием методов статистической обработки. Одними из наиболее эффективных среди этих методов являются методы, направленные на проведение гармонического анализа. В процессе такого анализа осуществляется выделение гармонических компонент на фоне внешнего широкополосного шума.

С математической точки зрения наиболее адекватной формой представления многокомпонентного сигнала являются полигармонические функции, которые описываются суммой гармонических колебаний. Что же касается внешнего шума e(t), то в пределах времени анализа его обычно рассматривают как фоновый с непрерывным спектром, с нулевым математическим ожиданием и постоянной дисперсией σe2 . В соответствии с этим математическая модель центрированного, т. е. имеющего нулевое математическое ожидание, полезного сигнала xo(t) в аддитивном шуме e(t) имеет вид xe (t) = x (t) + e (t) =

K

= Z ( a k cos2 nkf ) t + b k sin2nkf , 1 ) + e ( t ),    (1)

к = 1

где a_k и b_k — коэффициенты ряда Фурье; f ₀ — основная частота гармонических составляющих.

Модель (1) имеет нулевое математическое ожидание. Это является оправданной абстракцией, т. к. постоянная составляющая в наблюдаемом сигнале всегда может быть удалена путем использования операции центрирования. Допущение об отсутствии постоянной составляющей позволяет сосредоточить основное внимание на идентификации непосредственно гармонических составляющих.

С инженерной точки зрения более рациональной формой представления гармонических составляющих является их запись в полярных координатах. В этом случае (1) примет вид

K

o

x e ⁽ t ) = Z “ k co^{S(2n f} k t + Ф к ) + e ( t )• к = 1

В (2) для k -й гармонической составляющей с частотой f_k = kf 0 будут соответствовать амплитуда α_k и начальная фаза ϕ_k :

« k =V a k + b k , Ф k = arctg ( — Mak ) •      ⁽³⁾

Амплитуды α_k образуют амплитудный спектр, а начальные фазы ϕ_k — фазовый спектр.

В соответствии с (1)–(3), уточняя общую задачу гармонического анализа, подчеркнем, что он связан с получением на дискретных частотах f_k = kf 0

оценок a ˆ _k и b ^ˆ _k коэффициентов ряда Фурье и вычислением оценок α ˆ _k амплитудного и ϕ ˆ _k фазового спектров на фоне широкополосного шума e ( t ) . Отметим, что амплитудный и фазовый спектры полигармонического сигнала являются дискретными.

Ввиду явного преимущества на практике для обработки сигналов широко используется цифровой гармонический анализ. Существующие цифровые алгоритмы гармонического анализа, основу которых составляют процедуры быстрого преобразования Фурье, позволяют обеспечить эффективную обработку цифровых отсчетов анализируемого сигнала. Однако в реальных условиях при низких значениях отношения сигнал/шум становится сложно различить полезный сигнал, и малое число разрядов АЦП оказывается недостаточным для точного представления сигналов в широкополосном шуме. Решение данной проблемы за счет простого увеличения числа разрядов АЦП приводит к усложнению процедур цифрового представления и обработки сигналов. При этом выбор числа уровней квантования может быть ограничен, а также может зависеть от разрешающей способности датчиков, регистрирующих сигналы. Таким образом, простое увеличение числа разрядов не может быть абсолютным решением качественного представления сигналов в цифровом виде. Кроме того, при равномерном шаге квантования помехозащищенность от шумов будет разной для полезных сигналов с малой амплитудой и с большой. Относительная погрешность квантования для сильных сигналов будет меньше, в то время как для слабых сигналов она будет больше. В соответствии с этим следует использовать методы первичного преобразования сигналов, обеспечивающие рациональное соотношение между точностью цифрового представления сигналов и простотой технического решения.

ЦИФРОВОЙ АЛГОРИТМ АНАЛИЗА СПЕКТРАЛЬНОГО СОСТАВА И ВЫДЕЛЕНИЕ ГАРМОНИЧЕСКИХ СОСТАВЛЯЮЩИХ МНОГОКОМПОНЕНТНЫХ СИГНАЛОВ

Для повышения эффективности обнаружения компонент информативных сигналов (особенно слабых составляющих) в аддитивной смеси с широкополосным шумом предлагается осуществлять цифровую обработку сигналов на основе знакового аналого-стохастического квантования, которое позволяет осуществлять предельно грубое двухуровневое (бинарное) квантование без систематической погрешности независимо от статистических свойств преобразуемых сигналов [1, 3–5].

Знаковое аналого-стохастическое квантование представляет собой нелинейную операцию веро- ятностного округления реализации непрерывного сигнала, где в качестве меры квантования выступает вспомогательный случайный сигнал ξ(t) . В результате такого квантования получаем ограниченный по уровню знаковый сигнал:

z ( t ) =

+ 1, если

- 1, если

X e ( t ) + £ ( t ) >  0;

X e ( t ) + ^(t ) <  0.

Вспомогательный сигнал ξ(t) принимает значения в пределах от -£max до +^max и имеет равномерное распределение. Здесь £max >| Xe (t) |max, где | xoe(t) |max — максимально возможное по абсолютной величине значение, которое может принять Xe (t) = x(t) + e(t).

Оценки коэффициентов ряда Фурье a ˆ _k и b ^ˆ _k в процессе гармонического анализа в пределах интервала времени t ₀ <  t <  t ₀ + T будем искать в следующем виде [6]:

t0 + T atk = 2-T-1 J z(t)cos(2nkf,t)dt,          (5)

t ₀

t 0 + T bk = 2-T-1 J z(t)sin(2nkf,t)dt ,           (6)

t ₀

где k = 1,2,3,..., K ;      f , = 1/ T ;      cos(2nkf , t )

и sin(2 πkf ₀ t ) — фильтрующие функции.

Величина f , = 1/ T соответствует величине предельного разрешения по частоте дискретных гармонических составляющих.

Обозначим 1 0 = 1 ₀ и t p = 1 ₀ + T . Не нарушая общности и строгости математических рассуждений, будем считать, что 1 ₀ = 0 и, следовательно, t p = T . Пусть множество { t ' } , где 1 <  i <  I - 1 и t^z z = t p , определяет те моменты времени, в которые знаковый сигнал z ( t ) в пределах интервала 0 <  t <  t p меняет текущее значение на противоположное значение. Тогда (5) и (6) можно записать следующим образом:

i - 1 t z + 1

a k = 2^ T ^{- 1} Z J z ( t)cos(2nkf , t )d t ,         (7)

i = 0 _fz t_i

I - 1 t z + 1

b k = 2L T ^{- 1} Z J z ( t )sin(2 nkf , t )d t .         (8)

i=0 ti ti

Знаковый сигнал z ( t ) принимает значения - 1 и + 1, которые чередуются строго последовательно во времени и остаются постоянными в переделах интервалов t p <  t <  t p _{+ 1} . Поэтому достаточно знать только его начальное значение z ( t ₀ ) . Принимая это во внимание, интегралы в (7) и (8) можно проинтегрировать аналитически, и оценки a ˆ _k и b_k примут вид:

i - 1

a k = 2 ^ max ( kn ) ^{- 1} z ( 1 0 ) Z ( - 1) ' ^{- 1} sin(2 nkf , t ' ),     (9)

i = 1

I bk = ^™(kn)-1 z(10)Z(-1)4 cos(2nkf,ti), (10) i=0

[ 1, при i = 0, i = I ;

^i I

[ 2 , при 1 <  i <  I - 1 .

В (9) и (10) перейдем к числовому представлению моментов времени t_i^z . Тогда будем иметь t i = n i A t , где A t — период следования счетных импульсов и i = 1,2,3,..., I - 1. При этом 1 0 = n 0 A t и t p = T = N A t . В соответствии с этим интервалу времени 1 0 <  t <  t p , в пределах которого осуществляется вычисление оценок a ˆ _k и b ^ˆ _k , будет соответствовать его дискретный аналог П 0 A t <  n A t <  n I A t , или просто n 0 <  n <  n I . Кроме того, если 1 ₀ = 0, то n 0 = 0 и n I = N .

Подставив в (9) и (10) числовые оценки моментов времени t_i^z , окончательно получаем

I - 1

a k = 2 ^ max ( kn ) ^{- 1} z ( 1 0 ) Z ( - 1) ' ^{- 1} sin(2nkN - 1 ^ ), (11) i = 1

b ⁷ k = ² ^ nax ^{( kn} )   z ⁽ t 0 ) ^X

X

( 1±h):

I 2

I - 1

+ Z ( - 1) ' cos(2 nkN ^- 1 n , ^z)

i = 1

Из (12) следует, что если I является нечетным, то будем иметь

I - 1

b)_k = 2 ^ max ( kn ) ^{- 1} z ( 1 0 ) Z ( - 1) ' cos(2nkN ^{- 1} n 0 ). i = 1

Таким образом, вычисление оценок коэффициентов ряда Фурье aˆk и bˆk в цифровом виде в конечном итоге свелось к формированию двух матриц размером K x (I -1) с дискретными значениями фильтрующих функций sin(2nkN-xnz) и cos(2nkN-1niz), обработка которых осуществля- ется согласно (11) и (12). При этом важной особенностью такой обработки является то, что основными операциями являются простейшие арифметические операции суммирования и вычитания. Практически она не требует осуществлять операции цифрового умножения.

Для принятия решения об обнаружении гармонических составляющих используется критерий, основу которого составляет принцип превышения оценок амплитуд гармонических составляющих порогового значения. Согласно этому критерию устанавливается уровень значимости гармонических составляющих в зависимости от характера решаемой задачи. Если значение полученной оценки амплитуды α ˆ _k гармонической составляющей с частотой 2 πkIN , где k = 1,2,3,..., K , меньше установленного уровня ε ₀ , то считается, что данная гармоническая составляющая не является значимой, и она не принимается во внимание.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО ЭКСПЕРИМЕНТА

На основе соотношений (11) и (12), а также критерия принятия решения с учетом задания уровня значимости гармонических составляющих разработан цифровой алгоритм обнаружения сигналов на фоне внешних широкополосных шумов. Моделирование практической реализации данного алгоритма проводилось с использованием имита- ционного моделирования процедуры знакового аналого-стохастического квантования.

В процессе формирования модели (2) генерировались гармонические составляющие с нормированными частотами f_k ^н , значения которых изменялись от нуля до 0.5. Амплитуды α_k принимались от нуля до единицы. Начальные фазы ϕ_k задавались с помощью генератора равномерно распределенных величин в пределах - π ≤ ϕ_k ≤ π . Некоррелированный аддитивный шум e ( t ) представлял собой белый шум с нулевым математическим ожиданием и единичной дисперсией. В частности модель (2) содержала одиннадцать гармонических составляющих, параметры которых приведены в таблице. В этой же таблице приведены результаты вычисления оценок α ˆ _k и ϕ ˆ _k , а также представлены значения относительных погрешностей δ_α и δ_ϕ для этих оценок.

На рис. 1 показан вид полезного сигнала x ( t ) , соответствующий набору гармонических составляющих из таблицы. На рис. 2 представлен сигнал x^o e ( t ), определяемый моделью (2). На рис. 3 приведен результат гармонического анализа, представляющий собой нормированную оценку спектра амплитуд α ˆ _k , которые вычислены с разрешением 0.001 единиц нормированной частоты.

o

Параметры гармонических составляющих модели сигнала x ( t ) и их оценки

k	fk н	αk	αk	, % α ,	ϕk , рад	ϕk	δ ϕ , %	αk / σe , дБ
1	0.225	0.1	0.1012	1.20	–1.2961	–1.3226	2.04	–20.00
2	0.23	0.2	0.2008	0.40	1.3905	1.3800	–0.76	–13.98
3	0.235	0.3	0.2980	–0.67	–2.3089	–2.3199	0.48	–10.46
4	0.24	0.4	0.4008	0.20	–1.5957	–1.6012	0.34	–7.96
5	0.245	0.5	0.5021	0.42	–0.6312	–0.6331	0.30	–6.02
6	0.25	1	1.0019	0.19	–0.0833	–0.0857	2.88	0.00
7	0.255	0.5	0.4994	–0.12	–0.6962	–0.7080	1.69	–6.02
8	0.26	0.4	0.4006	0.15	1.3449	1.3486	0.28	–7.96
9	0.265	0.3	0.2970	–1.00	2.6846	2.6777	–0.26	–10.46
10	0.27	0.2	0.1986	–0.70	1.0151	1.0315	1.62	–13.98
11	0.275	0.1	0.1016	1.60	–1.7407	–1.7742	1.92	–20.00

o

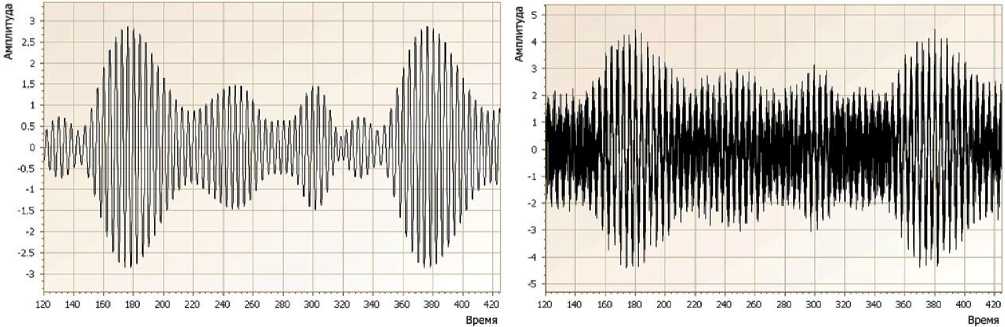
Рис. 1. Модель полезного сигнала x ( t )

o

Рис. 2. Модель сигнала x e ( t )

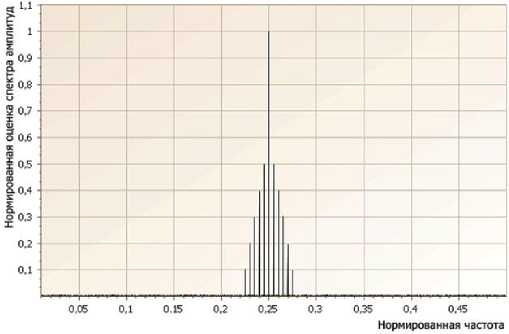
Рис. 3. Нормированная оценка спектра амплитуд α ˆ _k

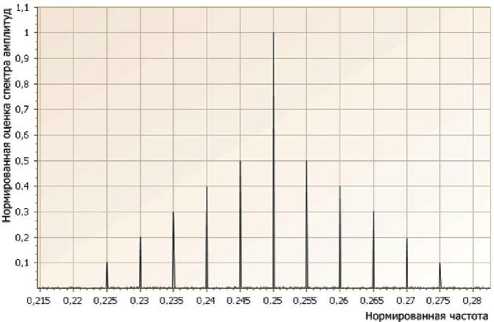
Рис. 4. Нормированная оценка спектра амплитуд α ˆ _k в пределах частотного диапазона, занимаемого гармоническими составляющими сигнала

Для большей наглядности разрешающей способности разработанного алгоритма на рис. 4 представлена нормированная оценка спектра амплитуд αˆk в пределах частотного диапазона, занимаемого гармоническими составляющими полезного сигнала x(t) . На рис. 5 приведена оценка спектра амплитуд αˆk в децибелах. Хорошо видно, что спектральная оценка шума после обработки исходного сигнала xo e(t) остается на достаточно низком уровне (в среднем около -50 дБ) по отношению к оценкам гармонических составляющих. Это свидетельствует о высокой устойчивости разработанного алгоритма к внешним некоррелированным аддитивным шумам. На рис. 6 пред- ставлен вид непрерывного восстановленного во временнόй области сигнала xoв(t) , полученного по оценкам αˆk .

Приведенные результаты моделирования свидетельствуют о том, что положения оценок гармонических составляющих в спектре точно соответствуют табличным данным. Ложных линий в спектре не наблюдается, спектральные линии четко различимы. Они не маскируют друг друга. Значения оценок амплитуд α ˆ _k и начальных фаз ϕ ˆ _k получены с относительными погрешностями, которые не превышают соответственно двух и трех процентов, что позволяет говорить о высокой точности их вычисления в статистическом смысле.

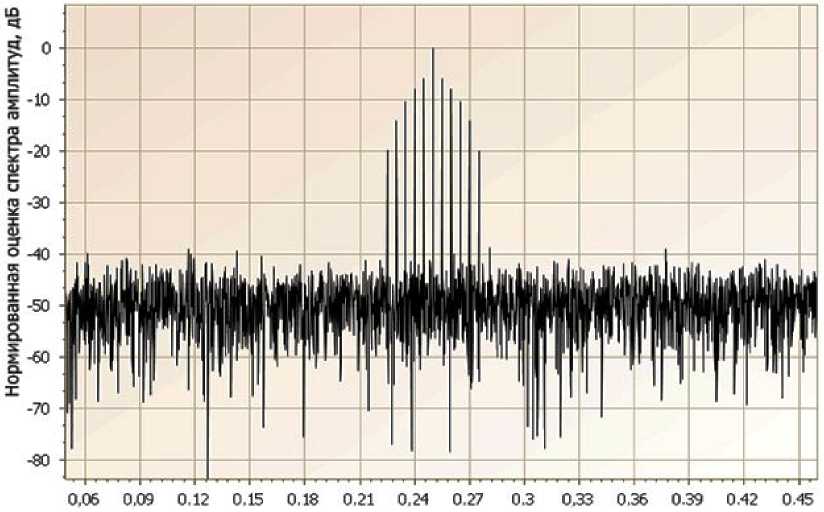
Нормированная частота

Рис. 5. Оценка спектра амплитуд α ˆ _k в децибелах

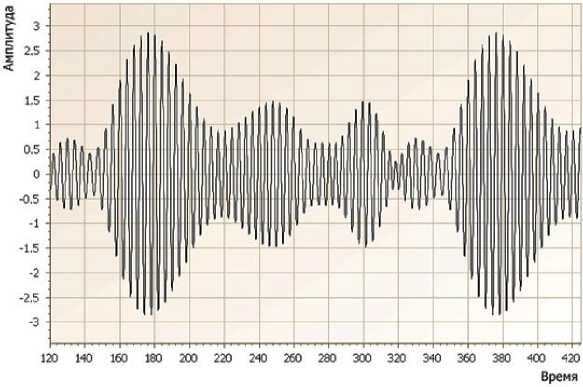
o

Рис. 6. Восстановленный сигнал x в ( t )

ЗАКЛЮЧЕНИЕ

На основе использования знакового аналогостохастического квантования разработан цифровой алгоритм, который достаточно эффективно устраняет влияния внешнего некоррелированного аддитивного шума и позволяет получить высокое качество оценивания спектра гармонических составляющих непрерывных многокомпонентных информационных сигналов. Кроме того, данный алгоритм практически исключает необходимость выполнения многоразрядных операций цифрового умножения, которые свойственны классическому цифровому гармоническому анализу Фурье. Как было отмечено выше, в нашем случае основными операциями являются простейшие арифметические операции суммирования и вычитания дискретных значений фильтрующих функций, соот- ветствующих моментам времени, в которые результат знакового аналого-стохастического квантования меняет свой знак на противоположный. Уменьшение числа операций умножения ведет к сокращению временных затрат, что обеспечивает вычислительную эффективность гармонического анализа.

Работа выполнена при финансовой поддержке РФФИ (проект № 16-08-00269 -А).