Золотое сечение и прогнозирование по авторегрессии
Автор: Городов А.А., Кузнецов А.А., Демьяненко О.В.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Математика и информатика
Статья в выпуске: 2, 2012 года.
Бесплатный доступ
В статье предлагается метод подбора параметров, основанный на использовании числовых рядов в AR( p) моделях. Показана связь прогнозов по авторегрессии с треугольником Паскаля и числами Фибоначчи и Трибоначчи. Даны рекомендации по применению золотого сечения при прогнозировании.
Временные ряды, нормированные числовые ряды, ar(p) модели, ряд фибоначчи, треугольник паскаля
Короткий адрес: https://sciup.org/14082244
IDR: 14082244 | УДК: 519.8
Golden section and forecasting on autoregress
he trial and error method of parameters based on numerical series use in AR( p) models is offered in the article. Connection of the forecasts on autoregress with the Pascal triangle, Fibonacci numbers and Tribonacci numbers is shown. Recommendations on golden section application in the process of forecasting are given.
Текст научной статьи Золотое сечение и прогнозирование по авторегрессии
Если практически все в нашем мире базируется на коэффициентах Фибоначчи, почему бы не использовать их в техническом анализе движения цен на биржах. Впервые это предложил Ральф Нельсон Эллиотт. В дальнейшем будет показано, что данное предположение недалеко от истины.
В практических задачах прогнозирования по временным рядам одним из часто применяемых методов является модель авторегрессии p -го порядка AR( p ). В данной модели текущее значение ряда xt представляется в виде линейной комбинации конечного числа предыдущих значений процесса и случайной величины s t :
xt = Ф1xt-1 + Ф 2xt-2 + ••• + Ф pxt-p + £ t, где ф1, ф 2, •, ф p - весовые коэффициенты [1].
Как правило, нахождение параметров ф 1 , ф 2 , • , ф p осуществляется по методу наименьших квадратов (МНК) и методу максимального правдоподобия (ММП) [2,3].
В работе [4] был предложен метод подбора параметров, основанный на использовании нормированных числовых рядов в AR( p ) моделях. Сделан сравнительный анализ результатов моделирования временных рядов данного метода с другими известными.
и ж
При этом под нормированным понимается сходящийся числовой ряд ^ b i , если ^ b y = 1 .
i = 0 i = 0
Текущее значение ряда xt будет представлено следующим образом:
xt = b0xt-1 + b0xt-2 + • + bp-1 xt-p + St, где b0, b0,..., bp-1 - первые p членов нормированного числового ряда, выступающие в качестве весовых коэффициентов предыстории временного ряда.
Прогнозное значение y t + 1 вычисляется следующим образом:
(m;p) (m;p) (m;p) (m;p)
yt+1 b0 xt + bl xt-1 + •" + bp-1 xt-p+1 , или p-1
y (.,) = ^ Ь . х_ , (1)
i = 0
где m – номер нормированного числового ряда из некоторой базы рядов, обладающих вышеуказанными свойствами; p - порядок модели; верхний индекс ( m;p ) указывает на номер ряда и на порядок модели.
Формула представляет собой модель прогнозирования по полной предыстории (разложение Вольда).
При этом прогнозное значение y tm1p) будет представлять собой сумму предыстории динамического ряда с весовыми коэффициентами, являющимися элементами числового ряда.
В большинстве задач прогнозирования необходимо делать прогноз на k значений вперед из xt . Как указывалось выше, прогноз на одно значение вперед согласно методу нормированных числовых рядов будет рассчитываться по формуле (1).
Несколько упростим формулу (1), тогда p-1
y t + 1 = V bixt - i + 1 . (1а)
i = 0
Согласно (1а) прогноз на k значений вперед из xt :
yt+2 = boyt+1 ' Vb xt , i=1
yt+3 = boyt+2 + b1yt+1 +V bixt-i, i=2
y.x v = b„YtiV + b,yti. , + ••• + У bxt ■ ^
J t+k 0J t+k-1 U t+k-2i t i=k k-2t ytiv = У byti. . + У b x, .. J t+k i^ t+k-ii t i=0i
Далее рассмотрим прогноз в моделях AR(2).
Авторегрессия 2-го порядка
Распишем прогноз при использовании только двух предшествующих членов динамического ряда.
yt+1 = boxt + b1xt-1, yt+2 = boyt+1 + b1xt = b0(b0xt + b1xt-1) + b1xt (b + b1 )xt + b0b1Xt-1, yt+3 = b0yt+2 + b1yt+1 = b0 Kb2 + b1 )xt + b0b1xt-1 ]+ b1 [b0xt + b1xt-1 ] = = (b0+2b0b1 )xt+(b0b1+b 2 K1, yt+4 = b0Y^3 + b1yt+2 = b0 [(b0 + 2b0b1 )xt + (b2b1 + b2 K1 ] + + b1 [(b2 + b1 )x t + b0b1xt-1 ] = (b4 + 3b0b1 + b2 Xt + (b0b1 + 2b0b2 Xt-1 .
Либо можно записать:
Y t + k =a 1 ( k ) xt + « 2 ( k ) xt - 1 .
Выпишем ряд весовых коэффициентов при xt для различных k :
ai (1) = bo a1 (2)=b2+bl
-
a , ( 3 ) = b 0 + 2b o b i
-
a , ( 4 ) = b + 3b 2 b 1 + b 2
a 1 ( 5 ) = b 0 + 4b 0 b 1 + 3bob 2
a1 (6) = b0 + 5b4b1 + 6b0b2 + b a1 (7) = b7 + 6b0b1 + 10b0b2 + 4bob3 a1 (8) = b0 + 7b0b1 + 15b 4b2 + 10b2b3 + b4
a k + ( k__1 ) bk - 2b 1 ( k 2 )( k 3 ) bk - 4b2 -1
a i ( k ) b o + i! b o b i + 21 b o b i +
, . (k^rjfc-r-l)—(k-2r + l)hk-2rbr + . bo bl, r!
где a1 (k) - это весовой коэффициент при xt; k - порядковый номер прогнозного значения; r - целая часть от деления .
Иначе a1 ( k ) можно записать в следующей форме:
-
a , ( k ) = ОД + Cb b + + C k — , b k - 2r b r .
Нетрудно заметить тот факт, что каждый из вертикальных рядов данной последовательности имеет биномиальные коэффициенты возрастающих прогрессий, представляющих собой сечение по основанию треугольника Паскаля (рис.).
1 1
|
12 |
1 |
|
13 |
31 |
|
14 |
641 |
|
15 |
10 10 5 1 |
|
16 |
15 20 15 6 1 |
|
17 |
21 35 35 21 7 1 |
|
18 |
28 56 70 56 28 8 1 |
|
19 |
36 84 126 126 84 36 9 1 |
Треугольник Паскаля
С помощью следующей леммы докажем, что выдвинутое утверждение верно для любого k .
Лемма 1. Пусть a,(k )=од+сод-2ь, +-----+ Ck-rbk 2гЬГ - весовой коэффициент при xt при прогнозировании по МНЧР.
Тогда a,(k +1) = co+bk + ОДЛ + ^ + Ck-r+bo-Mbr.
Доказательство.
1 k 1 k - 1
Отметим, что если к четное то, тогда r = — , в случае к нечетного, тогда r =------ .
-
1. Рассмотрим первый случай при k четном, тогда искомую формулу весового коэффициента при
x t можно записать в следующем виде:
а , ( к ) = С кЛк + C k - , b k - 2 b , + C k - 2 b ; - 4 b 2
k - 1 , k - 1 + - + C k Ш2
-+1 2
kk
+ C k b 2 .
Заметим, что величина
k - 2
нечетная, а в этом случае r = —-— , или
k r =--1. Тогда
, . , k 2 . k i 1 kk-31» i Л',2 i k-5i 2 . . /-<2 k3k2
+ Ck - 2b0 Ь1 + Ck - 3Ь0 Ь1 + + Ck Ь0Ь1
-+ 1 2
k - 1 k - 1
+ C 2 b o b 12 .
При этом количество членов в а 1 (k) на одно больше, чем у а 1 (k - 1) .
Докажем по индукции, что
а 1 ( k + 1 ) = C O + ]b k * 1
, ,, . , , . k -1 , k + С 1bk-1b +С2 bk-3b2 +—ьС2 b3b2 + C k b 0 b 1 + Ck - 1 b 0 b 1 + + Ck + 2 b 0 b 1
kk
+ C 2 bo b 2
—+1
при условии, что k четное.
Пусть формула (2) верна. Тогда
а; ( k + 1 ) = boа1 ( k ) + b1a1 ( k - 1 ) =
= b
k - 1
C k b k + ^-ХЛ + C k - 2 b k - 4 b 2 + - + C 2 b2 b
-+ 1
k - 1
kk
+ C 2 b2
+
+ b 1 C k - 1 b
k - 1
, , , , , „ , г „ k-2 , k k-1 I /~'1 kk-3i . z-12 i k -5i 2 . । 2 k3k2 0 + Ck - 2b0 b1 + Ck - 3b0 b1 + + Ck b0b1
-+ 1 2
- 2
k - 1 k - 1
+ C 2 b o b 2
kk
л i . 1 , . k I . k -1 - - Cobk+1+C1 bk b + C2 b b2+-*- + C2 b3b2 + C2bb2 C k b 0 + Ck - 1 b o b 1 + Ck - 2 b o b 1 + + Ck , 0 b 1 + Ck b 0 b 1
k ,
k - 1
k - 1
+
k
i 0 kk-1k i /'"'1 kk - 3r2 . ^2 L.k-51.3 . . /''<2 k3k2 i 2 К к. 2
+ C k - 1b0 b1 + C k - 2b0 b1 + C k - 3b0 b1 + + Ck b0b1 + Ck b0b1
— +
k-1
C22
kk
-+1
k - 1
b 0 b 2 +
k ° - 1
C 2 + C 2 kk
k bob2.
Используя свойства биномиальных коэффициентов
C s + C s - 1 = C s C 0
n n n + 1 ’ n
Cn + 1
= 1 ,
получим
а 1 ( k + 1 ) = b o a 1 ( k ) + b 1 a 1 ( k - 1 ) =
k 1 k 1 k k
= C0 bk+1+C1bk"1b +C2 bk"3b2+'" + C2- b3b2- + C2 b b2 , C k + 1 b o + C k b 0 b1 + C k - 1 b 0 b1 + + C k , 0 b 1 + C k 1U0U1 ’
-+2 —+ 1
что и требовалось.
2. Рассмотрим второй случай при k нечетном.
Тогда k-3 k-3 k—1 k -1
0k k /'-'1 Kk — 2i Г^2 k — 4i 2 2 3i 2 2 2
a i ( k / = Ckb0 + Ck - 1b0 Ь1 + Ck - 2Ь0 Ь1 ' ' Ck + 3b0 b i + Ck + 1b0b1 .
В этом случае величина ( k — 1 ) четная, тогда r = —-—.
В свою очередь k—3 k—3 k—1 k—1
0 k — 1 /'"'1 Kk — 3k /^2 k —4i 2 2 2 2 2 2
a 1 ( k — 1 ) = Ck — 1Ь0 + Ck — 2Ь0 Ь1 + Ck — 3Ь0 Ь1 + + Ck + 1b0b1 + Ck — 1Ь1
При этом количество членов в a 1 (k) тоже, что и у a 1 (k — 1) .
Докажем по индукции, что k—1 k—1 k+1 k+1
0 hk^+C1 +С2 hk—3b2^2 h2h 2
a 1 ( k + 1 ) C k + 1b0 + C k — 2b0 b1 + C k — 1b0 b1 + + C k + 3b0b1 + C k + 1b1 ’ (3)
при условии, что k нечетное.
Пусть формула (3) верна. Тогда a1 (k +1) = b0a1 (k) + b1a1 (k — 1) =
= b
k — 3 k — 3 k — 1 k — 1
C 0bk + C1 bk—2b +C2 bk—4b2 ч2 b3b 2 + C 2 b b 2
C kb0 + C k — 1b0 b1 + C k - 2U0 b1 + + C k + 3b0b1 + C k + 1b0b1
+
+ b1
k — 3 k — 3 k — 1 k — 1
С0 bk-1+C1 bk—3b + C2 bk 4h22 b2h 2 +CTbT C k - 1b0 + C k — 2b0 b1 + C k — 3b0 b1 + + C k + 1b0b1 + C k — 1b1
k — 3 k — 3 k — 1 k — 1
С0bk+1+C1 bk—1b +С2 bk—3h2+-" + C 2 b4b 2 +C2b2b2
C kb0 + C k — 1b0 b1 + C k — 2b0 b1 + + C k + 3b0b1 + C k + 1b0b1
+
+
k — 3 k — 1 k — 1 k + 1
С0 bk—1b +С1 bk-3b2+С2 bk^b3+ — + C^b2bv+Cvbv C k — 1b0 b1 + C k — 2b0 b1 + C k - 3b0 b1 + + C k + 1b0b1 + C k — 1b1
= c0bk+1 + [c1 +c0 lbk-1b + Гс2 +С1 V v i C kb0 + L C k — 1 + C k — 1 ] b0 b1 + L C k — 2 + C k — 2 ] b0 b1 +
k — 1
k — 3
+
C k + 1 + C k + 1
k—1 k—1k
22 22
b0b1 + Ck—1b1
Воспользуемся уже указанными свойствами биномиальных коэффициентов и C n = C ^ ' 1 = 1 . Получим k — 1 k — 1 k + 1 k + 1
„ । l\ 0 К k + 1 . /~х1 К k — 1 к । /'-'2 Kk—3i 2 . . 2 К 2 К 2 ■ 2 К 2
a 1 ( k + 1 )= C k + 1b0 + C k — 2b0 b1 + C k — 1b0 b1 + + C k + 3b0b1 + Ck + 1b1 *
Из пунктов 1 и 2 следует, что формула верна для любого k . Лемма доказана.
w
Предложение 1. Пусть ^ b 0 - нормированный знакоположительный степенной ряд, где i = 0 w
0i <1, т.е. ^ bi = b0+ b2 + b0 • • • . 1=0
Преобразуем ряд весовых коэффициентов при x t , тогда:
а 1 ( 1 ) = b o « 1 ( 2 ) = 2 b a 1 ( 3 ) = 3b 0 a i W = 5b4 a 1 ( 5 ) = 8b 0 a 1 ( 6 ) = 13b 0
a (k )=f2 (k+i)bk, где F2 (k +1) - ряд чисел Фибоначчи.
Определение 1. Последовательность чисел, начинающаяся с двух единиц F 2 ( 1 ) = F 2 ( 2 ) = 1 , а каждое из следующих получается сложением двух предыдущих, называется рядом Фибоначчи , а члены ее – числами Фибоначчи .
Покажем, что выдвинутое утверждение верно.
W
Лемма 2. Пусть ^ b 0 - нормированный знакоположительный степенной ряд, где 0 < b i <1 . То- i = 0
гда a 1 ( k ) = F 2 ( k + 1 ) b k , где F 2 ( k + 1 ) - ряд чисел Фибоначчи.
Доказательство. Ряд чисел Фибоначчи имеет общую рекурсивную формулу представления:
F 2 ( k + 1 ) = F 2 ( k ) + F 2 ( k - 1 ) .
Тогда a1 (k ) = boa1 (k -1)+b0a1 (k - 2)=bo (F2 (k )bk)+b0 (F2 (k - 1)bk-1 )=
= b k ( F 2 ( k ) + F 2 ( k - 1 )) = F 2 ( k + 1 ) b k .
Лемма доказана.
Докажем, что при увеличении k весовой коэффициент a 1 (k) обнуляется, в случае непревосход-ства b0 величины, обратной золотому сечению.
Лемма 3. Пусть b0<
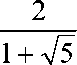
. Тогда lim a. ( k ) = 0 . k ^® 1
Доказательство. Воспользуемся формулой Бине [5]:
F 2 (k ) = IT
1 + 75 1 - Vs где Y1 = 2 , Y 2 = —.
Также произведем замену b0 = — , где q > 1 . Тогда
q
a 1 ( k ) = F 2 ( k + 1 ) ^ .
Определим предел k -го члена:
lim a. ( k ) = lim k ^w k ^x
( k + 1 ) v( k + 1 )
1 -Y 2
1 q k
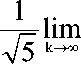
■ ( k + 1 ) v( k + 1 )
1 -Y 2
q k
= -j=lim
V 5 k —v
Y k “ ' 1
—
/ \ (k+1A
Y 2
q k
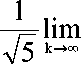
Г
q k
z
Y 1
_^llm Ь
k
l q 7
= 1|*0 = 0,
при q > Y i .
Проверим ряд на сходимость по признаку Коши:
llmk / a.(k) = llm k—v v n 7 k^M
ffl^-y^
k 5q k
= llm k—v
( у (ы| —Y?^ _ 1 rf1 *’ —Y? ± 1 ) ) k
5 k ± 2 q q llm5 k ± 2
= — lim у. k q k —v 1
( k ± 1 ) <
—
уИ k
l
Г
_ -llm YY 1 q i—>v
_1 1 llm у 1
q i ^« 1
b<1 q
при q > Y 1 .
Вернемся к замене, тогда при b0
1 <
Y 1
llm a, ( 1 ) _ 0 . Лемма доказана. k —v 1 v 7
Теперь рассмотрим ряд весовых коэффициентов при x t — 1 для различных 1 : a 2 ( 1 )= Ь1
a 2 ( 2 ) = Ь0Ь1
a 2 ( 3 ) _ b 2 b1 + b 2
a 2 ( 4 )_ b0 b 1 ± 2bob2
a 2 ( 5 ) _ b^ + 3b 2 b 2 + b 3
a 2 ( 6 ) _ b 0 b1 + 4b 3 0b 2 + 3b0b 3
a 2 ( 7 ) _ b 0 b1 + 5b 0 b 2 + 6b 2 b 3 + ь ;
a b1Ъ __2)b1—3b2 I ( 1 3 )( 1 4 ) b1—5b3
a 2 ( 1 ) b 0 b 1 ± 1! b 0 b 1 ± 2! b 0 b 1 ±
( k — r-l ) ( k-r-2 ) — ( k-2r ) 1 — 2r ± 1
± b0 b1 , r!
где a 2 ( k ) - это весовой коэффициент при xt — 1 ; k - порядковый номер прогнозного значения; r -
1 — 1
целая часть от деления .
Запишем a 2 ( k ) в следующей форме:
a 2 ( 1 ) _ C k b ' b + C k — 2 b 0 — 3 b 2 + ^ + C ' b' ' b" .
Поэтому была сформулирована следующая лемма, доказательство ее аналогично лемме 1.
Лемма 4. Пусть a 2 (k) _ Ck—1bk—1b1 + Ck-2b1-3b2 +-----+ Ck-rb^2rbr+1 - весовой коэффици- ент при xt при прогнозировании по МНЧР.
Тогда a2(k +1) = Ckb;b1 + Ck-1bk-2b,2 + ■ + C b b ' b'+2 Доказательство.
Как и в лемме 2 приведем доказательство для k -четного и нечетного.
1 k - 1
1. Пусть k -четное, тогда . В свою очередь:
a2 (k) = c. Ь'Ъ + CJ'- b + "
k - 2 k
+ Ck - 2U0bl ’
Величины ( k - 1 ) и ( k + 1 ) нечетные:
kk a2(k -1)=Ck-2b.k-2bl + Ck b' bb + ■ + Clb2.
Докажем по индукции, что:
k + 2 k + 2
a 2 ( k + 1 ) = ОД! + C k - 1 b kk - 2 b 2 + ■ + CyV ,
.
при условии, что k четное.
Пусть формула (4) верна. Тогда
a 2 (k +1) = b0a 2 (k) + b1a 2 (k -1) = k-2 k
= b C0 bk-1b + C1 bk-3b b2 + — + C 2 b b2
b o Ck-1 b 0 b 1 + Ck-2 b 0 b 0 b 1 + + Ck-2 b 0 b 1
k - 1
k - 2
k - 2
+
kk
+ b C0 bk-2b + C1 bk-4b2+ — + C2b2 + b 1 Ck - 2 b 0 b 1 + Ck - 3 b 0 b 1 + + Ck b 1
k - 2
k - 3
k
_ 2 _ k-2 k
C k - 1 b k b 1 + CLXbb + ■ + CZ 2 b 2 b 2
2 k k+2 "
i 0 к k-2к 2 . p1 Lk-4k3 । । r'lk 2
+ Ck - 2b0 b1 + Ck - 3b0 b1 + + Ckb1
k - 2
k - 3
+
0k1
Ck - 1U0U1 + LCk - 2
“ k - 2 k
.+ г 2 +C2
+ C k + 2 + Ck + 2
k k k + 2 bb F + C 2 b 12 .
Воспользуемся уже указанными свойствами биноминальных коэффициентов. Получим k + 2 k + 2
a 2 ( k + 1 ) = C 0 b 0 b . + C . b - 2 b 2 + ■ + C , , b . ,
что и требовалось.
k - 1
2. Пусть k нечетное, тогда r =----- . В свою очередь:
a 2 ( k ) = C b k' b + CJb b +
k - 1 k - 1
+ Ck + 1 b 1 .
Величины ( k - 1 ) и ( k + 1 ) нечетные:
a2 (k -1) = C b b + Ckb' 4b + ■ k-3 k-3
+ C k + 1 b 0 b 1 .
Докажем по индукции, что k+1 k-1
a 2 ( k + 1 ) = C k b 0 b i + CLb k - 2ь 2 + - + e£b o b ,“
при условии, что k четное.
Пусть формула (5) верна. Тогда
a 2 (k +1) = b0a 2 (k) + b1 a 2 (k -1) =
= b
k - 1 k - 1
C0 bk-1b + C1 I? V +C 2 b 2 Ck - 1 b 0 b1 + Ck - 2 b 0 b1 + + Ck + 1 b 1
+
+ b1
k - 3 k - 3
C0 bk-2b + C1 bk-4b2 + - - - + C 2 b b 2
Ck - 2 b 0 b1 + Ck - 3 b 0 b1 + + Ck + 1 b 0 b 1
k - 1 k - 1
C 0 LkL । Г^1 Lk-2i42 . । 2 L к 2
k - 1b0b1 + Ck - 2b0 b1 + + Ck + 1b0b1
+
+
k - 3 k - 1
C k - 2 b k - 2 b 2 + C k - 3 b k - 4 b 3 + - + C k +AK
= C0 bkb + fc1 + C0 lbk-1b2 + • • Ck-1b0b1 + LCk-2 + Ck-2_IU0 b1 +
k - 1 k - 3
22 + Ck + 1 + Ck + 1
_ 2 2
k - 1 b 0 b 12 .
Воспользуемся уже указанными свойствами биноминальных коэффициентов. Получим k + 1 k - 1
a 2 ( k + 1 ) = C^b . + C k - 1 b kk - 2 b 2 + - + c . „b b - .
Лемма доказана для любого k .
Используя предложение 1, преобразуем a 2 ( k ) , получим:
a 2 ( 1 ) = b0
a 2 ( 2 ) = b0
a 2 ( 3 ) = 2b 4
a 2 ( 4 ) = 3b 0
a 2 ( 5 ) = 5b 0
a 2 ( k ) = F 2 ( k ) b k + 1 , где F2 ( k ) – ряд чисел Фибоначчи.
«
Лемма 5. Пусть ^ b 0 - нормированный знакоположительный степенной ряд, где 0 < b i <1 . То- i = 0
гда a 2 ( k ) = F 2 ( k ) b k + 1 , где F 2 ( k ) – ряд чисел Фибоначчи.
Доказательство. Пусть лемма 5 верна. Тогда a 2 (k )=Ka 2 (k -1)+b0a 2 (k - 2)=60 (F2 (k - 1)b0)+b2 (F (k - 2)b )= = Ь0*' (F (k -1)+ F2 (k - 2)) = F2 (k )b0+1.
Лемма доказана.
Нетрудно доказать, что a 2 ( k ) ч 0 при k > x .
Как и в случае с a 1 (k) , при достаточно большом k коэффициент a 2(k) будет зависеть от золотого сечения.
Лемма 6. Пусть b0<
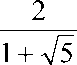
. Тогда lim ajk ) = 0 .
k —V 2 V 2
Доказательство.
Произведем аналогичную замену b0 = — , где q > 1 . q
Тогда vk lim a 2 (k )= lim — k—v k—v _
-
Y *j
5 q ( k + 1 ) 5qq
Y ( 1 lim — k —v
-
Ak 1
(Y 1
V * 1 / у
qk
5 q
lim k — v
k
Y- к q J
= 0
при q > y i .
Проверим ряд на сходимость по признаку Коши:
lim k I a, ( k ) = lim k —v v 2X7 k —v
i lim^ -y k ) k
q lim5 k + 2 q k k ^w
Y k
—
Y k
k
V v5qk '
= lim
= -lim Yj 1 q k ^ v
—
к
5 k + 2 qq k
:k) k
= *<1 q
при q > Y i .
< — lim a 2 ( k ) = 0 . Теорема доказана. л/ k— —v
/ 1
Вернемся к замене, тогда при b0
Если из данного ряда коэффициентов a 2 ( k ) вынести b1 за скобки, мы получим: a 2 ( k ) = b1 a 1 ( k - 1 ) .
С помощью следующей леммы докажем данное утверждение.
Лемма 7. Пусть a 1 ( k ) - это весовой коэффициент при x t , a 2 ( k ) - это весовой коэффициент при x t - 1 при прогнозировании в AR ( 2 ) по МНЧР. Тогда a 2 ( k ) = b1 a 1 ( k — 1 ) .
Доказательство. Согласно лемме 2:
a 1 ( k — 1 ) = F 2 ( k ) b 0 — 1
Согласно лемме 5:
a 2 ( k ) = F 2 ( k K' = F 2 ( k F b 2 = F 2 ( k ) b k — 1 b 1 = b 1 a 1 ( k — 1 ) .
Лемма доказана.
Поэтому a 2 ( k ) имеет те же свойства, что a 1 ( k ) .
Обобщим вышесказанное.
Теорема 1. Пусть yt+k = a1 (k )xt + a 2 (k )xt—1 - прогнозная модель AR(2) по МНЧР. Тогда спра- ведливы следующие утверждения:
-
1) a 1 ( k ) = F 2 ( k + 1 ) b k ;
-
2) a 2 ( k ) = F 2 ( k ) b k + 1 ;
-
3) a 2 ( k ) = b1 a 1 ( k — 1 ) ;
4) limy t + k = 0 при b 0 <
1 + 55
5) limy t + k k ^x
1 1 + V5
6) limy t + k =x при b0 > k ^x
xt + ;----^x t - 1 при b0 =
5 5 1 + y5
;
1 + Д
1 + V5
.
Доказательство. Первое утверждение доказывается леммой 2. Второе леммой 5. Третье утверждение на основе леммы 7.
Доказательство четвертого утверждения доказывается на основе лемм 3 и 6:
limy t + k = lim ( a 1 ( k ) xt + a 2 ( k ) xt - 1 ) = lim a 1 ( k ) xt + lim a 2 ( k ) x k ^x k ^x v k ^x k ^x
t - 1
= x, lim a, ( k ) + x,_, lim a, ( k ) = 0 * xt + 0 * x t k ^x 1 ' 7 t 1 k ^x 2 ' 7 t
t - 1
= 0.
На основе 3 и 6 леммы доказывается 5 и 6 пункт теоремы:
lim a. ( k ) = , lim a, ( k ) = -U—, при b„ = y,.
k ^“ 1 v 7 55 k ^“ 2 v 7 55 у 0
lim y,x. = x, lim a. ( k ) + x,, lim a, ( k ) = Д —- x, k ., t + k t k ., i' 1 k .. 2х t
+17;—^xt - 1.
lim a 1 ( k ) = x , lim a 2 ( k ) = x , при b0 > у 1 .
limyt + k = x t lim a 1 ( k ) + xt - 1 lim a 2 ( k ) = x • x k ^w k ^x k ^x
t
+ «• xt - 1 =x .
Теорема доказана.
Данная теорема позволяет сделать вывод о том, что любой прогноз в модели AR(2) – это распределение предыстории в будущем через золотое сечение.
Далее рассмотрим авторегрессию более высоких порядков.
Авторегрессия 3-го порядка
Распишем прогноз при использовании трех предшествующих членов динамического ряда: y t + k =a 1 ( k ) xt +a 2 ( k ) xt - 1 +a 3 ( k ) xt - 2 .
Используя предложение 1, представим коэффициенты a 1 ( k ) при xt :
a 1 ( 1 )= b.
-
a , ( 2 ) = 2b 2
-
a , ( 3 ) = 4b 0
a . ( 4 ) = 7b 4
a 1 ( 5 ) = 13b 5
« 1 ( k ) = F 3 ( k + 1 ) b ,‘ ,
где F3 ( k + 1 ) – ряд чисел Трибоначчи.
Напомним.
Определение 2. Ряд Трибоначчи – это последовательность чисел, заданная рекурсией F , ( k + 1 ) = F , ( k ) + F , ( k - 1 ) + F 3 ( k - 2 ) , где F , ( 0 ) = 0 , F , ( 1 ) = 1 , F , ( 2 ) = 1 , F , ( 3 ) = 2 .
Был сформулирован и доказан ряд утверждений.
-
w
Лемма 8. Пусть ^ b 0 - нормированный знакоположительный степенной ряд, где 0 < b i <1 . То- i = 0
гда a 1 ( k ) = F 3 ( k + 1 ) b k , где F3 ( k ) - ряд чисел Трибоначчи.
Доказательство. Воспользуемся математической индукцией. Тогда
a1 (k) = b0a1 (k -1)+b 2a1 (k - 2)+b0a1 (k - 3) =
= b 0 ( F 3 ( k ) b 0 - 1 ) + b 0 ( F 3 ( k - l i b ' ■ ) + b 0 ( F 3 ( k - 2 1 b ' ) =
= b ' ( F 3 ( k ) + F 3 ( k - 1 ) + F 3 ( k - 2 )) = F 2 ( k + 1 ) b ' .
Лемма доказана.
ч. Тогда, lim a, ( k ) = 0 . k ^w 1
Лемма 9. Пусть b0<
( 19 + 3233 ) 3 + ( 19 - 3233 ) 3 + 1
Доказательство. Ряд Трибоначчи, помимо рекурсии, можно выразить через функцию:
F3 (k ) =
z
3P - (11 +12 + 1)
к 3
k
в2 - 2P + 4
,
где p = 3/ 586 + 102733 , к , = 3/ 19 + 3733 , 1 2 = 37 19 - 3733 .
Произведем аналогичную замену b 0 = — , где q > 1 .
q
Определим предел k -го члена:
lim a. ( k ) = lim F ( k + 1 ) b k = lim k ^x 1 X 7 k 4x 3 X 70 k 4x
f 1 z
3P - (1. +12 + 1) к 3
\
(1 Ak + 1
3p 1 (1. +12 + 1)к 3____________7в2 - 2p + 4
k
•--------- q k
в2 - 2в + 4
- lim k^w
_ (11 +12 + 1) к 3
2 q k
.
limk/a, ( k ) = limk/F ( k + 1 ) b k = lim k >/ v k >/ v 3 k >/
< 1 z
3p - (11 +12 + 1) k 3
\ k+1
в2 - 2P + 4
•
1 qk
1 k
’P(X, +12 + 1)1 k
= lim
k>»L в2 - 2P + 4 _
( 1 z
T (11 +^ 2 k3
k
A k
k qk
3 (11 +^ 2 + 1)
q
.
Также возможны 3 варианта:
-
1) lim a 1 ( k ) < 1 при q> -( 1 1 +1 2 + 1 ) ;
k >' 3
-
2) lim a 1 ( k ) = 1 при q = -( 1 1 +1 2 + 1 ) ;
k >' 3
-
3) lim a , ( k ) >1 при q< ^( 1 1 +1 2 + 1 ) .
, lim a, ( k ) = 0 . Лемма доказана. k >® 1 V 7
Вернемся к замене, тогда при b0<
(11 + 12 + 1)
Представим коэффициенты a 2 ( k ) при xt - 1 :
a 2 ( 1 ) = b0 a 2 ( 2 ) = 2b 2 a 2 ( 3 ) = 3b 0 a 2 W = 6b4 a 2 ( 5 ) = 11b 0
a 2 (k )= R(k + 1)bok“, где F3 (k +1) - модифицированный ряд чисел Трибоначчи.
Определение 3. Модифицированный ряд Трибоначчи – это последовательность чисел, заданная рекурсией F3 ' ( k + 1 ) = F3 ‘ ( k ) + F3 ‘ ( k - 1 ) + F 3 ( k - 2 ) , где F3 ( 0 ) = 0 , F3 ( 1 ) = 0 , F3 ( 2 ) = 1 , F 3 ( 3 ) = 2 .
«
Лемма 10. Пусть ^ Ь 0 - нормированный знакоположительный степенной ряд, где 0 < b i <1 . То- i = 0
гда a 2 ( k ) = F3 ‘ ( k + 1 ) b k + 1 , где F3 ‘ ( k + 1 ) - модифицированный ряд чисел Трибоначчи.
Доказательство. Аналогично лемме 8:
a 2 (k) = b0a 2 (k -1)+b2a 2 (k - 2)+b0a 2 (k - 3) == b0(F(k>;)+ b0(FJ(k- kb')+ b (ПК -2)bk-2)=
= b ' ( F 3 ' ( k ) + R( k - 1 ) + F; ( k - 2 )) = R( k + 1K ' .
Лемма доказана.
Лемма 11. Пусть b0<
( 19 + 3^33 ) 3 + ( 19 - 3x33 f + 1
й . Тогда, lim ajk ) = 0 .
k ^« 2 V 7
Доказательство. Заметим, что числа модифицированного ряда Трибоначчи, начиная с 3, будут всегда меньше чисел обычного ряда Трибоначчи, поэтому в доказательстве будем использовать функцию из леммы 9.
Произведем аналогичную замену b0 = — , где q > 1 . q
Определим предел k -го члена:
lim a. ( k ) = lim F ( k + 1 ) b k + 1 k ^» 1 V ' k ^® 34 70
3 в 1 (\ + X 2 +13
= lim —-—-------— в2 - 2p + 4
•
q k + 1
3 в в 2 - 2 в + 4
(1 3k + 1
3 (\ +z 2+ 1)
Um -—>1——
3 в в 2 - 2 в + 4
lim k ^»
3 (\ + X 2 + 1)
k + 1
q
В данной ситуации возможны 3 случая:
1) lim a 1 ( k ) = 0 , при q > -( X 1 +X 2 + 1 ) ;
k “3
-
2) lim a 1 ( k ) = k ^»
-
3) lim a.( k ) = k ^» 1 ' '
3P
—-----------, при q = — IX. + X, + 1 ) ;
в2 -2в + 4 3V 127
® , при q < j (X 1 +X 2 + 1 ) .
Проверим ряд на сходимость по признаку Коши:
lim k a ( k ) = lim k/ F ( k + 1 ) b k + 1 = lim k ^w 1X2 k ^w 3 0 k ^w
3 pf 1 ( X , + X 2 + 1 )
- 3
x k + 1
1 k
= lim k^w
в ( X 1 +X 2 + 1 ) 1 k ( в 2 - 2 P + 4 ) q _
k 1 k - ( X 1 +X 2 + 1 ) - 3 ____________ 7
k q k
в 2 - 2 в + 4
3 (X1 +X 2 + 1) q
•
q k + 1
Также возможны 3 варианта:
-
1) lim a 1 ( k ) <1 при q> ^( X 1 +X 2 + 1 ) ;
-
2) lim a 1 ( k ) = 1 при q = ~( X 1 +X 2 + 1 ) ;
-
3) lim a 1 ( k ) >1 при q< ^( X 1 + X 2 + 1 ) .
lim a, ( k ) = 0 . Лемма доказана. k ^» 1
Вернемся к замене, тогда при b0<
(X1 + X 2 +1)
Представим коэффициенты a 3 ( k ) при xt - 2 :
a 3 ( 1 ) = b0 a 3 ( 2 ) = b0 a з ( 3 ) = 2b 0 a 3 ( 4 ) = 4b4 a 3 ( 5 ) = 7b 0
«3 (k )=F3 (k )bk+2, где F3 (k) – ряд чисел Трибоначчи. ®
Лемма 12. Пусть ^ b 0 - нормированный знакоположительный степенной ряд, где 0 < b i < 1 .
i = 0
Тогда a 3 ( k ) = F3 ( k ) b k + 2 , где F3 ( k ) – ряд чисел Трибоначчи.
Доказательство. Аналогично лемме 8 и 9:
a 3 (k) = b0a 3 (k -1) + b0 a 3 (k - 2) + b0a 3 (k - 3) =
= b 0fa ( k - 1 ) b 0 + l ) + b ( F 3 ( k - 2 l b ' ) + b ( F 3 ( k - 3 ) b ' ) =
= b 0 + 2 ( F 3 ( k - 1 ) + F 3 ( k - 2 ) + F 3 ( k - 3 )) = F 3 ( k ) b k".
Лемма доказана.
Лемма 13. Пусть b0<
—=г. Тогда, lim a, ( k ) = 0 .
k ^» 33 '
+ 1
Доказательство.
Произведем аналогичную замену b0 = — , где q > 1 .
q
Определим предел k -го члена:
lim a 3 ( k ) = limF3 ( k ) b k + 2 k ^® k ^®
= lim k^®
<1,
3p - (X, + k 2 +1) k 3;
k
J
P2 - 2p + 4
•------------- qk+2
3P r
= / .— ---vim
(P2 - 2P + 4) ■ •
У 1 z л
, (21 +2 2 + 1) 37
q
k
1 q2
= -- 3P— П lim
( P 2 - 2 P + 4 ) q2 * •*
В данной ситуации возможны 3 случая:
1) lim a 1 ( k ) = 0 , при q > -( 2 1 +2 2 + 1 ) ; k •' 3
2 1 +2 2 + 1
3q _
.
2) lim a 1 ( k ) = k ^w
27P
(P2 - 2P + 4X^1 +X2 +1)2
, при q = j( 2 1 +2 2 + 1 ) ;
-
3) lim a 1 ( k ) = w , при q < - ( 2 1 +2 2 + 1 ) .
k •' 3
Проверим ряд на сходимость по признаку Коши:
lim kMk ) = Um k/ FWbF
= lim
( 1 z
3P - (21 +22 +1) k 3
k
1 k
P 2
—
22P + 4
•
q k * 2
= lim k ^w
3P
1 k
_p2 - 2P + 4_
< 1 z
- (21 +2 2 + 1)
k 3 7
k + 2
q k
k k
3 (21 + 2 2 + 1) q
.
-
2 ) lim a 1 ( k ) = k ^w
< 1 z
3p - (11 +12 +1) к 3
A
в2 - 2в + 4
-, при q =
-
3 (\ +Z 2 + 1 ) ;
Также возможны 3 варианта:
-
1) lim a 1 ( k ) <1 при q> -( 2 1 +2 2 + 1 ) ;
k •' 3
-
2) lim a 1 ( k ) = 1 при q = ~( 2 1 +2 2 + 1 ) ;
-
3) lim a 1 ( k ) >1 при q< ^( 2 1 +2 2 + 1 ) .
lim a. ( k ) = 0 . Лемма доказана. k ^w 1
Вернемся к замене, тогда при b0<
(21 + 2 2 +1)
Лемма 14. Пусть a 1 ( k ) - это весовой коэффициент при x t , a 3 ( k ) - это весовой коэффициент при xt - 2 при прогнозировании в AR ( 3 ) по МНЧР. Тогда a 3 ( k ) = b 0 a 1 ( k — 1 ) .
Доказательство. Согласно лемме 8:
a , ( k - 1 ) = F 3 ( k ) b k - 1 .
Согласно лемме 10:
а з ( к ) = F , ( к >Г = F , ( k ) b 0 b = b 0 a i ( k - 1 ) .
Лемма доказана.
Поэтому a 3 ( к ) имеет те же свойства, что a 1 ( к ) .
Обобщим вышесказанное.
Теорема 2. Пусть yt + k = a 1 ( к ) xt +a 2 ( к ) xt - 1 +a 3 ( к ) xt - 2 - прогнозная модель AR(3) по
МНЧР. Тогда справедливы следующие утверждения:
-
1) a i ( к ) = F , ( к + 1 ) b 0 ;
-
2) a 2 ( к ) = F^k + 1 ) b 0 + 1 ;
-
3) a з (k ) = F, (k F"
-
4) a 3 ( k ) = b0 a 1 ( k - 1 ) ;
-
5) limy t + k к ^w
= 0 , при b0< p
+ 1
-
6) limy t + k k ^w
= C , при b0 =
( 19 + 3Т33 ) 3 + ( 19 - 3Л3 У3 + 1
;
-
7) limy t + k k ^w
= w , при b0 > p
+ 1
.
-
Доказательство. Первое утверждение доказывается леммой 8. Второе леммой 10. Третье утверждение на основе леммы 12. Четвертое – леммой 14.
Доказательство пятого утверждения доказывается на основе лемм 9, 11 и 13:
lim yt+k = lim(a1 (k)xt + a2 (k)xt-1 + a3 (k)xt-2 ) = k^w k^w
= lim a. ( k ) xf + lim ajk ) xf, + lim ajk ) x к X 1 V / t k ^w 2 V 7 t - 1 k ^w 3 V 7
t - 2
= xt lim a 1 ( k ) + xt - 1 lim a 2 ( k ) + xt - 2 lim a 3 ( k ) = k ^w k ^w k ^w
= 0 * xt + 0 * xt - 1 + 0 * xt - 2 = 0.
На основе тех же лемм доказываются 6 и 7 пункты теоремы:
lim ajk ) = k^w 37 7
lim y t + k = x t lim a 1 ( k ) + x t - 1 lim a 2 ( k ) + x t - 1 k ^w k ^w k ^w
эр 3p 27P
x
x + x + t-2
P 2 - 2 P + 4 t p 2 - 2 P + 4 t - 1 ( p 2 - 2 P + 4^ +Z 2 + 1 ) 2
limy t + k = xt lim a 1 ( k ) + xt - 1 lim a 2 ( k ) + xt - 2 lim a 3 ( k ) = k ^w k ^w k ^w k ^w
= w • xt + w • xt-1 + w • xt-2 = w.
Теорема доказана.
Из теоремы следует, что в ряде случаев прогноз в моделях AR(3) есть средневзвешенное последних трех значений динамического ряда с весами золотого сечения.
Заключение. При рассмотрении свойств прогнозов в AR(2) и AR(3) моделях на основе МЧР была выявлена взаимосвязь будущих значений с золотым сечением.
В дальнейшем планируется рассмотреть авторегрессии более высоких порядков и выявить возможные закономерности прогнозов в этих моделях.
