Золотое сечение в математике

Что такое золотое сечение? Однозначного ответа на данный вопрос без выяснений дать невозможно, но тем не менее оно окутало целый мир: население Земли, природу, науку, искусство и даже космос, взяв за основу «золотое число». Записать его практически невозможно, потому что оно состоит из бесконечного ряда цифр, но учёные используют первые 3 числа, что никогда не меняют периодичности-1,61.

Подойдя к этому числу с геометрической стороны за пример можно взять прямоугольник, одна сторона которого в 1,61 раз длиннее другой. Такая фигура называется «золотым прямоугольником». Отсекая от него квадраты можно получить все меньшие «золотые» прямоугольники, соединяя вершины получается линия называемая логарифмической спиралью.

Из последних выводов можно разобраться в взаимоотношении золотого сечения и спиралевидной системы: путем наложения меньших фигур друг на друга, а в последствии соединяя их получается спираль схожая с формами панциря улитки (Рис.1) или со спиралью лепестков распустившейся розы.

Рисунок 1. Форма панциря улитки

Гением, что объединил геометрию, искусство и арифметику является Леонардо Пизанский – Фибоначчи, (один из самых выдающихся математиков). Познакомившись с индо-арабской системой счисления ему удалось понять её преобладание над римскими цифрами.

Фибоначчи написал «Книгу Абака» посвященную теории чисел и содержащую алгебраические задачи. Одна из его задач известна сегодня как последовательность Фибоначчи и формируется следующим образом «Сколько пар кроликов будет у нас через год, если в январе у нас была одна пара, которая каждый месяц производит на свет другую пару, начиная с марта пара, в свою очередь, производит собственное потомство каждый месяц, начиная со второго месяца». Решая её, можно заметить, что каждое число является суммой двух предыдущих, а уравнивая их получаем последовательные члены последовательности Фибоначчи.

Эта последовательность также используется в теореме Пифагора, но мало кому известно, что благодаря числам Фибоначчи нам лишь нужно находить общую площадь квадратов, построенных на катетах прямоугольного треугольника, равную площади квадрата, построенного на гипотенузе. В случае равенства получаем прямоугольный треугольник, если квадрат длины большей стороны превосходит, то треугольник тупоугольный, при большей сумме квадратов треугольник является остроугольным.

В понятии золотого сечения, также присутствует «золотой треугольник», такое призвание дано ему не из-за сторон, увеличивавшихся на 1,61, а из-за сторон с углами 36 и 72 гр. Проверить это достаточно просто: при построении стороны треугольника равны стороне правильного десятиугольника, вписанного в круг, и радиусу этого круга.

Таким образом символ пятиконечной звезды (рис.2) также основан на построении «золотых» треугольников и прямоугольников.

Рисунок 2. Символ пятиконечной звезды.

Знаменитый художник Леонардо Да Винчи соединил науку и анатомию создав иллюстрацию из наблюдений римского механика и архитектора Витрувия. Он доказывал, что рост человека равен размаху рук (рис.3), и если лёжа на спине развести в стороны руки и ноги, то фигура будет вписана в окружность. А сама иллюстрация, по количеству линий, соответствует числам из последовательности Фибоначчи.

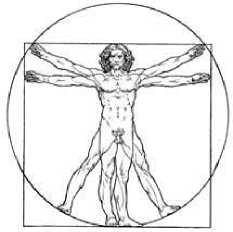
Рисунок 3. Виртувианский человек.

Но не только в строении тела человека присутствует «божественная» гармония сечения и чисел, но и даже в ДНК человека. Молекула ДНК состоит из двух вертикально переплетенных спиралей, длина каждой из них в развернутом виде составляет 34, а ширина 21. Эти числа чередуются в последовательности Фибоначчи и соотносятся как 1,61.

Значит, что же такое – золотое сечение? Это наша с вами жизнь. Млечный путь, цветение, животный мир – всему есть логическое объяснение, скрытое в числах и теоремах. И музыка, и картины, и наука: всё принадлежит «Божественной пропорции», что установила соотношения, соблюдающиеся для достижения красоты, как отражение математики.