Зоны безопасности резонанса ферменной конструкции с произвольным числом панелей

• 1    Введение / Introductions

Объектом настоящего исследования является новая схема статически определимой регулярной фермы. Цель исследования — вывод аналитический зависимости первой частоты собственных колебаний конструкции от числа панелей, размеров фермы ее массы и жесткости.

Частота собственных колебаний конструкции существенно зависит от ее размеров и характера распределения масс. Для обеспечения безопасной работы конструкции знание области, в которой нет собственных частот системы произвольного порядка, имеет большое значение. Размер этой области зависит от размеров конструкции, распределения масс и жесткости. Проблема определения резонансной области безопасности фермы недостаточно изучена [1], [2]. В настоящей работе на примере плоской статически определимой регулярной фермы изучается проблема зависимости области резонансной безопасности от размеров конструкции. Решение представлено графиком, как результат численного анализа на основе аналитического решения задачи о спектре собственных частот свободных колебаний фермы.

Отдельная задача — определение аналитической зависимости первой частоты фермы от размеров панелей и их числа. Метод конечных элементов [3]–[5] является наиболее распространенной в инженерной практике математической моделью определения собственной частоты колебаний фермы. На практике инженера интересует, как правило, только верхняя и нижняя оценки первой частоты фермы. Известны приближенные численные метод Донкерлея [6]–[9] и метод Luong, C.L.

Resonance safety zones of a truss structure with an arbitrary number of panels;

Рэлея [10]–[12]. Метод Рэлея зачастую обладает высокой точностью, однако коэффициенты, получаемые этим методом, часто бывают довольно громоздкими, особенно для сложных конструкций, для которых вывести общую расчетную формулу сложно или невозможно. В данной работе для определения первой частоты колебаний фермы предложен метод Донкерлея и его упрощенный вариант [13], [14]. Формулы для коэффициентов, полученные методом упрощения, значительно компактней, чем по методу Донкерлея и при этом дают результаты с более высокой точностью. В данной работе система линейных уравнений для расчета усилий в стержнях фермы решается в символьном виде [15]–[17] с помощью специальных операторов в программе компьютерной математики Maple для произвольного числа панелей. Общие вопросы существования решений для статически определимых регулярных структур рассматривали Hutchinson R.G. и Fleck N.A. [18], [19]. Нелинейная параметрическая вибрация панелей переменной толщины изучалась в [20].

• 2    Материалы и методы / Materials and Methods

  2.1    Конструкция фермы

Рассматриваемая ферма представляет собой плоскую балочную конструкцию с ромбовидной решеткой и двумя опорами (рис. 1). Одна опора подвижная, другая – неподвижная шарнирная. Длина пролета фермы L = a (4 n + 4) . Вся масса фермы равномерно распределена по K = 4 n + 13 узлам конструкции, за исключением двух опорных узлов. Ферма содержит v = 8 n + 20 стержней. В это число также входят три стержня, моделирующие опоры. Для определения сил в стержнях используется программа на языке Maple, позволяющая находить силы в стержнях в аналитическом виде.

Рис. 1 - Ферма, n = 3

Fig. 1 - Truss, n = 3

Нумерация стержней и узлов дана на рисунке 2. Вводится специальный упорядоченный список номеров вершин концов соответствующих стержней. Фрагмент программы, который импортирует координаты в систему Maple, имеет вид:

• >    x[1]:=0:y[1]:=0:

• >    x[2]:=a:y[2]:=0:

• >    for i to 2*n+1 do x[i+2]:=2*a*i:y[i+2]:=h: end:

• >    L0:=4a*(n+1):

• >    x[2*n+4]:=L0-a: y[2*n+4]:=0:

• >    x[2*n+5]:=L0: y[2*n+5]:=0:

• >    x[2*n+6]:=0: y[2*n+6]:=h:

• >    x[4*n+10]:=L0: y[4*n+10]:=h:

• >    for i to 2*n+3 do x[i+2*n+6]:=2*a*(i-1):y[i+2*n+6]:=3*h: end:

• >    x[m3-2]:=0:     y[m3-2]:=-h:

• >    x[m3-1 ]:=L0:    y[m3-1]:=-h:

• >    x[m3]:=L0+a:   y[m3]:=0:

  

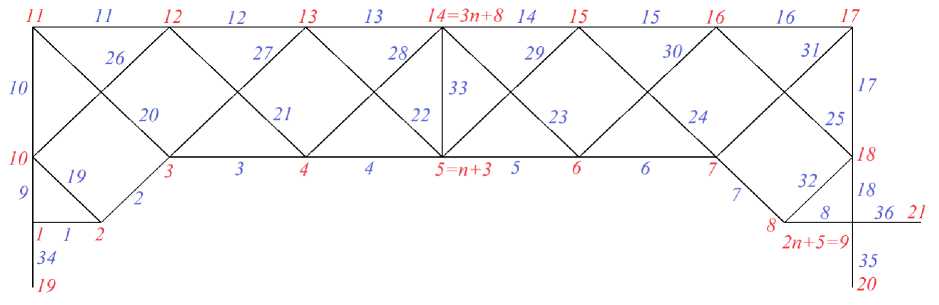
  Рис. 2 - Нумерация стержней и узлов, n = 2

  Fig. 2 - Numbering of bars and nodes, n = 2

  
  
2.2    Расчет усилий в стержнях 2.3    Расчет прогиба

Решение системы линейных уравнений в системе Maple с помощью стандартных операторов дает аналитические выражения для всех усилий. Дополнительно операторы Maple позволяют получить наглядную картину распределения сил в стержнях в численном режиме данной программы. При n = 2 , a = 3 м , h = 1 м , на рисунке 3 представлено численное решение задачи распределения усилий по стержням фермы. Величина модуля силы пропорциональна толщине стержней, элемент сжатия показан синим цветом, элемент растяжения — красным, а несжатый элемент — черным.

Рис. 3 - Распределение усилий, нагрузка по всему поясу, n = 2

Fig. 3 - Distribution of forces, load across the entire belt, n = 2

С помощью формулы Максвелла – Мора рассчитывают прогиб фермы:

v - 3

4= 1 S iP ⁾ S i" l i/ ( EF ), i = 1

где S iP ) - усилие в стержне i от действия нагрузки, S ® - усилие от единичной вертикальной силы, приложенной к узлу C , в котором вычисляется прогиб, E и F – модуль упругости и площадь сечения стержней, l _i – длина стержня.

Реакции трех опор не входят в сумму (1), поскольку предполагается, что они недеформируемые. С применением операторов Maple прогиб плоской рамы с нагруженным верхним поясом дает следующий результат:

Aj = P (70 a ³ + 10 c ³ + 21 h ³) / (2 h ² EF ), Д₂ = P (344 a ³ + 60 c ³ + 43 h ³) / (2 h ² EF ), A₃ = P (862 a ³ + 50 c ³ + 33 h ³)/(2 h ² EF ), Д₄ = P (1952 a ³ + 128 c ³ + 63 h ³) / (2 h ² EF ), Д₅ = P (3654 a ³ + 114 c ³ + 45 h ³)/(2 h ² EF ),...

Здесь c = 7 h ² + a² . Общая формула зависимости прогиба от количества панелей и размеров конструкции выглядит следующим образом:

Д„ = P ( C_xa ³ + C₂c ³ + C₃h ³) / ( h ² EF ),                                  (2)

где

C = (10 n ⁴ + 40 n ³ + 20 n ² - 40 n + 15 - 24( - 1) ⁿ n - 27( - 1) ⁿ ) /12, C ₂ = (6 n ² + 12 n - 3 - 8( - 1) ⁿ n - 9( - 1) ⁿ ) / 4,

C ₃ = (8 n + 11 - 2( - 1) n n - 2( - 1) n )/2.

Аналогично при загрузке нижнего пояса плоской рамы получаем следующие коэффициенты: C = (10 n ⁴ + 40 n ³ + 32 n ² - 40 n - 39 + 24( - 1) n ^{+ 1} + 27( - 1) n ) /12,

C ₂ = (6 n ² + 4 n - 5 + 8( - 1) n ⁽ n ^{+ 1)} + 9( - 1) n ) / 4, C = (8 n + 3 - 2( - 1) ⁿn + 2( - 1) n )/2.

Рис. 4 – Зависимость прогиб фермы от количества панелей

Fig. 4 – Dependence of truss deflection on the number of panels

В рассматриваемой ферме при распределении нагрузки по верхнему поясу полученное решение для безразмерного прогиба представлено в зависимости от числа панелей для Д’ имеет следующую форму:

Д'=Д k EF /( P^L ),                                 (3)

где фиксирована суммарная нагрузка P_sum = (2 n + 3) P и длина пролета L = 4 a (n + 1) = 30 м .

Когда число панелей в ферме не слишком велико, можно прогнозировать зависимость прогиба от количества панелей на разной высоте h : из графика на рис. 4 видно, что прогиб пропорционален высоте, т.е. чем выше высота, тем больше прогиб.

2.4    Метод Донкерлея для определения первой частоты собственных колебаний фермы

Нижняя оценка частоты первого колебания по методу Донкерлея [21], [22] имеет следующий вид:

K

• - ■ = M S S p = M A n . p = 1

  
  

По результатам расчета в программе Maple видно, что вид коэффициента A _n не зависит от значения n и имеет следующую формулу n :

,    143 a ³ + 84 c ³ + 97 h ³

A, =                         ,

• ¹        4 h ² EF

  ^A 2

  
  

  ^A 3

  
  

  A 4

  
  

  ^A 5

  
  

  2675 a ³ + 879 c ³ + 952 h³

  18h 2 EF

  6822 a ³ +1422 c ³ +1081 h³

  16h 2 EF

  49425 a ³ + 7045 c ³ + 4112 h³

  50h2EF

  23863 a ³ + 2459 c ³ +1163 h³

  12h2EF

  
  

Здесь обозначены длины раскосов: c = a а² + h ² операторов позволяет получить общую формулу A _n :

В Maple использование специальных

A _n = ( Ca ³ + C₂c ³ + C₃h ³)/( h ² EF ),                             (5)

Решая рекуррентные уравнения, получаются следующие коэффициенты:

128 n ⁵ + 640 n ⁴ + 1660 n ³ + 2360 n ² + 1422 n + 225

92( n + 1)

12 n ³ + 32 n ² + 130 n + 9

2( n + 1)          ^,

44 n ³+159 n ²+ 184 n + 72

3( n + 1)²            .

Для рассматриваемой фермы по полученным коэффициентам формулу оценки первой частоты колебаний фермы можно смоделировать следующим образом:

^ D

= h

EF

M ( C 1 a ³ + C ₂ c ³ + C ₃ h ³ )

2.5 Вариант метода Донкерлея

В [23]–[25] представлена упрощенная формула метода Донкерлея для получения аналитической зависимости первой частоты колебаний от числа панелей. Соответственно, формула расчета имеет вид:

K

• й *² = ^ u p = Ku* /2 . р = 1

  
  

Здесь u* — максимальный парциальный прогиб некоторого узла фермы от действия на ферму единичной силы, приложенной к этому узлу.

Рис. 5 - Зависимость парциального прогиба u_p от номера узла фермы при n = 2

Fig. 5 - Partial deflection dependence u_p on the node number of the truss at n = 2

В исследуемой ферме при разных значениях n , u * достигает максимального значения в

среднем узле верхнего пояса с номером 3 n + 8 . Вычисление величины % = %_и+8 для различных

порядков фермы дает следующую последовательность:

n = 1 : % =

42 c ³ + 14 c ³ + 14 h³ h²EF

n = 2 : U% n = 3 : U% n = 4 : % n = 5 : %

171 a ³ + 27 c ³ + 36 h³

h ² EF       ’

484 a ³ + 44 c ³ + 22 h³

h ² EF        ’

1105 a ³ + 65 c ³ + 52 h³

h ² EF

2190 a ³ + 90 c ³ + 30 h³

h2EF

При произвольном количестве панелей n общая формула принимает следующий вид

C 1 = (2 n + 5)( n + 1)(2 n ² + 4 n + 3)/3,

C ₂ = (2 n + 5)( n + 1) ,

C з = (2 n + 5)((- 1) n + 3) .

Используя операторы программы Maple, формула (7) для оценки первой частоты фермы с полученными коэффициентами приобретает следующий вид:

(% = 2 h

I                          3 EF

M (2 n + 5)(( n + 1)(2 n ² + 4 n + 3) a ³ + 3( n + 1) c ³ + 3(( - 1) ⁿ + 3) h ³) '

• 3    Результаты и обсуждение / Results and Discussion

  3.1    Численное решение

С использованием численного решения для первой частоты, найденной из всего спектра собственных частот колебаний фермы, можно оценить точность предложенных методов. Предположим, ферма в анализируемом примере имеет размеры a = 3м, h = 2м. Площади 2

поперечного сечения стержней решетки и опорных стержней равны: F = 4см . Модуль упругости стали E = 2.1 ' 10⁵ МПа, масса в узлах M = 100кг . На рисунке 6 кривыми показана зависимость первой частоты фермы от количества панелей. На рисунке зеленая кривая w — это результат, полученный численным методом. Кривая w_D соответствует методу Донкерлея, а кривая w * — упрощенному методу.

Рис. 6 – Зависимость первой частоты от количества панелей фермы

Fig. 6 – Dependence of the first frequency on the number of farm panels

Из графиков видно, что первая частота фермы, полученная предложенными методами, монотонно уменьшается и быстро сходится к численному решению по мере увеличения числа панелей. Результаты, полученные методами упрощенным и Донкерлея, не сильно отклоняются от численного метода. Это показывает, что оба метода, предложенные в анализируемом примере, дают Luong, C.L.

Resonance safety zones of a truss structure with an arbitrary number of panels;

хорошие результаты и подходят для оценки первой частоты при большом количестве рассматриваемых панелей фермы. Рассчитывая относительные погрешности &_D= ( о, о,, )/ о, и £. = | ю₁ - и. | / ®,, можно уточнить погрешность решений. На рисунке 7 показана погрешность двух предложенных методов для разного значения высоты фермы.

Рис. 7 – Относительные погрешности методов, высота h в метрах

Fig. 7 – Relative errors of methods, height h in meters

Из рисунка 7 видно, что для метода Донкерлея погрешность не превышает значения 30%. При достаточно больших размерах фермы, а именно при n >  4 , погрешность составляет менее 20%, что является вполне приемлемым уровнем для данного метода. На самом деле для ферм с небольшим количеством панелей это не имеет большого практического смысла. Для упрощенного метода полученные результаты значительно лучше, чем для метода Донкерлея, особенно при n >  4 значение погрешность всегда меньше 10%. Отсюда можно сделать вывод, что для ферм с большим количеством панелей упрощенный метод показывает гораздо большую пригодность и эффективность, чем метод Донкерлея.

3.2    Зависимость безопасного диапазона частоты от размера фермы

Для более точной оценки динамики и оптимизации конструкции необходимо учитывать зависимость размера зоны безопасности по возникновению резонанса от размера конструкции. Для этого необходимо сначала рассмотреть спектры собственных частот регулярных ферм. В зависимости от типа конструкции и конкретных характеристик фермы спектры собственных частот может быть различным. По характеристикам частотных спектров можно оценить динамические характеристики фермы. Спектр собственных частот представляет собой совокупность дискретных величин, соответствующих частотам собственных колебаний, возникающих в ферме под действием возмущающих внешних сил. Резонансная частота может быть определена с помощью этих спектров, что помогает практикующим инженерам лучше понимать динамику фермы и принимать конструкторские решения по характеристикам проектируемой конструкции. На рисунке 8 показан частотный спектр 12 ферм в порядке, соответствующем количеству панелей n = 1,...,12 .

В анализируемом примере, если предположить, что стержни фермы имеют размеры a = 3 м , h = 1 м , на графике рисунка 8 появляются три горизонтальных линии, соединяющих точки, представляющие практически постоянные значения (с незначительными погрешностями)

собственной частоты колебаний для фермы разных порядков. Эти числовые линии обозначены A, B и C соответственно и являются спектральными константами фермы.

Рис. 8 – Спектры регулярных ферм и спектральные константы A, B, C при a = 3 м , h = 1 м

Fig. 8 – Spectra of regular trusses and spectral constants A, B, C; a = 3m, h = 1m

Спектральные константы можно использовать для анализа и оптимизации ферм с большим количеством панелей. На основе расчетных данных и свойств, полученных для ферм с небольшим количеством панелей, эти константы позволяют аппроксимировать собственную частоту колебаний ферм больших порядков. Это имеет значение при оптимизации конструкции фермы с учетом различных требований к жесткости и прочности ее элементов. На рисунке 8 отмечены границы двух областей, в которых нет собственных частот фермы. Такие области называются зонами резонансной безопасности. Информация о зонах резонансной безопасности необходима при анализе реакции конструкции на внешние воздействия. Возмущения с частотой из этой зоны не приводят к резонансу и не окажут негативного (часто катастрофического) воздействия на конструкцию. Знание этих зон имеет большое значение в обеспечении безопасности и долговечности фермы. Зависимость резонансной зоны безопасности от высоты h фермы представлена на рисунке 9.

Рис. 9 – Зависимость безопасного диапазона частот ∆ , ∆от h

Fig. 9 – Dependence of safe frequency range ∆ , ∆ on h

Горизонтальная ось — значение высоты фермы h , вертикальная ось — величина резонансной зоны безопасности. Синяя кривая соответствует области резонанса между спектральными константами A и B , а красная кривая — между B и C . Из рисунка 9 можно сделать вывод, что для рассматриваемой фермы с увеличением высоты фермы h размер зоны резонансной безопасности уменьшается.

• 4    Выводы/ Conclusions

Спектры собственных частот фермы и зависимость размера зоны резонансной безопасности от высоты фермы показаны графически на примере расчета собственных частот статически определенной плоской фермы. С применением метода Донкерлея и его упрощенной формулы найдена зависимость первой собственной частоты колебаний фермы от количества панелей в аналитическом виде. Оба метода пригодны для решения задач ферм с большим количеством панелей. По полученным результатам можно сделать следующие выводы:

• 1    Точность метода Донкерлея и его упрощенного варианта возрастает по мере увеличения числа панелей фермы.

• 2    В рассматриваемом примере формула расчета первой частоты, полученная упрощенным методом, дает большую точность, чем метод Донкерлея.

• 3    Найдены три спектральные константы задачи и две зоны резонансной безопасности.

• 4    Показано, что с увеличением высоты фермы размер зоны резонансной безопасности уменьшается.