Зоны захвата и осаждения капель воды при обтекании цилиндра

Провода высоковольтных линий электропередач (ЛЭП) при соответствующих погодных условиях подвергаются обледенению. На рис. 1 показана фотография ЛЭП с обледеневшими проводами.

Похожие проблемы встречаются в мостовых конструкциях, элементами которых являются тросы. Многократное утяжеление проводов ЛЭП или тросов мостов за счёт обледенения при сопровождающемся возрастании амплитуды колебаний может приводить к обрыву проводов ЛЭП или разрушению тросов мостов и как, следствие, к катастрофическим последствиям в обоих случаях.

Другим примером практической значимости проблемы, рассмотренной в данной статье, является взаимодействие атмосферной влаги с поверхностью летательного аппарата (ЛА). Во время полёта в облаках, содержащих водные капли, их осаждение на поверхности ЛА может приводить к образованию водной плёнки или для переохлаждённых капель к обледенению поверхности ЛА. Если образование водной плёнки на поверхности ЛА может даже в некоторых случаях улучшить аэродинамические характеристики, то обледенение с точки зрения безопасности полёта является вредным явлением, приводящим к срыву потока и, как следствие, к ухудшению аэродинамических характеристик ЛА.

В работе предлагается математическая мо-

Рис. 1. Фото обледенения проводов ЛЭП дель расчёта коэффициента захвата и зоны осаждения водных капель на поверхности круглого цилиндра. Вопросы осаждения водных капель на поверхность цилиндра рассматривались в работах [1-6]. На современном этапе развития компьютерной техники представляет интерес пересчёт коэффициентов захвата с целью уточнения их значений для различных условий движения водных капель.

На рис. 2 показана геометрическая схема траекторий водных капель в потоке воздуха вблизи цилиндра. Капля воды вдали от цилиндра двигается приблизительно по траекториям, совпадающим с линиями тока воздушного потока. Вблизи цилиндра скорости воздушного потока существенно изменяются, а в силу действия на каплю воды массовых и поверхностных сил, её траектория начинает постепенно отклоняться от линии тока и капля может упасть на поверхность цилиндра. Крайние касательные к траектории капли определяют так называемый коэффициент

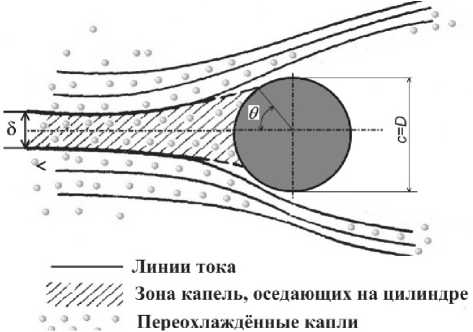
Рис. 2. Линии тока и траектории капель воды вблизи цилиндра

/ Р , = ( V , - , ) р ( Re ₀ ) ; Р , ' = ( V , -, '}( P R Re 0 ) ,

где , = x(L , , = y^L - безразмерные координаты капли; V , , V , - безразмерные местные скорости течения около обтекаемого тела; , , , ' , , , ," – первые и вторые производные от безразмерных координат по безразмерному времени т = tV „ / L , т.е. времени необходимого для того, чтобы капля прошла расстояние L со скоростью V „ (здесь t — размерное время, с ; V „ - скорость набегающего потока, м/c ; L – характерный размер обтекаемого тела (в нашем случае диаметр цилиндра D , м ); безразмерный параметр P определяется формулой

захвата , физический смысл которого является отношение действительного количества воды, осевшего на теле, к тому количеству воды, которое содержится в объёме воздуха, проходимого телом в единицу времени.

Коэффициент захвата определяется формулой [2, 3]

E = 3

c

P = 2 _ r2 V Pw

9   PaL ’ где r - радиус капли, м; pw - плотность водной капли, кг/м3; pa - динамическая вязкость воздуха, Н·с/м2. В системе дифференциальных уравнений (1) функция р(Re0) является безразмерной функцией числа Рейнольдса Re0 = 2rVro/va ( va - кинематическая вязкость воздуха, м2/с), которая имеет вид [2]

где 3 - толщина зоны на бесконечности в невозмущённом потоке между крайними касательными к траекториям капель данного размера, осаждающимися на поверхности тела (см. рис. 2); c – толщина обтекаемого тела (для цилиндра – это его диаметр D ). Зона, простилающая от бесконечности до поверхности цилиндра, и ограниченная двумя предельными траекториями капель данного размера, осаждающимися на поверхность цилиндра (рис. 2, заштрихованная область) называется зоной захвата . На рис. 2 половина зоны осаждения капель на цилиндрической

поверхности показана полярным углом 6 . Ясно, что полуугол, характеризующий зону осаждения, лежит в диапазоне 0 <  6 <  л) 2 рад ( 0 <  6 <  90 ° ) . Расчёт коэффициента захвата и зоны осаждения водных капель на теле сводится к вычислению траекторий капель, которые сталкиваются с этим телом. Их траектории можно получить из решения дифференциальных уравнений движения капель около тела.

Будем полагать, что на каплю действует только одна сила сопротивления (силами веса капли, взаимодействия капли и цилиндра и силами взаимодействия между соседними каплями будем пренебрегать), среду, в которой совершает движение капля, будем полагать несжимаемой идеальной жидкостью. Тогда, используя формулу И.П. Мазина [2] для силы сопротивления можно для плоского случая записать дифференциальные уравнения движения капли в виде [2]

P(Re0) = 1 + 0,17Re23 [(,- V,)2 + (,- V,)2 .

Из системы (1) следует, что траектории капель определяются двумя параметрами P и Re ₀ . Число Рейнольдса Re ₀ служит мерой отклонения от закона Стокса поверхностных вязкостных сил, действующих на каплю. Вместо второго параметра Re ₀ иногда применяют параметр р = Re₀/ Р [2, 3], который является удобным, поскольку не зависит от размера капель.

Используя численные аналоги первых и вторых производных можно систему (1) представить следующим образом:

,.

А т х

^{2 -} "TPi^{( Re} 0 ^{) , - 1}

( А т ) 2

⁺— Р- р , ^{( Re} 0 ⁾ V , ;

, + =

_ А т х

^{2 -} ~р“ P i ( ^Re 0 ) , <

( А т ) 2 , х

⁺ — Р- P i ^{( Re} 0 ^{) V} , ,

Ат , х „ — р , ( ^Re 0 ) 6 - 1 ⁺

, А т        х

^{1 -} ^ P i ^{( Re} 0 ⁾ , i - 1 ⁺

где дискретный аналог функции р(Re0) есть pi (Re0) = 1 + 0,17 (Re0 / Ат)2/3 х х [(V,Ат - , + ,-1 )2 + (V,Ат - , + ,-, )2 ] .

а А т - шаг по безразмерному времени.

Результаты расчёта, показанные ниже, полу-

чены для явной дискретной схемы конечных разностей (2). Исследовалось влияние расстояния

от цилиндра для начала интегрирования и вели чины шага интегрирования на коэффициент зах вата. Расчёты показали, что относительное ми

-

-

-

нимальное расстояние от цилиндра X _min D , равное 15 диаметрам обеспечивает достаточную высокую точность. На рис. 3 для разных значений параметра P показано влияние начального расстояния от цилиндра X _min D на величину коэффициента захвата E. Расчёты также показа-

высокую точность можно выбрать равным ^т = 10 ^ 6 . Сравнение полученных результатов для величины коэффициента захвата от параметра P с результатами других авторов для случая ф = Re ₀ = 0 представлено на рис. 4. На рис. 5 приведено сравнение расчётных данных для угла q , характеризующего зону осаждения (см. рис. 2) от безразмерного параметра P для случая ф = 50000 .

Выполненные расчёты и приведённые сравнения результатов с данными других авторов

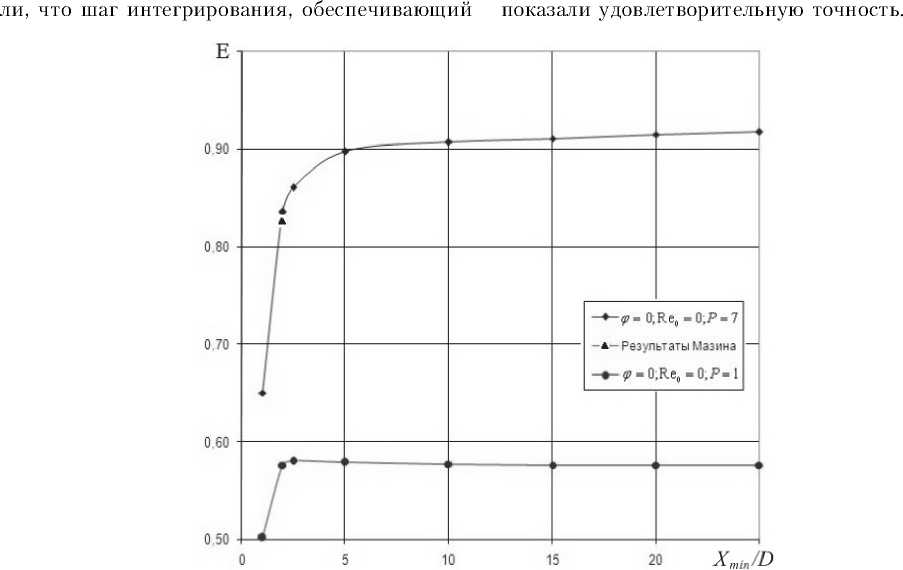
Рис. 3. Влияние относительного начального расстояния от цилиндра при интегрировании на величину коэффициента захвата

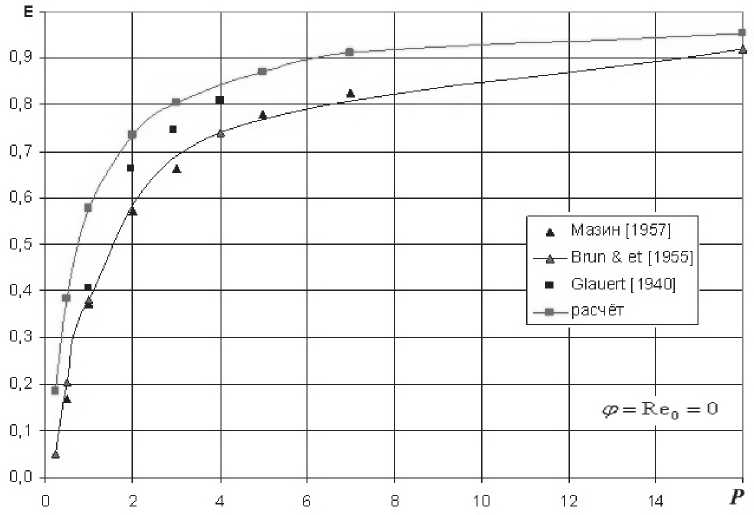
Рис. 4. Зависимость коэффициента захвата от безразмерного параметра P

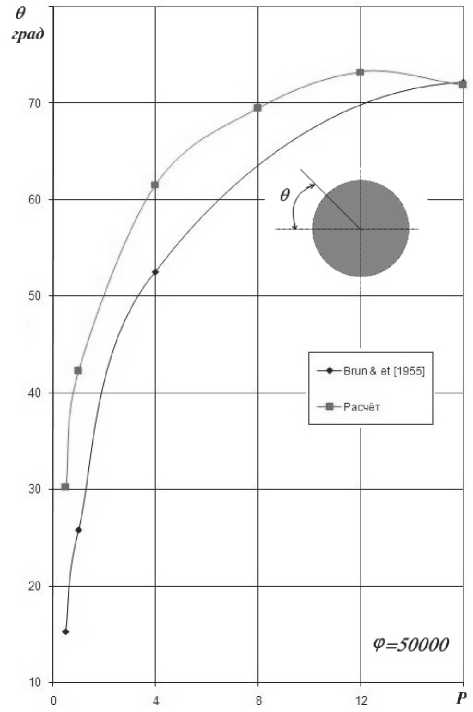
Рис. 5. Зависимость угловой координаты зоны осаждения от безразмерного параметра P

Наблюдаемое небольшое расхождение следует отнести к более грубому шагу интегрирования в работах [1-3], поскольку расчёты проводились на компьютерах того времени. Так в работе

• [1]    расчёты были выполнены на аналоговой вычислительной машине 50-х годов прошлого века. По этой причине можно считать, что расчёты авторов являются более точными.

Дальнейшие развитие математической модели для исследования зон захвата и осаждения будут включать следующие вопросы:

• 1)    учёт сил тяжести и взаимодействия капли с цилиндром;

• 2)    изменение формы поперечного сечения цилиндра в процессе обледенения;

• 3)    учёт сжимаемости;

• 4)    использование современных модификаций закона Стокса для сопротивления капли.