Зубчатые двухступенчатые редукторы. Выбор оптимальной схемы

Основной задачей при проектировании зубчатых редукторов является разработка конструктивных условий формирования параметров ступеней и передаточного отношения каждой ступени. Разбивка общего передаточного отношения редуктора зависит от требований, которые предъявляются к данной конструкции.

Критериями оптимизации наиболее часто выступают стоимость конструкции, минимальные габаритные размеры, минимальная масса, минимальный приведенный момент инерции редуктора, минимальная кинематическая погрешность редуктора.

Рассмотрим методику определения оптимальных параметров коническо-цилиндрического редуктора (рис. 1). Основным условием работоспособности редуктора является условие контактной прочности колес, которое одновременно предусматривает минимальную массу. По-

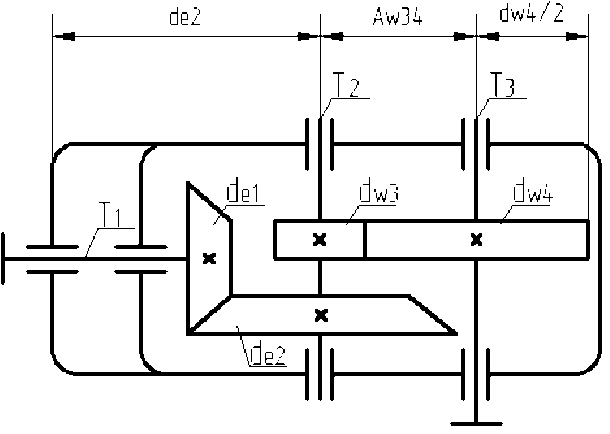
Рис. 1. Схема коническо-цилиндрического редуктора (обозначения см. в тексте)

этому металлоемкость и стоимость редуктора будут зависеть от габаритных размеров редуктора: длины L , высоты H и ширины B .

Необходимо учитывать, что на величину оптимального передаточного отношения ступени оказывают непосредственное влияние такие параметры, как коэффициент ширины зубчатого венца цилиндрической передачи v ba , коэффициент ширины зубчатого венца конической передачи v _bRe , контактное напряжение колес [ а н ]. Поэтому выбор достаточно обоснованных значений пара-

Эта зависимость показывает, что длина редуктора зависит от разбивки передаточного отношения по ступеням и минимальная длина редуктора L _min будет при

а , + а, 12

i 34

a ₂

.

Таким образом, на величину оптимальной разбивки

метров коническо-цилиндрических редукторов является довольно сложной задачей.

Длина коническо-цилиндрического редуктора (см. рис. 1) определяется по зависимости

^L = d e 2 ^{+ A}w 34 ⁺ "у" ,                ⁽¹⁾

где d_{e 2} – внешний делительный диаметр колеса конической передачи; A_{w 34} – межосевое расстояние цилиндрической передачи; d_{w 4} – диаметр делительной окружности колеса цилиндрической передачи.

По условию контактной прочности зубчатых колес

передаточного отношения оказывают влияние соотношение S _а и параметры v _bа и V _bRe . При изменении ширины колес и материалов каждый раз меняются передаточные отношения ступеней и, следовательно, длина редуктора. Оценить это влияние можно с помощью разработанной авторами программы «Система автоматизированного проектирования электромеханического привода. Проектирование коническо-цилиндрического редуктора с оптимальными параметрами САПР-9» (рис. 2).

межосевое расстояние цилиндрической передачи A_{w 34} и внешний делительный диаметр колеса конической пере-

дачи d_{e 2} определяются по следующим формулам:

A

3 нβ34

I W 34 = K a ( i . + 1) 3      ,

V v ba [ ^а н J 34 ■ i 34

где K_а – коэффициент, зависящий от свойств материала и типа передачи; T 3 - момент на валу Т 3 ; K н_р34 - коэффици-

ент неравномерности распределения нагрузки по шири-

не венца цилиндрической передачи; i ₃₄ – передаточное отношение цилиндрической передачи; v _ba - коэффициент ширины зубчатого венца по межосевому расстоянию цилиндрической передачи; [ а _н]₃₄ - допускаемое контактное напряжение колеса цилиндрической передачи;

d _e2

d

т К ■ i

^T 2 ^K нβ12 ⁱ 12

V V bRe [ ^а „ l^¹ - ^0,5 ■V bRe ) 2 ’

где K_d – коэффициент, учитывающий тип передачи и свойства материала; T , - момент на валу Т 2 ; K н_{р 12} - коэффици-

ент неравномерности распределения нагрузки по шири-

не венца конической передачи; i ₁₂ – передаточное отношение конической передачи; v _bRe - коэффициент ширины зубчатого венца конической передачи; [ а _н]₁₂ - допускаемое контактное напряжение колеса конической передачи.

Введем следующее обозначение для соотношений

колес ступеней:

S

^[ ° н L . ^[ ° н L '

С учетом принятых обозначений и формул выражение

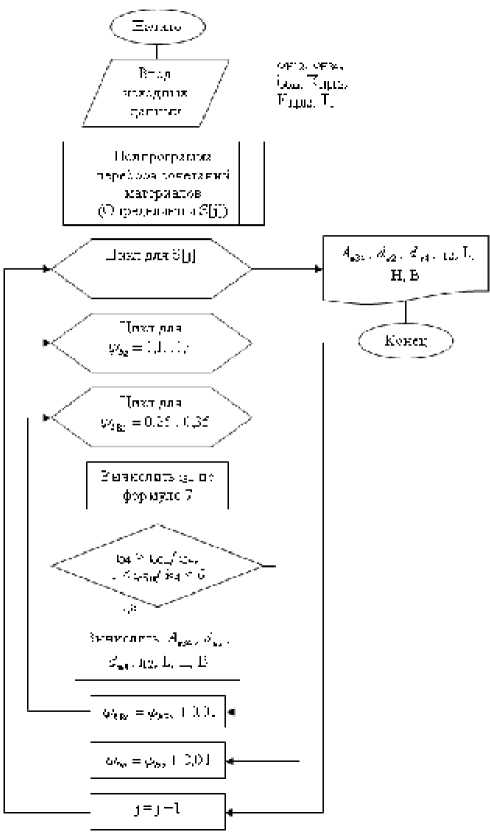
Рис. 2. Алгоритм программы

(1) после соответствующих преобразований примет вид

L = а ₀

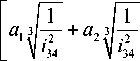
^а 1 = K d 3,

где а о = з

T ■ i общ ■ Л |2 [ а н 1 24

^1Х н ₽ 12 'общ

V bRe ■ ^ _а²(1 - 0,5 ■ V bRe ) 2

3 / K н р 34 ■ Л 34 ψ ba

Вводятся следующие параметры:

• –    массив материалов для колес с различными допускаемыми контактными напряжениями;

• –    общее передаточное отношение редуктора i _общ;

• –    коэффициенты неравномерности распределения нагрузки K н_Р12 и K _{н Р}3 ₄;

• –    крутящий момент на входе редуктора Т ₁.

Внутри программы организованы три цикла:

– цикл «Цикл для S [ j ]» перебирает варианты сочетаний материалов, которые передаются из подпрограммы перебора сочетаний материалов;

– цикл «Цикл для ψ _ba = 0,1…0,4» перебирает значения параметра в указанном диапазоне с шагом 0,01;

– цикл «Цикл для ψ _bRe = 0,25…0,35» перебирает значения параметра в указанном диапазоне с шагом 0,01.

Далее все значения параметров подставляются в формулу (6) для вычисления оптимального значения передаточного отношения i ₃₄, которое проверяется по критериям, указанным в блоке сравнения.

Если i ₃₄ удовлетворяет этим критериям, то проводятся расчеты L (по формуле (5)), H , B , A_{w 34}, d_{e 2}, d_{w 4}. Из этих расчетов формируется массив, из которого выбираются и выводятся на экран оптимальные варианты по длине редуктора L и объему его внутренней полости V .

Если i ₃₄ не удовлетворяет критериям, то программа переходит к следующему шагу.

Анализ рассчитанных вариантов редукторов позволяет выбрать наиболее оптимальные значения параметров обеих ступеней.

На кафедре прикладной механики Сибирского государственного технологического университета помимо методики, приведенной выше, разработаны методики по расчету оптимальных конструкций цилиндрических двухступенчатых и планетарных редукторов. По данным методикам разработано программное обеспечение, используя которое, можно провести анализ конструкций всех перечисленных выше редукторов при одинаковых входных параметрах, и выбрать наиболее оптимальные конструкции как по длине, так и по объему внутренней полости редуктора.

Приведем пример по выбору оптимальной схемы для редуктора при заданных входных параметрах.

Зададим входные параметры для проведения расчета (табл. 1): i _общ – общее передаточное отношение редуктора; Т – момент на тихоходном валу редуктора, Н ⋅ м; Ма-териал/термообработка – материал и термообработка колес и шестерен редуктора; σ _н – допускаемое контактное напряжение зубьев колес и шестерен редуктора, Н ⋅ мм²; K _{н β} – коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев.

Введем эти параметры в программу и произведем расчет.

Варианты расчетов отсортируем по минимальной длине L _min и минимальному объему внутренней полости V _min редуктора и выведем в виде таблиц (табл. 2, 3 и 4).

Анализируя полученные данные, мы можем видеть, как произошла разбивка передаточного отношения между ступенями, ширину зубчатого венца первой и второй ступени и главное – геометрические размеры самого редуктора. В результате можно сделать вывод, что при входных параметрах, указанных в табл. 1, оптимальным по длине L и объему внутренней полости V будет планетарный четырехколесный редуктор с одним внешним и одним внутренним зацеплением.

Таким образом, представленное программное обеспечение позволяет с очень большой точностью определять оптимальную схему редуктора по длине и объему внутренней полости.

Входные параметры для расчета оптимальных конструкций редукторов

Таблица 1

i общ	Т , Н∙м	Материал/термообработка	σн, Н∙мм2	K нβ
20	940	45/ТВЧ	800	1,0

Параметры коническо-цилиндрического редуктора

Таблица 2

Тип редуктора	Материал/ термообработка колес и шестерен	σ н , Н∙м2	i 12	i 34	d e 2, мм	a w 34, мм	b 12, мм	b 34, мм	L , мм	B , мм	H , мм	V , мм 3
Коническо-цилиндрический ГТ-^1—"—I	45/ТВЧ	800	2,66	7,52	129,75	L min 169,56	30,93	67,82	449	128	335	19 253 120
	45/ТВЧ	800	2,51	7,95	134,44	V min 173,11	22,49	67,51	461	116	343	18 342 268

Таблица 3

Тип редуктора	Материал/ термообработка колес и шестерен	σ н , Н∙м2	i 12	i 34	a w 12, мм	a w 34, мм	Ψ ba12, мм	Ψ ba34, мм	L , мм	B , мм	H , мм	V , мм3
По развернутой схеме Я1—II--1^ Up______1 ч[ннн—^	45/ТВЧ	800	5,71	3,5	120,74	L min 152,39	0,28	0,392	410	–	–	9 087 719
	45/ТВЧ	800	5,15	3,89	161,41	V min 184,31	0,1	0,23	519	–	–	8 899 332
По соосной схеме Чн^ н1^—1—। '-У_Н—III—1	45/ТВЧ	800	7,25	2,76	148,65	L min –	0,22	0,396	388	–	–	9 291 183
	45/ТВЧ	800	4,87	4,11	157,05	V min –	0,1	0,38	414	–	–	8 125 736

Таблица 4

Тип редуктора							Материал/ термообработка колес и шестерен	σ н , Н∙м2	i 12	i 34	aw , мм	n k	m 12 / m 34	z 3 / z 2	Ψ ba 12 , мм	Ψ ba 34, мм	В , мм	L , мм	H , мм	V , 3 мм3
Трехколесный							45/ТВЧ	800	9	2,11	123,08	2	–	L min –	0,4	–	148	561	–	46 518 976
							45/ТВЧ	800	9	2,11	195,37	2	–	V min –	0,1	–	59	891	–	46 518 331
Четырехколесный с внешним зацеплением							45/ТВЧ	800	5	4,2	117,22	3	1,3	L min 0,3	0,1	0,387	57	430	–	10 556 617
							45/ТВЧ	800	5	4,2	117,22	3	1,3	V min 0,3	0,1	0,387	57	430	–	10 556 617
Четыр с одни и одни зацепл	ех м м ен	ко вн вн ие	лесны ешним утрен м			й 4 ним	45/ТВЧ	800	4,29	4,42	71,67	3	1,25	L min 0,45	0,35	0,395	53	260	–	3 597 430
							45/ТВЧ	800	4,41	4,31	110,16	3	1,35	V min 0,5	0,1	0,104	22	400	–	3 586 092
						1

K. Ya. Ivanov, N. I. Galibei

TWO-STAGE GEAR REDUCERS. THE CHOICE OF OPTIMAL SCHEME

The optimization of basic parameters of a right-angle parallel-shaft reducer and the choice of the optimal scheme of a two-stage gear reducer on the basis of calculation methods developed at the Department of Applied Mechanics of Siberian State Technological University are considered.

А. А. Назаров, М. Г. Носова

ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЕМОГРАФИЧЕСКИХ ПРОЦЕССОВ В ВИДЕ ПЯТИФАЗНОЙ СИСТЕМЫМАССОВОГО ОБСЛУЖИВАНИЯ*

Предложена математическая модель процесса изменения демографической ситуации в виде пятифазной автономной системы массового обслуживания с неограниченным числом приборов. Ее исследование выполнено методом моментов. Найдены первые и вторые моменты числа заявок, обслуживаемых в системе. Разработанная модель и метод применяются к прогнозированию процесса изменения демографической ситуации в Российской Федерации.

Параметры цилиндрического двухступенчатого редуктора по развернутой и соосной схемам

Параметры планетарных редукторов

В последние годы в результате экономических и политических изменений в нашей стране возросла потребность в построении научно обоснованных демографических прогнозов. Одним из методов демографического прогнозирования является разработка и исследование математических моделей, в частности применение моделей и методов теории массового обслуживания для моделирования демографических процессов.

В данной статье в качестве математической модели процесса изменения численности женского населения, например женщин Российской Федерации, рассматривается функционирование пятифазной автономной системы массового обслуживания (СМО) с неограниченным числом приборов.

Определим процесс функционирования такой СМО. Будем полагать, что продолжительность обслуживания ф каждой заявки складывается из пяти фаз:

Т = Т 1 + Т 2 + Т 3 + Т 4 + Т 5 .

Здесь все т. - независимые и экспоненциально распределенные случайные величины с параметрами ц , характеризующими продолжительности фаз обслуживания, = 1...5.

Поскольку интенсивность рождаемости существенно зависит от возраста женщин, то целесообразно рассматривать b(t) – интенсивность репродукции как функцию, зависимую от возраста женщины. Для указания такой зависимости рассмотрим систему, в которой три фазы соответствуют различным этапам репродуктивного возраста женщин.

Будем считать, что для заявок, находящихся на обслуживании, на второй, третьей и четвертой фазах возможно генерирование новых требований. Интенсивности генерирования новых заявок равны соответственно b2(t), b3(t) и b4(t). Интенсивности репродукции на первой и пятой фазах будем считать равными нулю, т. е. b1(t) = 0, b5(t) = 0. Поскольку случайные величины т , распределены экспоненциально, то средняя продолжительность -й фазы составляет 1/ц, i = 1...5. Тогда интенсивность репродукции на -й фазе запишем в виде b,( t) = 0,488bi (t )ц, где b (t) – суммарный коэффициент рождаемости в момент t [1]; 0,488 – вероятность рождения девочки;

= 1...5. Обслуживание каждой новой заявки начинается на первой фазе. Заявка, завершив обслуживание на -й фазе, с вероятностью r переходит к обслуживанию на + 1-ю фазу, а с вероятностью 1 – r завершает свое обслуживание и покидает систему, = 1...4. С вероятностью 1 после пятой фазы завершается полное обслуживание заявки.

Поскольку в рассматриваемой системе массового обслуживания отсутствует внешний источник заявок, так