0/1 Knapsack Problem using Diversity based Dual Population Genetic Algorithm

Genetic Algorithm (GA) is an optimization algorithm simpler than Calculus based optimization techniques and Dynamic Programming (DP) in implementation. It is used for solving problems in the area of industrial design by parameterization, Scheduling, Time Series Prediction, Single Machine Maximum Lateness Problem etc. [2]. But the problem associated with GA is that it is a population based algorithm and as the populations evolve, they lose diversity and their individuals are trapped in local optima, especially when involving complex problems which have a lot of peaks in the fitness landscape [3].

GA is a stochastic optimization tool, it is a non-deterministic process. Therefore solution evolved using GA may or may not be optimized i.e. it doesn’t ensure an optimal solution every time. This is called as premature convergence problem.

One of the solutions to premature convergence [4], [5] problem is population diversity based algorithm called Dual Population Genetic Algorithm (DPGA) [3], [6], [7], [18]. DPGA is a special type of GA where the two populations are generated viz. Main population and reserved population. The main population evolves similarly as to normal GA but reserve population has a special fitness function to provide diversity to the main population. Due to which all the search space is traversed and explored more effectively. This provides additional diversity to the main population. The information exchange between populations takes place through inter population crossbreeding. This technique helps to solve the problem of premature convergence [3], [6], [7].

0-1 knapsack problem (KP) is non deterministic polynomial (NP) problem. For NP problems, there are no precise and guaranteed algorithms that can run in polynomial time. Still it’s possible to generate a solution and check it in polynomial time by predicting or guessing the solution. GAs can be used to solve the larger NP problem efficiently. GAs produce the possible solution set by approximation and randomization and try to find out the optimal solution which nearer to the exact solution in polynomial time.

This paper explains how DPGA is implemented for solving 0/1 Knapsack Problem. Section II contains a literature survey of how the GA is applied on 0/1 knapsack problem. Section III explains the DPGA and implementation procedure. Section IV explains how we implement 0/1 knapsack using DPGA. Section V gives the implementation details. Section VI comprises results and discussion. Finally, Section VII concludes the paper on the basis of results and statistical analysis.

• II.    Literature Review

  Gordon and WimBOhm et.al. (1994) [8] proposed a note on the performance of GAs for Zero-One Knapsack Problems. In case of large problems branch-and-bound and depth-first methods outperform the GAs for finding optimal solutions and approximate solutions quickly. The results show the requirement for improved understanding of which problems are suitable for GAs and which problems are not.

Khuri, Back and Heitkotter (1994) [9] proposed the implementation of the 0/1 Multiple Knapsack Problem and GAs. In this work, GA allows for breeding and participation of infeasible strings in the population and allows in feasible breed strings to participate in the search as they do contribute information. Rather than augmenting the GA with domain-specific knowledge, introduced a fitness function with graded penalty term.

Sakawa and Kato (2002) [10] proposed GAs with double strings for 0/1 knapsack problem are first revisited together with some modifications and computational experiments. Then the GAs with double strings for 0/1 knapsack problems are extended to deal with more general 0/1 programming problems involving both positive and negative coefficients in the constraints. Especially, new decoding algorithms for double strings using reference solutions both without and with the reference solution updating procedure are proposed so that each of individuals is decoded to the corresponding feasible solution for the general 0/1 programming problems. The efficiency and effectiveness of the proposed methods are investigated by comparing them with a branch and bound method with respect to the accuracy of an approximate solution and the processing time through a number of numerical experiments.

Hristakeva and Shrestha (2004) [11] applied GA to solve 0/1 KP problem. In the experimentation two selection methods, roulette-wheel and group selection improves the results quality with the elitism.

Julstrom (2005) [12] proposed greedy, genetic, and greedy GAs for the quadratic knapsack problem. The quadratic knapsack problem alters the traditional knapsack problem by assigning values to individual objects and to the pairs of objects. These results illustrate the power of evolutionary algorithms augmented with heuristic strategies to achieve good results on combinatorial problems.

Lin (2006) [13] experimented the KP with imprecise weight coefficients using GAs. Proposed approach simulates a fuzzy number by distributing it into some partition points. This work concluded that proposed fuzzy GA approach is different, and gives better results than the traditional fuzzy approach.

Shi (2006) [14] proposed the improved Ant Colony Algorithm (ACO) for 0/1 KP.

JoãoAlvesa, Almeidab (2007) [15] proposed a multi objective Tchebycheff based GA (MOTGA) for the multidimensional knapsack problem. This paper presented a new multi objective GA based on the Tchebycheff scalarizing function, which aims to generate a good approximation of the non dominated solution set of the multi objective problem. Computational results are presented and compared with the outcomes of other evolutionary algorithms. The number of potentially non dominated solutions obtained for each instance was not very high (namely when compared with MOGLS), but the solutions seem to be well dispersed and show good quality indicators.

Rohlfshagenand, Bullinaria (2007) [16] implemented an improved Exonic GA (ExGA II) for the Multiple Knapsack Problem. The algorithm’s overall performance indicates good scaling properties, although further testing on larger problem sets is required to fully validate this claim.

Zhao, Man, Qi (2008) [17] proposed CGS-MSM PGA based on Multi-Agent and its application in solving 0-1 Knapsack Problem. After testing the algorithm through the simulation testing results show that the computational speed and precision are better than the traditional GA and the original CGS-MSM PGA.

Mohanty and Satapathy (2009) [18] proposed an evolutionary multi objective GA to solve 0/1 Knapsack Problem. Few numerical experiments are realized using the best and recent algorithm in this paper. In this paper, few numerical experiments are realized using the best and recent algorithm. The results show that the new proposed algorithm performs better than the existing evolutionary approach to this problem.

Zhao and Huang (2009) [19] implemented GA based on greedy strategy in the 0/1 Knapsack Problem. In this paper, based on 0/1 knapsack problem is given a mathematical model, and analysis of the greedy strategy. Given a GA to solve the knapsack problem, greedy strategy combining the traditional GA has been improved and shortened the time to solve, and to improve the accuracy of the solution. The improvement of this GA lies in the establishment of the original population, to use of greedy strategy solution as the original code of the algorithm.

Ahmed and Younas (2011) [20] proposed dynamic programming based GA to solve Multiple Knapsack Problems (MKP) problem. Proposed GA achieves the optimal solution and reduced the computation time.

Singh (2011) [21] applied the GA to solve the specific 0/1 KP problem and experimented various selection method of GA.

Tuo, Yong, and Deng (2014) [22] proposed harmony search algorithm based on teaching-learning strategies (HSTL) for 0-1 KP.

Many researchers solved the 0/1 KP by various methods with improvements in method or experimentation of variation in operators of method or comparing the performance operators of methods to solve KP. Most researchers’ interest is in solving the KP problems with the new method or some improvements in the algorithm rather than improving the performance of solving KP. The solution of KP by various methods should be compared with respect to efficiency, efficacy and success rate.

• III.    Dual Population Genetic Algorithm

DPGA can be viewed as type of multi population GA in that it manipulates two isolated populations, but can also be considered a memory based algorithm because the additional population only plays the role of a repository for maintaining diversity or additional information [23].

For the main population to exploit the diversity preserved in the reserve population there must be means to exchange information between the populations. An individual of one population of a DPGA is unlikely to survive in the other because it gets contradictory fitness evaluations in different populations. A good individual in the main population, for example, may not look good in the reserve population because it does not contribute much to diversity. Therefore, DPGAs use interpopulation crossbreeding as a means of information exchange.

DPGA starts with two randomly generated populations. The individuals of each population are evaluated by its own fitness function based on its evolutionary objective. The evolution of each population and the communication between populations is performed by inbreeding between parents from the same population, crossbreeding between parents from different populations, and survival selection among these offspring [24]. Fitness functions for the reserve and main populations, procedure of reproduction and survival selection for both the populations are described as follows.

• A.    Fitness Function for Main Population

The main populations and reserve population of DPGA have different evolutionary objectives. Therefore they use different fitness functions. The fitness function fm of the main population is the objective function of the given problem because its objective is to find a good solution to the given problem.

• B.    Fitness Function for Reserve Population

Equation (1) is the fitness function of the reserve population, which gives a high fitness value to an individual to maintain an appropriate distance to the individuals in the main population thereby providing diversity to the main population.

frδ(x)=1-|δ-d(M,x)| (1)

Where,

d(M, x) : average distance (0 ≤ d(M, x) ≤ 1) between the main population M and individual x of the reserve population.

δ : desired distance (0 ≤ δ ≤ 1) between two population.

Assuming a binary representation for a chromosome d(M, x) is calculated using equation (2) [23,24, 25].

• C.    DPGA Algorithm

DPGA [18, 19] steps for production of new generations are given in figure 1.

d(M,x) =  1  ∑ hd(m, x)|M |m∈M

1l=∑|fM,k -xk | l k=1

Where, mi: ith chromosome of the main population.

hd(m_i, x) : Hamming distance between two chromosome vectors m and x.

l : length of chromosome.

mi, k : kth gene on chromosome mi and xk fM,k : frequency of the kth gene value ‘1’ of the main population M.

• x i : frequency of k ^th gene value ‘1’ of the chromosome vector x and is identical to the k ^th gene value of the chromosome.

• IV. Knapsack Problem

Knapsack problem is a constraint optimization problem. In this problem, a number of items n are provided. A knapsack with a certain capacity or volume V is provided. Each object i has a specific positive integer volume V_i and a positive integer benefit B i . Also there are Q i copies of the object i such that 0 ≤ Q i ≤ ∞ available. In the knapsack problem, a combination of these items is to be selected so as to maximize the benefit but within the capacity of the sack.

Procedure DPGA

Begin

Initialize main population M 0 and R 0

Evaluate M 0 using f m (x)

Evaluate R 0 using f r (x)

t:= 0

Repeat

Repeat

Step I: Parent Selection:

• 1.    Select two parent p m1 and p m2 from M t

• 2.    Select two parent p r1 and p r2 from R t

Step II: Offspring generation:

• 1.    (Inbreeding) Generate two offspring c m1 and c m2 by recombining p m1 and p m2

• 2.    (Inbreeding) Generate two offspring c r1 and c_r2 by recombining p_r1 and p_r2

• 3.    (Crossbreeding) Generate two offspring c c1 and c c2 by recombining p m2 and p r1

• 4.    Mutate all generated offspring

• 1.    Evaluate c m1 , c m2 c c1 and c c2 i.e.O M using f m (x) and add the best two to M t+1

• 2.    Evaluate c r1 , c r2 , c c1 and c c2 i.e.O R using f_r(x) and add the best two to R_t+1

Until |M_t+1| = = pop_size t:= t+ 1

Until terminated = true // e.g., t > t max

End

Where,

M t and R t are main and reserve populations respectively.

• p_m1 and p_m2 are selected parents from main population.

• p r1 and p r2 are selected parents from reserve population.

• c m1 and c m2 are child’s of main population inbreeding.

• c c1 and c c1 are child’s of crossbreeding.

• c r1 and c r1 are child’s of reserve population inbreeding.

M t+1 and R t+1 are next generation main and reserve populations respectively.

Fig. 1. Pseudo code of DPGA [24]

Let X i determine the number of copies of an object i to be placed in the knapsack. And the objective function is to-

Maximize Benefit:

n

∑ ^Bi ^Xi ^;

i = 0

Subject To Constraints:

n

L 1 X 5 V i=0

• V. Implementation details of 0-1 KP using for GAS

• A.    Representation of the knapsack items

Array is used as a data structure, to store benefits and volumes of items separately, as shown below:

Volumes:

1	2	3	4	5
10	20	30	40	50
Benefits: 1      2		3	4	5
5	10	15	20	25

The above diagram shows that item no. 1 has 10 as the volume and 5 as its benefit. Similarly, item no. 2 has 20 as its volume and 10 as its benefit and so on.

• B.    Encoding of the chromosomes for knapsack problem

An array is represented as a chromosome, having a size equal to the number of items in the sack (for example size is 5). Each element of an array denotes that whether an item is included in the sack means ‘1’ or not in sack means ‘0'. For example, the following chromosome indicates that the 1st, 2nd and 4th item is included in the knapsack.

Encoding:

1     2        3        4        5

1      1         0         1         0

A three-dimensional array (chromosomes [Size] [number of items] is used to represent the whole population of chromosomes). Size means the number of chromosomes in a population. The second dimension of an array represents the number of items that may good to be included in the knapsack. The third dimension of an array is used to represent the total volume and benefits of that chromosome. The data structure representation is same as it is in [2].

• C.    Termination conditions used

The GA terminates at completion of the number of generations.

• D.    Fitness calculation

Fitness calculation of each chromosome is done by summation of the benefits of the items that are added in the knapsack; with making sure that the capacity of the knapsack is not exceeded. To check the validity solution, we check the volume of the chromosome is lesser than the capacity of the knapsack, if not then one of the bits in the chromosome whose value is ‘1’ is inverted and the chromosome is checked again [1].

• E.    Selection method used

In the GA evolution process, we used the elitism in which the two of the fittest chromosomes are copied as it to the next population, so the best solutions found in old population will not be lost.

• F.    Crossover method used

One point crossover is used to evolve the population. Crossover probability is 80%.

• G.    Mutation method used

The mutation probability in this work 20% of the population. Mutation method used is one bit mutation.

• VI.   Results and Discussion

DPGA for constrained optimization problems is experimented on Intel Core-i3 processor system with Windows-7 as an operating system. The source code is developed in Java. The experiments are conducted on 0/1 knapsack problem data sets. First data set is generated randomly for experimentation and called as the random data set. Second and third data sets are standard data sets taken from the standard resource.

• A.    Random Data Set (Data set 1)

Results are taken using random data set. Random data is generated on our above specified machine. Random data set is generated using a random number generator. These randomly generated numbers include weight and benefit of every object. This data set is input to the algorithm. Data set 1 are used to compare performance of SGA with DPGA.

Weights = {14, 29, 13, 36, 15, 19, 33, 36, 13, 36, 36, 31, 43, 26, 16, 16, 23, 30, 24, 27}

Benefits = {19, 19, 11, 11, 11, 4, 11, 15, 18, 14, 2, 15, 9, 14, 9, 3, 7, 14, 8, 6}

• B.    Standard Data Set (Data set 2)

The standard data set 2 are taken from [26] for experimentation of 0/1 knapsack problem. Data set 2 are used to compare performance of SGA with DPGA.

Weights=

{135,139,149,150,156,163,173,184,192,201,210,214,221, 229,240}

Benefits={70,73,77,80,82,87,90,94,98,106,110,113,11 5,118,120}

• C.    Standard Data Set (Data set 3)

Standard data set 3 are taken from github [27] for experimentation of 0/1 knapsack problem. This data set 3 are used to compare performance of SGA with DPGA.

Weights = {56, 59, 80, 64, 75, 17}

Benefits = {50, 50, 64, 46, 50, 5}

Table 1. Parameter Settings and Results for Random Data SET1

Parameter Settings for Random Data
Dimension	20		Population Size	20
		Capacity
		400
Standard Benefit	200		Generation No.	50
Knapsack Benefit and Generation No.
Sr. No	SGA Gen. No.	SGA Benefit	DPGA Gen. No.	DPGA Benefit
1	28	179	20	200
2	50	200	34	200
3	45	197	43	197
4	22	197	22	197
5	49	187	30	187
6	33	198	33	198
7	44	190	32	190
8	50	192	29	192
9	46	193	21	193
10	38	198	38	198
Statistical Analysis
Benefit	SGA		DPGA
Mean	193.10		195.20
SD	6.4368		4.4422
SEM	2.0355		1.4047

Table 2. Parameter Settings and Results for Standard data set 2

Parameter Settings for Standard Data
Dimension	15			Population Size	20
			Capacity
			750
Standard Benefit	395			Generation No.	50
Knapsack Benefit and Generation No.
Sr. No	SGA Gen. No.		SGA Benefit	DPGA Gen. No.	DPGA Benefit
1	63		395	83	395
2	95		395	181	394
3	127		395	152	394
4	54		394	2	395
5	15		395	1	395
6	12		395	46	394
7	51		395	37	394
8	46		393	19	395
9	49		395	5	395
10	42		395	15	395
Statistical Analysis
Benefit		SGA		DPGA
Mean		394.70		396.60
SD		0.6749		0.5163
SEM		0.1509		0.1154

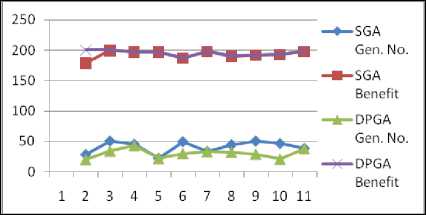
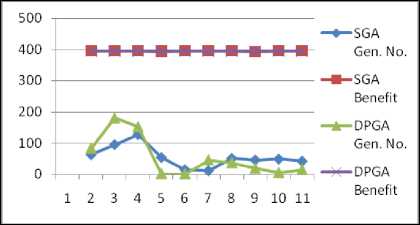
Table 3. Parameter Settings and Results for Git data set 3

Parameter Settings for Git Data
Dimension	6	Capacity 190	Population Size		10
Standard Benefit	150		Generation No.		20
Knapsack Benefit and Generation No.
Sr. No	SGA Gen. No.	SGA Benefit	DPGA Gen. No.		DPGA Benefit
1	1	119	4		150
2	1	150	1		150
3	1	150	8		150
4	10	150	1		146
5	1	119	5		150
6	19	146	1		150
7	2	150	1		150
8	2	150	1		150
9	16	146	1		150
10	15	146	1		150
Statistical Analysis
Benefit	SGA			DPGA
Mean	142.60			396.60
SD	12.5715			1.2649
SEM	3.9754			0.4000

Table 4. Comparison of SGA and DPGA based on mean, standard deviation and standard error of mean for data sets.

	Data set 1		Data set 2		Data set 3
Benefit	SGA	DPGA	SGA	DPGA	SGA	DPGA
M	193.1	195.2	394.7	396.6	142.6	396.6
SD	6.4	4.4	0.67	0.51	12.5	1.2
SEM	2.0	1.4	0.15	0.11	3.9	0.40

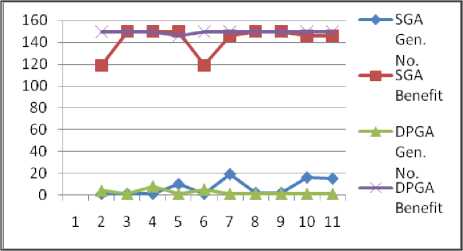
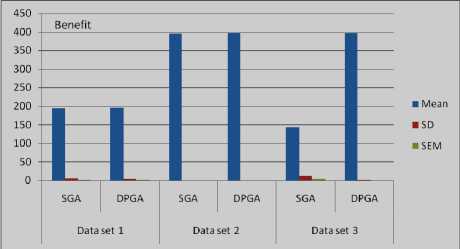
Fig. 5. Comparison of SGA and DPGA based on mean, standard deviation and standard error of mean for data sets.

Table IV shows the comparison of mean (M), standard deviation (SD) and standard error of mean (SEM). Values obtained for SD and SEM decrease in case of DPGA with the comparison to SGA for the knapsack problem. Figure 5 shows the comparison of benefit given by SGA and DPGA based on mean, standard deviation and standard error of mean for data sets

From the experimental results, it is observed that the mean value obtained for knapsack benefit using DPGA is significantly better over the mean value obtained using SGA.

• VII.    Conclusion

This paper presents a novel approach to solve 0/1 knapsack problem using DPGA. DPGA provides a solution to problems like premature convergence and population diversity of SGA. Experimental results show that DPGA solves the 0/1 knapsack problem effectively than SGA. The additional population of DPGA provides population diversity by using the additional fitness function. Benefits achieved by 0/1 knapsack problem are in lesser effort (function evaluation), with better efficacy (mean, standard deviation) and standard error of mean.

In future, the DPGA can also be checked for more complex knapsack problems. Further, DPGA can be improved for efficiency, efficacy and success rate by adding more reserve population to DPGA. A performance comparison of DPGA could be done with other metaheuristics.

Acknowledgment

The authors are thankful to the anonymous reviewers as well as the editors for their valuable comments and suggestions which have led to improve the quality of presentation of the paper. Our special thanks to T. Park, R. Choe and K.R. Ryu for their work on Dual Population Genetic Algorithm published in various journals and conferences.