3D Face Recognition based on Radon Transform, PCA, LDA using KNN and SVM

Biometrics (or biometric authentication) refers to the identification of humans by their characteristics or traits. Biometrics is used in computer science as a form of identification and access control. It is also used to identify individuals in groups that are under surveillance. Biometric identifiers are the distinctive, measurable characteristics used to label and describe individuals. Biometric identifiers are often categorized as physiological versus behavioral characteristics. Physiological characteristics are related to the shape of the body. Examples include, but are not limited to fingerprint, face recognition, DNA, Palm print, hand geometry, iris recognition, retina and odour/scent. Behavioral characteristics are related to the pattern of behavior of a person, including but not limited to: typing rhythm, gait, and voice. Some researchers have coined the term behaviometrics to describe the latter class of biometrics.

More traditional means of access control include token based identification systems, such as a driver's license or passport, and knowledge based identification systems, such as a password or personal identification number. Since biometric identifiers are unique to individuals, they are more reliable in verifying identity than token and knowledge based methods; however, the collection of biometric identifiers raises privacy concerns about the ultimate use of this information.

Human face images are useful not only for person recognition, but for also revealing other attributes like gender, age, ethnicity, and emotional state of a person. Therefore, face is an important biometric identifier in the law enforcement and human computer interaction (HCI) communities. Detecting faces in a given image and recognizing persons based on their face images are classical object recognition problems that have received extensive attention in the computer vision literature. While humans are perceived to be good at recognizing familiar faces, the exact cognitive processes involved in this activity are not well understood. Therefore, training a machine to recognize faces as humans do is an arduous task. However, general methods used in object recognition such as appearance based, model based, and texture based approaches are also applicable to the specific problem of face detection and recognition.

The face is the frontal portion of the human head, extending from the forehead to the chin and includes the mouth, nose, cheeks, and eyes. Being the foremost part in one’s interactions with the outer world, the face houses most of the fundamental sensory organs necessary for perceiving the world around, namely, eyes for seeing, nose for smelling, mouth for tasting, and ears for hearing. The face is considered to be the most commonly used biometric trait by humans; we recognize each other and, in many cases, establish our identities based on faces. Hence, it has become a standard practice to incorporate face photographs in various tokens of authentication such as ID cards, passports, and driver’s licenses.

Face Recognition and verification have been at the top of the research agenda of the computer vision community for more than a decade. The scientific interest in this research topic has been motivated by several factors. The main attractor is the inherent challenge that the problem of face image processing, face detection and recognition. However, the impetus for better understanding of the issues raised by automatic face recognition is also fuelled by the immense commercial significance that robust and reliable face recognition technology would entail. Its applications are envisaged in physical and logical access control, security, man-machine interfaces and low bitrate communication.

To date, most of the research efforts, as well as commercial developments, have focused on two dimensional (2D) approaches. This focus on monocular imaging has partly been motivated by costs but to a certain extent also by the need to retrieve faces from existing 2D image and video database. With recent advances in image capture techniques and devices, various types of face-image data have been utilized and various algorithms have been developed for each type of image data. Among various types of face images, a 2D intensity image has been the most popular and common image data used for face recognition because it is easy to acquire and utilize. It, however, has the intrinsic problem that it is vulnerable to the change of illumination. Sometimes the change of illumination gives more difference than the change of people, which severely degrades the recognition performance. Therefore, illumination-controlled images are required to avoid such an undesirable situation when 2D intensity images are used. To overcome the limitation of 2D intensity images, Three Dimensional (3D) images are being used, such as 3D meshes and range images. A 3D mesh image is the best 2D representation of 3D objects. It contains 3D structural information of the surface as well as the intensity information of each point. By utilizing the 3D structural information, the problem of vulnerability to the change of illumination can be solved. A 3D mesh image is suitable image data for face recognition, but it is complex and difficult to handle.

A range image is simply an image with depth information. In other words, a range image is an array of numbers where the numbers quantify the distances from the focal plane of the sensor to the surfaces of objects within the field of view along rays emanating from a regularly spaced grid. Range images have some advantages over 2D intensity images and 3D mesh images. First, range images are robust to the change of illumination and color because the value on each point represents the depth value which does not depend on illumination or color. Also, range images are simple representations of 3D information. The 3D information in 3D mesh images is useful in face recognition, but it is difficult to handle. Different from 3D mesh images, it is easy to utilize the 3D information of range images because the 3D information of each point is explicit on a regularly spaced grid. Due to these advantages, range images are very promising in face recognition.

The majority of the 3D face recognition studies have focused on developing holistic statistical techniques based on the appearance of face range images or on techniques that employ 3D surface matching. A survey of literature on the research work focusing on various potential problems and challenges in the 3D face recognition can be found in the survey [1-5]. Gupta et al.[6] presented a novel anthropometric 3D face recognition algorithm. This approach employs 3D Euclidean and Geodesic distances between 10 automatically located anthropometric facial fiducial points and a linear discriminant classifier with 96.8% recognition rate. Lu et al. [7] constructed many 3D models as registered templates, then they matched 2.5D images (original 3D data) to these models using iterative closest point (ICP). Chang et al. [8] describe a “multiregion” approach to 3D face recognition. It is a type of classifier ensemble approach in which multiple overlapping sub regions around the nose are independently matched using ICP and the results of the 3D matching are fused. Jahanbim et al. [9] presented an approach of verification system based on Gabor features extracted from range images. In this approach, multiple landmarks (fiducials) on face are automatically detected, and also the Gabor features on all fiducials are concatenated, to form a feature vector to collect all the face features. Hiremath et al.[18] have discussed the 3D face recognition by using Radon Transform and PCA with recognition accuracy of 95.30%. Hengliand Tang et al.[19] presented a 3D face recognition algorithm based on sparse representation. In this method they used geometrical features, namely, triangle area, triangle normal and geodesic distance.

In this proposed method, our objective is to propose Discriminant Analysis method for face recognition based on Radon Transformation, Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA) which are applied on 3D face images. The experimentation is carried out using three publicly available databases, namely, Bhosphorus, Texas and CASIA 3D face databases. The rest of this paper is organized as follows. Section 2 describes materials and methods used for proposed method. Section 3 gives details of the training and testing algorithms based on Linear Discriminant Analysis. The experimental results and discussion is described in Section 4. Section 5 Concludes the paper.

• II.    Materials and methods

For purpose of experimentation of the proposed methodology, the face images drawn from the following 3D face databases are considered: (i) Boshphorus 3D face database, (ii) Texas 3D face database, (iii) CASIA 3D face database.

• A.    Bosphorus 3D Face Database

The Bosphorus 3D face database consists of 105 subjects in various poses, expressions and occlusion conditions. The 18 subjects have beard/moustache and the 15 subjects have hair. The majority of the subjects are aged between 25 and 35. There are 60 men and 45 women in total, and most of the subjects are Caucasian. Two types of expressions have been considered in the Bosphorus database. In the first set, the expressions are based on action units. In the second set, facial expressions corresponding to certain emotional expressions are collected. These are: happiness, surprise, fear, sadness, anger and disgust.

• B.    Texas 3D Face Database

  The Texas 3D Face Recognition (Texas 3DFR) database is a collection of 1149 pairs of facial color and range images of 105 adult human subjects. These images were acquired using a stereo imaging system manufactured by 3Q Technologies (Atlanta, GA) at a very high spatial resolution of 0.32 mm along the x, y, and z dimensions. During each acquisition, the color and range images were captured simultaneously and thus the two are perfectly registered to each other. This large database of two 2D and 3D facial models was acquired at the company Advanced Digital Imaging Research (ADIR), LLC (Friendswood, TX), formerly a subsidiary of Iris International, Inc. (Chatsworth, CA), with assistance from research students and faculty from the Laboratory for Image and Video Engineering (LIVE) at The University of Texas at Austin. This project was sponsored by the Advanced Technology Program of the National Institute of Standards and Technology (NIST). Texas 3DFRD was created to develop and test 3D face recognition algorithms intended to operate in environments with cooperative subjects, wherein, the faces are imaged in a relatively fixed position and distance from the camera [11].

• C.    CASIA 3D Face Database

  CASIA 3D Face Database consisting of 4624 scans of 123 persons using the non-contact 3D digitizer, Minolta Vivid 910. During building the database, not only the single variations of poses, but also expressions and illuminations are considered [12].

• III.    Proposed method

• A.    Radon Transform

The Radon Transform (RT) is a fundamental tool in many areas. The 3D radon Transform is defined using 1D projections of a 3D object f(x,y,z) where these projections are obtained by integrating f(x,y,z) on a plane, whose orientation can be described by a unit vector α . Geometrically, the continuous 3D Radon transform maps a function R³ into the set of its plane integrals in R. Given a 3D function f ( x ) f ( x , y , z ) and a plane whose representation is given using the normal α and the distance s of the plane from the origin, the 3D continous Radon Transform of f for this plane is defined by

∞∞∞

ℜf (a,s) = ∫∫∫f (x)δ(xTα-s)dx

-∞ -∞ -∞

∞∞∞f (x, y,z)δ(xsinθcosφ+ ysinθsinφ+zcosθ-s)dxdydz -∞ -∞ -∞ where x =[x,y,z]T, α =[ sinθcosφ, sinθsinφ, cosθ ]T, and δ is Dirac’s delta function defined by δ(x) =0, x≠0, ∞

∫ δ(x)dx = 1 . The Radon transform maps the spatial -∞ domain (x,y,z) to the domain (α,s )[13].

• B.    Linear Discriminant Analysis

The principal component analysis (PCA) is a standard technique used to approximate the original data with lower dimensional feature vectors [14-16]. The basic approach is to compute the eigenvectors of the covariance matrix, and approximate the original data by a linear combination of the leading eigenvectors. The mean square error (MSE) in reconstruction is equal to the sum of the remaining eigenvalues. The coefficients of projection of an arbitrary data vector along the principal components (eigenvectors) form the feature vector. In PCA, since no class membership information is used, the data vectors of the same class and of different classes are treated similarly. In the linear discriminant analysis

(LDA), the class membership information is used to emphasize the variation of data vectors belonging to different classes and to deemphasize the variations of data vectors within a class. The LDA produces an optimal linear discriminant function f ( x ) = W^Tx which maps the input into the classification space in which the class identification of this sample is decided based on some metric such as Euclidian distance [14-16]. A typical LDA implementation is carried out via scatter matrices analysis. The within and between-class scatter matrices as follows:

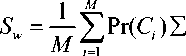
S b = "1 X Pr( C i )( m i - m )( m i — ^m ) ^T

M i = 1                                   (3)

Here Sw is the within-class scatter matrix showing the average scatter X, of the sample vectors x of different class C around their respective mean m :

Xi = E[(x — mi-)(x — mJ T C = Ci- ]     (4)

Similarly, S is the between-class scatter matrix, representing the deviation of the conditional mean vectors m i ’s from the overall mean vector m. Various measures are available for quantifying the discriminatory power, the commonly used one being,

J ⁽ w ) =

w^TS_ww w^TS_bw ^,

where w is the optimal discrimination projection and can be obtained via solving the generalized eigenvalues problem S_bw = A S_wW . The distance measure used in the matching could be a simple Euclidian distance. Thus, the fundamental difference between the PCA and LDA approaches is that, while PCA performs eigenvalues analysis and covariance matrix, the LDA does it on scatter matrices.

• C.    Proposed Methodology

The Radon transform is applied to an input 3D facial image I 1 in steps of h from 0^o to 180^o orientations, where h may be 1^o, 2^o, 3^o or any convenient value. It yields a binary image I 2 with facial area being segmented. After superposing I 2 and I 1 , the cropped facial range image I 3 is obtained. Next, the principal component analysis (PCA) technique is applied to the complete set of such cropped facial range images corresponding to the face images in the face database. It yields the set of Eigen faces. After yielding the Eigen faces we perform Linear Discriminant

Analysis (LDA) to these Eigen faces which are used for face recognition in a given test 3D face image. The Fig. 1 and 2 shows the overview of proposed framework and intermediate results of the Radon transformation of an input 3D face image respectively. The algorithms of the training phase and the testing phase of the proposed method are given below:

Algorithm 1: Training Phase

• 1.    Input the 3D face image I 1 from the training set containing M images (Fig.2(a)).

• 2.    Apply Radon transform, from 0^o to 180^o orientations (in steps of h ), to the input range image I 1 yielding a binary image I 2 (Fig.2(c)).

• 3.    Superpose the binary image I 2 obtained in the Step 2 on the input range image I₁ to obtain the cropped facial range image I₃ (Fig.2 (d)).

• 4.    Repeat the Steps 1 to 3 for all the M facial range images in the training set.

• 5.    Apply PCA to the set of cropped facial range images obtained in the Step 4 and obtain M Eigen faces.

• 6.    Compute the weights w , w , ..., w for each training face image, where p < M is the dimension of Eigen subspace on which the training face image is projected.

• 7.    Store the weights w , w ,..., w for each training image as its facial features in the PCA feature library of the face database.

• 8.    Perform LDA on the feature subspace (i.e., weight vectors).

• 9.    Store the LDA components (feature vectors) in the LDA feature library of the face database.

Algorithm 2: Testing Phase

• 1.    Input the test 3D face image Z₁.

• 2.    Apply Radon transform, from 0^o to 180^o orientations (in steps of h), to the input range image Z 1 yielding a binary image Z 2 .

• 3.    Superimpose the binary image Z 2 on Z 1 to obtain the cropped facial image Z 3 .

• 4.    Compute the weights w^ s , i = 1,2,..., p , for the test image Z 1 by projecting the test image on the LDA feature subspace of dimension p .

• 5.    Compute the Euclidian distance D between the feature vector w^test and the feature vectors stored in the LDA feature library.

• 6.    The face image in the face database, corresponding to the minimum distance D computed in the Step 5, is the recognized face.

• 7.    Output the texture face image corresponding to the recognized facial range image of the Step 6.

• IV.    Experimental results

The experimentation is carried out using three publicly available databases, namely, Bhosphorus, Texas and

CASIA 3D face databases. The proposed method is implemented using Intel Core 2 Quad processor @ 2.66 GHz machine and MATLAB 7.9. In the training phase, 2 frontal face images with neutral expression of each 100 subjects are selected as training data set. In the testing phase, randomly chosen 200 face images of the Bhosphorus, Texas and CASIA 3D face database with variations in facial expressions are used. The sample training images which are used for our experimentation are shown in the Fig.3, and their corresponding texture images are shown in the Fig.4. The Eigen faces and mean facial range image computed for PCA during the training phase are shown in the Fig.5 and 6, respectively. The classification is done using different classifiers, namely, minimum distance classifier, K-NN and SVM.

The comparison of recognition rates obtained by the proposed (RT+PCA+ LDA) approach, PCA (alone) and RT+PCA approach is presented in the Table 1. The projection orientation of Radon transform is in steps of 1o, 2o and 5o. We observe that the proposed method, namely, RT (with steps of 1o orientation) with PCA and LDA, yields better results as compared to the PCA (alone) and RT+PCA method.

The graph of recognition rates versus the number of Eigen faces is shown in the Fig.7 for the proposed method (RT+PCA+LDA) with other PCA and RT+PCA methods. It is observed that the recognition rate improves as the number of Eigen faces is increased. It is 99.20% for 40 Eigen faces in case of proposed method using SVM classifier. Further, the proposed method based on RT, PCA and LDA outperforms the PCA method. The Fig. 8 shows the receiver operating curve (ROC) space, defined by FAR versus FRR as x and y axes respectively, which depicts relative trade-offs between true positive and false positive for the proposed method implemented using three face databases, namely, Bhosphorus 3D face database, Texas 3D face database and CASIA 3D face database. It has yielded equal error rates (ERR) 15.3691, 13.0766 and 11.5310 respectively. We compare the rank-one recognition rates of the proposed method to the state-of-the-art 3D face recognition methods, namely, 3D face recognition using RT+PCA[18], LDA [8] and sparse representation [19] in the Table 2.

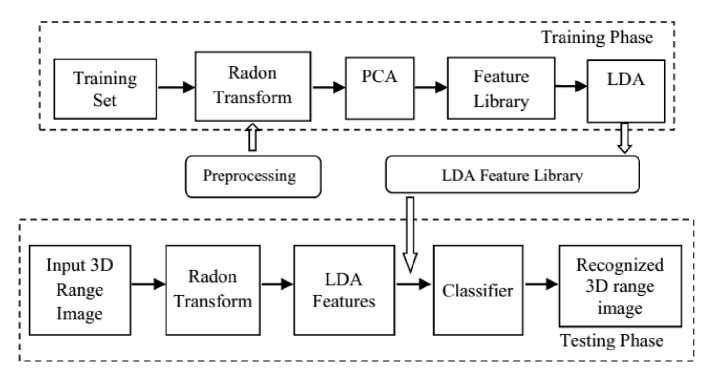
Fig. 1: Overview of proposed framework

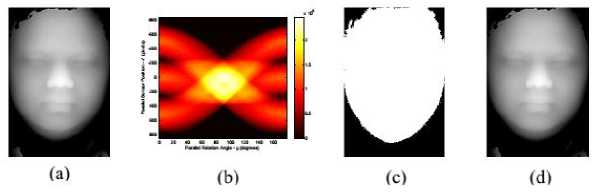
Fig. 2: (a) The range image I1, (b) Radon transform of I1 in 0oto 180o orientation, (c) Binary image I2 obtained after Radon transformation, (d) cropped facial range image I3 after superposing I2 and I1.

□□□□□

(a)                (b)              (c)                (d)                (e)

Fig. 3: Sample range images of the training set.

Fig. 4: The facial texture images corresponding to the training range images of the Fig.3

Fig. 5: The first five Eigen faces obtained by using the PCA in the training phase.

Fig. 6 : Mean facial range image computed in the Step 5 for PCA during the training phase.

Table 1. The face recognition accuracy(%) and recognition times (in Secs.) obtained by the proposed method using different number of eigen faces and LDA components.

No.of Eigen faces	PCA [18]		RT+PCA [18]		RT + PCA + LDA (Proposed Method)
	Accu racy %	Time (in secs.)	Accu racy %	Time (in secs.)	Recognition Accuracy			Average Time taken (in secs.)
					Minimum Distance Classifier	KNN (K=5)	SVM
5	58.5	9.813	60.1	9.941	61.16%	61.70	62.00%	9.992
10	76.1	9.822	77.5	9.950	77.90%	78.20%	79.50%	9.990
15	81.5	9.824	84.36	9.950	85.10%	85.50%	85.70%	9.970
20	87.1	9.828	90.19	9.953	91.20%	91.70%	91.70%	9.986
25	87.61	9.834	94.1	9.953	94.20%	94.50%	94.70%	9.992
30	88.5	9.845	94.16	9.953	95.91%	96.00%	96.00%	10.931
35	89.11	9.861	95.2	10.170	97.90%	97.90%	98.70%	10.981
40	89.47	10.161	95.3	10.172	99.16%	99.20%	99.20%	11.000

Table 2. Comparison of the proposed method with the state-of-the-art 3D face recognition algorithms.

Method	Recognition Accuracy	Dataset used
Proposed Method (RT+PCA+LDA with SVM)	99.20%	Texas 3D face database
Chang et. al., [8] (Gabor features around facial fiducial points)	96.80%	Texas 3D face database
Hiremath et.al., [18] 3D face recognition using RT+PCA	95.30%	Texas 3D face database
Tang et.al.,[19] Sparse Representation, (Triangular area/normal, Geodesic distance)	95.30%	BJUT-3D and FRGC v2

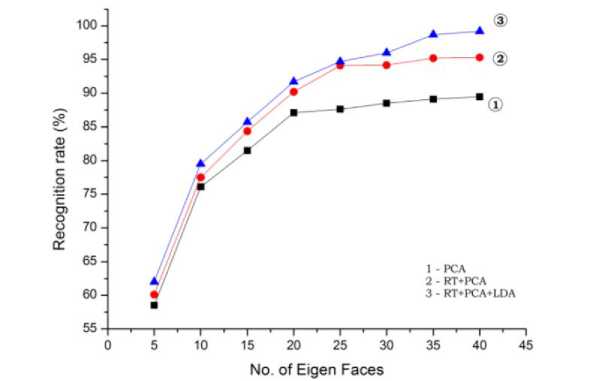
Fig. 7: The comparison of the recognition accuracy (%) versus the number of eigen faces for the proposed method (RT+PCA+LDA) with the methods in [18]

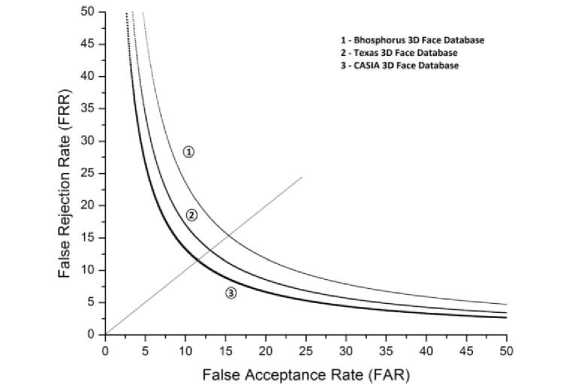
Fig. 8: Receiver operating characteristic (ROC) curves for the proposed method for Bhosphorus, Texas and CASIA 3D face databases with equal error rates 15.3691, 13.0766 and 11.5310, respectively

• V.    Conclusion

Face Recognition and verification have been at the top of the research agenda of the computer vision community for more than a decade. The scientific interest in this research topic has been motivated by several factors. The main attractor is the inherent challenge that the problem of face image processing, face detection and recognition. In this paper, we have proposed a novel hybrid method for Three Dimensional (3D) face recognition using Radon transform with PCA and LDA based features on face range images. In this method the LDA based feature computation can be done at high speeds, and recognition can be done in almost real time. Our experimental results yield 99.20% recognition performance with low complexity and a small number of features, which compares well with other state-of-the-art methods. The experimental results demonstrate the efficacy and the robustness of the method to illumination and pose variations. The recognition accuracy can be further improved by considering a larger training set and a better classifier.

Acknowledgment

The authors are grateful to the referees for their helpful comments and suggestions. Also, the authors are indebted to the University Grants Commission, New Delhi, for the financial support for this research work under UGC-MRP F.No.39-124/2010 (SR).